基于神经网络的部队投送路径优化方法研究

汪 欣, 王广东

(1.陆军军事交通学院学员五大队研究生队，天津 300161；2.陆军军事交通学院军事交通运输研究所，天津 300161)

现代战争凸显速度制胜，快速投送是决定战争胜负的关键因素。我军目前正在大力发展投送力量的建设，以提升部队全域机动、立体攻防的作战能力[1]。随着我国国家利益的拓展和战略投送能力的提高，部队投送范围逐渐由本土向跨区、跨境延伸，投送环境发生了巨大改变，日益呈现出路网大规模化和动态化特点，并且对最优化路径计算的时效性有较高的要求。对路径优化方法的研究应主动适应变化，在充分考虑约束条件的前提下结合搜索空间大小建立合适的搜索模型[2]。由于战场环境复杂多变，部队在庞大、复杂的路网体系中实施投送，需要运用高灵敏性、智能化方法来选出最优投送路径，传统的Dijkstra算法、Ford算法、SPFA算法、Floyd算法[3]在求解最短路径时，运算量较大、得出优化结果时间较长，不能并行计算且一般只适用于解决线性问题，而神经网络算法作为一种模拟人脑工作原理的算法，具有并行性、非线性运算等能力，可方便地用于大规模复杂问题求解。

1 建立神经网络算法模型

建立神经网络算法模型第1步是选择合适的神经网络类型，第2步是进行凸优化处理，第3步是利用MATLAB拓扑处理路网并进行神经网络数据训练。

1.1 选择神经网络类型

神经网络的结构可分为两类：一类是前馈式神经网络，一类是递归式神经网络[4]。前馈式神经网络神经元的输出不对自身改变做出影响；递归式神经网络神经元的输出会反馈到神经元的输入上，神经元可根据自身情况进行调节。分析二者的差别，在解决投送路径优化问题时，递归式神经网络更适合。本文选取递归式神经网络中的Hopfield神经网络建立算法模型[4，5]。

1.2 目标函数凸化处理

在寻找投送最优路径时，应先将问题转化为凸优化问题。构建路径选择函数作为目标函数，此时目标函数为凸函数，再进行优化求解。

Hopfield神经网络搜索路径时会出现陷入极小值点的情况，因此描述平衡点稳定性时要引入能量函数[6]，将能量函数作为目标函数，则目标函数E(V)表示为：

(1)

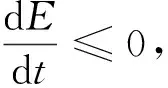
因此，经处理之后变成带约束的凸优化问题：

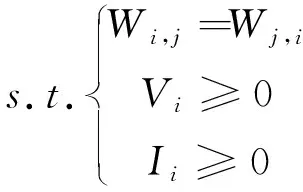
(2)

1.3 神经网络求解

路网有n个点时需要用n(n- 1)个神经单元，路网邻接矩阵中除对角元素外，每个元素都对应一个神经元。神经元只取值0或1两个状态，当Hopfield网络收敛到稳定的平衡状态时神经元状态函数δij:

神经元状态函数δij为1时弧在最优路径上，δij为0则不在最优路径上。

神经网络求解关键一步是要设置参数标准，这里可得最优路径的动力学方程为[7]：

(3)

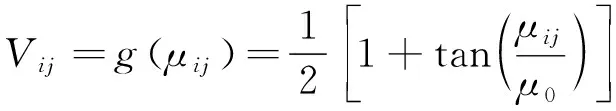
(4)

式中：mij是路网各节点之间的权重，a1,a2,a3,a4是惩罚系数。求解式(3)和式(4)组成的方程组，当神经网络收敛到稳定平衡状态时，此时输出神经元即是所要求的一条最优路径。

2 MATLAB软件处理

MATLAB软件有着强大的数值分析、工程绘图、设计仿真和可视化功能[8-9]，用软件进行路网拓扑化处理，然后调用神经网络工具箱，输入路段参数进行数据训练，最后对输出神经元质量进行分析。软件处理步骤：路网拓扑处理→Hopfield神经网络实现→调用神经网络工具箱→输入数据进行训练。

(1)路网拓扑化处理后不影响路段属性，并且可以将复杂公路网简化为节点互联的拓扑图，以便于问题求解。

(2)Hopfield神经网络要实现网络的稳定性，而能量函数是判定网络稳定性的基本方法，此处能量函数为E(V)。

(3)MATLAB神经网络工具箱中的神经网络分3类：第1类是有输入有输出且有反馈，第2类是无输入有输出，第3类是有输入有输出无反馈，显然这里应选第1类。

(4)路网拓扑图建立后，目标函数也随之确定，将路段实际值作为神经网络的训练数据来源。此时还需调整三种数据比例，即训练数据、验证数据以及测试数据比例；然后选取隐层神经元数量，一般取10；最后选择训练算法，从Levenberg-Marquardt、Bayesian Regularization、Scaled Conjugate Gradient中选择算法，一般选取L-M(Levenberg-Marquardt)算法[9-10]。

3 任务想定及仿真实现

3.1 作战想定及投送任务

基本作战想定：××部队奉命从贵阳出发，向徐州集结，遂行跨域特种打击任务。投送任务想定：投送人员共计5 000余人、各型装备1 000余件，采用公路投送方式。要求在×月×日×时×分前，完成全部投送任务，到达集结地域待命。

3.2 仿真实现

3.2.1 路网拓扑处理

根据投送任务想定，在实施部队投送时一般应选择高速公路或高等级公路进行，结合各战区范围内主要公路情况[11]，投送任务区域路网范围如图1所示。

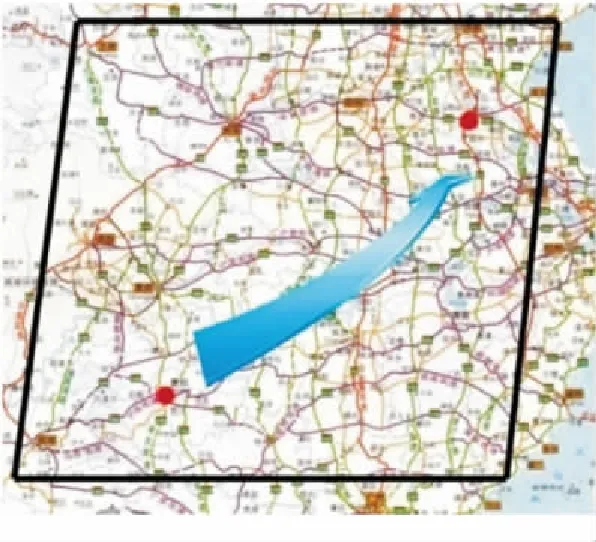
图1 投送任务区域路网

对此路网中有高速公路连接的重要城市进行编号，根据路网中节点相对位置和相关属性值，神经网络的输入节点为路网区域中的100个节点，将路网节点距离作为神经网络的输入数据，如表1所示。

表1 神经网络的输入数据

利用MATLAB进行拓扑处理，出发地贵阳标记为节点1，目的地徐州标记为节点100。拓扑图如图2所示。

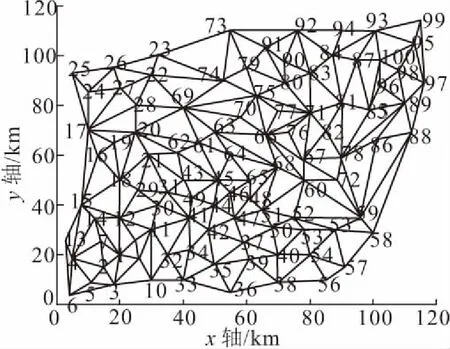
图2 投送任务路网拓扑

3.2.2 神经网络数据训练

在神经网络中，只有网络有良好的收敛性，才能避免陷入极小值点而出现局部最优解的情况[12]。在寻优过程中，同一个神经网络对数据的训练会出现不同的结果，这是局部的极值，随着训练次数增多，最终可以找到全局的极值，这个极值就是最优结果。MATLAB中神经网络训练结果如图3所示。

图3 神经网络训练结果

3.2.3 最优化路径的确定

从图3中看出，该神经网络经过58个迭代期后达到最优解。根据梯度与偏差值表现，输出神经元大致可分为4个阶段，即从局部最优到全局最优经历了4个阶段，分别如图4所示。

图4 路径选择结果

可知最优化的投送路径为：1-9-11-41-44-46-65-68-60-67-82-81-87-100，即沿着贵阳-遵义-同仁-吉首-常德-长沙-岳阳-鄂州-黄冈-阜阳-商丘-济宁-枣庄-徐州的方向进行投送。

3.2.4 输出神经元质量分析

神经网络训练输出数据的质量分析影响着最终优化结果，对输出神经元质量的分析要从三类数据最佳性能验证、验证梯度与学习次数关系分析、三类数据回归分析、数据误差分析等四个方面进行，分析结果如图5～图8所示。

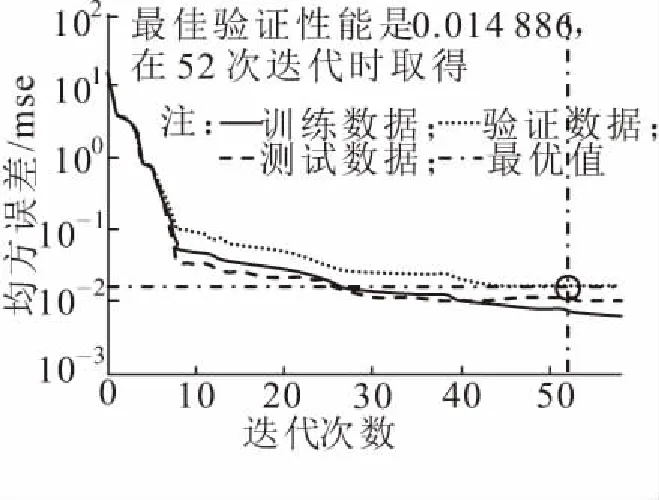
图5 训练、验证、测试数据的最佳性能验证

(1)分析三类数据的最佳性能验证曲线(图5)可知，可知最佳性能迭代次数为52次，迭代次数不少于52次时可以达到最佳性能，所以第58次迭代时最优结果可信度很高。从大的趋势上看，随着迭代次数的增加，模型在训练集上的误差会越来越小，但是次数显然不会无限增大，在某个值时会不再发生明显变化。

(2)分析验证数据的梯度与学习次数(图6)可知，可知迭代次数到58代时，验证数据可信度较高。由于波动，因此会使得学习次数增多，即收敛速度变慢，不过最终其会和全量梯度下降算法一样，具有相同的收敛性。由于目标函数为凸函数，则收敛于全局极值点。

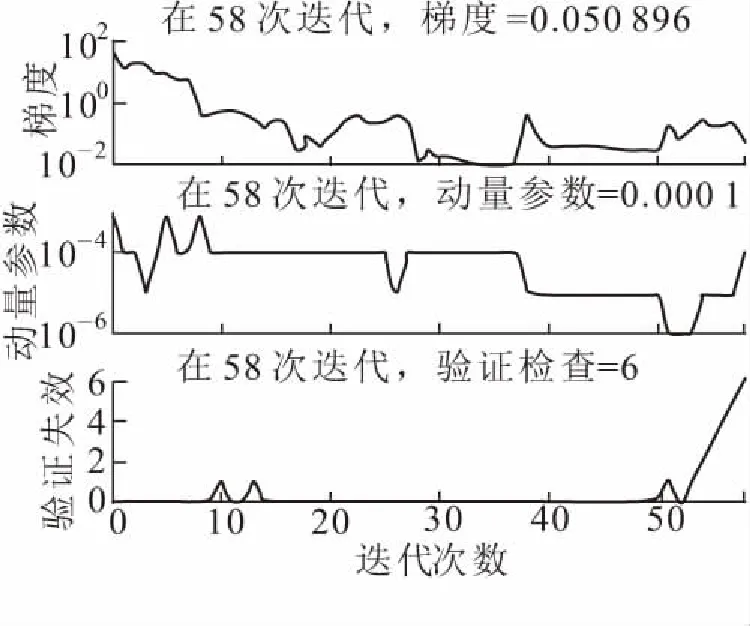
图6 验证数据的梯度与学习次数

(3)根据图7得到的结果可知，此时R值分别为0.999 50、0.998 83、 0.999 22，总体R值0.999 37，可知R值非常接近1，即MSE的值越小，其训练效果和模型拟合的更好。由此可见，此时训练得出的数据与模型吻合度较高，训练效果很好。

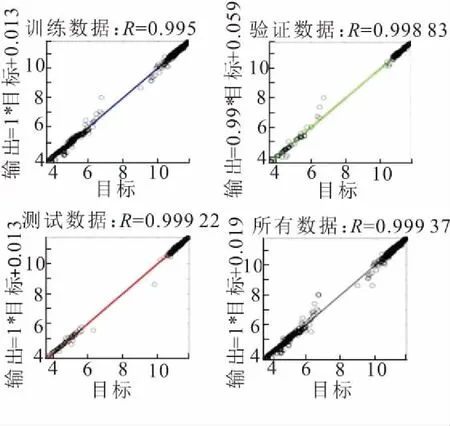
图7 训练数据、验证数据、测试数据回归分析

(4)分析图8误差直方结果可知，三类数据的误差集中在零点附近，即可认为可信度较高，得到的输出神经元质量较好。

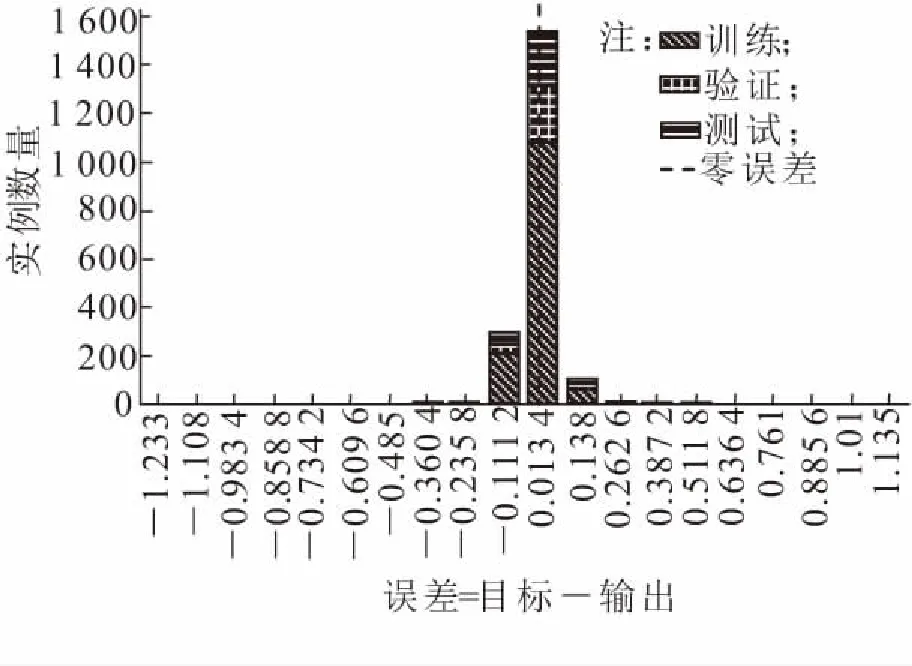
图8 训练数据、验证数据、测试数据误差直方

3.2.5 与传统算法优化结果的对比

利用传统算法如Dijkstra算法、Ford算法、SPFA算法、Floyd算法分别对路网进行最优路径求解，以不同算法的最优路径节点数为纵坐标、以运算时间为横坐标，得到结果对比如表2所示。可以发现，神经网络算法与Dijkstra算法、Ford算法、SPFA算法、Floyd算法相比，计算时间短，且最优路径节点数最少、优化效果最好，具有较强的计算优越性。

表2 不同算法结果对比

4 结论

由于未来部队投送会呈现距离更远、范围更大、路网更复杂的特点，本文采取的方法可推广至更加复杂的公路网络。在实际应用中还可充分利用神经网络算法大规模并行计算优势，组建适当规模的集群，解决更复杂、距离更远、环节更多的路径优化问题。