一种适用于FTM 的室内定位方法*

赵跃新 ，林 杰 ，2，刘 鹏 ，赵志佳

(1.陆军工程大学 指挥控制工程学院，江苏 南京 210007；2.解放军 32228 部队 24 分队，福建 福州 350000)

0 引言

位置服务作为物联网、移动互联网等新兴产业的关键服务，在智能交通、导航定位、人员监控以及紧急救援等方面有着广泛的应用[1-3]。 在室外开阔区域，以GPS、北斗为代表的全球导航卫星系统及其增强技术提供了准确的位置信息。但是在复杂的室内环境下，卫星导航信号容易受到遮挡而严重衰减，产生很大的定位误差，甚至失效[4]。 因此，室内定位技术得到了迅速研究与发展，涌现出基于WiFi、蓝牙、超宽带以及超声波等多种定位技术[5]，试图提供准确可靠的室内位置信息。

WiFi 技术具有普及率高、成本低的优势，在室内定位领域受到了重点关注[6-7]，其观测值主要包括传播时间(Time of Fight，ToF)、到达时间差(Time Difference of Arrival，TDoA)、到 达 角(Angle of Arrival，AoA)以及接收信号强度(Received Signal Strength，RSS)。 其中，ToF 是一种原理简单、适用范围广的观测值，但需要较高精度的时间同步。 IEEE 802.11-2016标准定义了精细时间测量(Fine Timing Measurement，FTM)协议[8]，在室内环境中可实现米级甚至分米级的测距精度，并且已经在商业WiFi 芯片中得到支持，比如 Intel 8260/8265 和高通 IPQ8065。

实现基于FTM 的精确室内定位仍面临诸多问题。其中，室内多径效应、信号干扰以及设备不稳定等因素可能引起异常测量值，导致定位误差明显增加[9]；同时，FTM 设备因为信号处理耗时，所以存在测量时间偏移，使得定位性能下降[10]。然而，已有异常值鲁棒滤波方法[11-12]的判别区间和抑制策略不能合理地区分处理异常值和正常值，并且现有FTM定位方法[13-14]需要提前校准时间偏移，不便于室内部署应用。

针对FTM 存在异常值以及时间偏移的问题，本文提出一种适用于 FTM 的室内定位方法。 该方法首先构建基于马氏距离的异常判别量，并且利用三段式权重函数计算加权矩阵，以此得到抑制异常值影响的M 估计鲁棒卡尔曼滤波，然后通过两步WLS实现待定位终端位置和时间偏移的联合估计，从而省去额外的校准过程。

1 FTM 基本原理

图 1 FTM 协议交互过程

FTM 协议采用典型的往返测时方式，其基本交互流程如图1 所示。 发起端首先向响应端发送FTM请求，然后响应端返回Ack 报文，接着双方进行FTM的测量报文交互。FTM 协议可通过多次往返测量来降低随机误差的影响，以第i 次往返交互为例进行说明，响应端在 t1(i)时刻发送 FTM 报文，发起端在t2(i)时刻接收到该报文，并在 t3(i)时刻发送 Ack 报文，然后响应端在t4(i)时刻接收报文，完成一次往返测量。 因此，可得N 次往返测量的平均传播时间为：

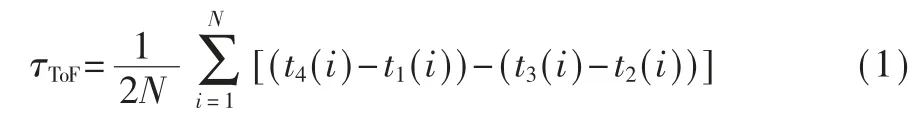
由于存在信号处理时延，因此报文的收发时刻无法记录真实值。 实际上，发送时刻 t1(i)和 t3(i)的记录值比真实值更小，而接收时刻 t2(i)和 t4(i)的记录值比真实值更大，从而使得往返时间测量值与真实值存在偏移Δτ，属于确定性时间偏移量。 此外，室内多径效应、信号干扰、设备故障等因素可能导致异常值，严重影响 FTM 定位精度。 因此，实现准确可靠的FTM 测时及其室内定位，需要重点克服异常值和时间偏移Δτ 的影响。

2 M 估计鲁棒卡尔曼滤波

针对FTM 测量值可能存在异常值，提出基于M 估计的鲁棒卡尔曼滤波，用于识别异常值并降低其影响。 FTM 以往返交互报文方式得到测距值其 中 c 为 信 号 传 播 速 度为 传 播 时 间 测量值。 以待定位的发起端与m 个响应端的真实距离作为系统状态 xk，实际观测向量 yk=[r1，k，r2，k，…，rm，k]T，其中 ri，k为发起端与第 i 个响应端在 k 时刻的测距值。 因此，状态方程和观测方程分别为：

其中，Fk和Hk分别为状态转移矩阵和观测系数矩阵，wk和 vk分别为过程噪声和观测噪声，并且相互独立，均服从零均值的高斯分布，其协方差矩阵分别为 Qk和 Rk。 由于待定位发起端处于静态，因此Fk和Hk均为单位矩阵，并且过程噪声很小，Qk可近似为零矩阵[15]。 通过统计处理测距值序列可得观测噪声协方差矩阵 Rk。 针对由式(2)和式(3)组成的状态空间模型，应用基于M 估计的鲁棒策略到线性卡尔曼滤波，可得具体步骤如下：

(1)时间更新：

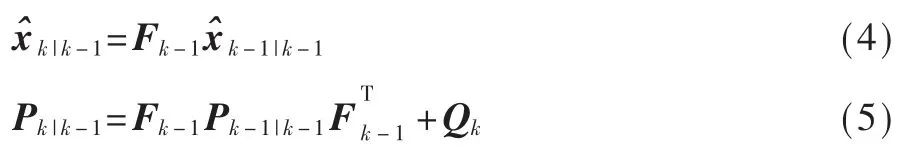
(2)观测更新：

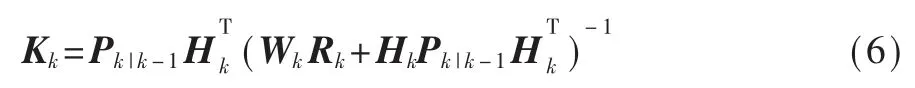
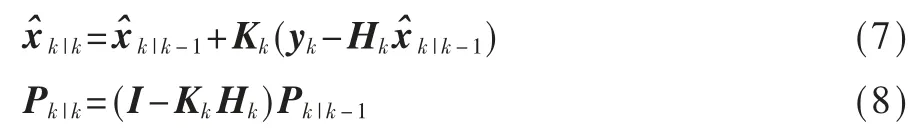
其中，加权矩阵 Wk用于调整 Rk的权重，影响异常值的处理效果。 为合理地确定加权矩阵的取值，构建了基于马氏距离的异常判别量：

对于自由度为1 的卡方分布，权重值的设置需要更精细。 对此，提出一种三段式权重函数t-Huber，其表达式为：

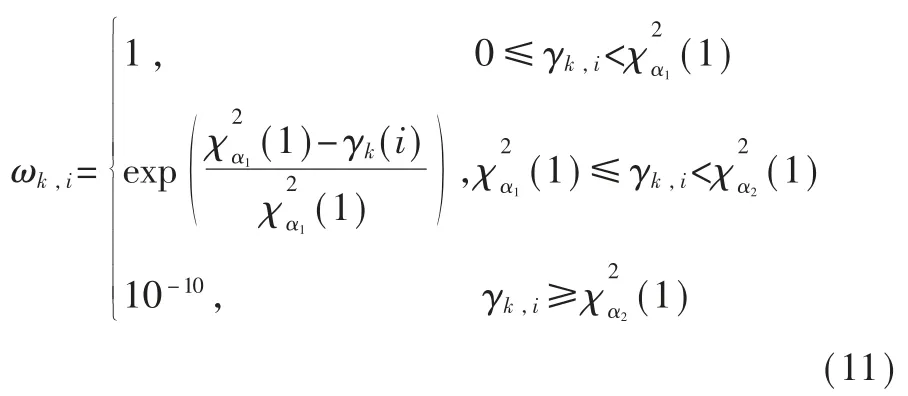
其中，ωk，i为权重矩阵的主对角线上第 i 个元素，α1=0.05 和 α2=0.005 为卡方分布的分位点，其确定异常判别的区间划分。 权重函数t-Huber 设置正常值的权重为1，对较小异常值进行指数降权，同时对很大异常值设定权重为10-10，这等同于剔除异常值，又能避免零权重引起滤波发散。

3 两步 WLS 定位

FTM 的时间偏移需要提前校准才能实现准确定位，不便于室内定位的部署应用。对此，提出一种联合估计待定位发起端位置和时间偏移的两步WLS 算法，从而可避免额外的校准过程。

已知响应端的坐标为 si=[xi，yi]T，i=1，2，…，m，待定位的发起端坐标为u=[x，y]T，距离偏移为Δd=cΔτ，从而可得测距值为：

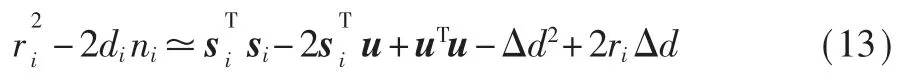
其中，di=||u-si||，同时忽略了二次噪声项。 令γ1=[uT，Δd，α]T以及 α=uTu-Δd2，从而式(13)的矩阵向量表达式为：

利用加权最小二乘求解式（14），可得：

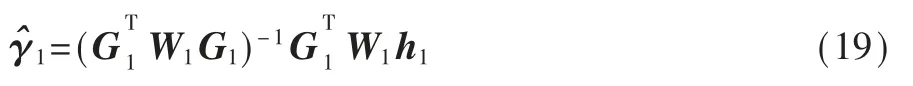
其中加权矩阵表达式为：

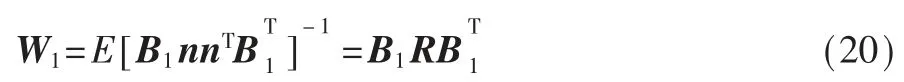
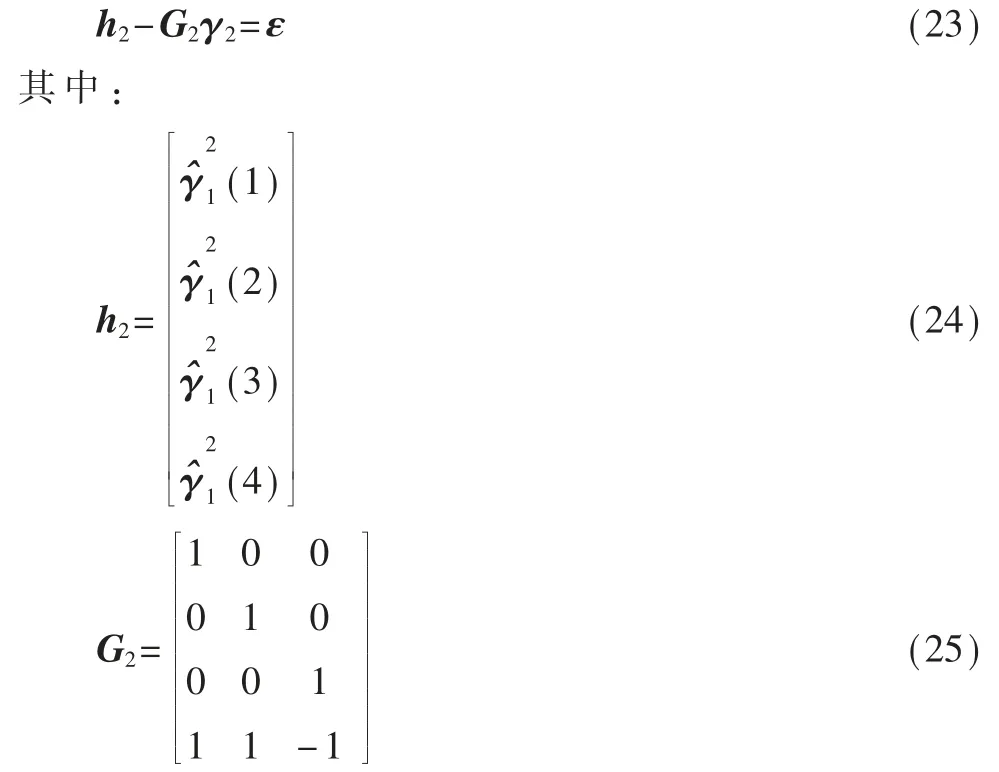
当估计误差 ei较小时，将式(22)代入式(23)可得：

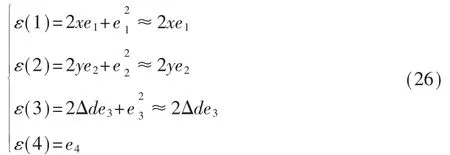
其中，ε(i)表示 ε 的第 i 个元素，并且舍去二次项误差。 然后，可以得到ε 的协方差矩阵为：

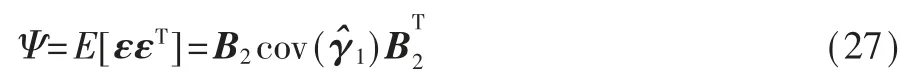
其中，B2=diag{2x，2y，2Δd，1}。 因此，可得第二步WLS的估计值为：

式中加权矩阵 W2=Ψ-1，其涉及的未知真实值 x、y、Δd 可用的前三个元素分别代替， 其性能 损失 可忽略。 最后利用排除模糊解，可得待定位发起端位置和距离偏移的估计值为：

其中，⊙表示 Schur 乘积，sgn(·)为符号函数。

图 2 两步 WLS 定位流程图

两步 WLS 定位的流程如图 2 所示。 第一步WLS通过m 个响应端的坐标和测距值来构造h1、G1以及计算加权矩阵 W1，然后估 计 得到和 协 方 差cov()，接着以此作为第二步WLS 的传递参数，用于构造h2、G2以及计算加权矩阵 W2，从而估计得到，最后排除模糊解可得发起端位置和距离偏移的估计值。

4 实验与分析

4.1 实验设备

FTM 实验设备包括发起端和响应端，如图3 所示。 其中， 发起端采用配装 Intel 8260 芯片的ThinkPad T450s 笔记本电脑， 安装低延迟内核的Ubuntu 16.04 系统， 并且修改无线网卡驱动以实现FTM 报文交互功能，其天线位于屏幕上方。 响应端使用商业无线路由器华硕RT-ACRH13，不需要任何配置修改即可支持FTM 测距功能。 由于响应端在FTM 测量过程中可能变更发射天线，因此将设备中心作为位置参考点，引入的误差不超过10 cm，相较于FTM 测距误差可以忽略。

图 3 FTM 实验设备

4.2 实验环境

实验环境为典型的室内大厅场景，如图4 所示，地面、墙壁、柱子和天花板引起多径效应，并且在实验过程中存在人员走动。FTM 实验设备在室内大厅的部署如图 5 所示， 其中 4 个 FTM 响应端的坐标分别为 s1=[0，0]Tm，s2=[0，10]Tm，s3=[16，0]Tm 以及 s4=[16，10]Tm，FTM 发起端作为待定位点均匀分布在中间区域的 20 个测试点。 FTM 实验设备的真实位置通过激光测距仪标定， 其误差为厘米级，所以可以忽略。 发送端和响应端选择WiFi 的157 信道，中心频率为 5.785 GHz， 带宽为 80 MHz， 在每个待定位点上进行 100 次 FTM 测量， 每次 FTM 测距间隔0.5 s。

图4 室内大厅实验场景

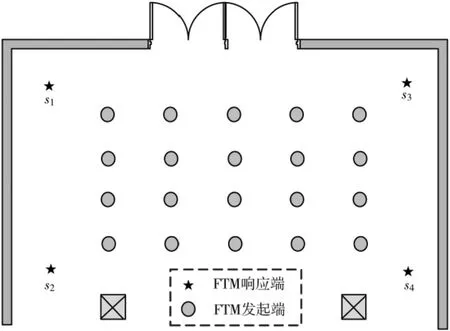
图5 FTM 实验设备部署图

4.3 实验结果

每个响应端的FTM 测距值及其异常值滤波情况基本类似，因此以响应端为例，选取其中存在较多异常值的测距结果进行分析，如图6 所示。 通过M 估计鲁棒卡尔曼滤波抑制异常值，相较于Huber权重策略[8]，本文提出的 t-Huber 权重函数不仅能更好地降低随机观测噪声的影响，还可以明显抑制异常值，尤其当异常值较大时，其抑制效果更为显著。 FTM 的测距平均值约为 4.04 m，而真实测距值为 2.75 m，所以距离偏移约为1.29 m(时间偏移约为 4.3 ns)。 考虑 100 次 FTM 测距值，可以得到 4 个FTM 响应端的平均时间偏移和距离偏移，如表1 所示，其差异较小，与FTM 测距误差相比可以忽略。

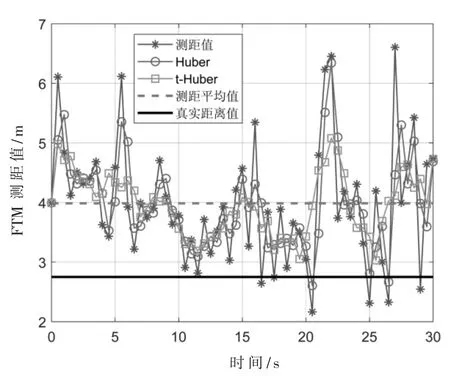
图6 FTM 测距值及其异常值滤波

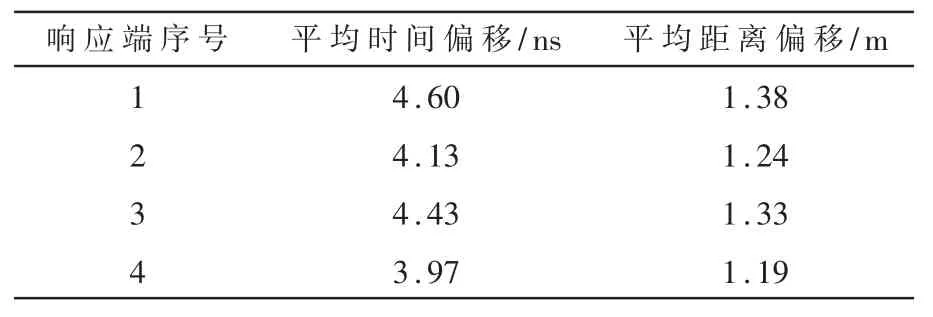
表1 FTM 测量的平均时间偏移和距离偏移

FTM 定位误差的累积分布如图 7 所示。 对比分析的三种定位方法均是采用两步WLS 算法， 区别在于异常值和时间偏移的处理。 其中，未校准方法直接通过原始的测距值进行定位，所以同时受到异常值和时间偏移的影响，定位误差最大；联合估计方法和已校准方法均采用本文提出的鲁棒卡尔曼滤波来抑制异常值，所以没有产生很大的定位误差，并且 80%误差分别小于 1.5 m 和 1.2 m， 两者的定位精度较为接近，但是联合估计方法不需要时间偏移的校准过程。

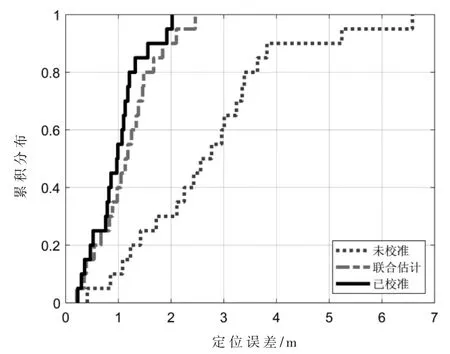
图7 FTM 定位误差的累积分布

5 结束语

本文针对FTM 存在异常值和时间偏移的问题，提出了一种适用于FTM 的室内方法。 该方法通过基于马氏距离的判别量以及三段式权重函数t-Huber，得到M 估计鲁棒卡尔曼滤波，然后利用两步WLS定位算法实现发起端位置和时间偏移的联合估计。室内大厅的FTM 定位实验结果表明所提方法可以降低小异常值影响，又能剔除大异常值，而且联合估计定位和已校准定位的80%误差分别不超过1.5 m 和 1.2 m，两者定位精度较为接近，但是前者不需要校准过程。 因此，本文所提出的定位方法可以很好地适用于FTM，也能应用于5G、超宽带等ToF 定位场景。