基于灰狼算法的电力系统无功优化控制

任振宇，张 师

(1.内蒙古电力集团有限责任公司，呼和浩特 010000；2.东北电力大学 电气工程学院，吉林 吉林 132012)

0 引 言

随着能源互联网的发展，越来越多的新型发电形式并网，电网运行工况日益复杂，为电力系统无功优化控制带来了挑战[1]。随着电力系统运行工况的频繁变化，无功优化控制也应该相应调整以使系统运行于最优状态[2-4]。对于现代高电压等级、大功率传输、交直流混联的电力系统而言，对无功优化算法提出了更高的要求[5-8]。

关于电力系统无功优化控制方面已经取得了一些成果。文献[9]提出了一种将模糊逻辑、模拟退火算法与免疫算法相结合的改进免疫遗传算法，为避免陷入局部最优，根据模糊逻辑得到可变交叉变异算子，利用退火免疫算法选择抗体，用免疫算子更新个体，增强群体多样性，避免局部最优。文献[10]基于三点估计法原理提出一种综合考虑风电场出力和负荷的随机波动的系统静态电压稳定程度的分析方法。文献[11]采用改进退火蚁群算法对配电网进行了无功优化，减小了系统总网损。文献[12]基于改进遗传算法进行电力系统无功规划，对算法中优化等复杂非线性优化问题中容易发生“早熟”和收敛速度慢等问题予以改进，提高了全局收敛性。

尽管风电并网系统的无功优化控制已经取得了许多研究进展，但是如何提高收敛速度和优化效果仍然是现代电力系统亟需的。文献[13]采用灰狼算法优化水轮机PID控制,使水电可以稳定地跟踪系统工况的变化。目前尚未有研究将灰狼算法应用到电力系统无功优化中，因此灰狼算法能否在电力系统无功优化中取得更好的效果有待考证。基于此，该文将基于灰狼算法实现电力系统无功优化控制，并通过10机39节点系统对文中方法予以验证。

1 灰狼算法

灰狼优化算法(Grey Wolf Optimizer，GWO)是由澳大利亚格里菲斯大学学者 Mirjalili 等人于2014年提出来的一种群智能优化算法。该算法是源于灰狼捕食猎物活动的启发而开发的一种优化搜索方法，它具有较强的收敛性能、参数少、易实现等特点，其主要步骤如图1所示。

图1 灰狼算法优化流程Fig.1 Flow chart of optimization with grey wolf algorithm

当设计 GWO 时，首先需构建灰狼社会等级层次模型。选取狼群中适应度最好的3匹灰狼依次标记为α、β和δ，其他的灰狼标记为ω，GWO的优化过程主要由每代种群中最好的3个解α、β和δ完成。灰狼捜索猎物时会逐渐地接近猎物并包围它。

潜在猎物(最优解)可以被灰狼有效识别，搜索过程主要靠α、β和δ灰狼的指引来完成。由于一些优化过程中解空间具有未知性，以致GWO无法确定猎物的精确位置。所以在模拟灰狼(候选解)的搜索行为时，令α、β和δ具有较强识别潜在猎物位置的能力。可以在每次迭代过程中，保留当前种群中最好的3只灰狼(α、β和δ)，然后根据它们的位置信息来更新其他灰狼的位置。具体搜索过程可以用以下模型来描述：

式中：Xα、Xβ和Xδ分别为α、β和δ的位置向量；Dα、Dβ和Dδ表示候选狼与最优3匹狼之间的距离；A1、A2和A3为搜索猎物时的系数，当|A|>1时灰狼之间应尽量分散在各个区域搜索猎物，当|A|<1时灰狼应集中搜索某个区域的猎物；C1、C2和C3为随机权重。

攻击猎物过程中，通过调节A，使A在[-1,1]区间，即搜索下一时刻位置在当前灰狼与猎物之间的任意位置上。

寻找猎物时，候选灰狼主要依赖α、β和δ的信息，当|A|>1时属于分散模型，GWO采用全局搜索，C相量的范围为[0,2]，为猎物提供了随机权重，C的合理取值有助于避免算法陷入局部最优。

2 基于狼群算法的电力系统的优化运行

无功优化目标为系统总网损最小，可以表示为

式中：i，j为节点号；n为总节点数；Gij为i节点、j节点间支路电导；Ui、Uj为i节点、j节点的电压幅值；δi、δj为i节点、j节点的电压相角。

等式约束为潮流方程：

式中：ei和fi分别为i节点电压的实部和虚部；Bij为i节点和j节点互导的虚部。对于PV节点，还需补充1组方程：

优化结果的可行域还要考虑不等式约束，即电压约束和无功约束：

Umin≤U≤Umax

(1)

QG.min≤QG≤QG.max

(2)

式中：QG为发电机的无功功率。

式(1)是由于电力系统对电能质量的约束决定的，各节点电压需要满足幅值约束；式(2)是由发电机的运行极限决定的，无功功率不能越限。

3 算例分析

采用10机39节点系统算例，如图2所示。设置基准功率100 MVA，算法中的种群数为20，更新代数为300，改变机端电压调压范围为[0.95, 1.1]，变压器分接头的非标准变比为[0.9, 1.1]，分度值0.0025，无功补偿为[0,0.5]，分度值0.1。

图2 新英格兰10机39节点标准测试系统Fig.2 New England 10-machine 39-node standard test system

设可调节机端电压的节点为bus30、bus31、bus32、bus33、bus34、bus35、bus36、bus37、bus38、bus39；12个变压器均为有载调压变压器，可以改变分接头；无功补偿节点为bus7和bus8。

优化前系统总网损为0.437 12 p.u.，优化后系统总网损为0.403 68 p.u.，算法有效。

为体现GWO算法的优越性，还将其他算法用于该系统的无功优化，其他算法包括鲸鱼群算法(Whale Optimization Algorithm，WOA)、改进遗传-粒子群优化(Genetic Algorithm-Particle Swarm Optimization，GAPSO)和飞蛾扑火算法(Moth-Flame Optimization，MFO)。

各种算法控制变量和优化后的系统网损如表1所示，控制变量如图3所示。

表1 优化前后的结果Table 1 Results before and after optimization

从图3可以看出：GAPSO的变压器变比改变较多，7、8节点无功补偿量较大，效果较好；但是相比之下GWO的无功补偿量更少，但优化效果优于GAPSO。GWO算法的控制变量中，30、31、32、33、36、37、38、39节点的机端电压均高于GAPSO的机端电压。因此，并非无功补偿越多越好，适当的无功补偿量会使系统更经济。

图3 不同算法优化前后控制变量Fig.3 Control variables before and after optimization by different algorithms

从表1可以看出，GWO寻优效果最好，优化后总网损最少，为0.403 68 p.u.。

不同优化算法的优化过程中的收敛曲线如图4所示。从图4可以看出，WOA和GAPSO收敛速度较快，尽管GWO前150次更新收敛效果不及其他算法，但GWO不断寻找全局最优解，最终寻找到了比其他算法更优的最优解。

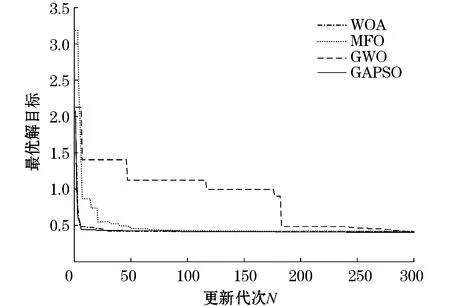
图4 收敛曲线Fig.4 Convergence curve

从以上分析可知：相比于其他优化算法，采用GWO寻优效果最好；尽管GWO的随机初始目标值不够优越，但随着更新代次的增加，GWO快速向全局最优收敛。

4 结 语

1)通过与鲸鱼群算法、改进遗传-粒子群优化算法、飞蛾扑火算法对比，表明灰狼算法能够更好地寻找最优值，优化电力系统无功分布，提高系统运行的经济性。

2)从GWO的控制变量可以看出，并非无功补偿容量越多越好，适当的无功补偿可以使系统运行在最优经济水平。

3)GWO在前150次更新时效果不够理想，180次后迅速找到最优解，因此保证足够多的更新次数会使GWO效果更加显著。