奖惩机制下规范建筑垃圾清运行为的演化博弈＊

■ 郭晓剑 胡欢

江西理工大学经济管理学院 赣州 341000

0 引言

建筑垃圾占世界生产所有垃圾的很大比重，大量的产生量和具体的资源使这条废物流成为当前全球政策的一个重要焦点，例如欧盟委员会已在循环经济一揽子计划中提出了这一废物流的新目标和策略[1]。我国在“十三五”中就提出了对于创新环境治理理念和方式，要实行最严格的环境保护制度，加快城镇垃圾处理设施建设，完善收运系统，形成政府、企业、公众共治的环境治理体系，实现环境质量总体改善，这是我国推进现代化社会、建设美丽中国的必然道路。在建筑垃圾清运方面，虽然国家颁布了《建筑垃圾管理规定》等规则，各地也出台了相应的惩罚管控措施，然而，建筑垃圾清运过程当中的运输超载，车容车貌不整、未封闭、跑冒滴漏，偷倒乱倒，闯禁等不良行为屡禁不止，对社会生活和社会安全造成了极大的危害。相对的是，环保部门督促整改下需要的成本必定不低，各建筑垃圾清运承包商也需要牺牲一些自身利益来进行相应的整改。在此背景之下，若能使得建筑垃圾清运承包商意识到这些不良行为的收益远小于整改之后的收益并对现有状况自觉整改，与此同时，相关的环保部门就能减少监管机制下的投入成本，形成一个良性循环。但是，就目前形势来看，要想达成这一良性循环还有一定难度，各建筑垃圾清运承包商对于眼前利益的追求远大于社会环境的要求，政府的环境部门的监管实施和成本难度也较大。

目前，国内外关于垃圾清运的研究层出不穷，Silva等研究了近年来建筑垃圾再生在新建筑材料中的应用和开发的新进展[2]。Wai 等发现建筑垃圾的可回收性和运输垃圾所需的能源受区域变量的影响[3]。叶晓甦等以区分建筑垃圾资源化利益相关者为基础,运用成本效益分析法核算建筑垃圾处置方式不同而产生的成本与效益,并给出三种相关对策[4]。贺娟等运用物质流分析法和全过程管理理论定量分析了中国建筑垃圾资源化利用率低的现状，并基于此提出了中国建筑垃圾资源化率的提升建议路径[5]。但是，这些研究仅仅停留在建筑垃圾的回收处理和再利用上，对于建筑垃圾清运的行为过程却鲜有人研究。演化博弈把群体的行为调整看做一个整体的系统[6]，以使得个人行为到群体行为的形成机理以及涉及到的各种因素都归入到演化博弈模型中，具有实际意义，该理论在生物学、经济学、金融学和管理学等学科领域均有很大用场。王洪利等从演化博弈视角分析共享经济将有助于深入理解其中参与主体行为演化过程和趋势[7]。Hasan 等从电网的防御者和网络攻击者博弈出发建立了一种新的可以减少损失的电力防御模型[8]。傅沂等采用演化博弈分析出养老地产发展模式不完全契约性的成因是开发运营周期长、有限理性的参与主体和复杂的开发运营契约[9]。刘旭旺等对评标过程中技术专家与商务专家之间的对立与合作关系进行博弈演化，并提出要适时改变对策以提高评标的公平性[10]。当然，有很多选择博弈一方为政府的研究，例如朱立龙[11]，Sun[12]，陈真玲[13]等以分析政府与相关社会问题的关系。本文以演化非对称博弈为基础，对环保部门和建筑垃圾清运承包单位的投入成本和风险的收益研究，分析现实中双方的行为策略选择。

1 模型的假设和构建

1.1 模型假设

在本文所构建的演化博弈模型当中的两个参与群体分别为政府环保部门和建筑垃圾清运承包单位，对博弈双方提出以下假设：

假设1：对于该模型中的参与人1（政府环保部门）和参与人2（建筑垃圾清运承包单位），假设参与双方都是有限理性的。

假设2：政府环保部门的策略选择方式有两种，选择进行严格监管，概率为x（0＜x＜1）;选择宽松监管，概率为（1-x）。同样，建筑垃圾清运承包单位也有两种策略选择方式，选择对现有情况整改，概率为y（0＜y＜1）;选择维持现状，即不整改，概率为（1-y）。

假设3：环保部门进行严格监管时的成本为Cs，宽松监管时的成本为Cp，明显可知Cs＞Cp＞0；建筑垃圾清运承包单位进行整改的成本为Cr，不整改的成本为Cq,明显可知Cr＞Cq＞0,且每一建筑垃圾清运承包的承包价格为G(包含成本)，即整改和不整改两种情况下的最终收益分别为G-Cr和G-Cq。

假设4：当建筑垃圾清运承包单位不进行整改时，周围生活居民在受到建筑垃圾清运承包单位运输建筑垃圾时的交通安全风险、生活环境质量变差等影响时会有θ（0＜θ＜1）的概率向环保部门举报，或当环保部门进行严格监管时发现违规情况，环保部门将对相关企业进行罚款，为f。同时，若建筑垃圾清运承包单位进行整改，该单位将会受到环保部门赞扬并提高单位知名度并获得更多的承包项目，收益为Pc，且环保部门也会因为环境质量变好而受到上级的鼓励和嘉奖，收益为Ph。

1.2 模型构建

基于以上假设，构建出环保部门与建筑垃圾清运承包单位之间的演化博弈收益矩阵，如表1所示。

表1 演化博弈的收益矩阵

通过表1的演化博弈收益矩阵，设环保部门选择严格监管时的期望收益、选择宽松监管时的期望收益和政府的平均收益分别为M1,M2和Mˉ:

同理，设建筑垃圾清运承包单位进行整改使得期望收益、不整改时的期望收益和平均收益分别为N1,N2和:

根据Malthusian 动态方程[14-18],由（1），（2），（3）可得环保部门严格监管比例下的复制动态方程为：

令R(x) = 0,可得x1= 0,x2= 1,y3=

同理，由（4），（5），（6）可得建筑垃圾清运承包单位整改比例下的复制动态方程为：

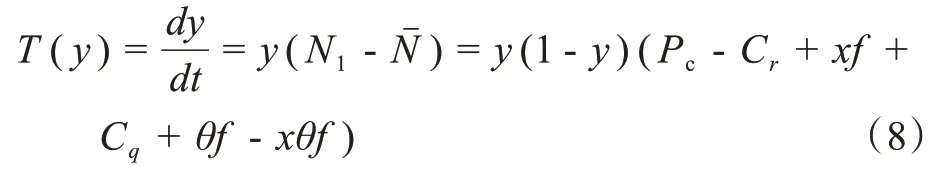
表2 系统局部均衡点具体取值

令T(y) = 0,可得y1=0,y2=1,x3=

由此可得上述博弈的系统均衡点为：（0，0），（1，0），

2 演化博弈模型分析

根据由复制动态方程（7），（8）可得：

根据Friedman[19-20]的研究，系统的雅克比矩阵为：

当满足以下两个条件，这时演化稳定策略（ESS）为复制动态方程的均衡点。

（1）trJ=a11+a22＜0(迹条件) （2） detJ==a11a22-a12a21＞0(雅各比行列式条件)

系统局部均衡点的取值如表2所示：

由于在（x3，y3）处a11+a22=0 不满足trJ=a11+a22＜0 这一迹条件，所以（x3，y3）肯定不是演化的稳定均衡点，所以γ1，γ2的值就不再计算。

推论1：当Cs-Cp-Ph＞(1-θ)f且Cr-Cq＞f+Pc时，系统相位演化图如图1。此时的系统演化稳定策略为（0，0），策略组合为（宽松管理，不整改）。

图1 推论1下的演化相位图

证明1：根据系统动态方程及其判断条件求出各均衡点的迹和雅各比行列式的值，并判断相应稳定性。当Cs-Cp-Ph＞(1-θ)f且Cr-Cq＞f+Pc时，系统均衡点的稳定性分析如表3。

表3 系统均衡点的稳定性分析

根据表3可以判定推论1推论正确。由推论1可知，当严格监管的投入收益比宽松监管的投入收益小且建筑垃圾清运单位的整改投入收益比不整改投入收益小时，建筑垃圾清运单位处于自身利益最大化会选择不整改，而此时政府环保部门得到的罚款和上级嘉奖并不足以支持环保部门进行严格监管，于是环保部门选择宽松监管。

推论2：当Cs-Cp-Ph＜(1-θ)f且Cr-Cq＞f+Pc时，系统相位演化图如图2。此时的系统演化稳定策略为（1，0），策略组合为（严格管理，不整改）。

图2 推论2下的演化相位图

证明2：根据系统动态方程及其判断条件求出各均衡点的迹和雅各比行列式的值，并判断相应稳定性。当Cs-Cp-Ph＜(1-θ)f 且Cr-Cq＞f+Pc时，系统均衡点的稳定性分析如表4。

表4 系统均衡点的稳定性分析

根据表4可以判定推论2推论正确。由推论2可知，建筑垃圾清运单位的整改投入收益比不整改投入收益小，但是政府环保部门的严格监管的投入收益比宽松监管的投入收益大，此时虽然建筑垃圾清运单位处于自身利益最大化会选择不整改，但是环保部门得到的罚款和上级嘉奖比严格监管投入的成本大，因此选择进行严格监管。

推论3：当Cs-Cp-Ph＜0 且Cr-Cq＜θf+Pc时，系统相位演化图如图3。此时的系统演化稳定策略为（1，1），策略组合为（严格管理，整改）。

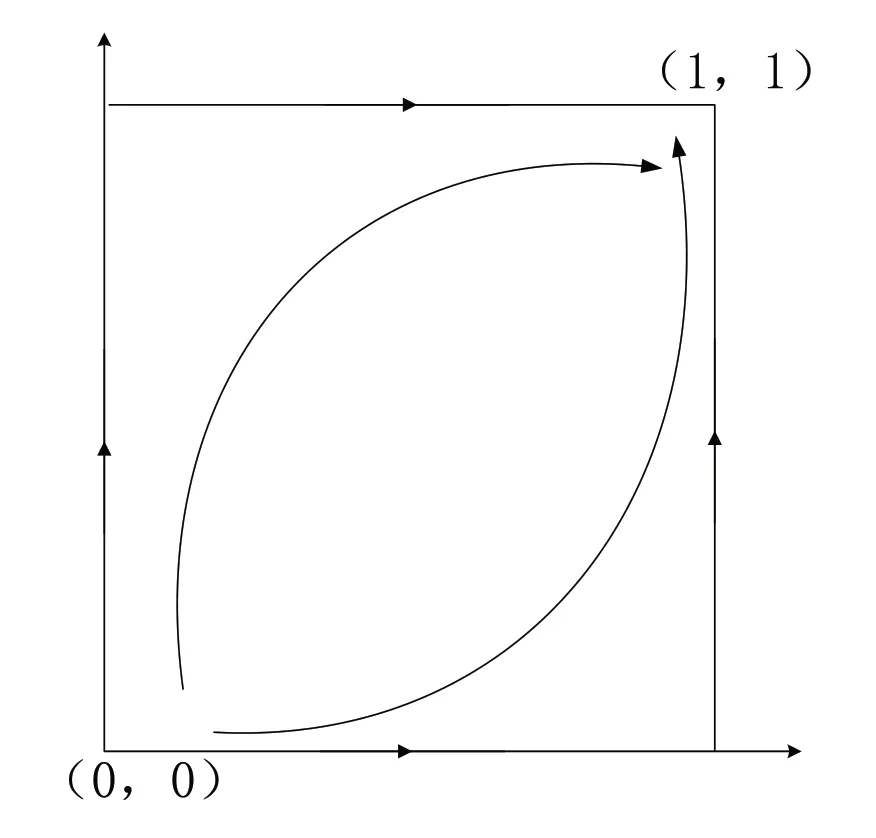
图3 推论3下的演化相位图

证明3：根据系统动态方程及其判断条件求出各均衡点的迹和雅各比行列式的值，并判断相应稳定性。当Cs-Cp-Ph＜0 且Cr-Cq＜θf+Pc时，系统均衡点的稳定性分析如表5。

根据表5可以判定推论3推论正确。由推论3可知，建筑垃圾清运单位的整改投入收益比不整改投入收益大且政府环保部门的严格监管的投入收益比宽松监管的投入收益大，此时环保部门得到的罚款和上级嘉奖比严格监管投入的成本大且建筑垃圾清运单位的罚款数目已经超过了整改后的收益总和，因此双方会分别选择进行严格监管和整改。

表5 系统均衡点的稳定性分析

推论4：当Cs-Cp-Ph＞0 且Cr-Cq＜θf+Pc时，系统相位演化图如图4。此时的系统演化稳定策略为（0，1），策略组合为（宽松管理，整改）。

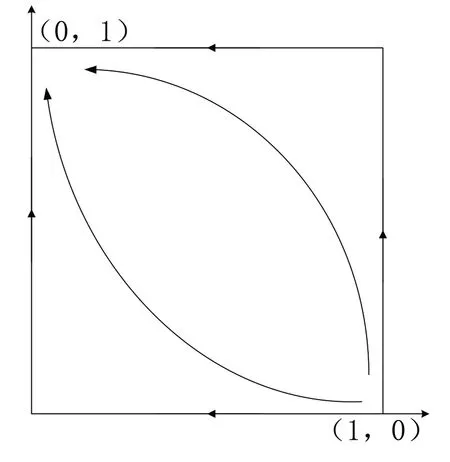
图4 推论4下的演化相位图

证明4：根据系统动态方程及其判断条件求出各均衡点的迹和雅各比行列式的值，并判断相应稳定性。当Cs-Cp-Ph＞0 且Cr-Cq＜θf+Pc时，系统均衡点的稳定性分析如表6。

根据表6可以判定推论4推论正确。由推论4可知，建筑垃圾清运单位的整改投入收益比不整改投入收益大，而政府环保部门的严格监管的投入收益比宽松监管的投入收益小，此时建筑垃圾清运单位的罚款数目仍超过了整改后的收益总和，继续选择进行整改。但是环保部门得到的罚款和上级嘉奖之和小于了严格监管投入的成本，所以选择进行宽松监管。

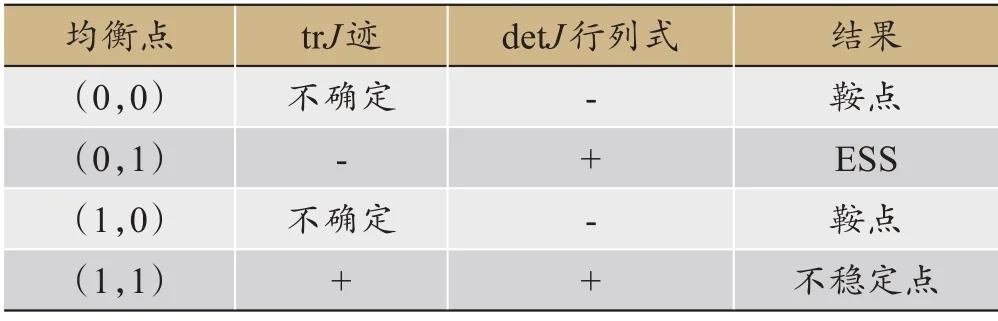
表6 系统均衡点的稳定性分析

推论5：当0＜Cs-Cp-Ph＜(1-θ)f且θf+Pc＜Cr-Cq＜f+Pc时，系统相位演化图如图5，此时的系统不存在稳定均衡点，属于博弈过程中的过渡期。

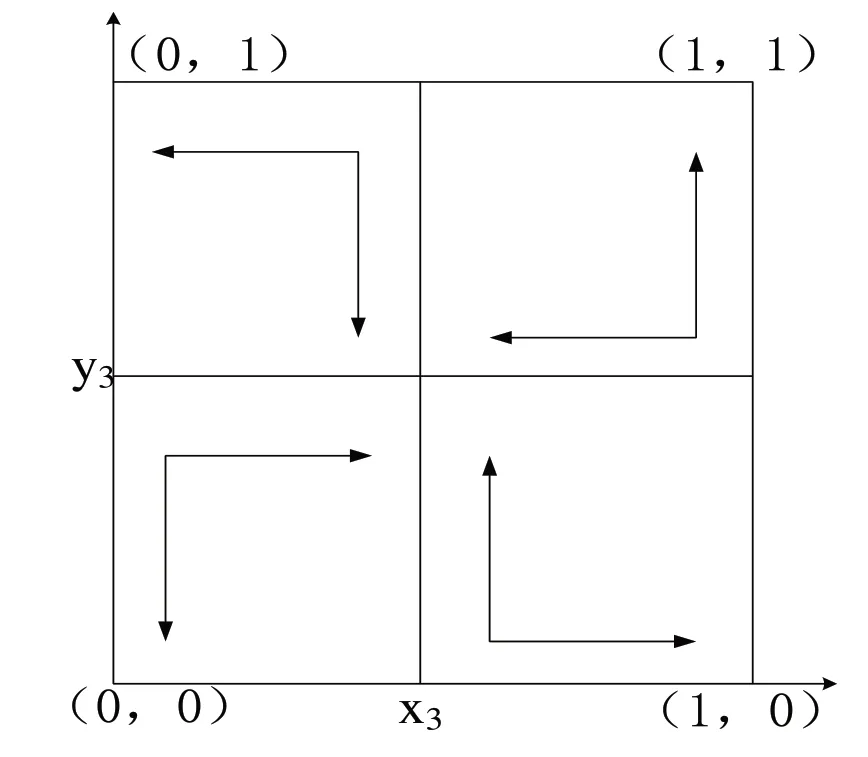
图5 推论5下的演化相位图

证明5：根据系统动态方程及其判断条件求出各均衡点的迹和雅各比行列式的值，并判断相应稳定性。当0＜Cs-Cp-Ph＜(1-θ)f且θf+Pc＜Cr-Cq＜f+Pc时，系统均衡点的稳定性分析如表7，可以判定推论5推论正确。

表7 系统均衡点的稳定性分析

由推论5可知，此时没有博弈稳定均衡点，博弈双方根据各自的利益最大化的要求向最接近自己的博弈稳定点靠拢，这时是一种过渡时期，此时的系统演化方向不确定，双方需要进行各自策略和相对应的条件（例如罚款数额）的调节，在这种情况下政府更应该谨慎策略，若是选择策略失误就会导致双方整体收益变差。

根据推论1、2、3、4、5 可知，双方博弈过程是一个循环过程，对于社会整体利益来说，最完美的情况为推论4，即政府在宽松监管的同时建筑垃圾清运单位主动进行整改，这就需要我们进行调节奖惩措施，争取较快的进入和保持博弈情况维持在推论4 下，具体仿真分析见下文。

3 仿真分析

为了更为直观的对不同情况下政府环保部门与建筑垃圾清运单位之间的演化博弈策略进行研究，利用MATLAB 软件对4 种不同情况的进行仿真来模拟参数变化时相应演化博弈的策略改变的结果。

设固定值Cs=20,Cp=12,Cr=30,Cq=20,θ=0.5,x,y的初值属于{0.2,0.4,0.6,0.8}中任意两值组合。

（1）设Ph=1,Pc=1,f=4，满足推论1 条件Cs-Cp-Ph＞(1-θ)f且Cr-Cq＞f+Pc，仿真结果如图6所示。

图6 稳定点（0，0）的仿真结果

由上图可知模拟结果与推论1 一致，此时的上级嘉奖、建筑垃圾清运单位知名度和违规罚款都处于较低的状态，可以把推论1看做是双方博弈的初始状态，在推论1 的条件下，双方逐渐靠近稳定点（0，0）并选择进行（宽松监管，不整改）。

（2）设Ph=9,Pc=1,f=8，满足推论2 条件Cs-Cp-Ph＜(1-θ)f且Cr-Cq＞f+Pc，仿真结果如图7所示。

图7 稳定点（1，0）的仿真结果

由上图可知仿真结果与推论2一致，同时可以看出，推论1由于某种条件会转变为推论2，即上级政府加大对垃圾清运的要求，向下级环保部门施压并提高了对建筑垃圾清运工作管理的嘉奖，即提高了Ph的值，下级环保部门应上级要求加大对清运建筑垃圾违规行为的处罚f，此时双方逐渐靠近稳定点（1，0），即选择进行（严格监管，不整改）。

（3）设Ph=9,Pc=5,f=12，满足推论3条件Cs-Cp-Ph＜0且Cr-Cq＜θf+Pc，仿真结果如图8所示。

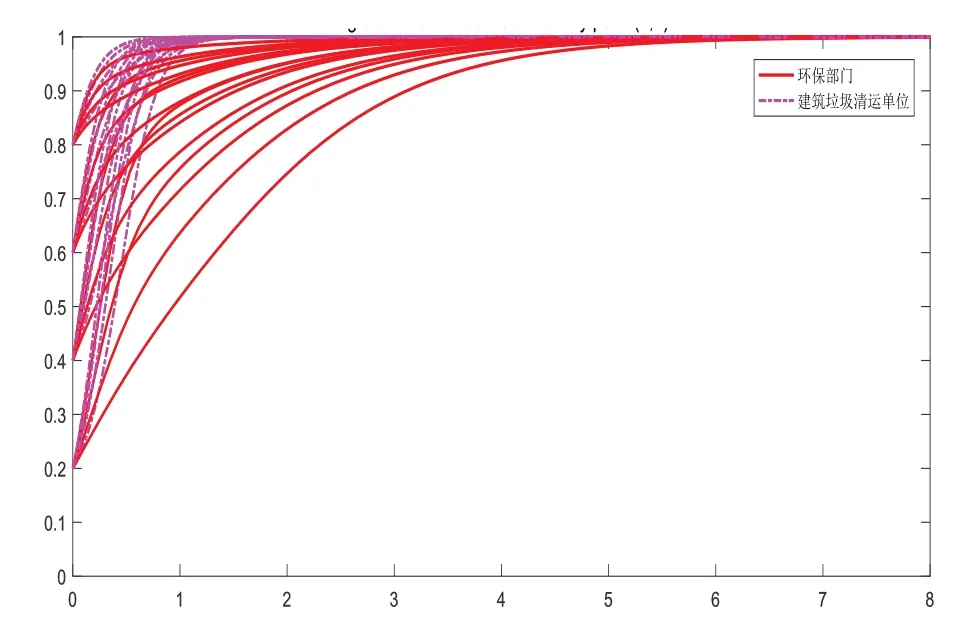
图8 稳定点（1，1）的仿真结果

由上图可知仿真结果与推论3一致，此时，政府环保部门由于上级压力进行严格监管，同时采取了更加严格的奖惩措施，例如增加罚款的金额f和加大对主动进行整改的单位进行推广，加强这些单位的知名度和认可度Pc。此时大部分的建筑垃圾清运单位为保证自身收益选择进行整改以免于罚款，双方逐渐靠近稳定点（1，1），即选择进行（严格监管，整改）。

（4）设Ph=1,Pc=6,f=10，满足推论4条件Cs-Cp-Ph＞0且Cr-Cq＜θf+Pc，仿真结果如图9所示。

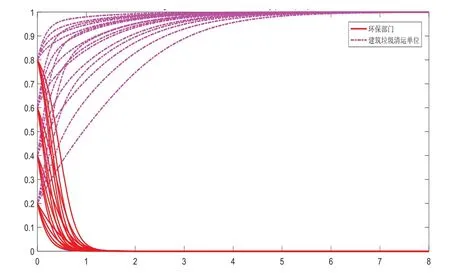
图9 稳定点（1，1）的仿真结果

由上图可知仿真结果与推论4一致，此时，建筑垃圾清运单位基本选择进行整改，而上级政府过了推广整改的时期减少了对下级政府环保部门的嘉奖Ph，此时若要保证建筑垃圾清运单位继续进行自觉整改，需要维持奖惩力度，基本保持推论3中违规罚款的金额f与对主动进行整改的单位的推广和加强这些单位的知名度、认可度Pc。政府环保部门不需要进行对监管的投入而选择进行宽松监管的同时，建筑垃圾清运单位仍然选择继续进行整改，这种情况是最理想的状态，双方逐渐靠近稳定点（1，1）并选择进行（宽松监管，整改）。

（5）由于推论5属于演化的过程时期，此时的演化稳定点不确定，任取0＜Cs-Cp-Ph＜(1-θ)f且θf+Pc＜Cr-Cq＜f+Pc中的点进行仿真，所得结果如图10所示。

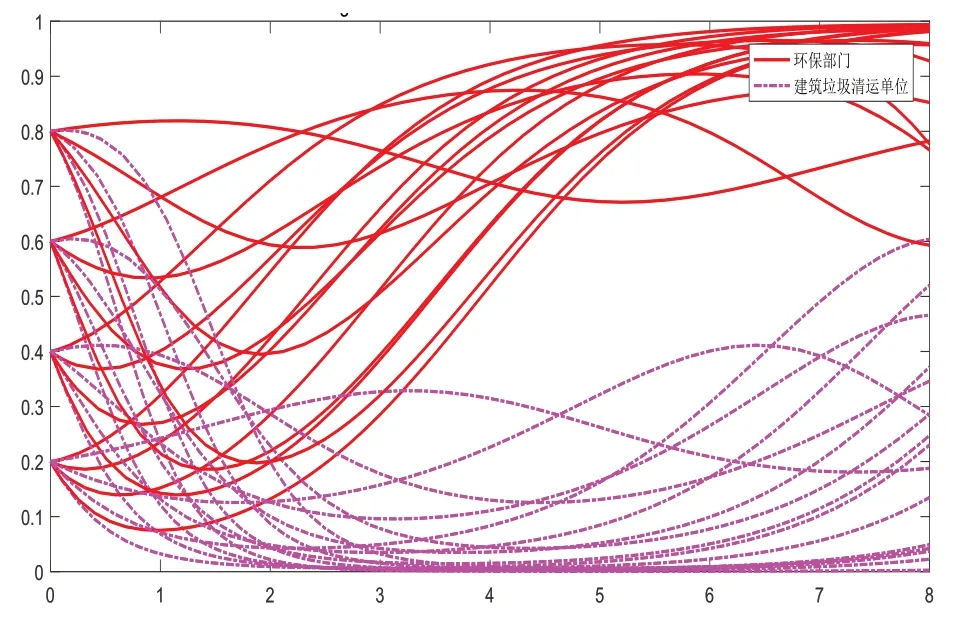
图10 演化稳定点的仿真结果

根据上图所示，此时的博弈双方如推论5所说，处于一种演化的过渡期，此时不存在演化稳定点，政府需要根据特定的社会环境改变当时的政策完善相应的奖惩机制使得现有状态向最优状态（即推论4）的状态转变。

4 结语与建议

本文通过对政府环保部门和建筑垃圾清运单位进行演化博弈分析和仿真，并引入违规罚款、上级嘉奖、建筑垃圾清运单位口碑和周围居民投诉可能性等相关因素，分析结果表明：双方采取的策略与政府环保部门的奖惩机制有着密不可分的关系，当逐渐改变违规罚款、上级嘉奖和单位口碑等条件时，双方选择的策略会不断地改变，特别是当主要因素违规罚款的不断提高时，双方的博弈策略会依次出现（宽松管理，不整改）、（严格管理，不整改）、（严格管理，整改）、（宽松管理，整改）的情况。由上文可知，最满意和最适合社会环境的情况是第四种情况（宽松管理，整改），为了保证达到和维持这一情况，根据上文的博弈模型条件在此提出相关建议：

（1）在地方政府出现清运建筑垃圾违规的情况时，需要政府上级部门乃至中央加强政策的制定和实施，并完善对政策严格执行的下级部门的激励措施，比如增加严格治理下级的财政拨款或者把治理结果当做是晋升条件考核绩效。在这种条件下，能够很大程度上激励下级环保部门改变现有的宽松管理的模式，严格执行现有规章制度并加强监管的力度，促进建筑垃圾清运单位自觉整改，争取提早进入整体效益最优阶段，减少上级政府和环保部门的投入压力。

（2）政府环保部门加大现有的建筑垃圾清运的相关违规惩罚措施，特别是要提高相关违规罚款金额，使得此时进行主动整改的建筑垃圾清运单位的收益远远大于不整改的收益，相关的建筑垃圾清运单位为了保证自身利益，会选择对自己更有利的策略，也就是主动进行整改。当处于最优阶段时，政府环保部门也要保证一定的罚款数额和主动整改相关单位的推广度，维持现有状态，避免现有阶段出现退化的情况。

（3）加强对主动整改的建筑垃圾清运单位的奖励和推广，颁发相关资质证明和荣誉证书，并在相关政府网站进行表彰，提高相关单位的知名度。也可以把相关合法资质和荣誉作为其他政府项目和高投资项目的承包标准，把不整改企业限制在评标的门口，提高主动整改单位的承包项目的数量和质量，也可以间接增加相关单位的收益，使得这些模范企业做好带头作用，带动整体行业的整改氛围。