超声波燃气表矩形流道的雷诺修正系数仿真研究

何明昊, 杨 鸣

超声波燃气表矩形流道的雷诺修正系数仿真研究

何明昊, 杨 鸣*

（宁波大学 信息科学与工程学院, 浙江 宁波 315211）

在超声波流量计测量技术中, 雷诺修正系数相关的研究对于提高计量精度有重要作用. 为研究矩形流道的雷诺修正系数与雷诺数的关系, 对矩形流道在常温常压流量较小情况下进行仿真, 结果发现: 矩形流道层流状态下的雷诺修正系数与雷诺数呈线性相关. 保持压强、体积流量不变, 在不同温度下进行仿真及拟合, 结果表明: 在不同温度下雷诺修正系数与雷诺数的线性关系依然满足. 在上述实验基础上, 对矩形流道湍流状态下的雷诺修正系数与雷诺数关系进行研究, 通过改变温度、压强和体积流量进行仿真及拟合发现, 矩形流道湍流状态下雷诺修正系数与雷诺数呈非线性相关.

超声波燃气表; 矩形流道; 雷诺数; 雷诺修正系数

近年来, 超声波燃气表的发展十分迅速. 相较于传统的燃气表, 超声波燃气表具有测量精度高、压损小、量程比大、适用气体范围广等优点[1]. 过去超声波燃气表以圆形流道为主. 近几年, 日本松下公司率先将矩形流道应用于家用超声波燃气表中, 随后我国杭州威星、辽宁思凯等国内燃气表公司也开始研发矩形流道产品, 目前矩形流道已被大量应用于超声波燃气表. 因此, 如何提升矩形流道下燃气表的测量精度是超声波燃气表研发的关键. 雷诺修正系数是超声波燃气表中一种与流量测量精度相关的补偿系数, 对提升流量测量精度有关键作用[2-3]. 但目前国内外关于矩形流道雷诺修正系数的研究仍较为鲜见.

本文基于计算流体力学(Computational Fluid Dynamics, CFD)构建矩形流道模型, 通过CFD模拟仿真与拟合分析相结合, 研究矩形流道层流状态下雷诺修正系数与雷诺数关系、温度对矩形流道层流状态下的雷诺修正系数与雷诺数关系的影响, 以及矩形流道湍流状态下的雷诺修正系数与雷诺数关系, 以期为提高矩形流道燃气表的流量测量精度提供参考.

1 超声波流量计原理

现阶段超声波燃气表的流速测量方法以时差法为主, 在流道上下游分别安装超声波换能器, 以发射和接收换能器之间的连线作为超声波信号传播路径[4-5]. 图1为时差法超声波燃气表测量原理.

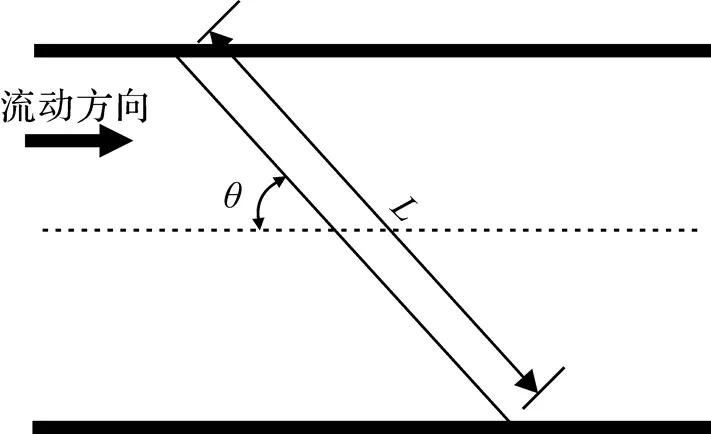
图1 时差法超声波燃气表测量原理

超声波信号在顺流方向传播时间up、在逆流方向传播时间dn的计算公式分别为:

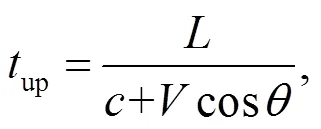
2 矩形流道模型设置

在超声波燃气表的流量计量中, 上下游超声波换能器之间的对应区域即为声道区域, 流体在此声道区域中流动. 而圆形流道的管径较大, 声波覆盖面较小, 导致测量结果有偏差, 因此选用矩形流道, 流道狭窄, 声波能覆盖整个模型宽度, 可以更加准确地测量流体的流量.

通过建模软件Creo 2.0建立矩形流道模型, 如图2所示. 矩形流道截面长12mm、宽50mm, 流道长度100mm, 隔板厚度0.3mm, 隔板与隔板、隔板与流道壁间隔均为2.775mm. 在圆形流道中, 通过安装流速分布器对流体进行整流, 可使流体分布更加均匀, 更适合测量. 而矩形流道尺寸较小,无法安装流速分布器, 因此需要在其中安装等间距隔板以达到整流效果[6].

图2 矩形流道模型

雷诺数()的大小决定了流体的流动状态与流速分布[7]. 当小于2300时, 流体为层流状态; 当大于4000时, 流体为湍流状态; 当介于两者之间时, 为过渡状态, 一般作为湍流状态处理.计算公式为:

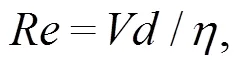
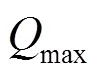
从图3可知, 矩形流道中气体流速分布均匀, 在隔板所划分的局部流道内气体均为层流状态, 隔板能够实现整流. 但对矩形流道应考虑中间部分流速的影响, 因此在模型线平面流道中间设置4段连线作为分割段(图4).

图3 矩形流道流速分布

图4 矩形流道分割段

计算流体力学是流体力学与计算机的结合, 以计算机为工具, 对流体力学中非理想情况进行模拟仿真, 其结果能够直观有效地反映流体的流动状态[10-11]. 研究雷诺修正系数需要结合流体的流动状态, 而实际流量标定装置并不能直观地反映流道内流体的流动状态[12].

在对上述矩形流道设置基础上进行模拟仿真. 将模型导入FloEFD仿真软件, 边界条件为温度20℃、压强10kPa、入口体积流量6.00m3·h-1, 得到4个分割段上的流速分布(图5).

图5 体积流量6.00 m3·h-1时流速分布

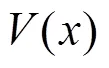
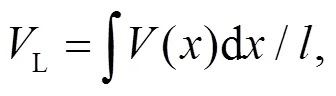
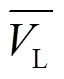
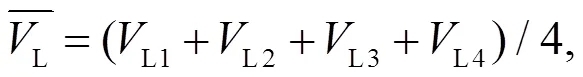
式中:L1、L2、L3、L4分别为4个分割段根据式(6)计算得到的每个分割段上的线平均流速.

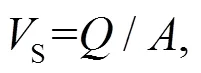
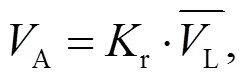
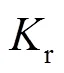
3 拟合分析

3.1 矩形流道层流状态下雷诺修正系数

当小于2300时, 流道中气体为层流状态, 如图6所示, 气体流动平稳, 流速分布均匀.

图6 矩形流道在层流状态下的流速分布

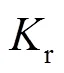
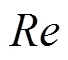
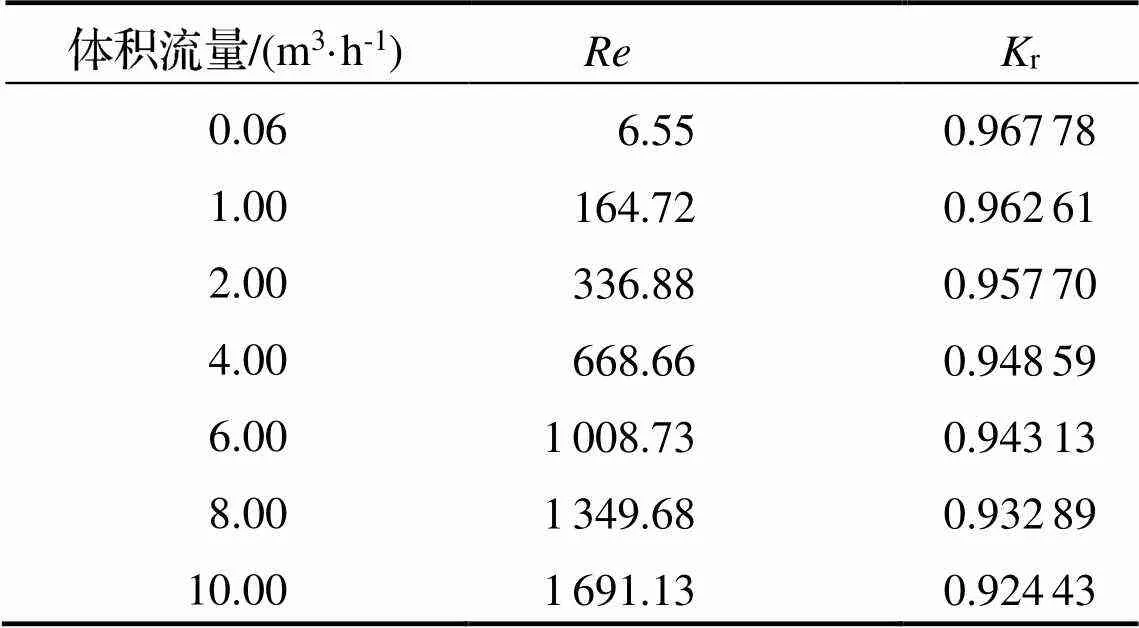
表1 20℃、10kPa条件下Re与Kr值

从表1可知, 当体积流量处于最大值10.00 m3·h-1以下时,均小于2300, 气体处于层流状态. 通过最小二乘法拟合得出矩形流道在20℃、10kPa条件下r与关系(图7).

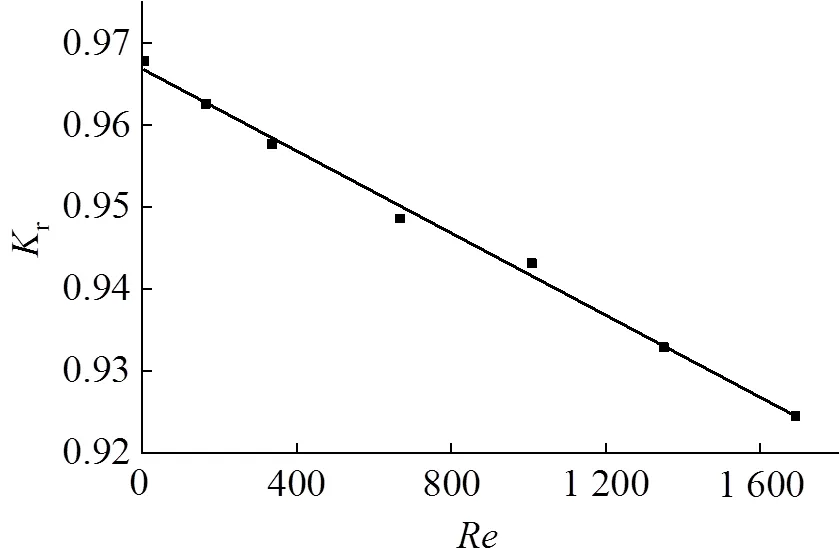
图7 层流状态下Kr与Re关系

由图7拟合结果可知,r与关系为:

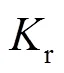
3.2 矩形流道层流状态下对温度的适应性

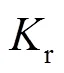
表2 不同温度条件下面平均流速的相对误差 %

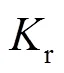
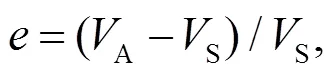
根据式(10)计算得出矩形流道在不同温度条件下不同流量时值(表2).

从图9可知, 在-20~60℃温度条件下矩形流道相对误差满足测量标准. 随着矩形流道内体积流量增加, 在0.06~4.00m3·h-1范围内, 不同温度下相对误差曲线皆呈上升趋势, 在4.00~10.00m3·h-1范围内皆呈下降趋势, 而在不同温度条件下相对误差曲线的幅值不同, 表明温度对矩形流道层流状态下r与关系的相对误差曲线幅值存在影响.

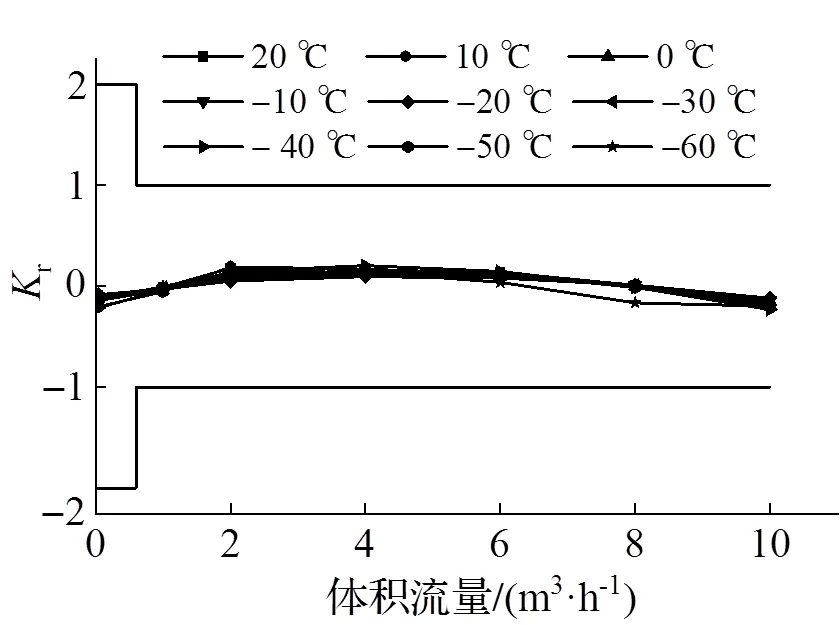
图9 矩形流道在不同温度条件下的相对误差曲线

3.3 矩形流道湍流状态下分析

当大于4000时, 气体在流道中为湍流状态, 流道中存在小漩涡, 流速分布不均匀(图10).

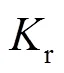
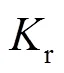
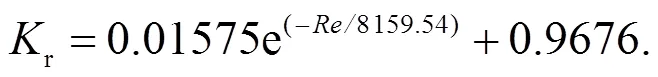
函数图像如图11所示.

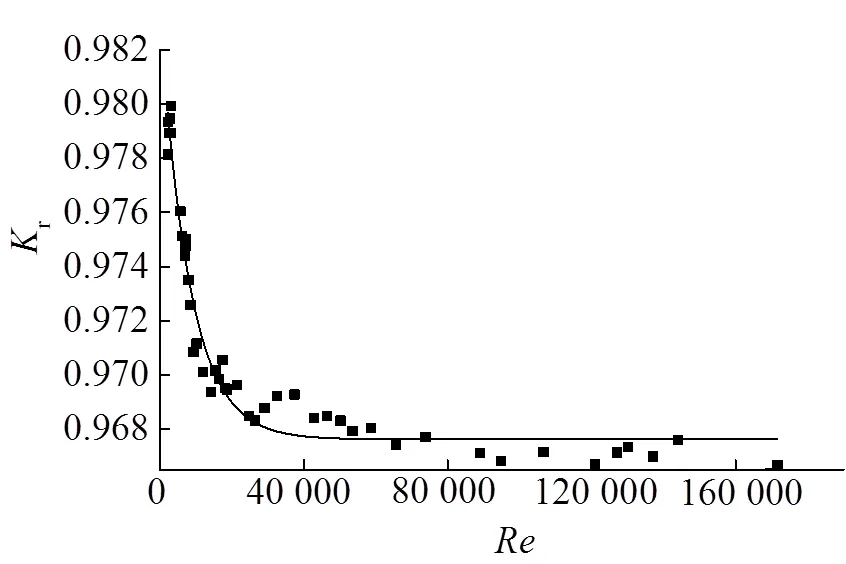
图11 湍流状态下与Re关系曲线

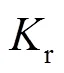
4 结论

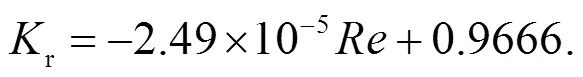
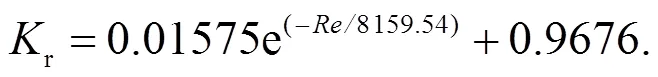
[1] 王雪峰. 基于时差法气体超声波流量计的关键技术研究[D]. 大连: 大连理工大学, 2011.

[2] 汪晓凌, 黄江涛. 改善超声波气体流量计测量精度的方法研究[J]. 轻工科技, 2012, 28(9):124-125.

[3] 唐晓宇, 张宏建, 谢翔, 等. 多声道超声波气体流量计声平面安装角度对测量影响的模型仿真和实验研究[J]. 中南大学学报(自然科学版), 2017, 48(7):1923-1929.

[4] 檀盼龙, 韩思奇. 时差法超声波流量测量技术研究现状与应用[J]. 无线互联科技, 2018, 15(16):31-32.

[5] 杜晓泽, 刘胜祥. 时差法超声波流量计流量系数影响因素分析[J]. 工业计量, 2019, 29(2):14-15; 38.

[6] 陈浩, 杨鸣. 超声波流量计双弯管流场整直问题的研究[J]. 现代科学仪器, 2019(4):5-9.

[7] 孔祥强, 郭璇, 杜广生, 等. 基于CFD的超声波气表结构与流动特性研究[J]. 仪器仪表学报, 2018, 39(9): 220-227.

[8] 孙望, 王鲁海, 王兆杰, 等. 基于PIV测量的超声波流量计内流场特性研究[J]. 实验力学, 2014, 29(6):695- 702.

[9] 林棋, 陈子鑫, 张义勇, 等. 超声波流量计概述及流场数值模拟研究[J]. 石油工业技术监督, 2018, 34(11): 43-47.

[10] 贺胜, 彭黎辉, 仲里敏. 基于CFD的超声波流量计最优声道位置研究[J]. 仪器仪表学报, 2009, 30(4):852- 856.

[11] 王雪峰, 唐祯安. 超声波气体流量计的管道模型仿真和误差分析[J]. 仪器仪表学报, 2009, 30(12):2612- 2618.

[12] Mousavi S F, Hashemabadi S H, Jamali J. Calculation of geometric flow profile correction factor for ultrasonic flow meter using semi-3D simulation technique[J]. Ultrasonics, 2020, 106:106165.

[13] 鲍敏. 影响气体超声波流量计计量精度的主要因素研究[D]. 杭州: 浙江大学, 2004.

[14] 姚平. 复杂流场下气体超声波流量计测量精度提升方法[D]. 杭州: 浙江大学, 2018.

[15] 陈炜刚. 气体超声波流量计非理想流场分析与补偿方法[D]. 杭州: 浙江大学, 2015.

[16] 李跃忠. 多声道超声波气体流量测量关键技术研究[D]. 武汉: 华中科技大学, 2010.

Simulation research on Reynolds correction coefficient of rectangular flow channel of ultrasonic gas meter

HE Minghao, YANG Ming*

( Faculty of Electrical Engineering and Computer Science, Ningbo University, Ningbo 315211, China )

In the measurement technology of ultrasonic flowmeter, the research on the Reynolds correction coefficient plays an important role in improving the measurement accuracy. In order to study the relationship between Reynolds correction coefficient and Reynolds number of the gas in rectangular channel under laminar flow condition, the rectangular flow channel is simulated under the condition of small flow at normal temperature and pressure. Based on the analysis of the fitting results, the conclusion is drawn that the Reynolds correction coefficient of the gas in laminar flow in the rectangular flow channel is linearly related to the Reynolds number. By keeping the pressure and volume flow constant, multiple sets of simulation and fitting experiments are carried out at different temperatures. The results show that the linear correlation between the Reynolds correction coefficient and the Reynolds number is still satisfied at different temperatures. On the basis of the above experiments, the relation between the Reynolds correction coefficient and the Reynolds number of the gas in the rectangular flow channel in the turbulent state is studied. Through simulation and fitting by changing the temperature, pressure and volume flow, it is concluded that the Reynolds correction coefficient of the gas in turbulent flow in the rectangular flow channel is nonlinearly related to the Reynolds number.

ultrasonic gas meter; rectangular flow channel; Reynolds number; Reynolds correction coefficient

TH814

A

1001-5132（2021）02-0025-06

2020−08−15.

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

何明昊（1995－）, 男, 湖北武汉人, 在读硕士研究生, 主要研究方向: 超声波气体流量计. E-mail: 651944260@qq.com

杨鸣（1963－）, 男, 浙江宁波人, 研究员, 主要研究方向: 超声波计量及显微图像处理. E-mail: yangming@nbu.edu.cn

（责任编辑 史小丽）