基于生物智能环状耦合的嵌入式永磁同步直线电机高精度位置协同控制研究
王 璨 李国冲 杨桂林 王冲冲 潘剑飞
(1.深圳大学机电与控制工程学院 深圳 518060 2.中国科学院宁波材料技术与工程研究所 宁波 315201)
0 引言
近年来,多电机协同加工制造日益成为工业的重点,如电路板规模化打孔、多点焊接、联合运输等工业平台中,需要大量的直线协同工序实现既定的高精度协同动作。在传统工业制造系统中,普遍采用旋转电机来实现直线形式的运动,该方式增加了系统结构的复杂度,尤其对于多工位协同加工和运输系统来说,减速齿轮、丝杆、皮带轮等机械部件的引入必然会带来传动误差,难以完成高精度精密协同加工制造的要求。直线电机由于省略了机械转换装置,电机输出直接作用于负载,具有机械故障少、运行寿命长的特点,成为主流运动执行机构[1-3]。在直线电机中,直线永磁同步电机以高推力密度比、高速度等特点,得到学术界和工业界的广泛关注[4-8]。因此,如何在提高单台直线电机控制精度的同时,确保多台直线电机的协同控制精度,是目前多直线电机协同控制的研究重点和难点,具有较好的学术研究和工业应用价值。
为满足工业精密加工指标,多电机协同控制不仅要保证电机间的协同精度,且必须实现单电机本身的高精度跟踪控制。当前,单电机控制普遍采用传统的比例-积分-微分(PID)控制算法,当PID控制器参数设定后,往往无法在线修改,若存在外部干扰,极易降低电机位置跟踪精度。文献[9]提出采用粒子群算法对分数阶PID控制器进行优化,解决了机器人PID控制系统响应慢、输出不稳定的问题;文献[10]利用RBF神经网络对PID控制器参数进行优化。虽然改进后的PID算法在不同程度上解决了传统PID在外部扰动下的控制器参数调整问题,但优化后的PID算法须结合高级算法,计算冗余量大,占用芯片内存大,导致实时性变差。滑模控制(Sliding Mode Control, SMC)对系统参数变化和模型准确程度不敏感,易于硬件和软件实现[11]。因此,SMC具有鲁棒性高和易于实现的特性,适用于永磁同步直线运动控制系统位置控制[12]和推力控制[13]。对于直线电机,基于人体激素调节原理的生物智能控制方案被提出[14],已成功应用于波浪发电[15]和移动机器人等领域[16]。
对于多电机协同控制,控制策略一般分为非耦合和耦合两种[17]。相比于耦合协同控制,非耦合协同控制策略的各子系统间信息传递是单向的,且子系统间信息没有反馈,易导致系统的整体协同精度和抗干扰性能较差。耦合式协同控制策略主要有相邻交叉式耦合控制、偏差式耦合控制和环状式耦合控制三大类[18-19]。
相邻式交叉耦合协同控制的思想是当两电机的输出状态不匹配时,合理设置相邻交叉耦合控制器参数,达到协同控制的效果[20]。但相邻式偏差耦合控制仅限于两个电机之间的误差补偿,当电机个数较多时,相邻式偏差耦合协同控制策略会导致电机间的协同性能下降[21-22]。
偏差式耦合协同控制是在相邻式交叉耦合基础上发展而来的,最早由Perez-Pinal等提出[23]。该方案克服了相邻式交叉耦合不适用于电机数量大于两台的问题,可用于多电机控制。误差补偿是偏差式耦合协同控制的关键,系统中每台电机看作是一个控制轴,将每个轴的信息都传递给偏差耦合式控制器,经偏差耦合算法计算输出每个轴的补偿值。偏差式耦合控制器虽然解决了相邻式偏差耦合控制不适用于电机个数大于两台的情况,但当电机个数过多时,会增加偏差耦合控制器的复杂度。
环状耦合控制是在相邻式偏差耦合和偏差式耦合的基础上进行改进的一种控制策略,既解决了相邻偏差耦合中第一台电机与最后一台电机无法耦合补偿的问题,又简化了偏差耦合控制中控制器数量,当系统中电机数量为n时,系统所需要的控制器数量为2n,大大减少了控制器的个数[23-24]。环状耦合控制策略在调控每台电机与参考信号之间的跟踪误差的同时,也调控该电机与相邻电机之间的误差,系统中任一台电机的输出发生变化,都将对相邻电机造成影响,所有电机两两耦合,形成一个环状结构[21]。耦合环的存在能够保证系统在受到干扰时,仍能保持良好的协同性能。
针对多电机协同加工系统,本文拟构建基于集成永磁同步直线电机(Integrated Permanent Magnet Synchronous Linear Motor, IPMSLM)运动控制平台,结合滑模变结构(Sliding Mode Variable Structure,SMVS)算法与环状耦合协同控制器,在无法精确建模的前提下,提高IPMSLM的系统定位精度。同时,借鉴生物领域激素调节原理,设计一种生物智能控制(Biological Intelligent Control,BIC)算法,进一步提高单台电机高精度定位,并基于Lyapunov稳定性原理设计协同控制算法,实现IPMSLM电机间的高精度协同定位。
1 永磁同步直线电机结构与工作原理
IPMSLM由永磁体定子导轨和多个动子及线圈构成,符合嵌入式多电机的直驱结构。本文研究的IPMSLM结构如图1所示,采用单边平板型,线圈缠绕在硅钢片上构成动子,三个动子在一定范围内独立运动,每个动子与定子导轨为一独立电机,各电机之间的运动不影响其他电机运动状态,且电机各自的磁路相互独立。定子底座由极性相反的永磁体依次交互排列组成,定子底座长为4m。电机主要参数见表1。
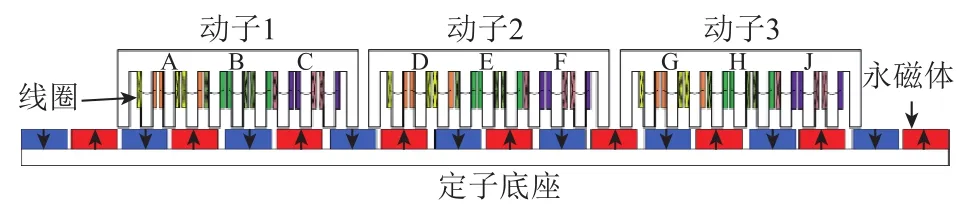
图1 IPMSLM结构Fig.1 IPMSLM structure
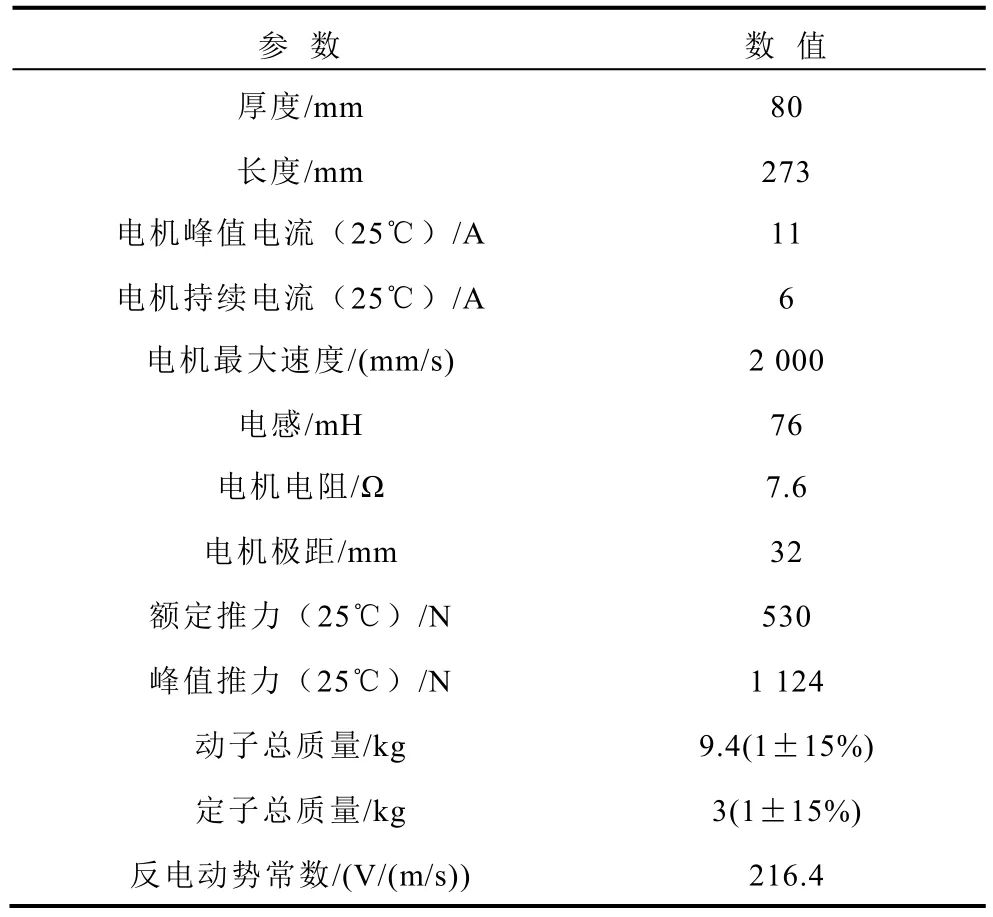
表1 电机参数Tab.1 Motor parameters
PMSLM 由旋转电机发展而来,二者工作原理相同。当给 PMSLM动子线圈注入相位相差 120°的对称交流电时,在动子与定子间形成气隙磁场,气隙中的磁场按照A、B、C三相相序沿直线方向移动,气隙中的磁场被称为行波磁场,行波磁场的运动速度Vs为

式中,ƒ为交流电的频率;τ为电机极距。
通入三相交流电之后,电机输入总功率为
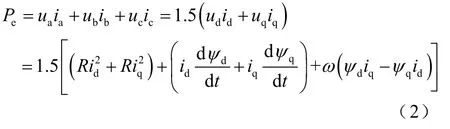
式中,ua、ub、uc和ia、ib、ic分别为三相电压和电流;ud、uq和id、iq分别为d轴、q轴电压和电流;R为d轴、q轴的等效阻值;dψ、qψ分别为d轴、q轴的磁链。总功率Pe由电功率和电磁推力做的功组成,v为电机速度,电磁推力所做的功为机械功,表达式为
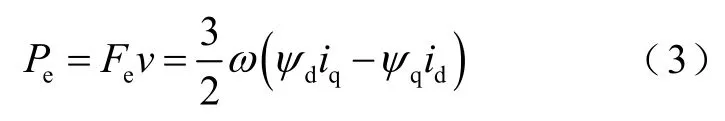
通过式(3)可以得到电机的电磁推力Fe为
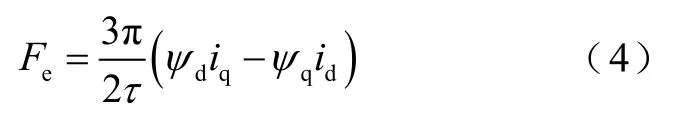
2 基于Lyapunov的BIC-SMVS环状耦合的IPMLSM位置协同控制设计
人体内各种激素的调节都由神经内分泌系统控制,并且这种调节机制是一种良好的自调节机理,神经内分泌是人体内各类激素调节的中枢,调控机理类似于控制论里的反馈调制[25]。人体睾丸性激素反馈调节原理如图2所示,下丘脑根据体内睾酮素(Te)的浓度来调整促性腺激素释放激素(GnRH)的浓度,GnRH的浓度又能进一步影响垂体的活动,促使垂体分泌黄体生成素(LH),LH作用于睾丸使睾丸产生睾酮素(Te)。小丘脑上的睾丸素受体能够检测体内Te的浓度,如果Te的浓度过高,则下丘脑会减少GnRH的生成量,进一步,GnRH的量减少又能使垂体减少LH的产生量,LH分泌量的减少会刺激睾丸减少Te的分泌,所以,到最后体内Te的浓度便会减少并逐渐恢复到正常状态,反之亦然,此类调控机理和自控中的反馈调节类似。
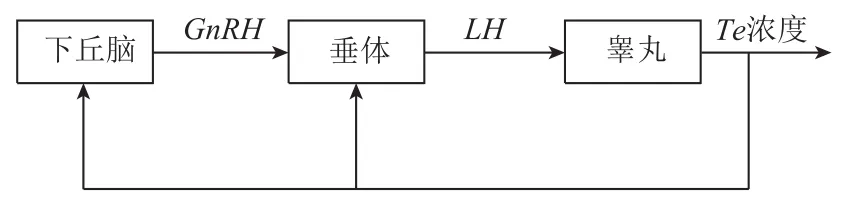
图2 人体睾丸性激素反馈调节原理Fig.2 The principle of feedback regulation of human testicular sex hormones
因此,本文基于人体睾丸性激素反馈调节原理[26]设计BIC生物智能控制算法,如图3所示,应用于单台直线电机,实现高精度位置控制。
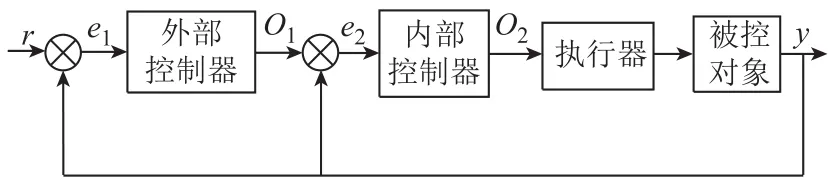
图3 BIC控制结构Fig.3 BIC control structure diagram
在电机控制系统中,BIC控制器的外部控制器采用比例算法,使系统快速调整偏差;BIC控制器的内部控制器采用滑模变结构算法,用来保证系统的鲁棒性能。在实现单台PMSLM高精度位置控制后,基于Lyapunov稳定性原理设计环状耦合位置协同控制器,应用到IPMSLM位置协同控制系统,最终实现高精度多电机协同控制。
2.1 单电机外部控制器设计
外部控制器的目的是当系统输出发生变化时,外部控制器起到快速调节偏差的作用,通过内部控制器调节,使得偏差快速逼近于零。外部控制器的输出信号随着偏差的变化而变化,当系统输出变化量为零时,外部控制器的输出为r,图 3中外部控制器的输出O1为
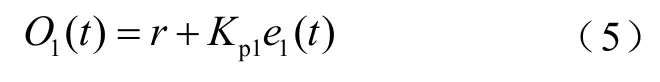
式中,e1(t)为参考值与实际值的差值;Kp1为外部控制器的比例系数。在一定范围内,Kp1的值越大,对输出变化量的调节能力越强,控制效果越明显。当Kp1=0时,外部控制器无法调节偏差;当Kp1过大时,反而会引起系统振荡,系统处于不稳定状态。
2.2 单电机内部控制器设计
内部控制器的目的是进一步减小系统误差,提高鲁棒性能。电机状态空间方程为
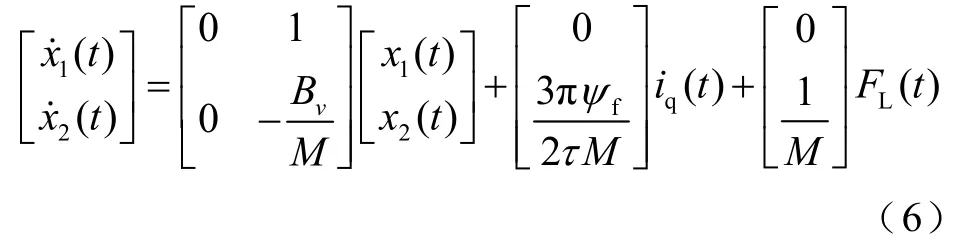
式中,x(k)为系统状态变量,x(k)=[x1(k)x2(k)],x1(k)和x2(k)分别为位置和速度;u(k)为控制变量,u(k)=iq。
由于IPMSLM的端部效应、齿槽效应及强耦合多变量的问题,难以进行精确建模。滑模控制策略不依赖被控对象的精确模型,提高IPMSLM位置控制器的鲁棒性。合理设计趋近律能优化滑模控制的效果,相较于常用的指数趋近律,双幂次趋近律的削弱抖振效果较强,不足之处在于双幂次趋近律控制运行速度偏慢[27]。而双幂次趋近律中加上变指数项,与指数趋近律相比,运行速度更快且抖振削弱能力更强[28]。
因此,本文选用双幂次加变指数项趋近律,即
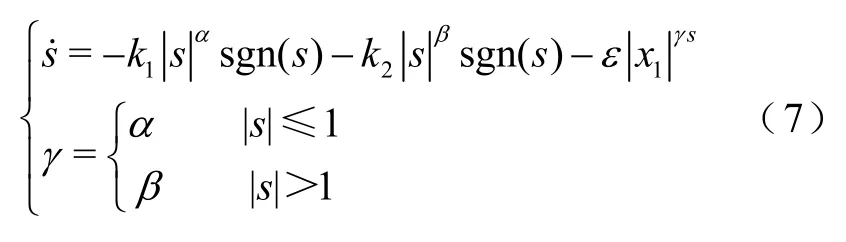
式中,k1>0、k2>0;0<α<1;β>0;sgn(·)为符号函数。
控制目标是在有限时间内通过设计一个连续的具有鲁棒性的滑模算法使得外部控制的输出与位置的差值e2等于电机速度x2,即e2=x2,内部控制器的滑模面为

式中,c为某个正常数。
内部控制器设计为
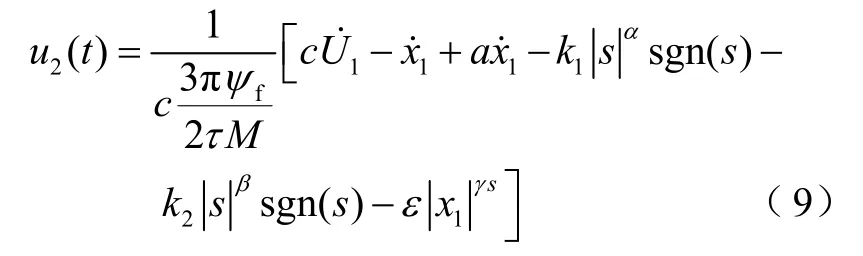
为进一步削弱抖振,将上述符号函数替换成饱和函数为

式中,c、k1、k2、α、β、ε和饱和函数中的δ为待定参数。
2.3 基于Lyapunov的多电机环状耦合位置协同控制器设计
被控对象的跟踪误差可以表达为
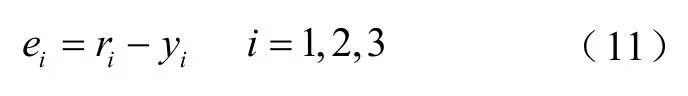
式中,ri为电机的位置参考指令;ei为被控对象中第i台电机的位置跟踪误差;yi为被控对象中第i台电机的实际位置。
电机i与电机i+1之间的误差表示为
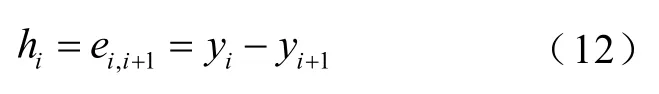
式中,yi为第i台电机的实际位置;yi+1为第i+1台电机的实际位置。在IPMSLM位置协同控制系统中,不仅保证ei→0,还要使hi→0成立。
传统环状耦合控制策略普遍基于PID控制算法,其协同控制器为

式中,Eo为协同控制器输出;Kp、Kd、Ki为基于PID环状耦合控制器的参数。
传统基于 PID环状耦合控制策略虽然易于实现,但抗干扰能力差,难以实现高精度控制的要求,因此,本节基于Lyapunov稳定性原理设计协同控制策略。
第i台电机经过环状耦合控制器修正之后的跟踪误差为

式中,Ki为正常数。
此处以系统中第一台电机为例,如果Ei→0,则Lyapunov函数可定义为

如果∃E1=-c1E1(c1>0)满足,则有
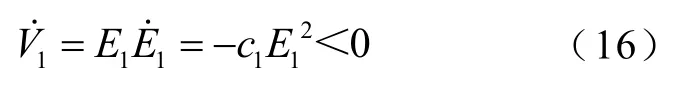
因此,当满足条件E1→0时,系统是全局渐近稳定的。
将式(11)和式(12)代入式(14)中得到
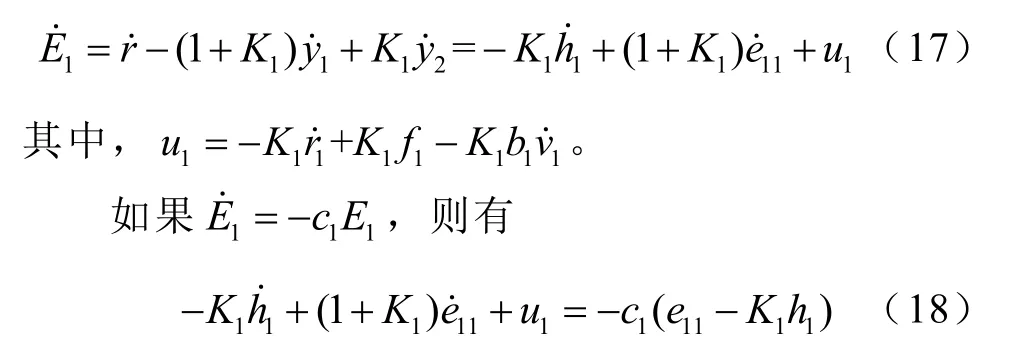
因此,控制率u1可以表示为

与此同时,E1→0成立。同理,存在其他电机控制率ui,使得Ei→0成立。
3 IPMSLM位置协同控制实验
本文利用 RT-Lab快速开发平台搭建半实物仿真平台,实现IPMSLM位置控制算法,结合IPMSLM实物平台,开展单电机跟踪和多电机协同的位置控制实验。实验条件是在幅值为30mm,频率为0.2Hz的方波信号(标称状态)作用下,分别进行空载和变负载实验。变负载通过弹簧实现,弹性系数为3N/mm。单台电机的PID控制器参数根据实时在线实验调试,确定位置环PID控制器的Kp=12,Ki=0,Kd=0.02,速度环 PID 控制器的Kp=20,Ki=0.08,Kd=0,而基于 PID环状耦合协同控制器的参数Kp1=2.2,Ki1=0,Kd1=0,Kp2=2.0,Ki2=0,Kd2=0,Kp3=1.8,Ki3=0,Kd3=0。内部滑模控制器参数根据电流最小误差标准,得到c=1 050,k1=0.001,k2=0.001 5,α=0.7,β=1.35,ε=0.000 1,δ=1.5,外部控制K=15,以上参数在标称状态下得到,使系统稳态误差最小,固定上述参数不变进行实验。

图4 实验平台Fig.4 Experimental platform
3.1 基于BIC-SMVS的单台电机控制
当空载条件下,单台直线电机PID控制和BICSMVS控制作对比,实验结果如图5所示。
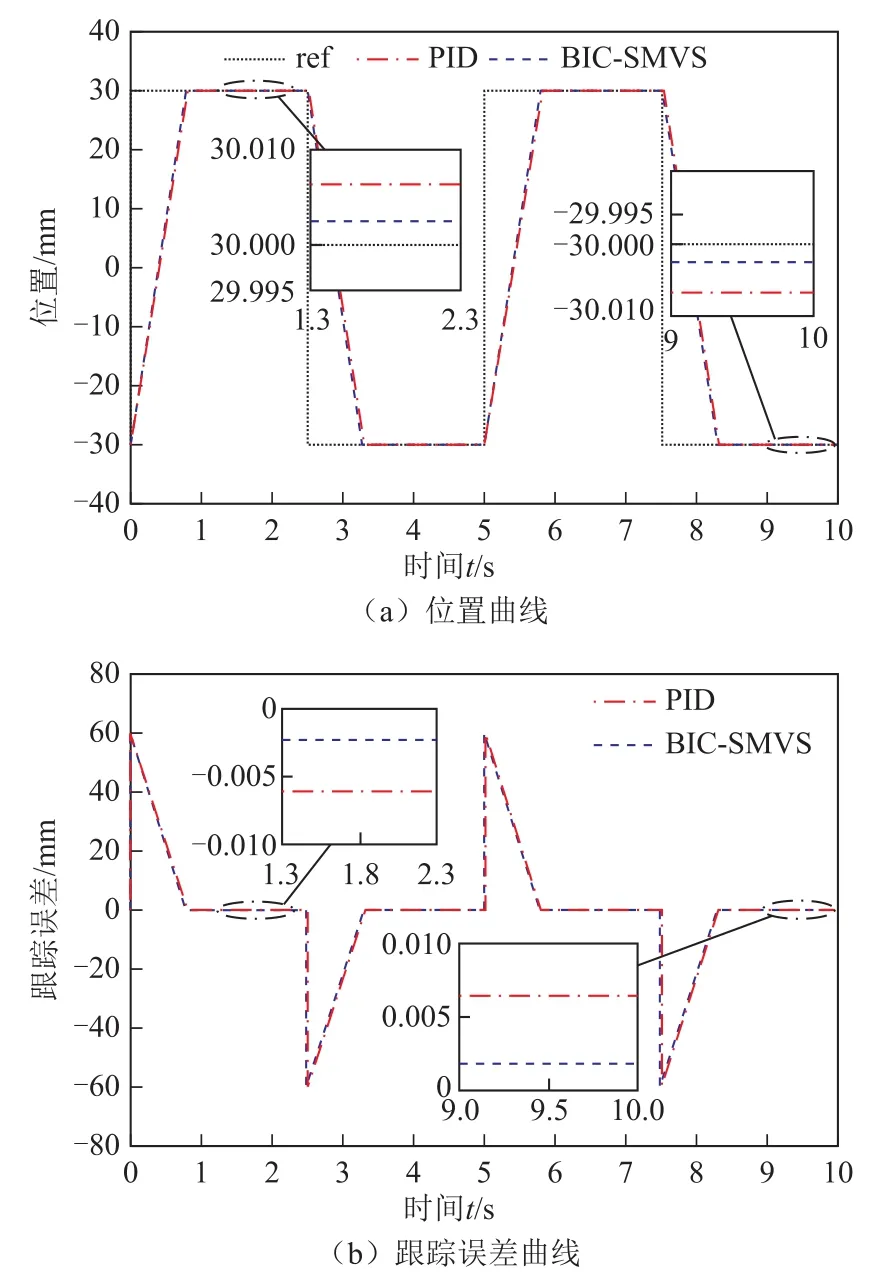
图5 空载下单台电机位置控制Fig.5 Experimental results o f single motor position control under no load
在变负载条件下,单台电机的PID控制和BICSMVS控制作对比,实验结果如图6所示。

图6 变负载下单台电机位置控制实验结果Fig.6 Experimental results of Single motor position control under variable load
由图5和图6看出,在空载条件下,基于BICSMVS控制的跟踪误差在±3µm内,而 PID控制为±6µm。在变负载条件下,基于BIC-SMVS控制的跟踪误差在±4µm内,而PID控制在±9µm内,因此,对单电机控制,本文基于 BIC-SMVS的控制方法,在空载和变负载条件下,稳态位置控制精度均优于传统PID控制。
3.2 基于Lyapunov的BIC-SMVS环状耦合的多电机协同控制
当空载条件下,使用基于PID环状耦合协同控制和基于Lyapunov的BIC-SMVS环状耦合协同控制进行实验对比,实验结果如图7和图8所示。

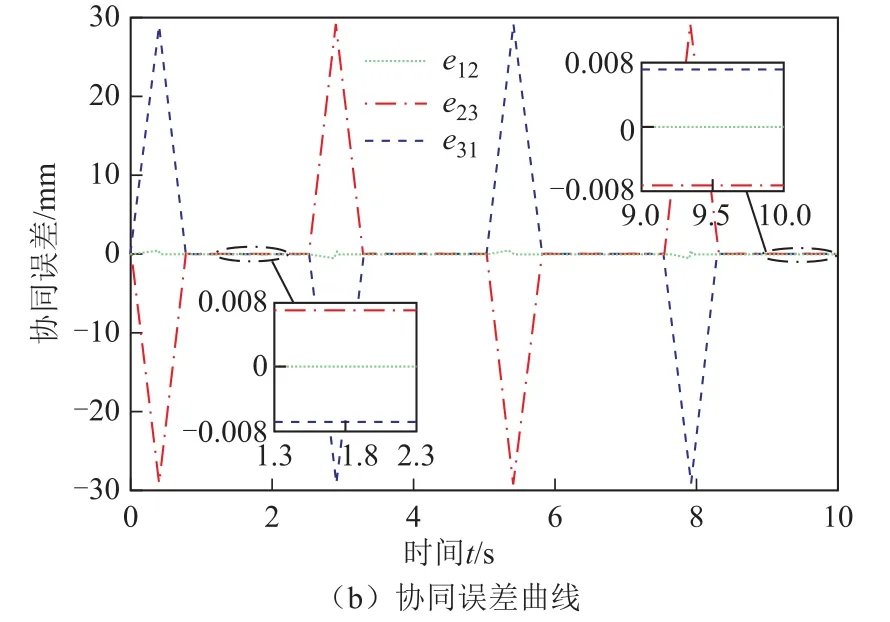
图7 空载条件下基于PID环状耦合算法的IPMSLM位置协同控制Fig.7 IPMSLM position cooperative control based on PID loop coupling algorithm under no load
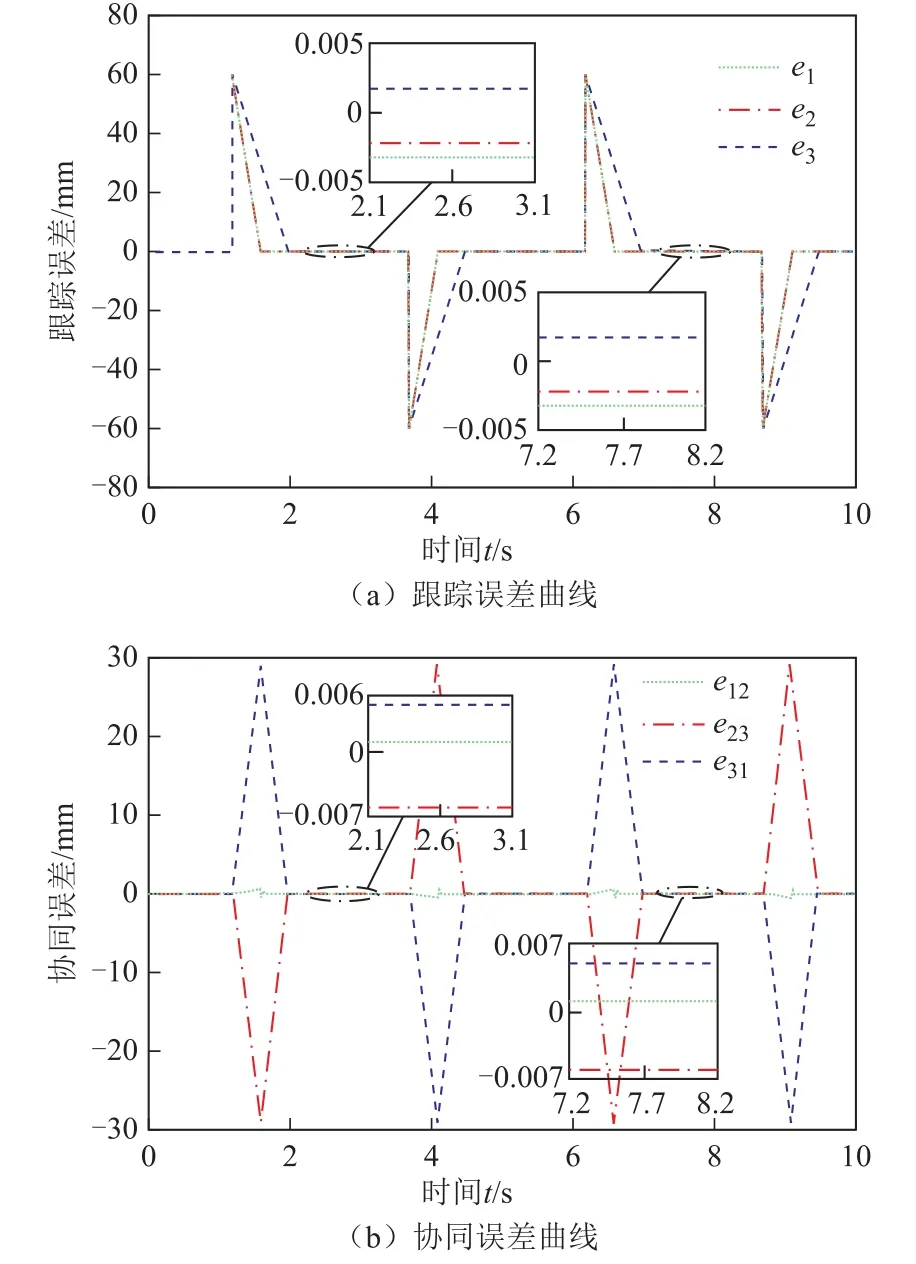
图8 空载条件下基于Lyapunov的BIC-SMVS环状耦合算法的IPMSLM位置协同控制Fig.8 IPMSLM coordinated position control based on BIC-SMVS loop coupling algorithm under no load
图7和图8基于PID环状耦合协同控制算法的跟踪误差在±6µm内,协同误差在±8µm内。而基于Lyapunov的 BIC-SMVS环状耦合协同控制算法的跟踪误差在±3µm内,协同误差在±6µm内。
当变负载条件下,使用PID环状耦合协同控制和基于 Lyapunov的BIC-SMVS环状耦合协同控制作实验对比,实验结果如图9和图10所示。
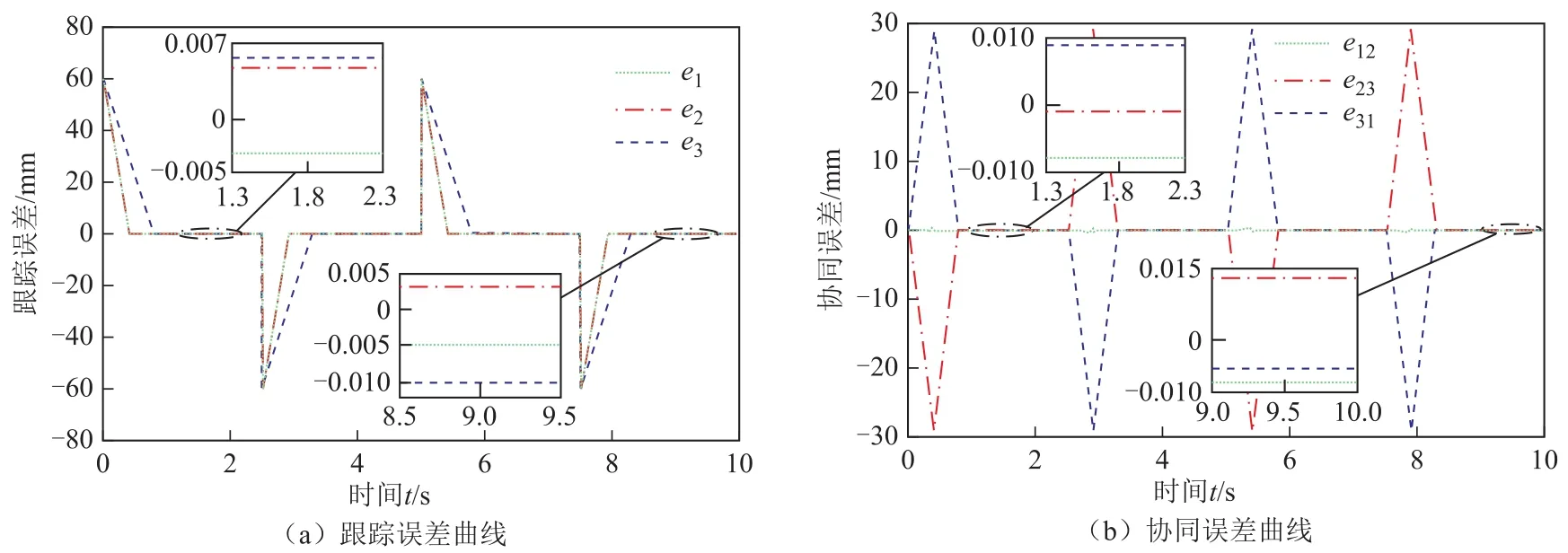
图9 变负载条件下基于PID环状耦合算法的IPMSLM位置协同控制Fig.9 IPMSLM position collaborative control based on PID loop coupling algorithm under variable load
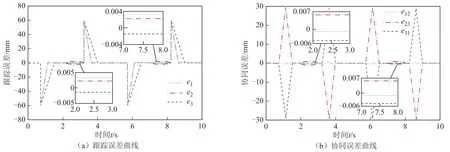
图10 变负载条件下基于Lyapunov的BIC-SMVC环状耦合算法的IPMSLM位置协同控制Fig.10 IPMSLM position cooperative control based on BIC-SMVC ring coupling algorithm under variable load
由图9和图10可知,基于PID环状耦合协同控制算法的定位误差在±10µm 内,协同误差在±15µm。而基于 Lyapunov的 BIC-SMVS环状耦合协同控制算法的定位误差在±4µm 内,协同误差在±6µm 内。
因此,通过分别进行空载和变负载实验,相比于传统的基于PID环状耦合协同控制算法,本文提出的基于Lyapunov的BIC-SMVS环状耦合协同控制算法的跟踪误差和协同误差均有提高,在实验条件改变下,效果保持一致,实现了高精度协同定位的目标。
4 结论
本文借鉴生物学人体激素调节原理,设计一种适用于 IPMSLM的BIC-SMVS位置控制器。BICSMVS算法包含内外两个控制器,外部控制器起到快速调节的作用,提升系统的快速响应性能,内部控制器进一步减小误差并提高系统的鲁棒性。同时,针对 IPMSLM协同运动时会产生同轴共振的问题及外部扰动导致的系统整体协同精度较低的问题,设计一种基于Lyapunov的环状耦合协同控制算法。实验结果表明,采用基于Lyapunov的BICSMVS环状耦合协同控制算法后,单电机定位精度在±4µm以内,系统协同定位精度在±6μm以内。设计的位置控制算法在保证单台电机高精度定位的基础上,进一步实现了 IPMSLM高精度协同定位控制。

