吉林市暴雨强度公式推求和设计雨型

邱译萱，任晓峰， 杨雪艳， 姜忠宝， 李宇凡

(1.吉林省气候中心,长白山气象与气候变化吉林省重点实验室，吉林 长春 130062；2.吉林省吉林市气象局，吉林 吉林 132013)

引 言

目前全球变暖趋势仍在进一步持续，在气候变暖背景下极端降水事件更加严重和频繁[1]。自20世纪60年代以来，中国极端降水频次呈增多趋势[2]，至21世纪末中国极端降水事件强度仍将增强、频率仍将增多，暴雨洪涝风险逐渐加大[3]。短历时强降雨是诱发城市洪涝的直接因素，造成交通中断、电力故障、城市污染等问题，严重威胁国民经济和人民群众生命财产安全[4]。吉林市是吉林省第二大城市，地形属于低山丘陵，因松花江干流流经吉林市区，水资源丰富，对防汛要求较高。吉林市近10 a来发生暴雨16次，其中2010年和2017年的暴雨降水量大、时段集中，造成严重洪涝灾害，带来了巨大损失[5]。加快提高城市防洪排涝能力，保证城市排水管网安全，已成为当前城市水利规划工作亟待解决的问题。

暴雨强度公式及暴雨雨型是城市排水标准计算、城市规划设计等工作的基础[6]，其可靠性关乎城市的安全。我国雨水流量设计计算普遍采用的是1987年修订的《室外排水设计规范》[7](GBJ14-87)规定的推理公式，该版公式较为陈旧，已无法满足当前现实需要，从科学角度考量，应根据最新的统计资料进行完善修编。近年来，国内外对城市暴雨强度公式和设计雨型的相关研究主要集中在暴雨样本筛选、频率拟合方法及雨型模型的选取。筛选暴雨样本常用的方法主要有年最大值法和年多个样法[8-12]，基于这两种方法的重现期对应转换关系已有相关研究[13-15]。随着国内城市降雨资料观测年限的增加，年最大值法选取的样本独立性增强，且在数据收集和统计上相对容易，应用最为广泛。目前较为流行的频率拟合方法为理论频率曲线适线法，即对实测暴雨样本进行适线调整，得出重现期(P)、降雨强度(i)和降雨历时(t)三者的经验数据表，以此为基础计算暴雨强度公式。一般常用的频率分布曲线包括P-Ⅲ型、Gumbel型、指数型和对数正态分布曲线[16-18]。ALHASSOUN[19]在估算利雅得地区的降雨强度公式时，对P-Ⅲ型、Gumbel型和对数正态分布曲线3种频率拟合方法进行了对比，认为理论频率曲线对暴雨样本拟合效果最好的，计算得到的暴雨强度公式不一定精度最高。因此在计算暴雨强度公式时，需要综合考虑选样方法、当地实际暴雨分布规律、频率曲线误差和公式误差来确定最适宜的暴雨强度频率曲线。暴雨雨型反映了暴雨过程在时间尺度上的分布变化，常用的雨型有芝加哥雨型、Huff雨型、Pilgrim & Cordery雨型、三角形雨型、均匀雨型、同频率分析方法雨型等[20-23]。其中芝加哥雨型的雨强过程线的计算方法相对简单，同时雨峰位置系数可以根据暴雨强度公式计算得出，因此在相关研究中应用较多。

因极端降水事件特征不断变化，本研究利用1961—2017年的逐分钟降雨量资料重新计算吉林市暴雨强度公式，并首次进行短历时雨型设计，对吉林市当前暴雨特性进行研究，以期为城市排水系统设计及海绵城市规划[24]提供参考。

1 资料与方法

1.1 资料来源及合理性分析

以吉林市城郊气象站1961—2017年逐分钟降雨量为基础数据，其中1961—2004年分钟降雨数据为降水自记纸记录经数字化处理及人工审核或修正后得到的资料；2005—2017年分钟降雨数据从自动站资料中获取。资料均来自吉林省气象档案馆。

吉林市城郊气象站为吉林市区仅有的1个国家级气象观测站，具有长期降水观测。1961—2017年，吉林市城郊气象站经历两次迁站，观测场海拔由2003年第一次迁站前的184.1 m变为198.5 m，2013年第二次迁站海拔变为198.8 m，与市区平均海拔接近，具有区域代表性。对逐年降雨量资料采用标准正态方法(SNHT)进行迁站前后时段的显著性检验(显著性水平0.05)，检验结果均不显著，说明迁站前后的降水资料具有良好的完整性和均一性。

1.2 方 法

1.2.1 暴雨样本序列建立及选择

采用逐分钟滑动统计法，按照“不漏场次、不漏大值”的原则，挑取5、10、15、20、30、45、60、90、120、150、180 min共11个历时的所有场次降雨数据。

年最大值法：选取逐年各历时最大雨量，各历时样本数为57个，作为建立短历时暴雨强度公式的统计样本。

年多个样法：将逐年各历时前8场最大雨量(各历时基础样本数为57×8=456个)从大到小进行排序，并按从大到小选择资料年份的4倍(各历时最终样本数为57×4=228个)数据，作为统计样本。

1.2.2 短历时强降水变化极值及均值

(1) 短历时强降水的极值

将各历时以年最大值法选取的统计样本从大到小进行排序，选取最大的10个降水极值，将资料年份均分为前后两段，通过统计前后两个时段的降水极值样本数，分析短历时强降水的极值分布特征。

(2) 短历时强降水的均值

统计各历时每年10场最大雨量，对比不同年代的多年暴雨量平均值，分析短历时强降水的均值分布特征。

1.2.3 暴雨强度公式

(1) 样本频率和重现期计算及理论频率分布曲线拟合

将统计样本按照降序排列，计算样本的经验频率，重现期P与经验频率p互为倒数。p计算公式如下：

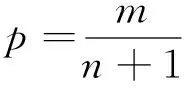
(1)

式中：m为样本排序数；n为样本总数。

基于选取的统计样本，采用理论频率曲线对样本的经验频率数据序列进行趋势性拟合，根据暴雨强度公式的重现期重点关注区间(2～20 a)和范围要求(2～100 a)[25]，对频率分布曲线进行适线调整和外延。

从P-Ⅲ型、Gumbel型和指数型3种分布曲线中，选取拟合效果较好的理论频率曲线进行暴雨强度公式拟合。

P-Ⅲ型分布即伽玛分布，其概率密度函数如下：

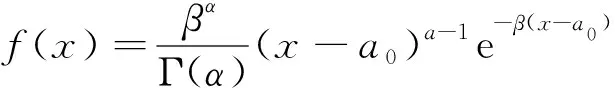
(2)

式中：α、β和a0为P-Ⅲ型分布包含的参数；Г(α)为α的伽马函数。

Gumbel型分布又称为极值Ⅰ分布，其概率密度函数如下：

f(x)=aexp(-y-e-y)

(3)

式中：y=a(x-b)，a为分布的尺度参数，b为分布的位置参数。

指数型分布概率密度函数如下：

f(x)=ae-a(x-a0)

(4)

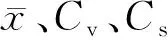
(2)暴雨强度公式拟合

依据《室外排水设计规范》[26](简称《规范》)，暴雨强度公式如下：

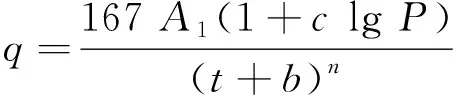
(5)

式中：q[L·(s·hm2)-1]为暴雨强度；P(a)为重现期；t(min)为降雨历时；A1为雨力参数；c为雨力变动参数；b为降雨历时校正参数；n为暴雨衰减指数，与重现期有关。

由3种理论频率分布曲线确定P-i-t三联表，采用最小二乘法计算参数，得到暴雨强度公式。

(3)精度检验

精度检验重点为重现期2～20 a[25]，在雨强一般的地区，暴雨强度平均绝对均方根误差σR均不宜超过0.05 mm·min-1，在雨强较大的地区，平均相对均方根误差σq均不宜超过5%。

平均绝对均方根误差：

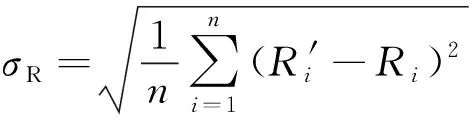
(6)

平均相对均方根误差：

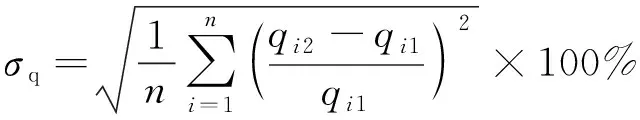
(7)

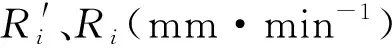
1.2.4 新、旧版暴雨强度公式对比

(1)时段暴雨量极值与均值对比

在两版公式对应资料年限内，统计各历时暴雨量极大值，分析极值差异；统计各历时每年10场最大雨量，求取多年平均值，分析均值差异。

(2)暴雨强度值变化率分析

对两版公式计算的暴雨强度值变化率进行分析，其计算公式如下：

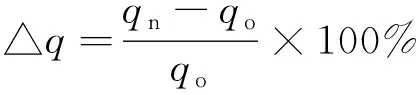
(8)

式中：Δq为变化率；qn和qo分别为新、旧公式计算的雨强。

1.2.5 芝加哥法设计雨型

(1)建立样本序列。挑取30、60、90、120、150、180 min共6个历时的所有场次降雨数据，记录每个过程的起止时间及过程内逐分钟雨量值、累计雨量值，将各历时的过程累计雨量值从大到小进行排序，选择大约的资料年份数(各历时样本数约为57个)的数据，作为统计样本。将过程累计雨量最小值，作为该历时的暴雨雨量阈值。

(2)雨峰位置系数将确定的各历时统计样本以5 min间隔为步长，滑动计算5 min降水量，挑出各样本雨量最大的时刻，记为雨峰位置，雨峰位置出现时间除以该样本历时，得到雨峰位置系数；计算各样本雨峰位置系数的平均值，得到各历时的雨峰位置系数。以历时为权重，对各历时的雨峰位置系数求平均，得到芝加哥雨型的综合雨峰位置系数。

(3)芝加哥降雨过程线模型确定

结合1.2.3中计算得到的新公式参数，计算雨峰前、后瞬时降雨强度。计算公式如下：

雨峰发生前(上升段)：

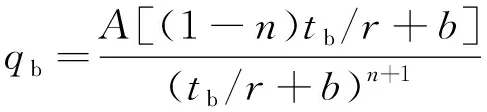
(9)

雨峰发生后(下降段)：

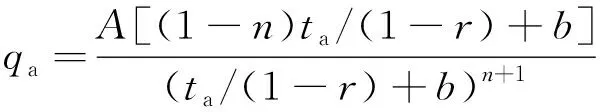
(10)

式中：qb和qa(mm·min-1)分别为峰前、峰后的瞬时暴雨强度；r为综合雨峰位置系数；tb和ta(min)分别为雨峰上升段和下降段的时间；A、n和b均为暴雨强度公式中的参数，其中A=167A1(1+clgP)。由qa，qb计算芝加哥降雨过程线每5 min的平均降雨强度、平均降雨量和累计降雨量，确定短历时雨型。

2 短历时强降水变化特征

2.1 极值分布特征

将资料时段分为1961—1987年、1988—2017年两个时段，对比各历时暴雨样本在两个时段内的样本数(表1)。5～60 min和180 min历时的暴雨样本数1961—1987年与1988—2017年相同或略少， 90～150 min历时的样本数1961—1987年明显少于1988—2017年。

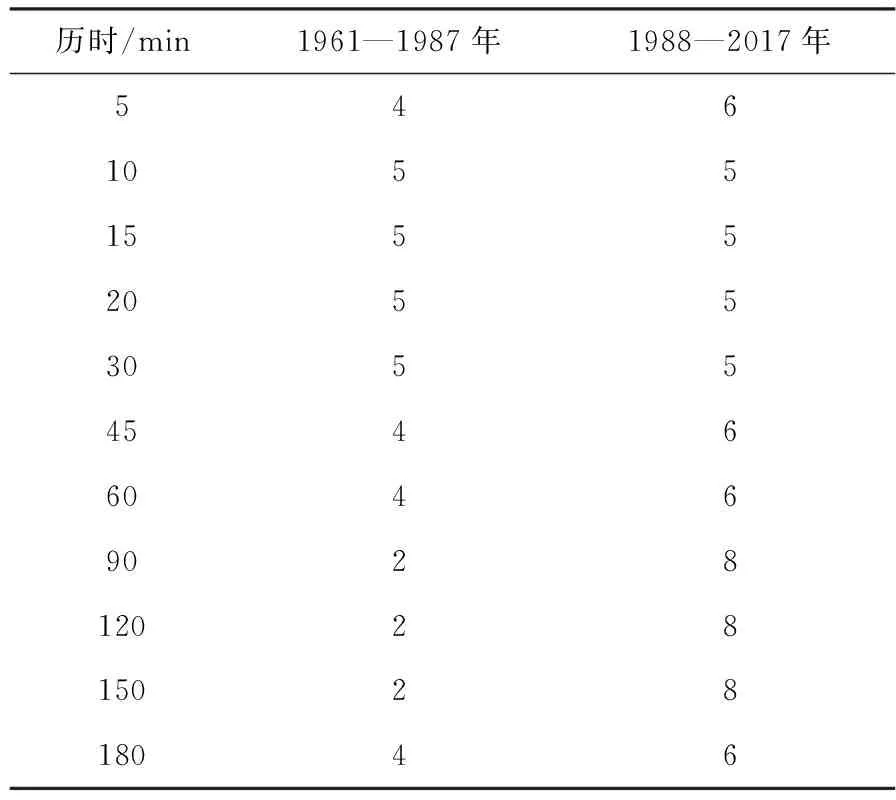
表1 吉林市1961—1987年和1988—2017年两个时段各历时暴雨样本数Tab.1 The sample sizes of rainstorm with different duration during 1961-1987 and 1988-2017 in Jinlin City

2.2 均值分布特征

图1为吉林市各历时不同年代平均暴雨雨量。可以看出，各历时暴雨量平均值变化规律一致，均呈波动性上升趋势， 1990年代和2010年代为暴雨量均值较高时段。年代波动也随降雨历时的延长而加大，5 min历时暴雨量平均值的年代变化明显较小。

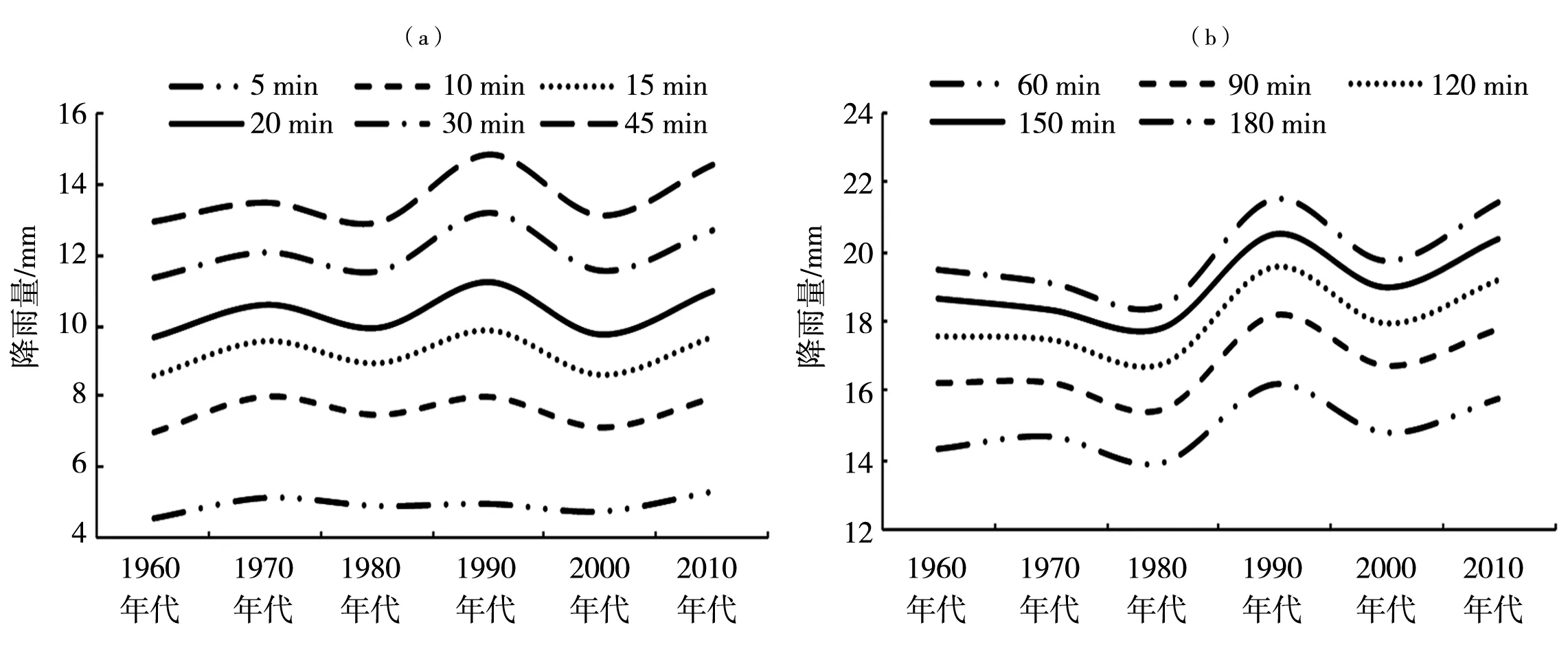
图1 吉林市5～45 min (a)与60～180 min (b)历时不同年代的平均暴雨雨量Fig.1 Average rainstorm amount with durations from 5 to 45 minutes (a) and from 60 to 180 minutes (b) in different decades in Jinlin City

3 暴雨强度公式推求

3.1 选样及频率分布曲线拟合方法优选

根据吉林城郊气象站1961—2017年的5～180 min共11个历时的降雨数据，对不同取样方法和概率密度函数的暴雨强度公式参数及误差进行比较(表2)，参数估计采用最小二乘法。吉林市为一般降雨强度地区，因此在精度检验时主要考虑平均绝对均方根误差。通过对比可知，年最大值法选样计算得到的暴雨强度公式平均相对均方根误差明显小于年多个样法。共有4种组合方式的误差满足要求，且在年最大值法取样时，P-Ⅲ型概率密度函数误差最小，平均绝对均方根误差和平均相对均方根误差分别为0.032 mm·min-1和4.28%。

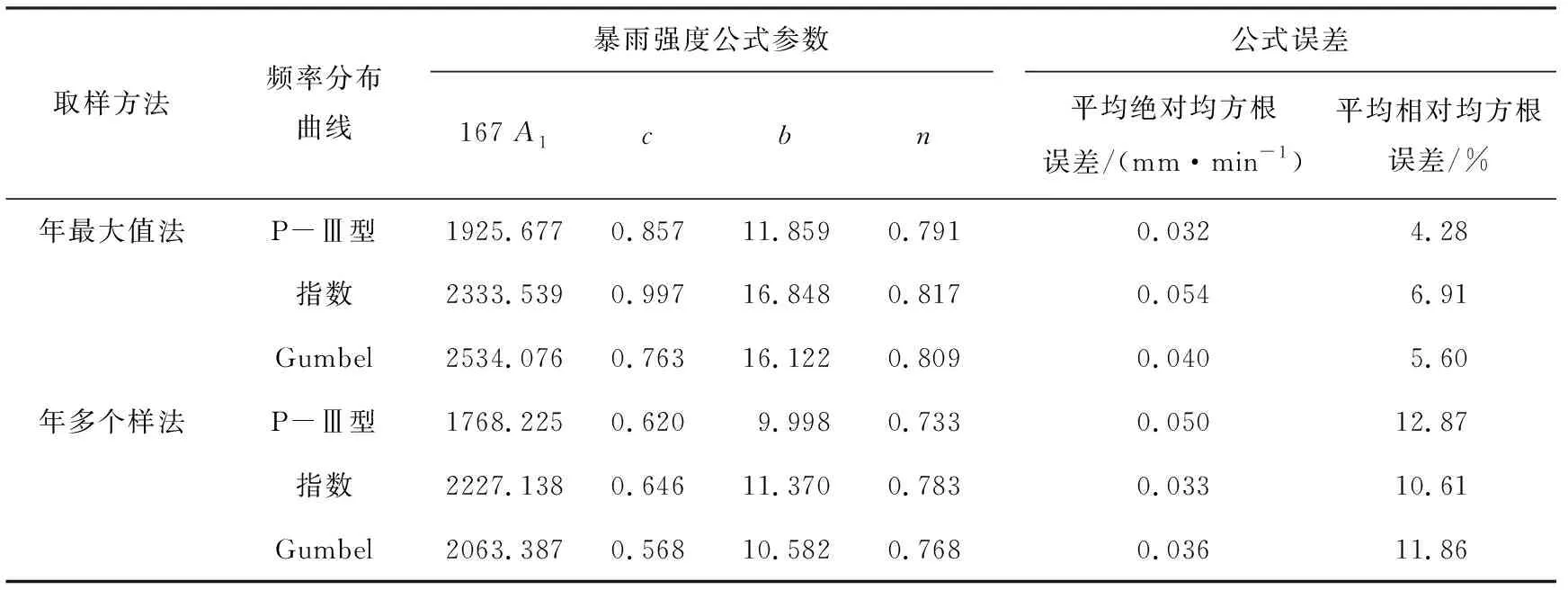
表2 不同取样方法和概率密度函数的暴雨强度公式参数及误差Tab.2 Formula parameters and errors of rainstorm intensity by using different sample selecting methods and probability density function

3.2 暴雨强度公式

采用年最大值法取样，P-Ⅲ型概率密度函数得到的吉林市新版暴雨强度公式精度最高，其公式如下：

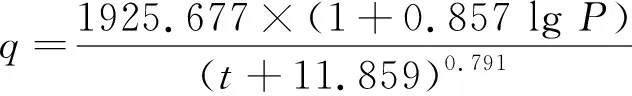
(11)

图2为吉林市5～180 min历时不同重现期的暴雨强度。

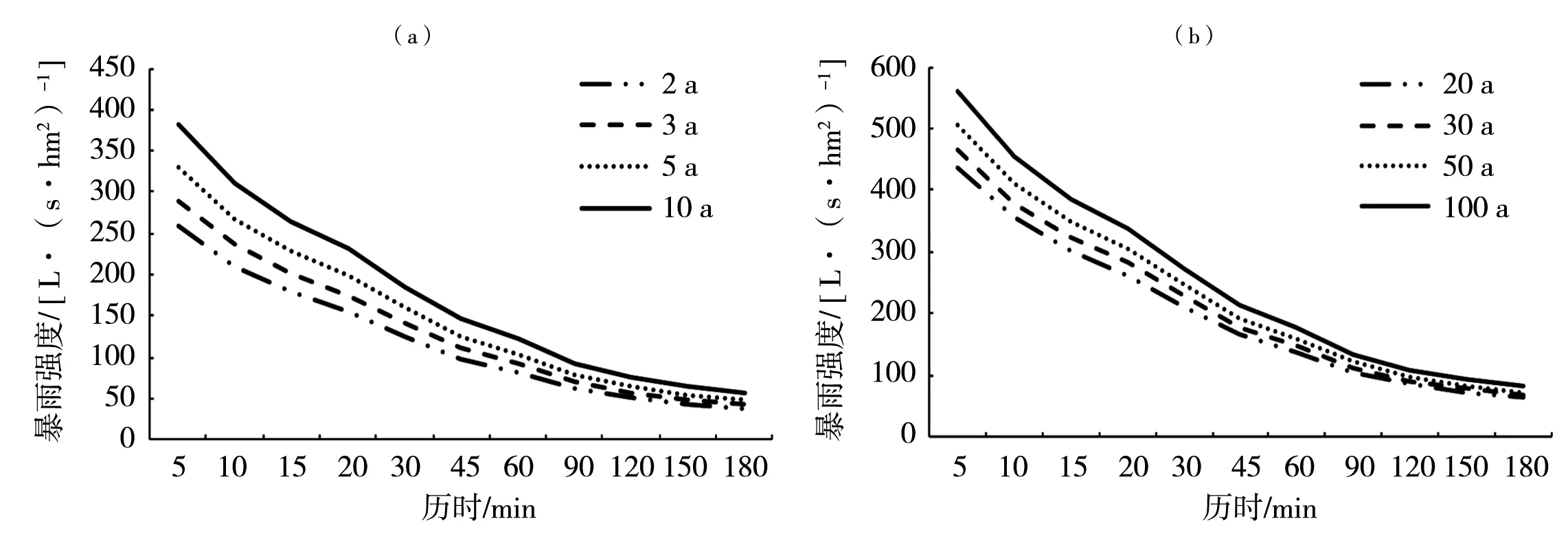
图2 吉林市各历时2～10 a (a)与20～100 a (b)重现期暴雨强度Fig.2 Rainstorm intensities of each duration under from 2 to 10 years (a) and from 20 to 100 years (b) return periods in Jilin City

3.3 新、旧版暴雨强度公式对比

吉林市旧版暴雨强度公式采用资料年限为1958—1983年，其公式如下：

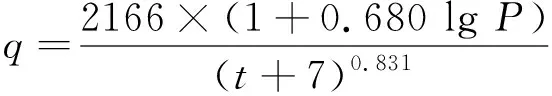
(12)

对旧版公式采用资料时段(A时段：1958—1983年)和新版公式采用资料时段(B时段：1961—2017年)的历史暴雨样本极值与均值进行比较(表3)。可以看出，B时段暴雨量极值在各历时下均大于A时段。B时段暴雨量平均值在5～20 min短历时下略小于A时段或与之相当；在30～180 min则大于A时段。

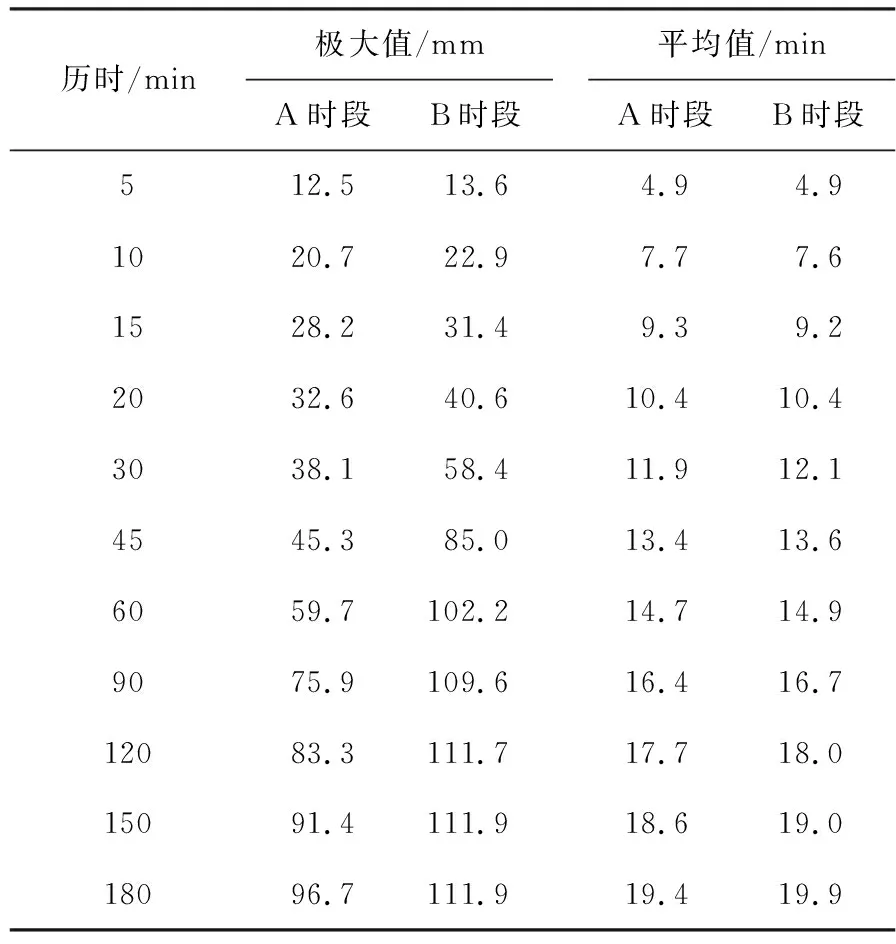
表3 吉林市两个时段暴雨样本极值与均值比较Tab.3 Comparison of rainstorm maximum and mean value in two periods in Jilin City

表4列出了吉林市不同历时和不同重现期暴雨强度变化率。可以看出，5～20 min历时新编公式计算的暴雨强度值与旧版公式相当或偏小，30～180 min历时新编公式计算的暴雨强度值偏大。在相同重现期水平下，随着降雨历时的延长，降雨强度的变化率逐渐加大。

表4 吉林市不同历时和不同重现期暴雨强度变化率Tab.4 Rainstorm intensity change rate with different durations and return periods in Jilin City 单位：%

4 芝加哥法短历时暴雨雨型推求

4.1 样本筛选及雨峰位置系数计算

表5列出吉林市30～180 min历时雨型参数。可以看出，各历时雨峰位置系数为0.36～0.58，计算各历时雨峰位置系数的加权平均值，得到综合雨峰位置系数为0.389。

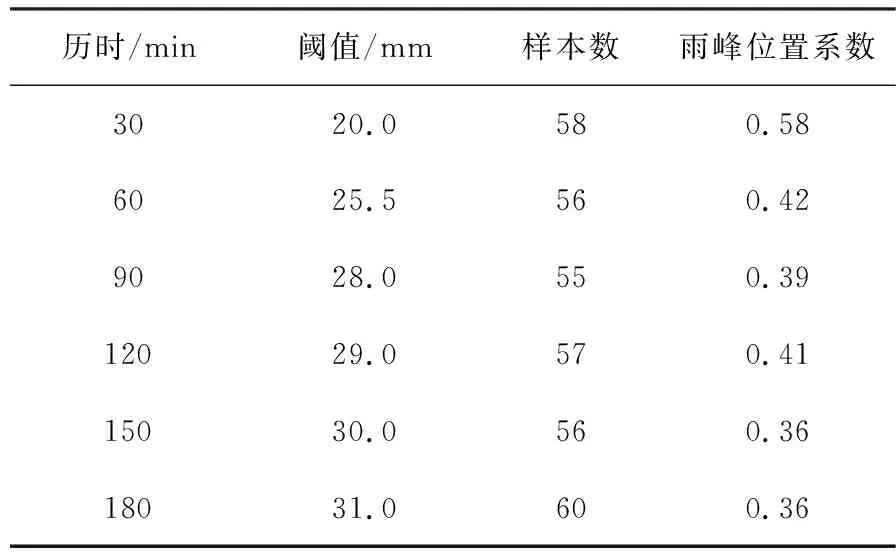
表5 吉林市30～180 min历时雨型参数Tab.5 Parameters of design rainstorm pattern in durations from 30 to 180 minutes in Jilin City

4.2 芝加哥法雨型推求

结合得到的新编暴雨强度公式及雨型参数，计算得到瞬时强度及各时段平均强度，最终建立起短历时暴雨雨型。在1980年以前，城市排水系统的重现期设计相对较低，一般在1 a以下，在城市快速发展的今天，已很难满足城市需求，因此国内城市排水系统的设计重现期已陆续提高到2 a以上[21]。以2 a重现期为例，分析吉林市的短历时雨型特征。图3为吉林市2 a重现期下各历时降雨瞬时强度。可以看出，30～180 min历时的雨型形态均大体呈单峰型，各历时瞬时雨强峰值为1.796～1.978 mm·min-1，无显著差异，90 min历时瞬时雨强峰值最大。各历时雨峰位置均偏前，雨峰出现时间分别在第12、24、35、47、59和70分钟，均位于偏整场降雨过程的1/2处之前，短历时强降雨较为集中，这与其他地区类似[27-28]。瞬时雨强峰值和雨峰位置均未随降雨历时的延长发生规律性变化。

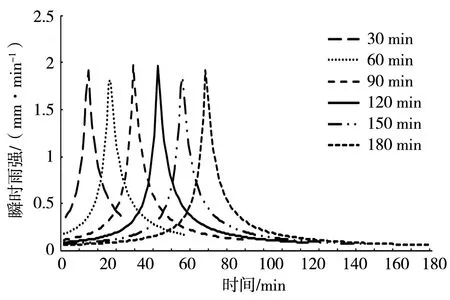
图3 吉林市2 a重现期下各历时降雨瞬时强度Fig.3 Instantaneous intensities of rainfall with different durations under 2 years return period in Jilin City

以5 min为一个时段，绘制吉林市60 min历时不同重现期累计雨量曲线(图4)。可以看出，各重现期累计雨量为29.56～63.78 mm。在降水开始的15 min以内，累计雨量的增长相对较为缓慢；20～30 min增长明显加快；30 min以后累计雨量的增长速度又明显放缓，累计雨量的变化特征与设计暴雨雨型形态一致。经计算可知，吉林市百年一遇的60 min历时暴雨过程累计雨量为63.78 mm。

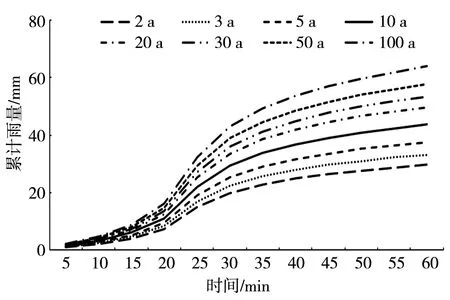
图4 吉林市60 min历时各重现期累计降雨量Fig.4 Accumulated rainfall values of different return periods under 60 minutes duration conditions in Jilin City

5 区域代表性分析

吉林市位于吉林省中部，地处长白山区向松嫩平原过渡地带，地理环境复杂，地势由东南向西北逐渐降低，暴雨等气象灾害时有发生[29]。图5为吉林市周边地区年平均暴雨日数空间分布。可以看出，近10 a来，吉林市周边地区的年平均暴雨(日降雨量≥50 mm)日数为1.4 d，空间分布上差异较大，由西南向东北逐渐减少，多则2.0 d或以上，少则低于1.0 d。由于短历时暴雨局地性较强，根据吉林市地形及邻近地区暴雨分布特征，吉林市城郊气象站的观测资料只能代表吉林市主城区，周边地区可参考使用。

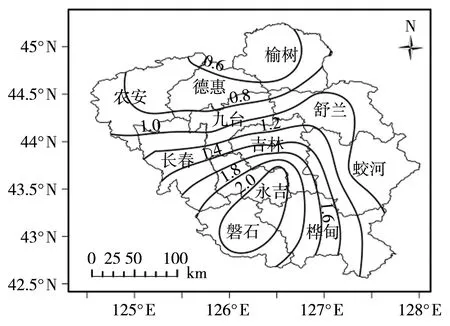
图5 吉林市周边地区年平均暴雨日数空间分布(单位：d)Fig.5 The spatial distribution of annual average rainstrom days in surrounding area of Jilin City (Unit: d)

6 结论与讨论

(1)采用年最大值法选样推算得到的吉林市暴雨强度公式较年多个样法推算的公式精度要高，能够满足相关要求。采用芝加哥法设计的雨型符合吉林市降水特征，短历时雨型形态呈单峰型，雨峰位置位于偏整场降雨过程的1/2处之前。

(2)新、旧暴雨公式差异较大，随着降雨历时延长雨强变化率由负转正，逐渐增大，分析原因主要为以下两点：一是吉林市短历时强降水的极值和均值均呈增大趋势，暴雨特性已发生改变，导致原有标准不再适用；二是受限于推求的技术手段和资料长度，旧公式的精度难以保证。

在气候变化背景下，城市快速发展对局地小气候的影响愈发显著，降雨强度在空间分布上极不均匀。由于受到资料限制，仅用城郊站单个站点代表整个城区，未能根据城市暴雨特征分区计算暴雨强度公式。在后续的研究中，可以考虑采用相邻相似地区数据或模拟预测数据[30]对降雨资料进行插补，或者对相邻地区暴雨强度公式进行必要修正[31]，以对资料不足的地区提供临时可用的暴雨强度公式，提高暴雨强度公式在空间尺度上的精确程度。在气候变化背景下，城市暴雨强度和频率持续变化，建议每隔10 a对吉林市暴雨强度公式重新计算。