基于平整度的改建公路用户油耗模型及其测算方法

刘 强，张志祥

(1.南京航空航天大学，江苏 南京 211106；2.江苏中路工程技术研究院有限公司，江苏 南京 211008)

0 引言

用户车辆油耗是公路运营期能耗的重要组成部分，降低用户车辆油耗是实现公路寿命周期节能减排的重要手段和措施[1-2]。已有的研究成果中，用户车辆油耗分析大都体现在公路的工可研究环节，主要用于评价公路项目对于用户出行的路网路径的改善。随着人民舒适便捷出行需求的不断提高，基于提升通行服务水平的公路改建或大修已逐渐成为公路管理部门的主要工作[3]，当前已有的研究成果大部分基于新建高速的用户效益评价，改建公路的用户社会效益评价尚无相关依据可循。

如何评估改建公路对用户油耗的影响是客观认识公路改建活动社会效益的重要途径。为实现用户节能效益的核算，本研究通过探讨路表平整度对汽车油耗影响机理，基于车辆油耗实测数据建立油耗模型，提出改建公路用户油耗效益核算方法，旨在为公路用户油耗及社会效益评价提供参考和依据。

1 平整度对车辆油耗的影响机理

从已有研究成果看，在路表特征参数中，平整度对车辆油耗影响最大[4-6]。由于路表构造波长的不同，路面可分为不同类型，其中对于波长大于0.5 m 的路段，可用不平整度(或平整度)来表征。平整度对于车轮驱动的影响大体可表征为不同路表波幅的影响，一般情况下，国际平整度指数IRI越大的路面其波幅越大[7-10]。简化的路表-车轮力学模型如图1所示。

图1 路表-车轮作用力学模型Fig.1 Mechanical model of wheel-pavement interaction

基于图1所示简化的力学模型，建立平整度与滚动摩阻力偶的计算方法，如式(1)所示。

Mf=FR·sinα·d·δ=FT·tanα·d·δ,

(1)

式中，Mf为滚动摩阻力偶矩；FT为车轮滚动牵引力；FR为滚动面法向作用力；α为滚动切面与路表面的夹角；δ为法向作用力FR重力方向分解力距原点距离；d为不平整度波幅。

从式(1)不难看出，假设δ一定，路面不平整度程度越高，相对应的波幅d越大，α角也越大。在FT一定的情况下，力偶矩Mf也越大，即车辆制动所需要克服力偶矩Mf所做的功也越大，车辆发动机油耗也越大。对于δ来说，一般路表不平整度状况不易用量化指标来衡量，但是从理论角度来说，波幅d越大，其力臂δ也越大。由此表明，不平整度程度越高的路面对汽车油耗的影响也越大。

2 基准状态平整度与油耗关系模型

在实测数据的基础上，定义模型基准状态，并给出基准状态下平整度与汽车油耗关系模型，并结合其他参数进行模型修正。

2.1 油耗参数采集

为了提高模型的精度，采用实测方法采集车辆油耗数据及路表特征参数[11-12]。油耗测试采用GPS发动机油耗检测系统，结合进油管单路测量法，对汽车发动机油耗量进行实时采集，并通过信号卡和GPS发送油耗数据和定位信息，通过无线传输模块发送到服务器后台进行处理和显示，测量精度达到3‰，如图2所示。基于相关规范采用标准测试方法采集路表参数[13-14]。

图2 油耗参数采集方案Fig.2 Fuel consumption parameter collection scheme

在测试过程中，对于测试的目标路段，在设定相应的行驶速度后，在到达既定位置后记录位置桩号及时间。在行驶过程中保证速度变化值不超过3%，同时尽量减少变道、超车等影响，并排除阴雨、大风天气测试工况。

2.2 测试样本路段

在全国范围内选择6个样本路段，共测试32 km，样本路段概况如表1所示。

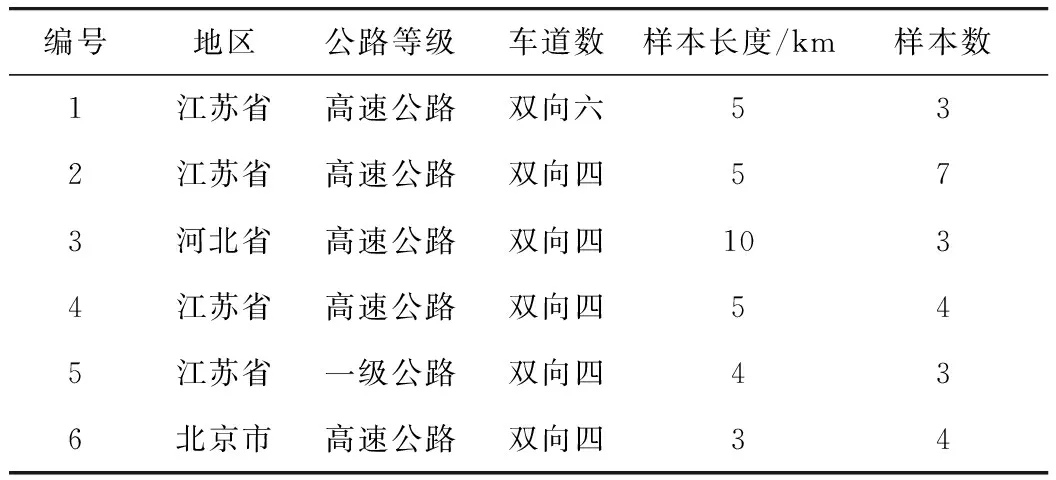
表1 样本路段概况Tab.1 Survey of sample sections

2.3 基准状况下油耗模型

(1)基准状态的定义

从改建公路的活动特征来看，其引起的参数变化主要是路面表层的相关性能，包括平整度、弯沉和摩擦系数SFC[15-18]，与外部气候环境等因素无关，因此为了探究平整度与油耗的关系模型，需要对外部因素进行统一定义，规避其变化给试验分析带来的影响。同时为了减少无谓的测试工作量，对弯沉、摩擦系数等变化参数按照样本情况，选择大概率数值区间进行定义，以充分降低其他参数对模型的影响。因此需要选择一个适宜的工况进行数据采集和分析。本研究将此工况定义为路面基准状态，结合样本路段路表特征数据分析，给出基准状态定义，如表2所示。

表2 基准状态定义Tab.2 Definition of reference state

(2)车型和车速标定

对于本研究来说，尽管不同车型的油耗值存在一定的偏差，但考虑到与相关研究成果的接轨和对比，因此按照相关课题研究情况，将车型分为5类，即小客车、大客车、小货车、中货车和大货车。

对试验路段埋设车辆预检系统，用以确定路段不同车型的平均行驶速度，并以此作为模型分析的基础[19]。对已安装实施的车辆预检系统设备的断面数据进行汇总分析，通过传感器记录行驶车速和车型轴型，计算不同车型的断面平均速度。根据限速水平，选择不同车辆的平均速度(见表3)，以此作为油耗测试的标定速度。

图3 车辆预检系统现场传感器安装Fig.3 Installing sensors of vehicle pre-test system

表3 基准状态不同车型车速标定Tab.3 Calibration for different vehicle speeds of reference state

(3)油耗模型样本数据

针对以上样本路段，按照基准速度分别进行不同车型的油耗测试，记录单元路段的车辆累积油耗，并根据里程核算平均油耗。样本路段平均油耗数据如表4所示。

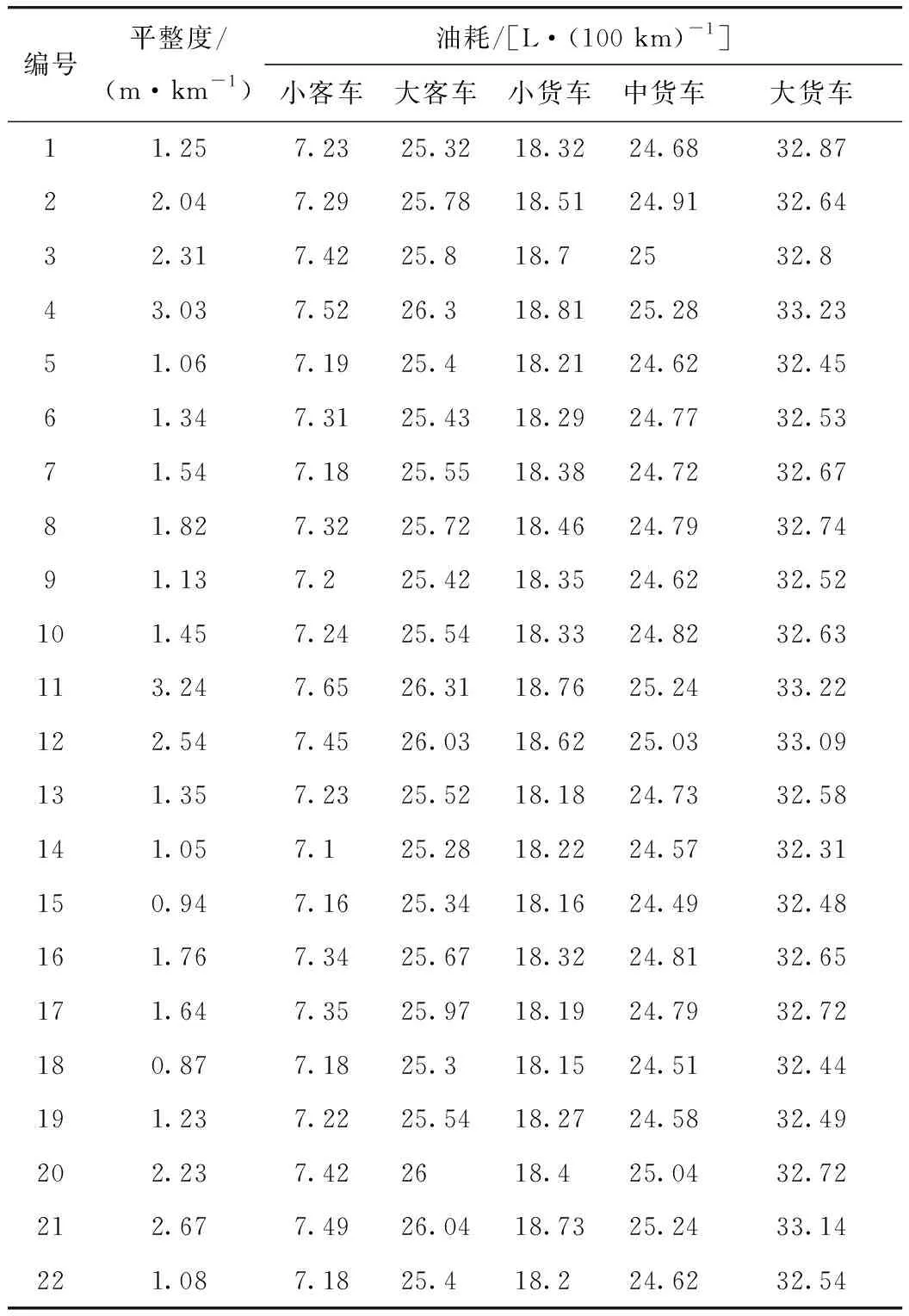
表4 油耗模型样本数据(部分)Tab.4 Sample data of fuel consumption model (partial)

(4)平整度与油耗关系模型建立

采用线性函数进行不同车型的油耗与平整度拟合，拟合相关系数均在0.8以上。在拟合过程中，对于极个别的模型采用指数等函数拟合可能具有更好的相关性，但是考虑到与同类型研究成果的比较及车型排量等因素，综合考虑仍采用一次线性函数进行拟合，油耗模型详见表5。

表5 基准状态平整度与油耗模型Tab.5 Reference state roughness and fuel consumption model

从表5可以看出，在其他约束条件限制值水平下，平整度与油耗存在较好的相关性，利用一次线型函数表达方式不难看出，随着平整度IRI的增加，油耗也呈现增大趋势。

3 油耗模型修正

3.1 修正方法

前文建立了基准状态下平整度与油耗的关系模型。考虑到路面的表观状况是随空间的不同而变化的，分别从路表参数弯沉和摩擦系数的角度对以上基准状态模型进行修正，以使模型适用于不同的路面工况。

从基准状态模型可知，5种车型的油耗Q与平整度相关模型均为一次线性函数，可用式(2)表示。从模型组成来看，其关键参数为A和B，也就是说对油耗模型的修正就是对A和B的修正。

Q=A×IRI+B。

(2)

根据参数之间独立性验证结果，用不同的弯沉值和摩擦系数对模型修正，以A′和B′表征弯沉和摩擦系数对于参数A和B的影响，以弯沉L为例，修正模型可表示为：

(3)

为了简化模型及计算过程可将以上函数表示为与原始参数A和B的乘积，即：

(4)

将修正弯沉f(L)对于参数A和B的影响函数可标记为k11和k12，修正摩擦系数f(S)对于A和B的影响函数分别标记为k21和k22，则综合以上因素对于A和B的影响可用K1和K2来进行表示：

(5)

归根结底，对于基准状态模型的修正也就是需要建立弯沉与摩擦系数对于A和B的影响。

3.2 基于弯沉和摩擦系数的模型修正

在基准状态模型基础上，分别针对不同车型计算A和B，并将其与基准状态模型的A和B进行比较，并建立k11和k12与弯沉L，k21和k22与摩擦系数SFC之间的相关关系，计算结果如表6～表7所示。

3.3 基于速度参数的油耗模型修正

前面的模型是建立在标定车速的基础之上的，考虑到实际改建公路由于车流量、车道数、限速等条件的制约，不同车型的车速必然存在差异。为了提高模型对不同工况的适应性，本研究重点考虑速度参数，对模型进行进一步修正。

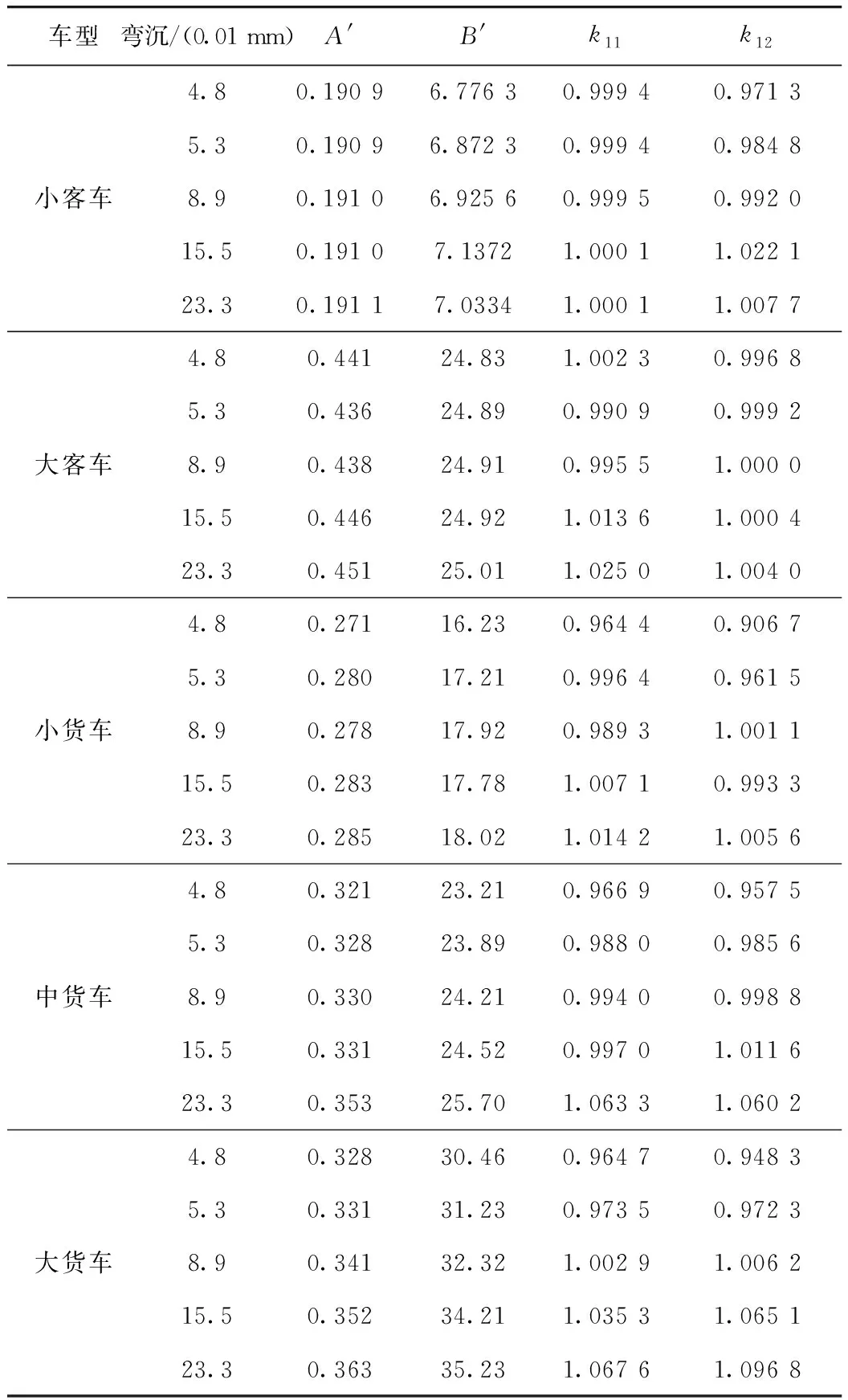
表6 弯沉修正参数Tab.6 Deflection correction parameters

对于模型修正仅考虑速度参数，由于相关研究模型均在基准状态下建立，其对应的速度参数V对于不同车型来说也有相应的界定，在修正过程中重点针对修正系数来进行分析。为了便于计算，采用油耗修正系数m与速度比λ作为计算指标，在实测数据的基础上，分析速度V与车辆油耗Q之间的相关关系，以小客车为例，分析油耗与速度之间的关系以及m与λ之间的关系，如图3～图4所示。根据分析结果，可得出适用于任意改建公路工况的用户油耗计算模型，如表8所示。

4 用户节能效益核算方法

4.1 核算方法及流程

如前文所述，基于本研究对象改建公路。由于改建活动给公路平整度等表观参数带来提升，势必会给公路用户带来相应的节能效益，因此核算过程中可基于本研究的计算模型分别计算改建前后公路用户的油耗差，以此来表征用户效益。计算公式为：

表7 摩擦系数修正参数Tab.7 Correction parameters of friction coefficient

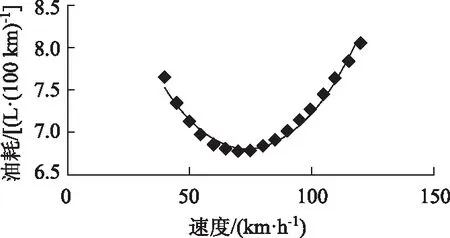
图4 小客车油耗与速度拟合曲线Fig.4 Fitting curve of fuel consumption vs. speed of car

图5 小客车油耗修正系数与速度比的相关关系Fig.5 Correlation between fuel consumption correction factor and speed ratio of car

表8 修正后平整度-油耗模型Tab.8 Corrected model of roughness vs. fuel consumption

W=∑Wk，

(6)

Wk=(∑ΔQqi×ρq×δq×Si+∑ΔQcj×ρc×

δc×Sj)×365，

(7)

ΔQqi=Q″qi-Q′qi，

(8)

ΔQci=Q″ci-Q′ci，

(9)

式中，W为用户节能效益；Wk为单元k路段年节能效益；ΔQqi和ΔQci分别为汽、柴油车单车节油效益；ρq和ρc分别为汽、柴油密度；δq和δc分别为汽、柴油折标油系数；Si和Sj分别为汽、柴油车行驶里程；Q″qi和Q″ci分别为改建后汽、柴油车单车油耗；Q′qi和Q′ci分别为改建前汽、柴油车单车油耗。

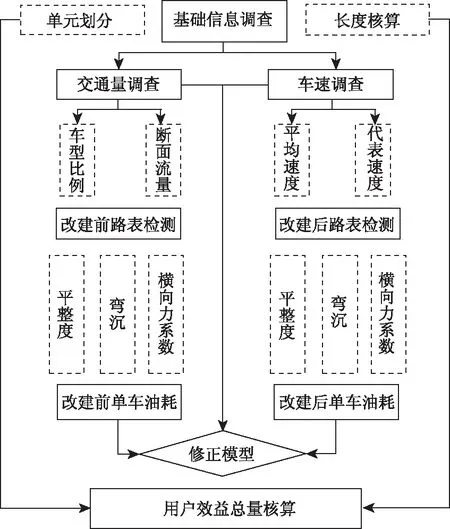
图6 用户节能效益核算流程Fig.6 Flowchart of user energy saving benefit accounting

4.2 案例应用

根据本研究成果，针对宁宣高速公路改建工程对研究成果进行了工程应用，根据表8中的计算公式采集改建前后相关数据，计算用户年节能量结果，如表9所示。

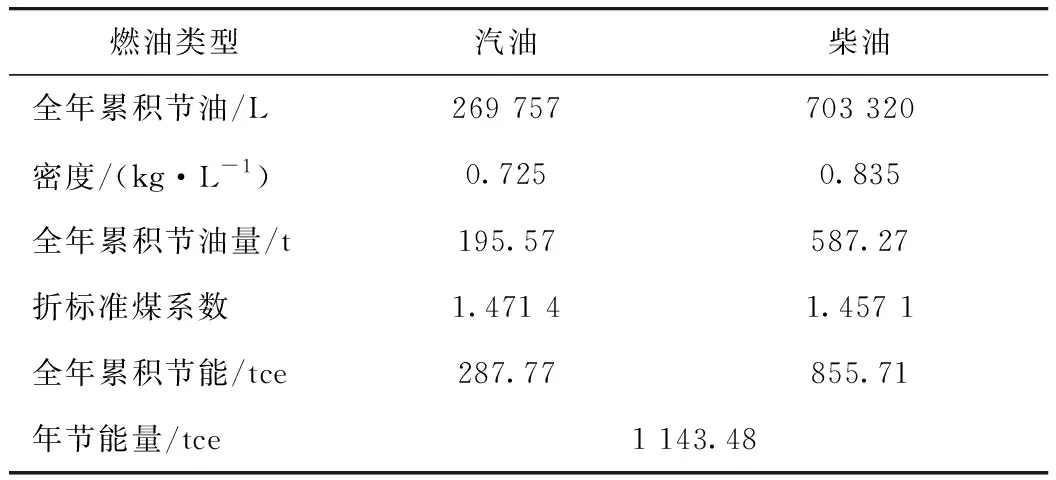
表9 宁宣高速改建工程用户节能效益计算Tab.9 Calculation of energy saving benefits fir users of Nanjing-Xuancheng expressway reconstruction project

从工程应用情况来看，本研究提出的用户油耗效益核算模型和节能效益核算方法合理地评估了实施改建给用户带来的节油、节能效益。应用结果表明，改善路面平整度对于提升路面行驶舒适性、提高用户出行效益具有重要意义。

5 结论

本研究基于改建公路平整度研究探讨了用户油耗模型核算方法，得到以下结论：

(1)表征路面平整度的宏观构造波长引起的车辆滚动摩阻力矩是影响车辆油耗程度的主要因素，平整度指数IRI越大，车辆油耗越大。

(2)制定了车辆油耗和路表参数测试与采集方案，并根据实测数据，建立了基准状态下车辆油耗与平整度的单参数模型。

(3)针对弯沉、摩擦系数和车速，建立了平整度与车辆油耗的修正模型，提出了改建公路用户节能效益核算方法和流程，并进行了案例分析。对改建公路的用户节能效益评价具有重要的参考借鉴作用。