星轮式电动爬楼轮椅的结构设计与稳定性分析
王 涛,申 燚,陈一鸣,文俊伟,袁明新
(江苏科技大学机电与动力工程学院,江苏 张家港 215600)
随着我国经济的不断发展,高层建筑数量快速增加,老人以及残疾患者爬楼愈发不便。我国目前已进入老龄化社会,截至2017年底,中国60岁及以上老年人口已超过2.41亿,到2050年预计将达到4.87亿[1]。因此,爬楼轮椅成为助老助残热点产品之一。王占礼等[2]通过单轮毂电机驱动三星轮组进行爬楼翻转,爬楼机构结构紧凑,动作灵活,但动力有所欠缺,且对翻转过程中的平衡性考虑较少;李育文等[3]设计了履带式爬楼轮椅,虽稳定性及其对各种路况的适应能力有所提高,但也加剧了楼梯的磨损;Quaglia等[4]将三星轮与履带相结合,实现自动爬楼,但履带造成楼梯磨损的不足仍存在;周秋雨等[5]通过在驱动轮上安装杆件翻转实现轮椅爬楼,但杆件前端橡胶套与台阶接触面积小,受力集中,易损坏。针对已有设计的不足,本文设计了基于三星轮翻转机构的爬楼轮椅,轮椅可分平地和爬楼两种工况进行结构自适应调整,前后两组星轮翻转机构以及座椅调平机构可保证轮椅的动力和稳定性。
1 爬楼轮椅总体设计
1.1 爬楼轮椅总体设计
爬楼轮椅结构如图1(a)所示,包括星轮翻转机构、底座升降机构、座椅调平机构和普通轮等。
当在平地运动时,底座升降机构降低,靠4个普通轮支撑;爬楼时,底座升降机构升起,星轮翻转机构着地,调平机构同时调整以保证人体水平。星轮翻转机构如图1(b)所示,星轮架中心装有齿式离合器[6],当离合器吸合时,轮架与中心齿轮轴联接成整体,电机驱动三星轮组旋转,轮椅实现爬楼功能;当离合器分离,中心齿轮轴传动,分布在中心齿轮周边的齿轮带动3个星轮转动,实现三星轮平地驱动。
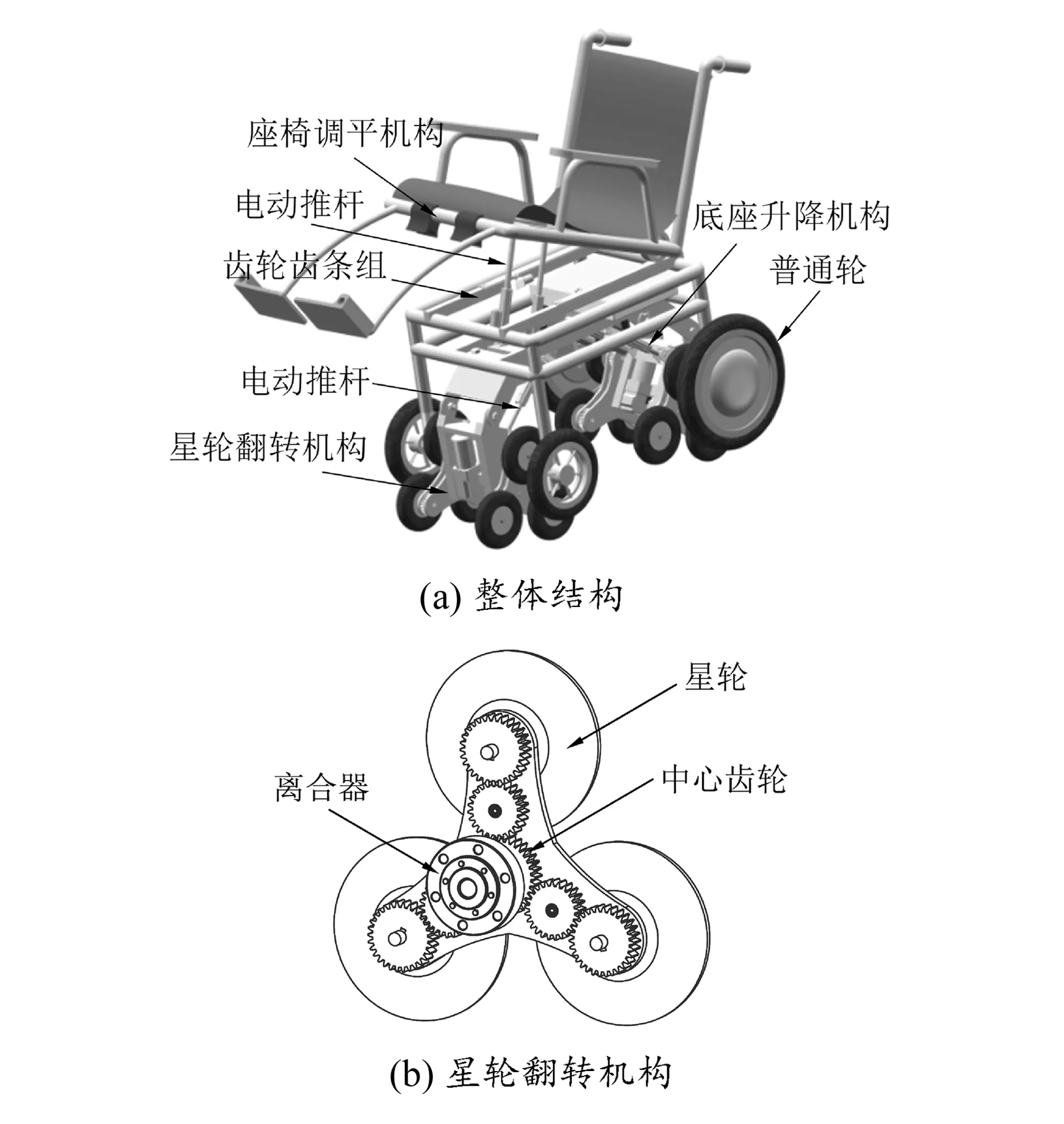
图1 爬楼轮椅三维模型
本文的设计完全区别于市面上已有的基于定星轮翻转机构的轮椅,通过星轮机构的收放,实现了爬楼和平地行驶两种工况的切换,提高了轮椅的运动效率。
1.2 爬楼轮椅结构设计
1.2.1星轮翻转机构设计
根据我国《建筑楼梯模数协调标准》的规定,台阶高应为140~210 mm,踏步宽应为220~320 mm,楼梯角度不宜大于38°。文中取踏步宽a=300 mm,台阶高b=150 mm。定义余量e为处于较高位置且接触台阶的星轮轴与台阶边缘间的距离,为了保证楼梯攀爬的质量,规定余量e最小为30 mm。图2展示了三星轮组向上翻转爬升一个台阶的过程,虚线轮廓为三星轮组的运动轨迹。
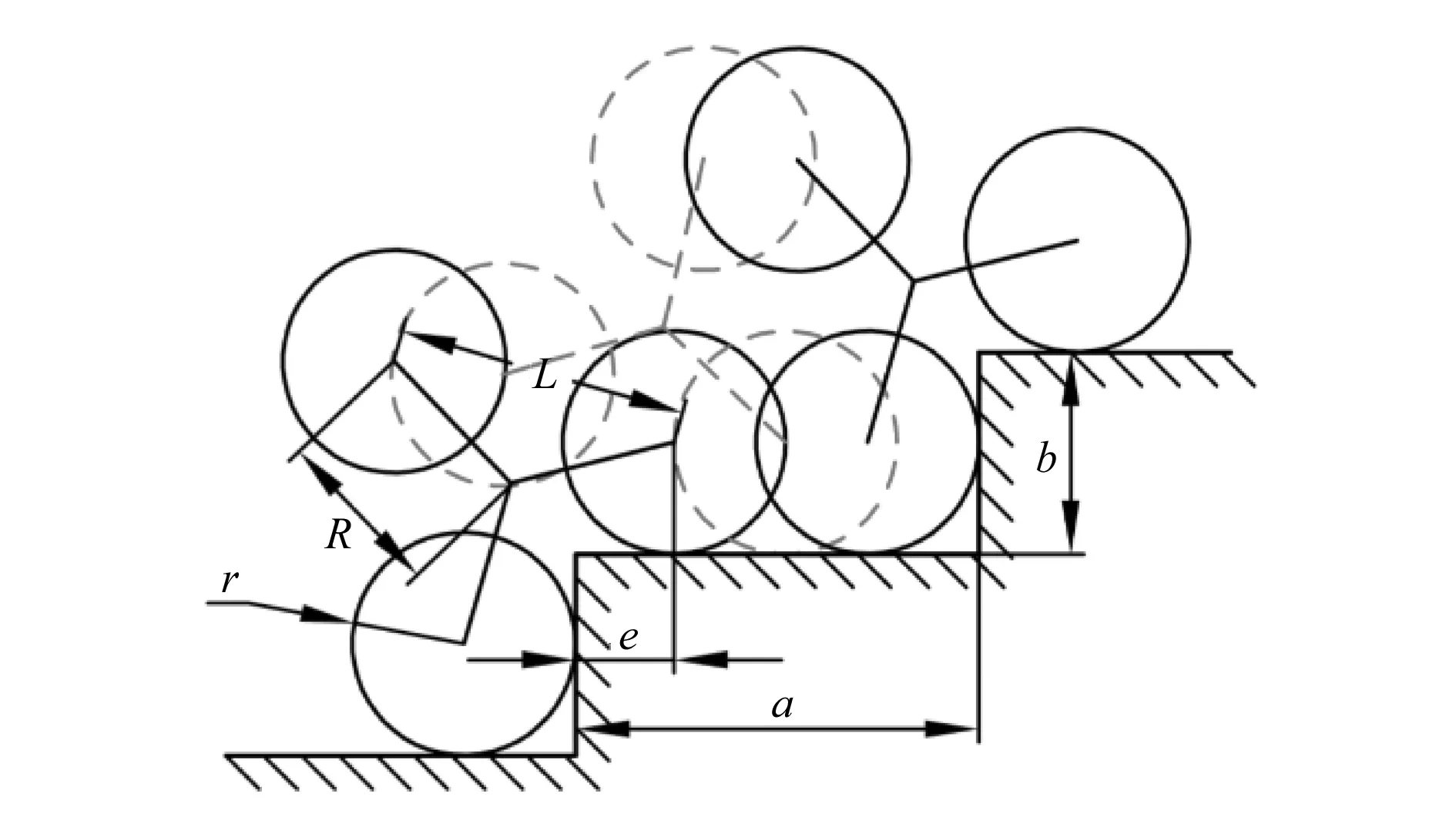
图2 星轮翻转示意图
由图中几何关系可得:
(1)
L2=b2+(e+r)2
(2)
式中:L为星轮轴距;R为三星轮架半径;r为星轮半径。在完成一个台阶攀爬时,星轮滚动距离为2πr/3,与r,e之和需大于台阶踏步最大尺寸,约束条件如下:
L≥2r
(3)
(4)
由式(1)~(4)得R≤153.7 mm,47.7 mm≤r≤93.2 mm,因此本文设计的三星轮架半径R=115 mm,星轮半径r=87 mm,符合要求。
1.2.2其他机构设计
底座升降机构由电动推杆和三星轮架组成,如图3所示,且机构对称安装在椅架前后。
由图可以看出,电动推杆动作,三星轮架绕推杆端部铰接点旋转,三星轮架位置高度得以调节,轮椅实现平面移动和楼梯移动方式的切换。
座椅调平机构如图1(a)所示,主要由电动推杆和安装在导轨上的齿轮齿条组组成。通过推杆动作,座椅以后端为支点旋转改变仰角,同时齿轮齿条组在步进电机驱动下带动座椅平动,从而保持座椅水平。

图3 底座升降机构简图
1.3 轮椅星轮驱动系统设计
1.3.1星轮驱动电机功率计算
轮椅工作在不同工况下对电机功率和转矩的要求不同,本文主要以平地行驶、爬坡、爬楼3种常见工况对电机功率及转矩进行计算。文中轮椅质量不超过50 kg,载质量不超过85 kg,取轮胎滚动摩擦系数δ=0.05。根据国家对电动轮椅的规定[7],设计轮椅最大平地行驶速度为10 km/h,最大爬坡速度为2 km/h,最大爬行坡度为12°。规定三星轮翻转速度为4 r/min,即轮椅每分钟攀爬12级台阶。
轮椅在地面正常行驶时,普通轮着地且由后轮轮毂电机驱动,地面对轮胎静摩擦力Ft为驱动力。不考虑空气阻力,驱动力Ft与行驶阻力存在如下关系:
Ft=Ff+Fs+Fa
(5)
即
(6)
式中:Ff为后轮滚动阻力;Fs为坡度阻力;Fa为行驶加速阻力;Te为轮毂电机转矩;Ra为后轮半径;m为整体质量;φ为爬行坡度;k为质量旋转换算系数;at为行驶加速度;g为重力加速度。
行驶加速阻力在轮椅速度达到最大值v时仍然存在,故轮椅平地行驶所需最大功率P为:
(7)
式中:Ra=200 mm;m=135 kg;k=1。
由式(6)、(7)可得:轮椅平地行驶时,φ=0°,v=2.7 m/s,at=0.3 m/s2,故轮毂电机在平地行驶时的功率P1=111 W,转矩Te1=8.2 N·m;轮椅爬坡时,φ=12°,v= 0.5 m/s,at=0.1 m/s2,故轮毂电机爬坡时的功率P2=148 W,转矩Te2=59 N·m。根据上述计算可得,后轮轮毂电机最小功率为74 W,最小转矩为30 N·m。
轮椅爬楼主要基于星轮翻转,考虑到轮椅重心上下波动会导致电机转矩不断变化[8],为方便计算,对电机最大输出转矩Tmax进行估算。取力臂最大值为三星轮架半径R,最大作用力为mg,则星轮电机的最大瞬时功率P3为:
(8)
式中:R=115 mm;三星轮转速n=4 r/min。由此得到P3=165 W,Tmax=156 N·m,则单个电机最小输出扭矩为78 N·m。
1.3.2驱动电机选型
由上文可知,单后轮轮毂电机最小功率为74 W,在此选择常见的16寸单边轮毂电机即可满足要求。
星轮驱动电机选择转矩T为12 N·m的86步进电机,并配以040蜗轮蜗杆减速器以及MA860H-DSP型驱动器。考虑机械传递效率η,电机减速前的最小转速n0可根据电机最大输出转矩进行求解:
(9)
式中:η=0.8;T=12 N·m。故n0=66 r/min。
由n0确定减速器减速比为20,从而设定爬楼时步进电机的转速为80 r/min。
2 轮椅爬楼过程的力学分析
轮椅爬楼功能的设计是整体设计中的重点,现从力学方面研究轮椅爬楼的条件。为了方便求解,假设在爬楼过程中,轮椅和使用者的整体重心相对运动系统不产生位置变化。
在轮椅爬楼过程中,三星轮翻转,单个星轮与台阶接触容易出现打滑的情况,研究此状态下轮椅不打滑的力学条件是实现轮椅爬楼功能的重点。在此忽略轮胎的滚动摩擦力。轮椅受力示意图如图4所示。
由图4中力和力矩平衡条件可得:
N1+N2=G
(10)
F1+F2=f1+f2
(11)
T1+T2-N1Rcosβ-N2(l+Rcosβ)+Gd=0
(12)
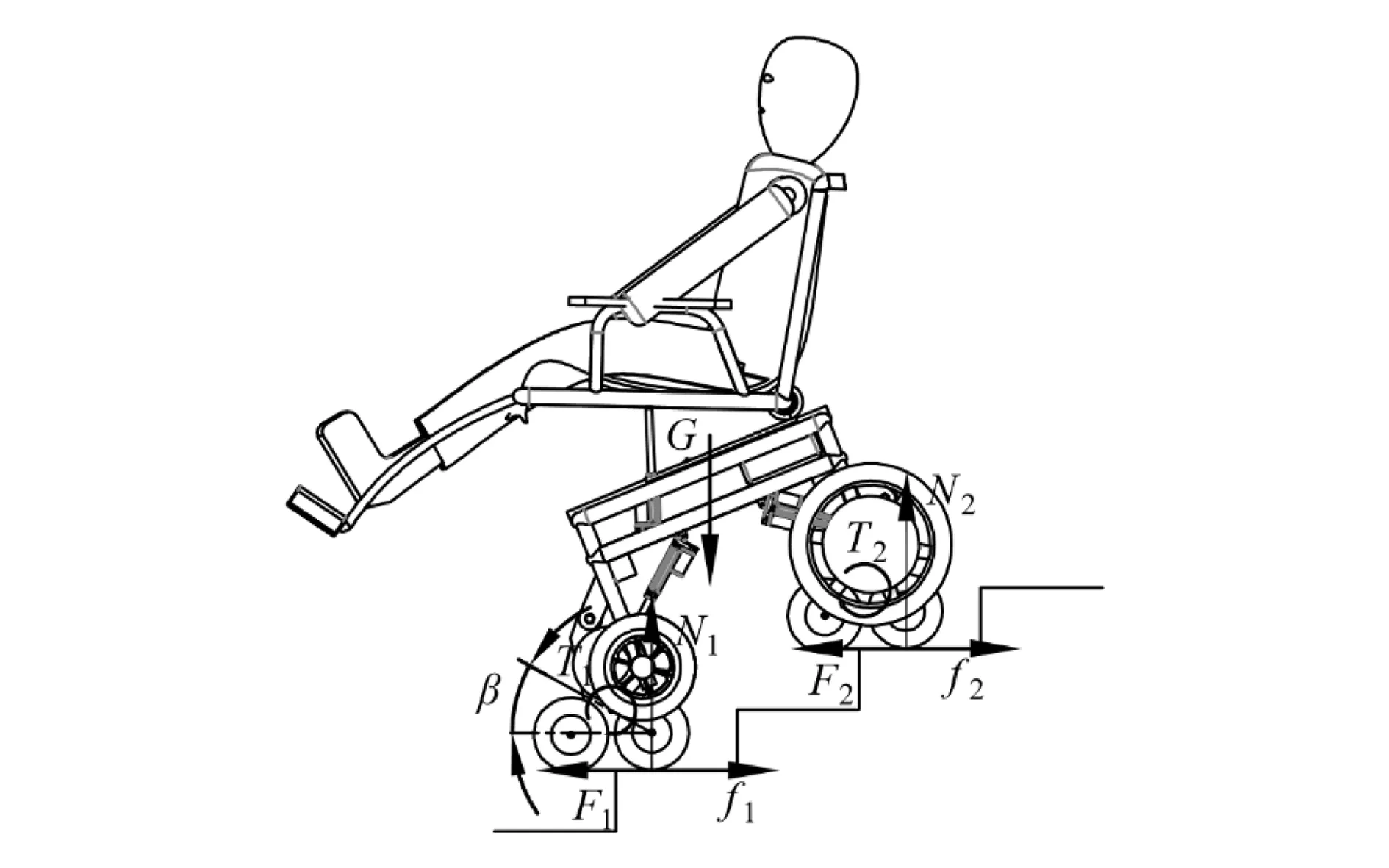
图4 轮椅受力示意图
式中:N1为台阶对前部三星轮组的支撑力;N2为台阶对后部三星轮组的支撑力;G为轮椅与使用者的整体重心;F1与F2分别为前、后电机转矩提供的力;f1与f2分别为前、后轮胎所受静摩擦力;T1与T2为前、后驱动电机输出转矩;l为三星轮中心轴间的水平距离;d为重心与前三星轮中心轴间水平距离;β为星轮轴和三星轮中心轴的连线与台阶面之间的展角。
为了防止轮胎打滑,驱动力应小于最大静摩擦力,即
F1<μN1
(13)
F2<μN2
(14)
式中:μ为轮胎与台阶面滑动摩擦系数,取值0.7。
将根据已有参数所求出的T1与T2作为参考,验证所选驱动电机,经验证符合要求。
3 轮椅爬楼稳定性分析
本文设计的轮椅其日常工作主要有爬楼和平地行驶,在工作中会存在打滑、爬楼动力不足和倾翻等异常工况。其中,轮椅的倾翻不仅与其结构设计的合理性直接相关,还是严重涉及人身安全、最可能发生的异常工况,因此着重对轮椅倾翻进行研究。轮椅在下楼过程中较上楼更易发生倾翻,故本文以轮椅下楼过程的倾翻临界条件来判断其稳定性[9]。
3.1 轮椅倾翻模型建立
在下楼过程中,假设轮椅在某一时刻由于自身惯性发生了质心对前星轮与台阶面接触点的转动,轮椅开始倾斜,如图5所示。
以图中星轮与台阶面接触点为原点建立直角坐标系,系统质心的坐标为(xc,yc)。轮椅倾斜过程中存在倾翻临界位置,即质心在X轴的投影为0处。当轮椅不恢复正常状态,继续倾斜,系统质心超过临界位置,轮椅将倾翻。
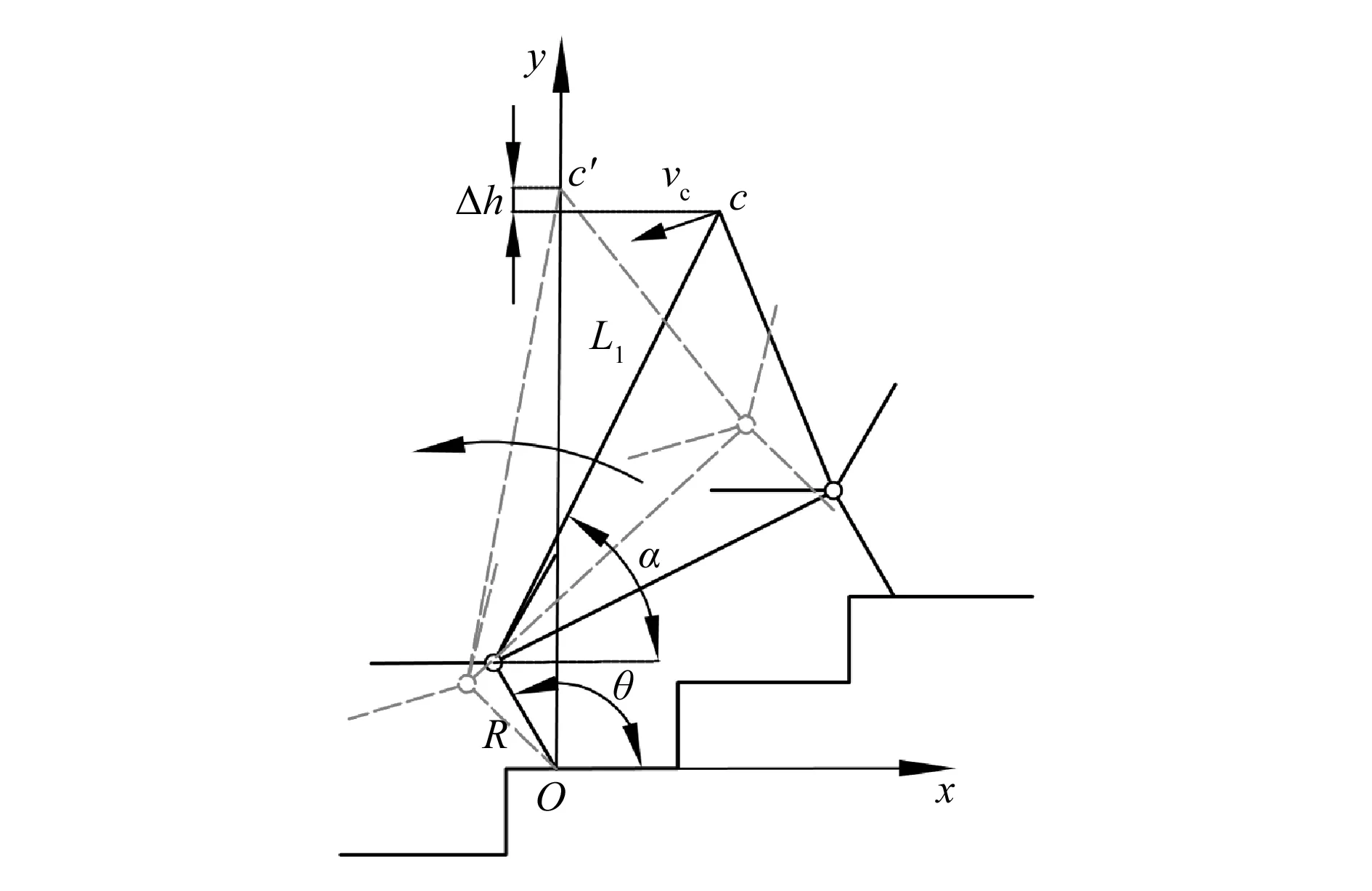
图5 轮椅倾翻示意图
从能量角度考虑,轮椅从正常位置到倾翻临界位置所需能量为轮椅的势能增量ΔEp,此时轮椅由惯性产生的能量为Ek。轮椅不发生倾翻,表明Ek无法满足轮椅到达倾翻临界位置的能量需求,即Ek<ΔEp。在此定义阻翻能量ΔQ作为轮椅是否会倾翻的判断标准:
ΔQ=ΔEp-Ek
(15)
当ΔQ≥0时,轮椅可能会发生倾斜,但不会倾翻,即使发生倾斜,最终也会处于稳定状态;当ΔQ<0时,轮椅可能会倾翻,且ΔQ的值越小,倾翻的可能性越大。
由图5可得:
(16)
(17)
xc=L1cosα+Rcosθ
(18)
yc=L1sinα+Rsinθ
(19)
(20)
式中:vc为质心瞬时速度;t为图2所示初始状态下三星轮转过角度θ所用的时间;α与轮椅结构尺寸和楼梯角度有关,在爬楼过程中为固定值68°;L1为质心位置到前部三星轮组中心轴的距离,其值为0.82 m;初始状态下,三星轮架与台阶间的夹角为θ0,其值为75°。
3.2 轮椅倾翻能量分析
现求解阻翻能量与不同变量间的关系曲线。三星轮转速n分别取为3 r/min、6 r/min、16 r/min、32 r/min、48 r/min,对式(16)~(20)进行整合后与各参数值代入式(15),利用MATLAB求解不同转速条件下阻翻能量随时间的变化规律,结果如图6所示。

图6 阻翻能量曲线
图中曲线末端横坐标为轮椅下降一个台阶的完成时间,阻翻能量最小值发生在下降一个台阶的动作将要完成时,此时轮椅的稳定性最差。转速越大,阻翻能量最小值越趋近于0,轮椅倾翻可能性越大。
现将三星轮转速n限定在3~60 r/min范围内,结合实际情况以及为了求解方便,首先求得不同整数转速n下的阻翻能量曲线;然后取得每条阻翻能量曲线上最小的阻翻能量值,记为ΔQmin,当ΔQmin<0时,轮椅会倾翻;最后分别以n和ΔQmin为横坐标与纵坐标进行曲线拟合,进而求解得到如图7所示的最小阻翻能量曲线。
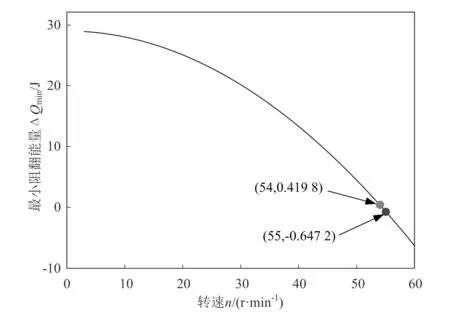
图7 最小阻翻能量曲线
由图7可知,当n=54 r/min时,ΔQmin=0.419 8 J;当n=55 r/min时,ΔQmin=-0.647 2 J,故当三星轮转速n≤54 r/min时,轮椅不会倾翻,当n>55 r/min时,轮椅倾翻。
由此可知,本文设计的轮椅三星轮转速n=3 r/min,远小于轮椅倾翻的临界转速,因此可确定该轮椅的稳定性达到要求,确保了轮椅爬楼的安全性。
4 结束语
为了解决老人及残疾患者爬楼困难的问题,本文提出了一种新型电动爬楼轮椅的设计方案,通过三星轮组四驱实现其爬楼功能,与其他爬楼轮椅相比,其驱动性能和稳定性较为突出。通过对轮椅爬楼状态的分析可知,三星轮的转速对爬楼轮椅的稳定性影响很大,三星轮转速越低,轮椅爬楼稳定性越好。
本文所设计的轮椅虽然能满足正常使用要求,但仍存在诸多不足,比如轮椅采用了四轮驱动来增加驱动力,但也增加了轮椅质量和成本,又如在研究中并未对座椅进行设计,对使用者乘坐舒适性有一定影响。因此在后续研究中,需要对轮椅进行驱动方案的优化,按照人机工程学对座椅进行设计,从而提高轮椅的综合性能。

