铣削加工中的刀具振动主动控制仿真研究

赵文举，龚 俊，刘 洋

(兰州理工大学机电工程学院，甘肃 兰州 730050)

机械加工过程普遍存在振动现象。振动会影响被加工件的表面质量，加剧刀具的磨损，剧烈的振动会使切削加工不能继续进行，从而降低生产率，对机床和夹具不利。在动态的铣削加工过程中，再生型颤振是影响铣削加工精度的重要因素。由于铣削是不连续的切削加工过程，其产生的周期性动态切削力会导致刀具与工件之间发生振动，在一定条件下，便会发生颤振。目前，主要有主动和被动两种铣削颤振控制方法。被动控制方法主要通过改变切削参数来扩大稳定性区域，但这样并不能真正地提高加工效率[1]；主动控制方法通过实时改变系统阻尼或刚度来减小系统的振动，又或者设计主动控制器来控制作动器的输出，直接抵消刀具或工件的位移，从而达到控制目的。随着作动器和控制理论的发展，颤振主动控制研究已然成为颤振控制的主要研究方向。江浩等[2]设计了用于减小铣削振动的主动减振平台，通过控制干扰信号的频率达到抑制铣削振动的目的，取得了良好的效果，但要预先知道干扰信号的频率，有一定的局限性。Denkena等[3]为了抑制加工系统的振动，将电磁作动器和机床主轴结合在一起，增大加工系统的阻尼，该主动控制方法结合铣削加工颤振系统和作动器产生的力来建立闭环动力学模型，并采用数值分析方法验证了所提方法的有效性。郑平旭等[4]针对刀具和工件的相对振动，提出了一种基于H∞的铣削加工主动控制方法，抑制了铣削振动。乔晓利等[5]将主动磁轴承力学模型和铣削加工颤振动力学模型相结合，在建立的铣削加工闭环控制系统动力学模型的基础上，采用目前成熟的PID控制方法，达到了控制振动的目的。刘晓丽[6]基于压电驱动器，采用模糊神经网络算法主动控制立铣刀的振动。本文在立式铣削动力学模型的基础上，提出一种针对立式铣削加工中刀具振动的控制方法，并对该方法的控制效果进行了MATLAB/Simulink环境下的时域数值仿真验证。

1 铣削动力学模型

1.1 动态铣削力建模

参考杨毅青等[7]的铣削力建模方法以及窦炜等[8]的铣削力计算方法，计算考虑再生效应的动态铣削力，图1 所示为立式铣刀动态铣削力计算模型。

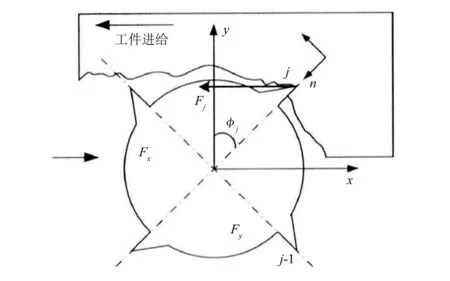
图1 立式铣刀动态铣削力计算模型

由于铣刀铣削时不止一个切削刃参与切削，因此特定的刀齿动态切削厚度h(φj)为

h(φj)=(ftsinφj+nj-1-nj)·δ(φj)

(1)

式中：φj为铣刀的切削角度；ft为刀具每齿进给量；nj为当前刀齿法向振动位移；nj-1为前一刀齿法向h(φj)振动位移；δ(φj)为开关函数，用来判断刀齿是否在切入角φs与切出角φe之间。δ(φj)的表达式为：

(2)

将X和Y方向的振动位移x，y向振动位移方向的法向n投影：

n=-xsinφj-ycosφj

(3)

则动态切削厚度h(φj)可以表示为：

h(φj)=(Δxsinφj+Δycosφj)δ(φj)

(4)

式中：Δx，Δy为X和Y方向的瞬时切削厚度。

将切削力的切向分量Ft,j和法向分量Fn,j向固定坐标系X和Y方向投影可得：

(5)

式中：Ft,j=Ktaph(φj)，其中ap为轴向切削深度，Kt为切向切削力系数；Fn,j=KrFt,j，其中Kr为径向切削力系数；Fx,j为X方向的切削分力；Fy,j为Y方向的切削分力。

对投影在X和Y方向的所有刀齿上的瞬态铣削力代数求和，得到铣刀在X和Y方向上总的动态铣削力为：

(6)

式中：Fx和Fy分别为铣刀在X方向及Y方向上动态铣削力。

整理得到动态铣削力：

(7)

其中：

cos(2φj)]}

Knsin(2φj)]

式中：A为时变的动态力方向系数；Δ为动态切削厚度；Kn为法向切削力系数。

1.2 铣削系统的Simulink动力学仿真

在铣削加工过程中，刀具-工件系统发生振动使得动态切削厚度发生变化，导致铣削力随之发生改变，动态的铣削力变化又会作用于铣削系统，使之产生相应的振动，构成了闭环铣削加工动力学系统，铣削系统动力学仿真框图如图2所示。刀具与工件之间的振动产生动态铣削力Fx，Fy，动态铣削力Fx，Fy为输入量，经过传递函数Gx(s)和Gy(s)得到输出的位移信号x(t)和y(t)；同时，铣削过程是多齿不连续切削的过程，当前齿的位移滞后于前一刀齿的位移，从而产生位移差Δx和Δy,使得静态切厚h随之变化。

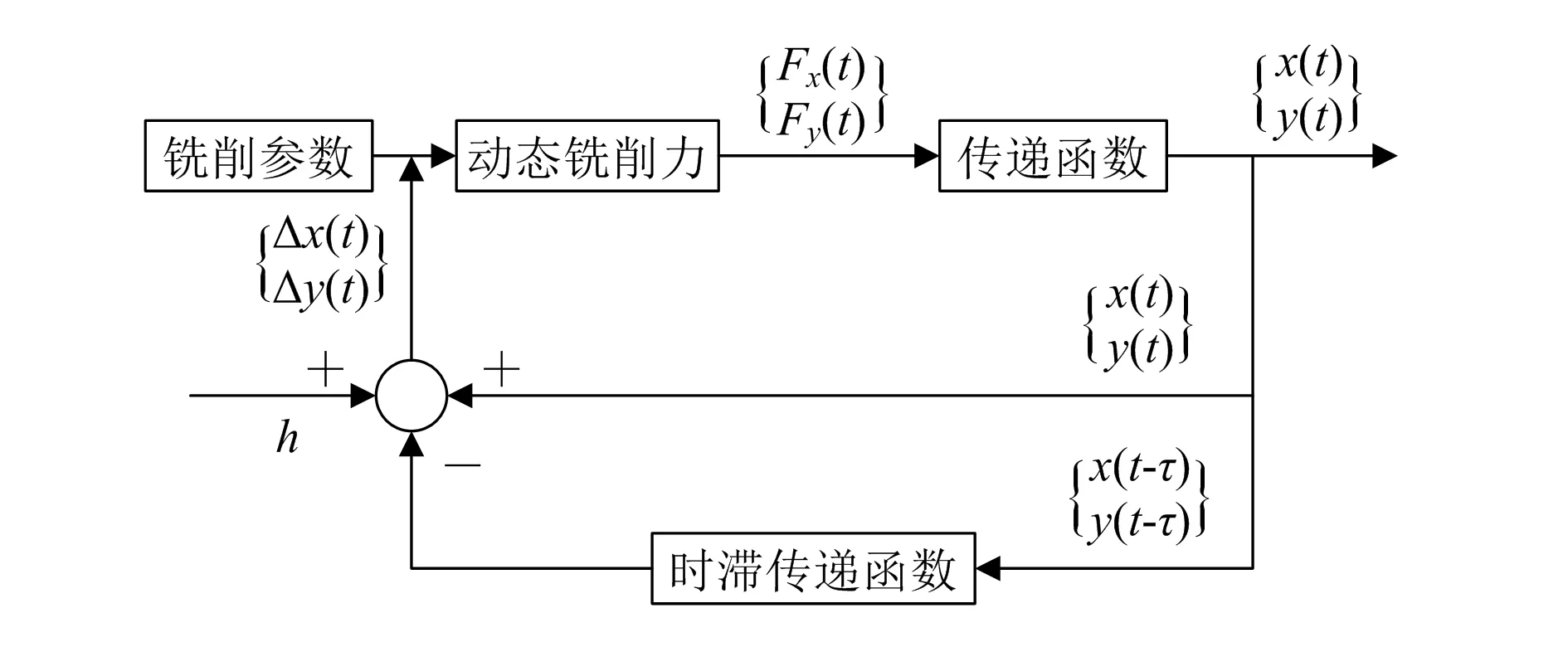
图2 铣削系统动力学仿真框图

2 控制器的设计

由于建模误差、模型参数的变化以及外部扰动会导致铣削系统的不确定性，因此本文采用一种基于H∞的鲁棒混合灵敏度方法[4]来控制铣削时刀具的振动。基于H∞的控制方法，其实就是设计镇定控制器函数F(s)的过程，使得闭环系统稳定且回路传递函数的H∞范数最小。用基于H∞的控制方法设计控制系统时,由于系统本身的误差、外部扰动都会造成系统的不确定性,因此控制器的设计过程其实就是求解一个闭环控制器的过程。

本文以X方向的传递函数Gx(s)为例，设计基于H∞鲁棒混合灵敏度方法的控制器来控制X方向的振动位移，设计流程图如图3所示。

图3 控制器设计流程图

其中，根据铣削颤振理论,铣削系统可简化为X和Y方向两个互相垂直方向上的二自由度振动系统,其动力学方程为：

(8)

式中：mx和my分别为X和Y方向的等效质量；cx和cy分别为X和Y方向的阻尼系数；kx和ky分别为X和Y方向的刚度系数。

对控制器X方向的铣削系统的动力学方程进行拉氏变换就可以得到传递函数Gx(s)：

(9)

式中：ωnx为X方向的固有频率；ζx为X方向的阻尼比。

将铣削系统的铣削参数代入式(9)得到X方向的传递函数Gx(s)如式(10)所示：

(10)

如图4所示，基于H∞的鲁棒混合灵敏度方法的核心是选择合适的加权函数W1，W2，W3，再利用构造好的增广对象模型与加权函数设计控制器。其中，r(t)为外部参考输入，u(t)为控制输入，y(t)为观测输出，e(t)为系统误差，F(s)为控制器传递函数，y1a，y1b，y1c为评价输出。

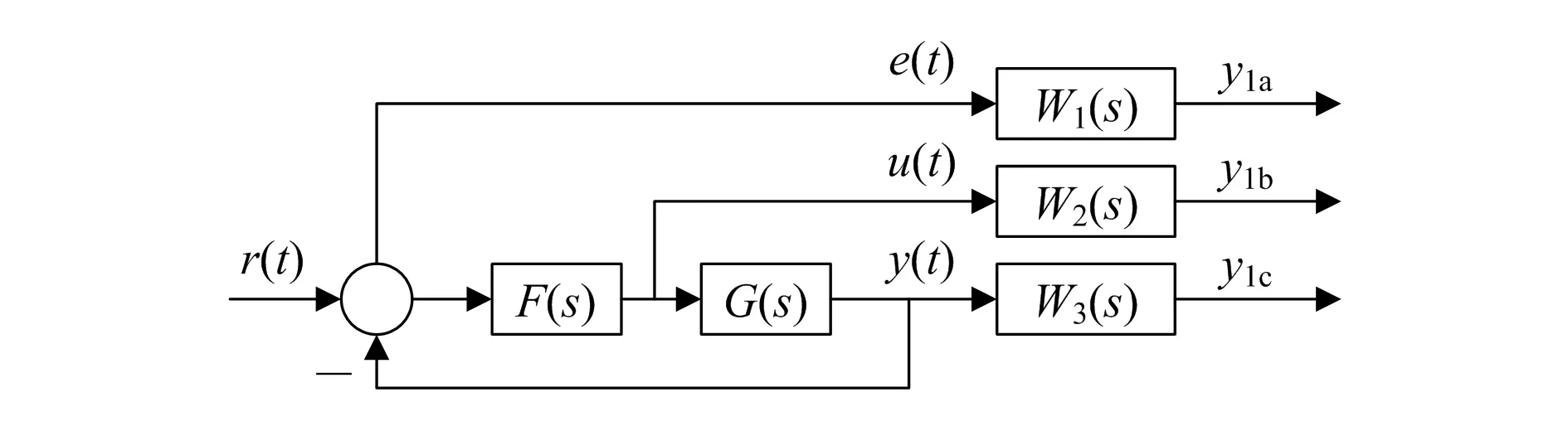
图4 加权函数问题的控制结构框图

综上所述，根据加权函数问题的控制结构框图的结构，选择形式为对角真实有理函数阵[9]的加权函数W1，用来降低系统误差e(t)。为了限制控制信号的大小，选择形如W2的加权函数；为了增强系统的高频抗干扰能力，选择高通滤波器形式[4]的加权函数W3。加权函数W1，W2，W3的表达式如式(11)所示:

(11)

F(s)的具体求解过程[10]为，通过MATLAB鲁棒控制工具箱中的augtf函数结合加权函数W1，W2，W3构造增广函数矩阵，在此基础上，利用hinfsyn函数求解出控制器F(s)。控制器F(s)的表达式如式(12)所示:

F(s)=-[5.248 5×108(s+1 200)(s2+225.4s+3.169×107)(s2+225s+3.2×107)]/[(s+1 000)(s+4 042)(s2+231.3s+3.193×107)·(s2+4.681×104s+6.43×108)]

(12)

3 仿真分析

为验证控制器的控制效果，本文选择直径为19 mm的3齿立铣刀，铣削方式为逆铣，切削参数为每齿进给量0.022 mm、轴向切深2 mm，铣削系统稳定切削时，根据表1所示的铣削仿真参数，在MATLAB/Simulnk环境下搭建基于H∞鲁棒混合灵敏度方法的仿真模型，系统的仿真框图及子系统如图5，6所示。对基于H∞的控制方法进行时域仿真，得到输入铣削系统的铣削力，如图7所示，X，Y方向振动位移的控制效果仿真图如图8，9所示,表明在动态铣削力激励下，有、无控制作用时刀具的振动位移变化。

图5 控制系统仿真框图

图6 控制系统子系统仿真控制

表1 铣削仿真参数

图7 输入系统的铣削力信号

图8 X方向的振动位移信号

根据图8和图9的仿真结果可以看出，在未加控制的情况下，X方向稳定铣削时的最大振幅大约为34.6 μm，在基于H∞的鲁棒控制器F(s)的作用下，X方向稳定铣削时的最大振幅大约为24.5 μm，X方向振动位移信号的振幅约降低了29.1%；在未加控制的情况下，Y方向稳定铣削时的最大振幅大约为59.5 μm，在基于H∞的鲁棒控制器的作用下，Y方向稳定铣削时的最大振幅大约为33.6 μm，Y方向振动位移信号的振幅约降低了43.5%。仿真结果说明，基于H∞鲁棒混合灵敏度的控制方法可以有效抑制铣削加工系统X方向和Y方向的振动位移，提高立式铣削的质量。

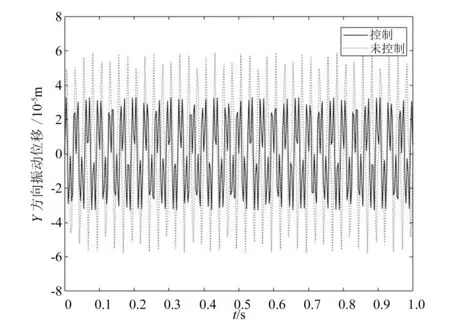
图9 Y方向的振动位移信号

4 结束语

本文基于H∞的鲁棒混合灵敏度方法对刀具振动的主动控制具有良好的控制效果,为控制铣削加工过程中的刀具振动提供了一种新的控制方法；同时，也为提高立式铣削的质量以及抑制铣削加工系统X方向和Y方向的振动位移给出了立式铣削闭环控制系统主动控制器的设计方法。但该方法还有一定的局限性，需要相关试验验证控制方法的控制效果，以便进一步优化控制器参数。