喻理于例、手到心到:“应用信息论”导论课的设计
黄生祥 邓联文 廖聪维 罗衡 李旭光


[摘 要] 通过多年研究生新生课程“应用信息论”的教学实践,教学团队总结凝炼了一套引导学生们克服畏难心理、快速理解信息量、信息熵等基本概念的方法。在“应用信息论”的导论课堂,通过一个天平称重的益智游戏导入信息量概念,运用头脑风暴法讨论信息量及信息熵的数学形式,多视角解读最大熵定理,达到喻理(信息论)于例的目的。通过实际动手计算及证明,更好地帮助大部分研究生新生手到心到,建立起足够的学习和研究的信心,取得了很好的教学效果。
[关键词] 信息论;课程设计;益智游戏;脑力风暴
[中图分类号] G642.0 [文献标识码] A [文章编号] 1674-9324(2021)04-0128-04 [收稿日期] 2020-04-22
一、引言
信息论是电子通信领域的重要基础课,无论对于高年级本科生还是研究生,学习起来均有较高的难度[1,2]。近年来,教学团队一直坚持面向本院电子通信工程、电子科学与技术等专业的研究生新生开设“应用信息论”课程,其目的是普及信息论知识和思维方法,以期在今后的科研中将信息论作为思考问题及解决问题的工具。
信息论课程具有概念抽象、公式繁多的特点[3,4],初学者感到畏难。部分研究生虽然在本科四年级时选修了相关的课程,例如“信息论与编码”,但是普遍反映听不懂、考试后基本忘记了所学知识。
二、一个富有信息量的益智游戏
大部分的信息论课程,开头都将对香农的有趣研究经历做一些介绍。一般介绍完香农对信息论的贡献之后,就开始讨论概率或者信息量。但是我们认为进入正题前,利用一个经典的益智游戏来激发学生的好奇心很有必要。因此,我们选择了一个富有信息量的益智游戏,让学生们互动起来。
问题的提出:天平称球问题。已知12个球中有一个重量不标准的次品球,如何用一个无砝码天平称最少的次数,将这12个球中的次品球确定下来。
首先安排1~2名学生在黑板上书写解题思路,同时也让其他学生拿出笔和纸亲自琢磨解法。从这几年情况来看,所有的学生都能推测得到称3次能确定出次品球,学生都能够对个别情况做出合理的判断,分析出部分解决方案,但是很少有学生能够全部给出解答。
在较充分地讨论之后,我们对这个问题开展了信息量的分析。天平称3次(3种状态:左边重,右边重,平衡),最多的结构有3=27种。但是异常球可能是12个球中的一个,可能轻也可能重,所以现实状态只有24种。从原理上,一定能3次称完。
现在,考虑这12个球,其中一个是或轻或重的次品的各种可能性。如果这个球是“轻”的次品,记为-,“重”的次品,记为+,因此,可能的次品分布情况是1+、1-、2+、2-……12+、12-。得益于这些符号的表示,我们可以较方便地把3次称球的全部过程都描述清楚。
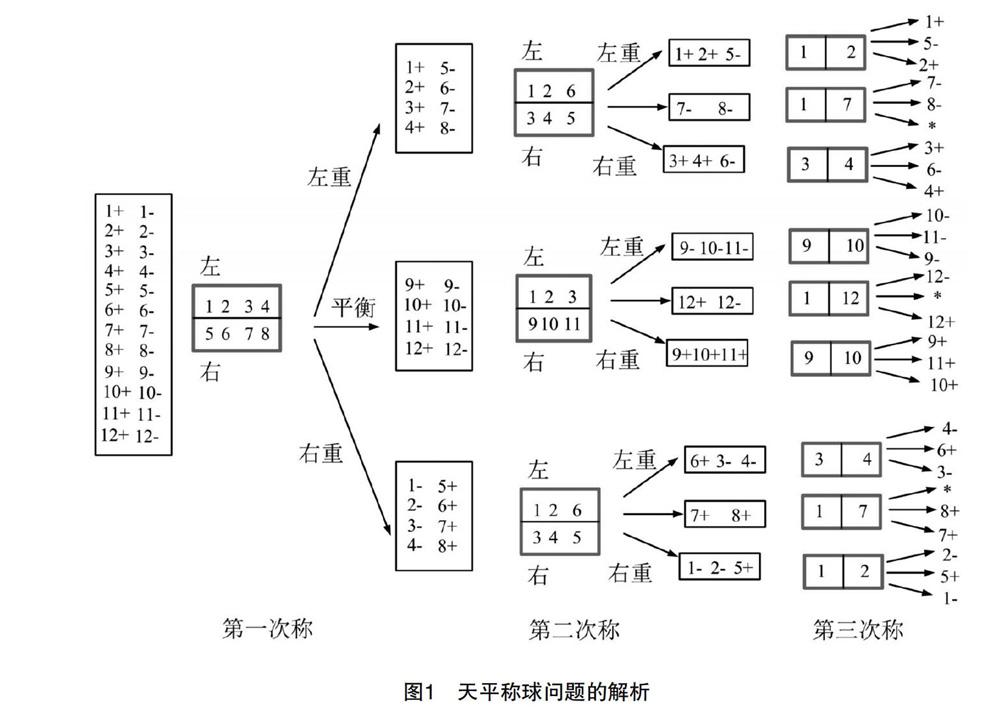
图1示意了天平称球问题各种情况的完整解析。这里仅举一种情况作为说明。先拿出1~4号球置于天平之左,5~8号球置于天平之右,做第一次称重操作。若左侧天平较重,则可能的情况包括:1~4号球中有一个较重,或者5~8号球中有一个较轻。在新一次的称重中,应该合理地交换,增加新的信息量。于是左侧天平保留1号、2号球,换上6号球;右侧天平则保留5号球,换上3号和4号球。若仍然是左侧为重,则说明所换的3号、4号、6号球为标准球,仍然是1号球或者2号球较重,或者5号球较轻造成的。于是第三次的称重则衡量1号球和2号球即可,较重的那一个即非标准球,或者二者的平衡即可以导出5号球较轻的结论。其他的情况,可对照图1做类似的解读。
这个小游戏说明,如果一个随机实验在所有结果上的概率分布为均匀分布时,可以保证它可提供的信息量最大。本实例的展示,至少可以起到以下几个作用:①拉近课程与学生们的距离,让听者可以开动脑筋,进入思考状态。②本算例蕴含着信息论的一些基本的思想,图1所示的解析,实质上是通过实验设计,将24种可能性充分均匀地散布到三次称重之后,与后面要引入的信息熵概念形成了呼应关系。
三、一次关于“信息熵应该是什么数学形式”的头脑风暴
头脑风暴的过程在信息量及信息熵的导入过程中起到关键作用。一般来说,依概率对信源进行建模是必须的一道教学流程。由于建模的过程非常重要,建议把这段话写到黑板上,而不能仅仅通过PPT展示。
对M元离散信源,即x1、x2、…xM,根据这些信源出现的概率,建立了相应的“概率场”模型来描述,即这里的约束条件是;
然后,我们引入一个讨论过程:如何度量这些信源事件的信息量。为了表述清楚“消息所表达的事件越不可能发生,信息量就越大”这个意思,可以举出不少例子来。例如,“那一天发生了8级大地震”,这句话蕴含的信息量就很大,因为8级大地震是一个小概率的事件。因此,要给出一个表达式I(x)来衡量信息量的话,它一定是一个关于概率p的单调减函数,即概率越大,信息量的函数值越小。另一方面,根据生活常识,若干独立事件的信息量要可以叠加。如果对于系列独立事件的信息量收集得越充分,对这些事情方方面面的把握就越清楚。
然后我们开始引导大家来讨论,如下表达式是否可以作为信息量的函数。
四、三种最大熵定理的证明方法
虽然通过信息量的讨论引入了信息熵定义,也举了几个例子,让大家计算了不同的信息熵,例如某种天气概率的信息熵、等概率掷硬币的信息熵、等概率掷骰子的信息熵等。但是,多年來的教学实践表明,最大熵定理的证明过程,对于更好地理解信息熵帮助很大。
这里首先说明,什么是最大熵定理。信源中包含n个不同离散消息时,信源熵H(X)有必然满足如下关系:
这种证明方法有几个优势:①强化了对信息熵函数的上凸性质的认识。②证明过程之所以能够成立,在于log函数的加强吸收和自变量能够分子、分母抵消,这有利于加深大家对信息熵函数形式的记忆。
第二种证明方法是利用相对熵的概念。对于x事件的概率分布p(xi)及y事件的概率分布q(yi),相对熵被定义为:
五、重视互动、当堂计算
参加课程的学生,能够通过数学运算的过程,形成相互竞技、观摩的一种氛围,可以形成较活泼生动的课程讨论。在本课程教学过程中,大量开展了当堂计算、手动证明、画图示意,PPT演示同时起到串接和提醒的作用。本教学团队成员均达成共识,即PPT里的数学式子是静止的;只有通过粉笔写到黑板,才成为一个讨论和研究的课题;只有通过师生的讨论和解析,并且经过有限步骤的推演、证明,才成为鲜活的观念,植入到学生们的头脑中。
在导论课上,我们简单地介绍了香农编码。只有通过让一位學生在黑板上演算、其他同学在教室当堂演算这样的发掘过程,才暴露出大家存在的问题:①从小到大,没有进行过十进制小数转化二进制小数的运算,不能理解为什么是乘2取整;②机械地背诵了大于1整数转化而二进制数的除法过程,不能明确判断余数出现顺序和二进制数顺序的对应关系;③不能理解二进制小数中,多位循环的情况。
我们设计了这样的简单的课堂互动:让大家分别将十进制的11、0.5、0.7转化为二进制数。然而结果让人大跌眼镜,完全无提示的情况下,在2分钟内能够完全正确实现这三个数字二进制转化的学生的比例不超过20%。教师演示出多项式展开、标注出二进制数每一位的权重对应关系,70%以上的学生才恍然大悟,能够计算得出正确结果。这反映出我们的基础数学教学环节,学生们的实际演算能力、对数字的敏感性仍然不够高。而对数字、数学式子的不敏感,也正是信息论教学环节的最主要障碍。
以上这些情况,通过信息论的课堂教学,均不同程度地有所缓解。从课程考试结果来看,全部参与课程的学生,都能够很好地完成信息熵的较准确值的计算。
六、结论
“应用信息论”是电子通信专业研究生新生的重要基础课。本课程教学团队通过多年来的课程实践,总结出导论课如何开展案例教学的新方法。利用天平称重的益智游戏、头脑风暴法讨论信息量及信息熵的数学形式、多种方法证明最大熵定理,从不同角度引导上课的研究生新生克服畏难心理,较快速理解信息量、信息熵等基本概念。
参考文献
[1]沈连丰,叶芝慧.信息论与编码[M].北京:科学出版社,2004.
[2]朱雪龙.应用信息论基础[M].北京:清华大学出版社,2001.
[3]钟义信.信息科学原理[M].北京:邮电大学出版社,1996.
[4]傅祖云.信息论——基础理论与应用[M].北京:电子工业出版社,2007.

