一种新型燃烧器壁温监测传感器数值分析
张 勇,黄 森,赵 蕾
(国家能源费县发电有限公司,山东 临沂 273400)
0 引言
火电机组作为电网主力电源,关系到电力安全生产及电网的稳定。大容量火电机组技术进步和自动化程度的提高对电力工业的发展和国家资源的合理利用都有着极其重要的意义。随着现代高速计算机和高效计算方法的出现,建立电站锅炉生产过程模型[1]并进行数值模拟计算变得可行。模拟得到的丰富信息,能为锅炉高效生产和稳定运行起到重要的指导作用[2-3]。
现代电站对锅炉受热面、燃烧器壁面温度监测方法主要通过接触性测量和非接触性测量[4-5],如膨胀式温度计、热电偶温度计、热电阻温度计、光学温度计、红外温度计和声波测温装置等。热电偶作为锅炉受热面温度测量最普遍测温元件,具有精度高、热容量小、使用方便、结构简单等特点,广泛地应用到锅炉各部位温度的监测,但复杂恶劣的炉膛火焰燃烧区域使热电偶易被烧损,故障率变高;对于热电阻测温元件存在抗机械冲击差、元件结构复杂、尺寸大、测温时间迟滞性等缺陷,限制了其应用范围。红外温度测量装置的核心部件为红外探头[6],由光学机构和光电探测机构组成,光电探头通过捕获红外辐射能量转变为精确的温度信号,由于燃烧器附近煤粉、飞灰颗粒造成光学辐射穿透力变弱、光谱变长,影响了红外探头测温的准确性。声波测温是锅炉监测精度较高的测温方式[7],但其较高的造价限制了其在锅炉各个部位温度监测的应用。目前接触式和非接触式电站锅炉温度监测方式都存在诸多不足,因此建立一种新型燃烧器壁温预测模型[8]对于锅炉自动控制有重要意义。
针对某650 WM 超临界电站锅炉等离子燃烧器壁温[9-10]存在超温、测点频繁故障,提出一种基于一维导热的壁温在线检测传感器模型,见图1 和图2,将表面包裹有绝热材料(忽略径向方向的导热)的金属杆埋设于装有等离子点火装置燃烧器的炉墙内,一端截面(热端)与燃烧器内壁表面平行。金属杆以一定的距离埋设有压电晶体测温探头,测温探头测得金属杆上每一位置的温度,通过分析金属杆上温度变化规律计算出远离高温区测温点温度与热端温度的对应关系。以传感器测杆内截面热端的温度代替燃烧器内壁表面温度,并与实际热电偶测得的温度进行校准。从而通过传感器冷端温度推测燃烧器内壁温度,在实际锅炉运行操控中达到保护测温设备和解决测温迟滞性的目的。

图1 传感器埋设
1 模型的建立
1.1 物理模型
图2 是传感器金属测杆热传递过程抽象示意图。对物理模型做出合理假设:
1)测温杆上包裹有绝热材料,热量沿轴向的方向传递,因此,假设该传热过程为一维导热模型;
2)在同一位置铁杆在径向方向温度均匀;
3)将燃烧器工况近似作为不同的稳定状态;
4)测杆的物性参数为温度的单值函数,并认定密度不变。
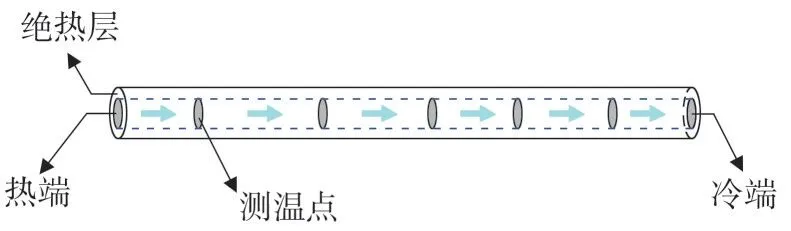
图2 传感器测杆热传递示意
1.2 数学模型
能量守恒方程
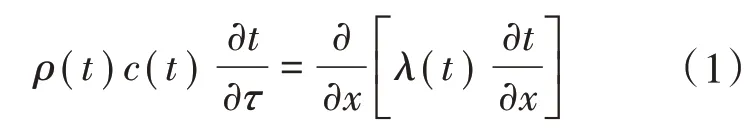
边界条件

式中:ρ为铁杆密度,kg∕m3;c为铁杆比热容,J∕(kg·K);λ为导热系数,W∕(m2·K);t为温度,K;h为对流换热系数,W∕(m2·K);ε为黑度;σ为玻尔兹曼常数,W∕(m2·K4);l为杆长,m;τ为热传递时间,s;tr为传感器热端温度,K;tl为环境温度,K;tf为冷端温度,K。
1.3 模拟参数
以铜质、铁质传感器测杆为例,本研究所涉及的变物性参数见表1,一律认定为温度的单值函数。非常物性参数导热系数λ、对流换热系数h随温度的变化关系为

自然对流换热系数h是温度的单值函数,当表面温度小于573 K(300 ℃)时,通过拟合对流换热系数与温度的对应关系得到


表1 物性参数
2 数学模型的实测验证
2.1 实测平台
对于模型的现场实测验证以铁质传感器测杆的验证为例。实测平台如图3所示,图中1、2、3、4为测温探头镶嵌位置取燃烧器壁筒一截面,在传感器测杆上共镶嵌有9 个测温探头,其热端嵌于燃烧器壁面,每个测温点与燃烧器壁面的距离L分别是0、4 cm、8 cm、12 cm、16 cm、20 cm、24 cm、36 cm、48 cm。测杆热端相同的轴向位置埋设热电偶直接测量燃烧器筒壁内表面温度,并以此对测杆热端温度加以修正。

图3 现场温度采集系统
2.2 实测验证结果分析
给测温程序赋初值,分别令热端温度为400 ℃(673 K)、500 ℃(773 K)、600 ℃(873 K),环境温度为300 K,当L=48 cm 的铁测杆上每一测温点都达到稳态后模拟温度分布与现场实测温度分布如图4所示。
图4 中模拟值与现场实测值在变化趋势上具有相似性,但具体某一测温点仍存在差异,所以对模拟值与现场实测值进行误差分析。
2.3 误差分析
如表2 所示,以873 K 工况下为例,对铁质测杆上测温点的实测值与模拟值进行误差分析,通过求两者间的相对误差反应模拟值偏离实验值的大小,如式(5)所示。

式中:δ为实际相对误差;Δ为绝对误差;β为真实值(实测值)。其中,Δ=∣L0-β∣,L0为模拟值。

图4 实测值与模拟值对比
以该方法求得该工况下的相对误差见表3。

表2 热端873 K工况下模拟值与实测值对比
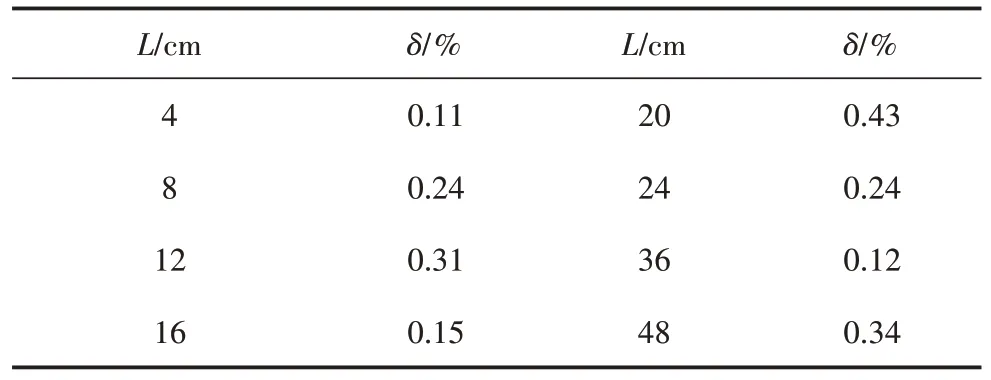
表3 热端873 K工况下测点相对误差
由表中数据可以看出,该工况下测点实测值与模拟值的相对误差均小于0.5%,对于热端另外673 K、773 K两个工况下的实际相对误差均小于1%。由于温度基数大,所以致使模拟值与实测值的相对误差值较小,所以实测值验证了数学模型是合理的。
3 数值模拟结果分析
以150 K的温变幅度为例,将铁质传感器测杆热端温度从1 300 K 提升至1 450 K 后L=4 cm、L=8 cm、L=18 cm、L=24 cm、L=36 cm、L=48 cm 处测温点温度变化曲线如图5 示,当曲线slop 斜率为0 时温度达到平衡。设测温点温度随时间的变化关系为

利用origin对图5的6条曲线进行拟合,以L=8 cm处的温变曲线为例得到拟合结果。

图5 铁质传感器测杆热端温度升高150 K后测温点温变趋势

图6 L=8 cm处测温点拟合结果
图6 为温变曲线拟合结果,图中拟合相关系数(R-Square)达到0.999 7,所以拟合精度较高,能够满足计算需要。拟合得到方程为

以相同的方法获取其他5 个测温点的温变曲线如下:

通过对式(7)—式(12)的方程式进行求导,并令导函数为0,即可获得测温点温度达到稳态的时间(即为响应时间),将响应时间带回式(7)—式(8)中,得到稳态温度如表4所示。

表4 热端升高150 K后测点稳态温度
由表4 拟合出热端升高150 K(此时热端温度升高至1 450 K)后各测温点稳态温度与其所在位置的对应关系式:

通过相同方法,在热端1 300 K 的温度,整个测杆达到稳态的状态下,将热端温度分别升高50 K、80 K、100 K、200 K、300 K 等5个温变工况,重复上述求解过程,获得不同热端工况下测杆上的温度分布如表4所示。
利用MATLAB 对表5 中热端稳态温度T与测温点稳态温度t、测温点稳态温度t与测温点位置x拟合得到复合函数关系式:

方程如下:

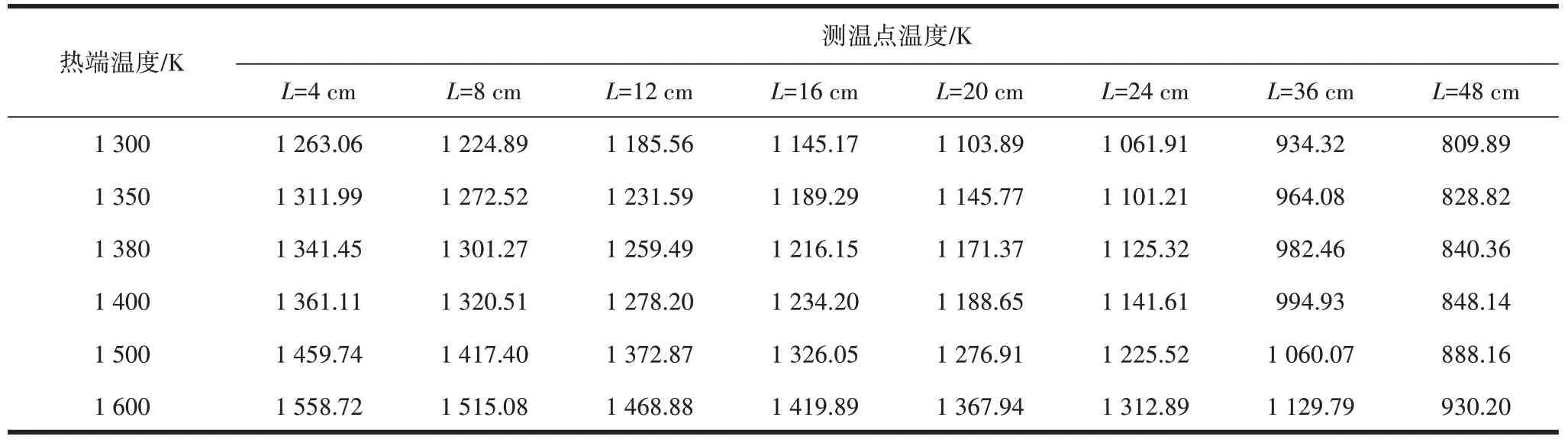
表5 不同的热端稳态工况下测温点温度分布

热端温度为1 300 K、1 350 K、1 380 K、1 400 K、1 500 K、1 600 K 6个不同工况时,测杆上每一测温点达到稳态后,不同节点位置x(测温点)与对应节点稳态温度t的回归方程如式(16)—式(21)所示,

同一测温点不同热端温度达到稳态后热端温度T与测温点温度t的回归方程如式(22)—式(29)所示,在传感器每一位置达到稳态后,利用测温点的稳态温度求得热端温度,不同测温点间相互校准,可对热端温度监测进一步修正,提高测温精确度。
上述回归方程在个别典型工况下计算所得,还需更多工况进一步完善。在实际应用过程中测杆上测温点温度未达到稳态工况,可获取一段温变曲线匹配图6 中的曲线进一步计算,若无变化可直接代入方程组中进行求解。
4 结语
传感器测杆热传输的过程的数值分析为测温传感器的实际应用提供了理论支持。其回归方程丰富了锅炉温度监测专家数据库。
壁温监测传感器能够解决测温迟滞性的弊端,能够第一时间给出燃烧器燃烧工况信息,能够为锅炉的自动化、智能化的控制提供新方法。
该传感器模型应用到实际生产过程中,能对测温设备形成有效保护,避免被炉膛火焰强辐射烧损。

