振动下惯性随钻测量的方位漂移闭环补偿∗

杨金显仝小森赵 淳王小康赵龙飞

(河南理工大学电气工程与自动化学院导航制导实验室，河南 焦作 454000)

近年来，集成加速度计/陀螺仪的MIMU 凭借其成本低、体积小、寿命长、抗冲击能力强和可靠性高等优势成为井眼轨迹的新兴测量方式，可以实现在磁干扰环境下精确随钻测量，在石油钻井、地质勘探、非开挖领域得到广泛应用，近几年逐步推广到煤矿领域，如煤层气抽采、底板加固等[1]。 目前，加速度传感器精度较高，可以获得较好倾角信息，但无法提供方位角信息[2]，陀螺仪存在器件精度问题，除此之外，地下工作环境复杂，随钻测量装置紧邻钻头安装，直接承受破岩、钻进的强烈振动干扰[3]，随时间累计产生较大误差，直接影响方位角解算精度，造成无法精确描绘钻孔轨迹，因此对在振动下的方位陀螺漂移补偿至关重要。

针对MWD 振动工作环境下陀螺误差引起方位角误差的问题，一是采用物理减振方式进行抑制，二是数学方法进行补偿解决，后者相对容易实施[4－8]。杨金显等直接利用重力四元数估计陀螺漂移并校正补偿，方位角误差减小到约0.46 °/h，结果表明该方法有效提高方位角精度[4]，但若倾角较小或接近90°时，方位角误差补偿效果变差；WANG 等构建一种基于开环算法的方位误差模型，补偿陀螺仪的Z轴漂移及尺度因子误差[5]，极大提高识别参数速度，但未考虑振动对姿态测量的影响；李杰等采用融合互补滤波和卡尔曼滤波的算法，以方位角误差和陀螺积分误差作为观测量来抑制陀螺漂移，处理后方位角测量精度控制在0.5°以内[6]；Zhang 等提出一种基于动态Allan 方差的陀螺误差模型[7]，使用卡尔曼滤波将外部辅助源引入模型，振动试验中方位角误差降低50%以上，但考虑到实际钻井中振动等干扰，方位测量精度还是较低；邵婷婷等应用神经网络的自适应调整参数特性，提出一种基于RBF 神经网络的算法来补偿校正方位角，最终方位角的测量精度提高至±1.9°以内[8]，但RBF 神经网络结构固定，实时性不强。

上述方法均可以提高随钻工作中钻具方位角的姿态测量精度，但在应用中通常忽略井下环境的振动因素对传感器的不利影响，可适用于低频振动环境，若噪声模型实时性不强，强振下难以适用；另外RBF 初期学习速度慢，难以适用时变复杂对象，会有很大的限制性。 鉴于传感器除自身误差外，易受到振动环境影响，导致方位姿态不准确。 因此，提出一种基于MIMU 的随钻方位角测量方法，利用多传感器分布式信息融合，根据测量加速度与重力加速度在钻具坐标系下的向量误差，建立振动加速度存在下的方位陀螺漂移PI 控制模型，且设计一种基于多组Taylor 展开式的新型神经网络结构，辨识方位陀螺误差特性，通过优化权值直接确定法OWDD 快速辨识该网络权值，PI 控制器根据该网络的辨识结果，实时补偿方位陀螺漂移，实现振动下的方位长时测量。

1 惯性随钻方位漂移补偿模型

1.1 惯性随钻方位漂移

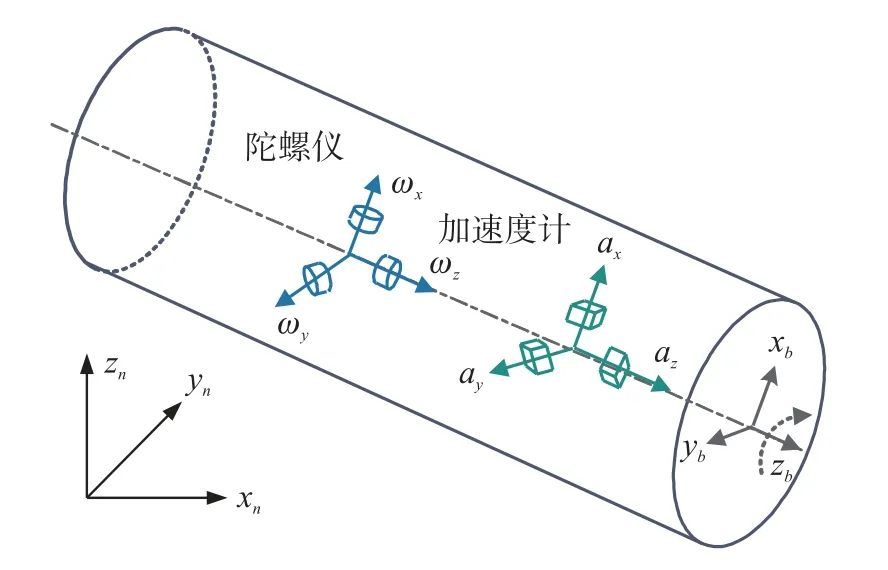
目前，在磁干扰环境下MWD 系统借助加速度计/陀螺仪测量方位角成为一种新型测量方式[9]。惯性测量装置通常需要提供准确的姿态信息以便于进行井眼轨迹控制，主要为方位角、倾角和孔深，其中孔深由钻杆控制，倾角由加速度计测量，而方位角的测量最为复杂困难。 传统控制方位角的方法有经验估计、陀螺仪定姿[10]，如果根据钻进经验来估计，会有很大的不确定性，而陀螺仪数据长时间工作会产生较大的累积误差致使方位角解算精度不高，因此需要辅助传感器。 目前加速度计精度较高，但会受到钻进时振动干扰而产生偏差，需要考虑加速度数据带有振动；MEMS 陀螺仪由于制造工艺和设计水平的局限性，在振动冲击时的测量精度较低，其误差主要为确定性误差和随机漂移误差，前者通过标定解决，后者通过建立测量模型从而进行误差补偿[11]。 在工程上，在现有惯性器件精度的基础上，利用算法来提高系统测量精度是最为有效的办法之一[12]，因此利用加速度计对强振下的陀螺仪误差进行建模补偿，进而提高方位角测量精度。

MEMS 陀螺仪的测量模型为:

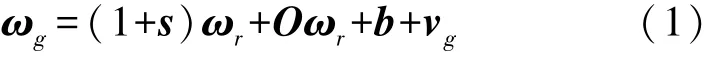
式中:vg为高斯白噪声，s、O、b分别为标度因数误差、非正交误差和零偏误差，这些确定性误差均可通过实验标定进行校正，整理后其输出模型为:

式中:ωg＝[ωxgωygωzg]T为陀螺仪的测量值；ωr＝[ωxrωyrωzr]T为角速度真值；bg为陀螺漂移。

MEMS 加速度计的输出模型为:

式中:aa＝[axaayaaza]T为加速度计测量值；ag＝[axgaygazg]T为重力加速度在钻具坐标系下的投影；a＝[axayaz]T为振动加速度；va为高斯白噪声。

上式中的bg、vg直接影响方位角的解算精度，vg可通过预处理来消除，bg很难直接估计并补偿，考虑到加速度计测量误差无累加，因此借助加速度传感器对陀螺仪数据进行修正。

重力加速度经坐标变换在钻具坐标系下投影:

但是在随钻强振动环境下，向量aa与ag的叉乘值是由陀螺漂移和强振动引起的，因此，在利用测量加速度和估计加速度的叉乘项进行闭环控制补偿时，需要考虑振动特性。

1.2 振动下的漂移补偿模型

对于姿态、角速度偏差可通过PD 控制快速调节[13]，而往前钻进属于低速过程，对快速性要求不高，尤其当误差较稳定时，PD 控制就会失效；而随钻测量主要对测量精度要求高，辅助传感器加速度计性能较好，但加速度数据带有振动参数，因此采用PI 控制来调节向量误差，建立方位陀螺漂移补偿模型。 思路是调节向量误差对方位陀螺漂移进行全补偿，再用补偿后的陀螺仪数据解算出精确方位角，整体流程如图1 所示。

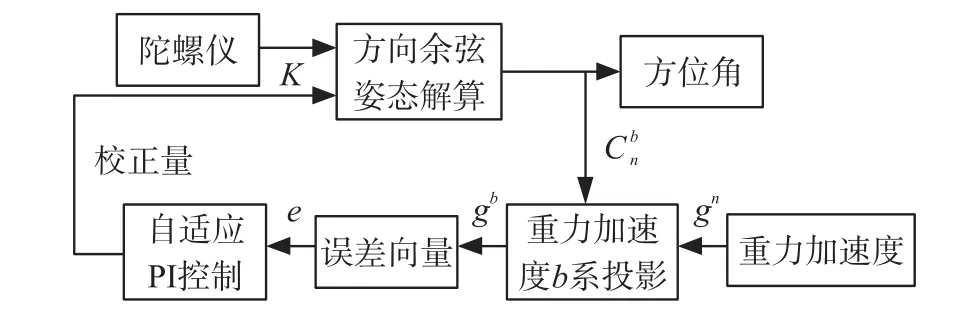
图1 方位漂移闭环补偿流程图

预处理后的角速度为:

式中:n为一周期的采样次数，s为PI 控制器输出，Q1＝1/(1－k2K)(1－k3K)、Q2＝1/(1－k1K)(1－k3K)、Q3＝1/(1－k1K)(1－k2K)为三轴振动调整系数。

式(9)即随钻振动环境下方位陀螺漂移的数学模型，根据随钻测量多传感器系统的四元数可解算出当前时刻的方向余弦矩阵，则对ex、ey、ez不同取值的控制，可达到补偿方位陀螺漂移的目的。

2 控制参数辨识

2.1 神经网络模型构建

由上节知kp、ki的识别精度决定方位陀螺漂移的补偿程度，因此为实现方位角的准确控制，设计漂移补偿控制系统，一是通过建立一种基于多项式逼近的新型神经网络结构，准确辨识惯性随钻测量系统的方位陀螺漂移，确定神经网络的输出层权值；二是基于系统辨识结果，根据输出值，得出合理PI 控制量补偿方位陀螺漂移，实现方案如图2 所示。

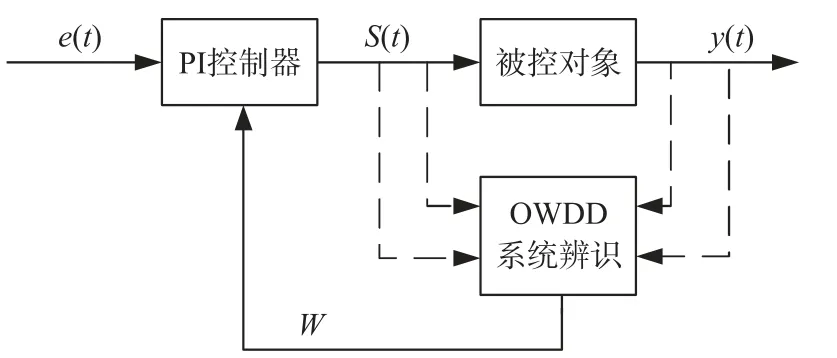
图2 控制系统结构

由于工作时钻头往前钻进速度较慢，实时性要求不高，且考虑到振动导致的非线性、漂移非线性和时变性，设计一种神经网络在线辨识算法，利用神经网络控制复杂非线性的方位陀螺漂移，引入函数逼近理论学习随钻测量系统的不确定动态特性，且基于矩阵伪逆思想，一步确定网络权值，实时快速整定PI 控制参数，跟踪误差变化趋向，大大减少计算量，快速有效地补偿方位陀螺漂移，满足随钻控制的要求。

随钻测量系统工作时，方位陀螺漂移具有时变非线性特点，对于这种难以表达的复杂函数，构建神经网络对其进行分析的过程，就是用很多函数构造的函数网去逼近非线性模型，计算近似值[14].在随钻系统开始工作时，陀螺仪t＝0 时刻，输出y＝0，此时瞬时角速度准，无累积误差，控制量s＝0，根据多项式函数可以接近任意函数，已知PI 控制器输出函数s(t)在某一点的各阶导数值的情况之下，泰勒公式可以用这些导数值做系数构建一个多项式来逼近函数在这一点的邻域中的值。 因此根据式(9)～式(14)可推导方位陀螺漂移控制量s(t)的值，若f(x)在x＝0 具有任意阶导数，则可展开成在x＝0 的泰勒级数:

式中:Na为函数a(s)的泰勒展开式项数，Nb为函数b(y)的泰勒展开式项数，Nm为系统的控制区间，R为输入输出函数麦克劳林级数余项在Nm区间内总和。

根据式(16)建立一种适用于复杂随钻环境的新型神经网络模型，其由输入层、隐含层、输出层三部分组成。 输入层有2Nm－1 个神经元，对应t－Nm＋1 到t－1 时刻的方位陀螺漂移控制量s、t－Nm＋1 到t时刻的目标角速度输出值y，隐含层有n(Nm－1)＋mNm个神经元，输出层为1 个神经元，对应t时刻的控制输入量s，其结构如图3 所示，采用优化算法确定其网络权值，最后基于系统辨识结果，PI 控制器对方位陀螺漂移进行补偿。

图3 新型神经网络结构

从图3 可以看出，网络输入层、输出层均采用线性恒等激励函数，隐含层采用一个输入层单元对应一组阶次逐渐增高的幂函数，且为后续一步确定权值做准备，整个网络神经元阈值取零。

2.2 漂移参数辨识

考虑随钻振动环境下方位陀螺漂移的误差特性，自适应调节PI 控制器参数，控制误差补偿，需要辨识上述神经网络权值。 为改善神经网络前期学习速度慢，不适应时变强非线性系统，致使系统误差大的问题，需要在辨识样本区间Nn范围内一步确定输出层权值W，因此设计优化权值直接确定法OWDD 快速确定辨识方位陀螺漂移对象的神经网络权值，实现快速准确控制方位陀螺漂移的目标。该控制系统误差评价函数为:

式中:Y＝[S(t－1)S(t－2) …S(t－Nn)]′为神经网络输出值；X＝[XuXy]为隐含层神经元。

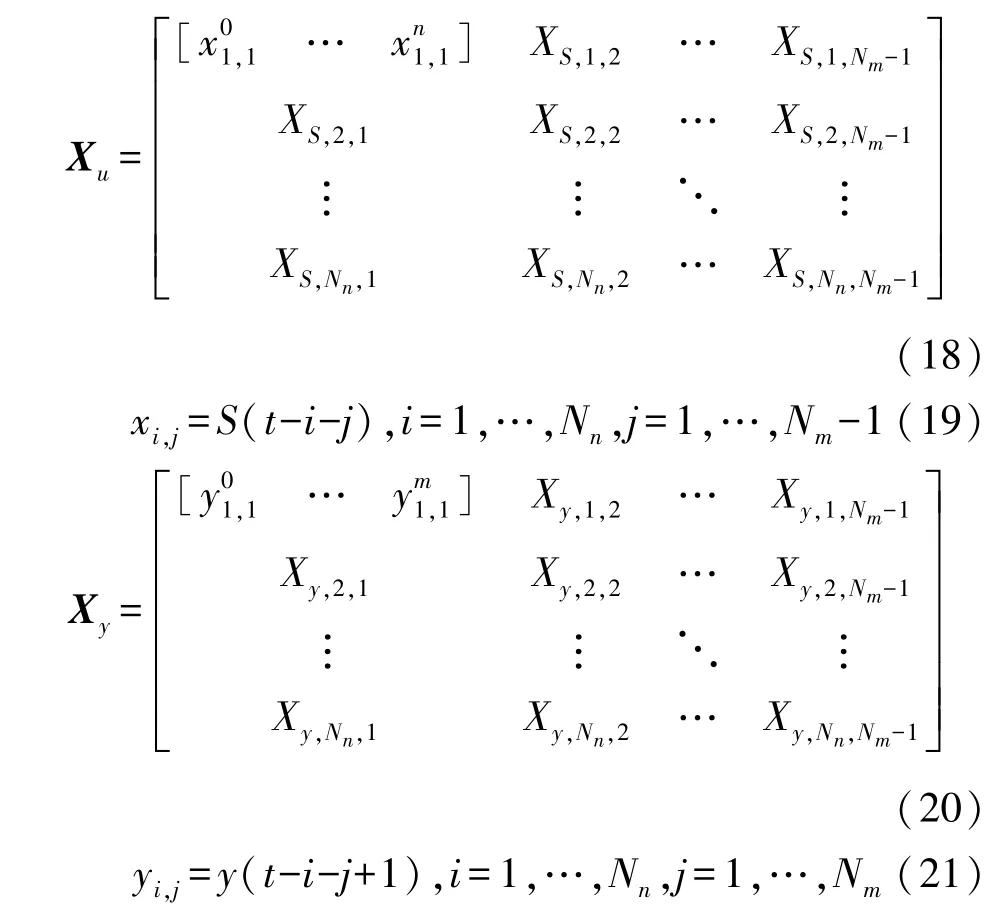
W＝[W1W2…WNn]′为隐含层到输出层权值，Wi＝[WSWy]′，i＝1，…，Nn；其中:

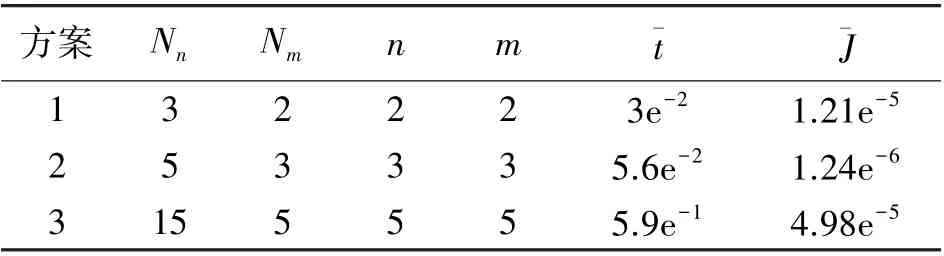
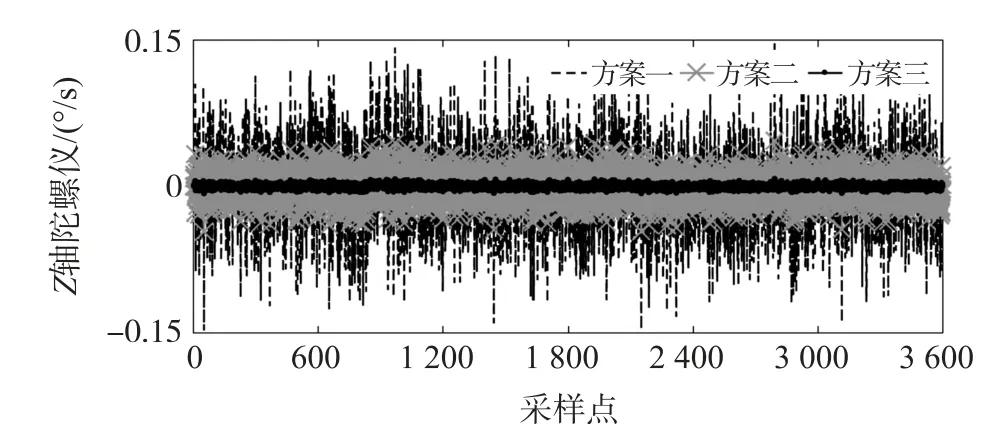
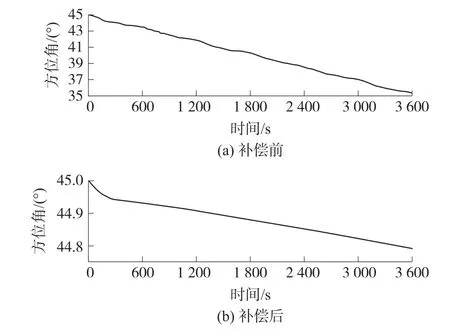
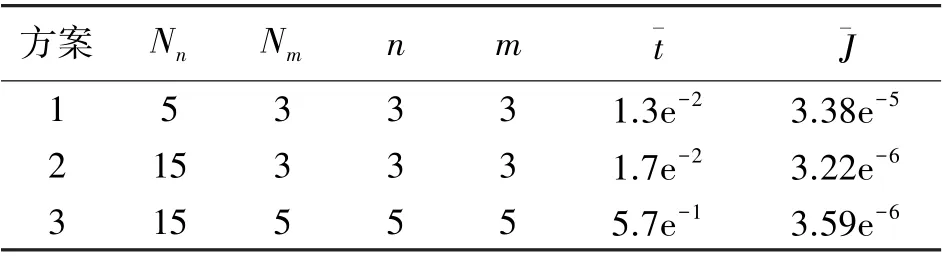
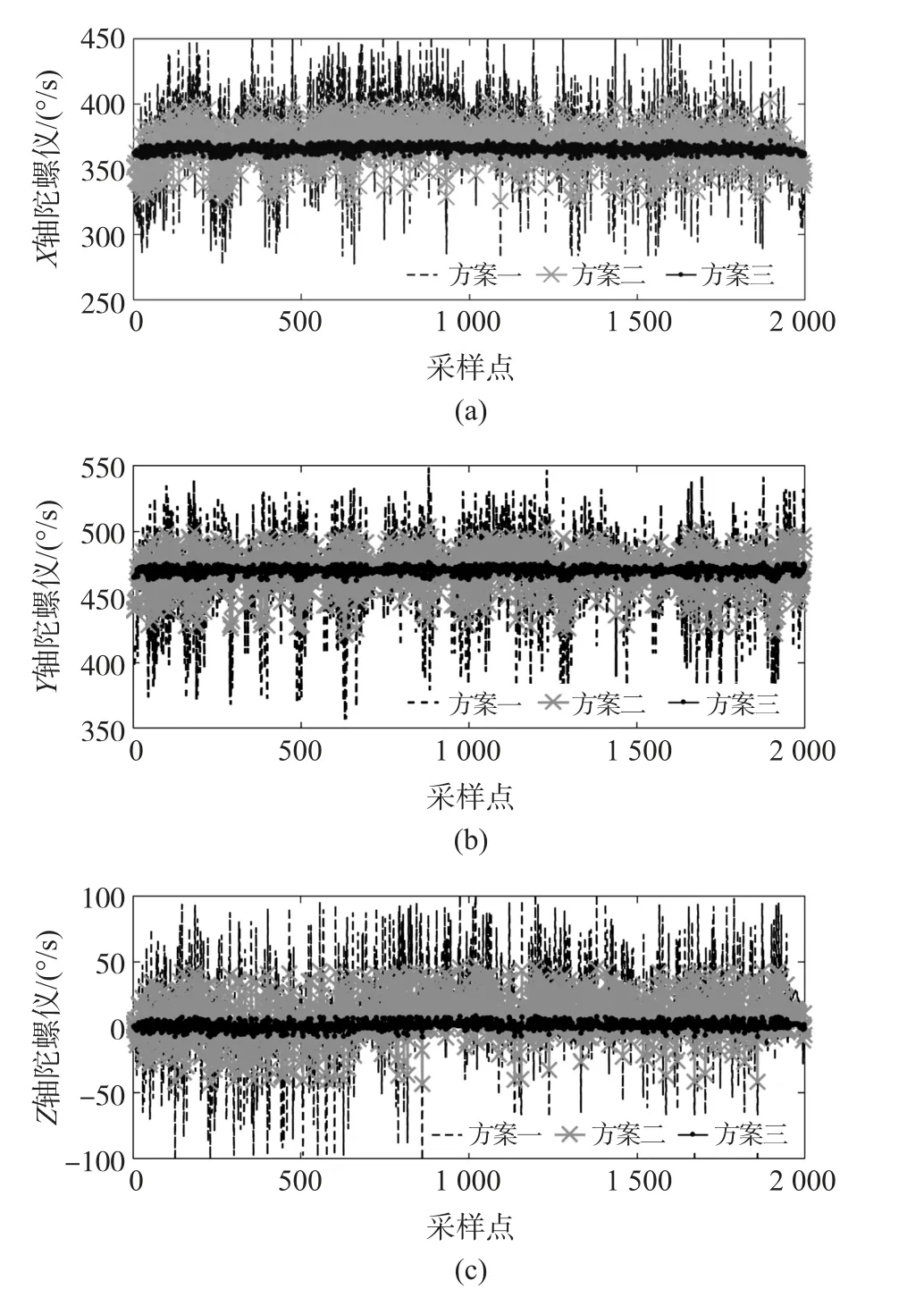
由于定义的前提条件是单调区间，因此满足Nn

其中，Xc＝[XcSXcy]为隐含层神经元输入量，

3 实验与分析

为对本文设计的方位陀螺漂移闭环补偿方法进行充分验证，利用实验室研制的蓝牙惯性随钻装置进行实验，该装置由三轴加速度计和三轴陀螺仪组成，技术参数如表1 所示。

表1 随钻测量装置技术参数

实验场地条件为北纬35°，东经113°，地球自转角速度15 °/h，地球重力加速度为9.8 m/s2。 选取地理坐标系(东－北－天)作为导航坐标系(n系)，指向东，指向北，指向天；钻具坐标系(b系)用表示，MIMU 的安装位置如图4 所示。

图4 MIMU 安装示意图

3.1 振动台实验

在室温条件下，将标定后MIMU 固定在LD-PTP电磁振动台上，如图5 所示；调节振动控制仪将振动台倾斜角设置为45°，并设置振动台沿Z轴垂直(上下)随机振动，频率为10 Hz；振动台稳定后持续采集1 h 的陀螺仪数据。

图5 振动台实验

记录静态初始姿态，初始化条件y0＝0，s0＝0；根据随钻方位陀螺漂移误差特性，选取该模型辨识样本数Nn、多项式项数Nm、输入输出函数泰勒展开式项数n、m，仿真的具体数据如表2 所示。

表2 振动台实验模型参数

从表2 可知模型参数的不同取值，直接影响控制精度。 随着辨识样本数Nn、多项式项数Nm、输入输出函数泰勒展开式项数n、m增大到一定程度，控制精度会有个最大值，参数继续增大，控制精度却逐渐减小，由此选取合适模型参数进行控制至关重要。为了直观地描述所设计算法对误差的补偿效果，选取Z轴陀螺仪的3 600 组数据绘制不同方案补偿前后MEMS 陀螺仪角速度曲线如图6 所示。

图6 振动台实验不同补偿方案陀螺角速度的输出

为了进一步验证结果的准确性，由前文分析可知，方位陀螺漂移控制量s的估计，依赖所设计的神经网络权值W的确定。 实际应用中，已知模型辨识样本Nn＝5、多项式项数和输入输出函数的泰勒展开式项数Nm＝n＝m＝3 时控制效果最好，按照2.2小节的优化算法辨识网络权值，PI 控制器将基于系统辨识结果，根据目标输出值，计算出方位陀螺漂移的最佳控制量，此时得到补偿效果最好的方位角输出，如图7 所示。

图7 振动台实验最佳方案补偿前后陀螺方位角对比

由图7 可以看出，算法补偿前后方位角误差由由10.15 °/h 减小到0.21 °/h，可以看出方位角误差明显减小，说明算法在振动加速度存在时能较好补偿方位陀螺漂移。

3.2 实钻井实验

为进一步验证惯性随钻测量方位角补偿效果的现场实用性，选择焦作某煤矿的钻进测试数据进行实验验证，考虑到随钻方位陀螺漂移误差特性，选取该模型辨识样本数、多项式项数、输入输出函数泰勒展开式项数取值如表3 所示。

表3 实钻井实验模型参数

根据实际钻井数据，利用算法实时估计并补偿方位陀螺漂移，为了便于描述不同参数对钻进实验中对方位角补偿效果的影响，选取MEMS 陀螺仪的2 000 组数据绘制不同方案补偿前后陀螺仪的三轴角速度曲线如图8 所示。

图8 实钻井实验不同补偿方案陀螺三轴角速度的输出

从表3 和图8 可知，已知模型辨识样本Nn＝15、多项式项数和输入输出函数的泰勒展开式项数Nm＝n＝m＝3 时控制效果最好，对比算法控制补偿前后的方位角输出，如图9 所示。

图9 实钻井实验中最佳方案补偿前后陀螺方位角对比

通过前述流程计算相应的控制量，补偿前后方位角误差10.53 °/h 减小到0.3 °/h 之内，可以看出钻具的方位角误差明显减小，进一步验证本文提出的惯性随钻测量的方位角补偿方法可以有效的提高钻具方位角测量的精度。

4 结论

针对振动下随钻测量方位角失真的问题，本文提出一种基于MIMU 的方位角闭环补偿方法.首先由加速度计、陀螺仪的角速度、加速度数据，构建测量加速度与重力加速度在钻具坐标系下的向量误差，分析方位角误差特性，建立振动加速度存在下的方位陀螺漂移PI 控制模型，设计一种基于多组Taylor 展开式的新型神经网络和优化权值直接确定法OWDD，在线辨识参数以控制PI 控制器补偿方位陀螺漂移的效果，最终得到精确方位角。 为验证算法有效性，设计振动台实验，其方位角误差由10.15 °/h 减小到0.21 °/h，实现对方位陀螺漂移的补偿；通过实际钻井实验，发现钻进过程中方位角误差由10.53 °/h 减小到0.3 °/h，方位角的测量精度明显提高，综上说明本文提出的随钻测量方位角闭环补偿方法具有很好的应用效果。