颗粒物质力学及其在工程地质领域中的应用初探*
郑 虎 牛文清 毛无卫 李丽慧 汪发武 黄 雨
(①同济大学地下建筑与工程系,上海 200092,中国)(②同济大学岩土及地下工程教育部重点实验室,上海 200092,中国)(③中国科学院地质与地球物理研究所,北京 100029,中国)(④中国科学院地球科学研究院,北京 100029,中国)(⑤中国科学院大学,北京 100049,中国)
0 引 言
绝大多数地质体(如松散堆积体、砂土、砾石等)属于颗粒物质,颗粒物质是由大量离散颗粒组成的复杂无序体系(Jaeger et al.,1996;孙其诚等,2017),堆积时类似固体,流动时类似液体,但是其液、固态性质都与牛顿流体、弹性固体等连续介质体系有着显著的差别。颗粒物质在静止堆积状态到运动演化过程中所表现出的特有力学现象,是近几十年来在不同尺度(微观、介观、宏观)进行系统研究的科学问题(Bi et al.,2011;Wang M M et al.,2019)。颗粒材料一般指单个颗粒尺寸大于1μm的离散颗粒固体组成的宏观物质体系,是地球上存在最多,人们最为熟悉的物质之一,广泛存在于日常生活(食品的加工)、农业(谷物的储存和运输)、医药科学(药剂的混合)、工业生产(矿石的分选与传输)和地质科学(滑坡、泥石流、雪崩、地震、火山碎屑流)中(王瑞琪等,2019;郑光等,2019;王高峰等,2020)。这些领域中均面临着大量的颗粒材料相关问题和难题,因此研究颗粒材料力学性质具有重要的实际意义。
对宏观颗粒物质而言,当颗粒尺寸较大时,可以忽略温度的影响,传统的热力学影响忽略不计,在没有外界扰动的情况下,颗粒介质自发地运动可以忽略不计。颗粒体系为能量耗散体系,颗粒运动的能量通过颗粒之间的摩擦和碰撞而耗散掉(Jaeger et al.,1996)。早期一些学者主要运用动力学理论和塑性模型分别描述快速流和准静态流(Garzo et al.,1999)。当惯性系数小于10-3时的颗粒流动可以看作为准静态流动,产生的应力与运动状态无关。当施加的剪切强度较弱,所研究的体系由密实的颗粒组成时,颗粒间运动相对缓慢或静止,假定它们遵循库仑摩擦定律,并使用塑性理论进行建模(Jackson,1983)。与此相反,快速颗粒流的惯性行为所产生的应力与剪切速率呈二次方变化。在快速剪切的情况下,松散的颗粒系统甚至可以表现出类“气体”的随机碰撞,此时颗粒被类比为气体动力学中的分子,并被假定为热运动和瞬时碰撞的相互作用(Campbell,1990)。
在20世纪80年代末,Edwards(1990)提出了具有开创性的颗粒介质热力学,为准静态流动提出新的物理概念。颗粒物质的力学稳定态与力学非稳定态转化——阻塞相变逐渐成为软物质物理的研究热点。Liu et al.(1998)用阻塞相变图描述了颗粒物质阻塞相变转化,当颗粒物质的体积分数足够大时才会发生阻塞,进入力学稳定态。可以通过施加应力或减小颗粒系统的体积分数来破坏阻塞状态,当考虑到温度的影响时,也可以通过升高温度来破坏系统的力学稳定状态。Bi et al.(2011)对Liu-Nagel 相图做了修改,提出了包括一个有限剪应力下摩擦颗粒材料的剪切阻塞(Shear Jamming,SJ)区域。Chialvo et al.(2012)研究了摩擦颗粒物质阻塞相变转化,并讨论了准静态、惯性和过渡态体系流变模型的构建。Zhao et al.(2019)利用一种新型的库埃特多环底部剪切装置,扩展了颗粒材料的剪切阻塞相图。颗粒介质与经典弹塑性材料相比,具有显著的离散性,只有对颗粒材料内部物理变形过程、变形机制、失稳机理和能量耗散有一个较为清晰的认识,才能建立科学合理的本构关系(李广信,2006;孙其诚等,2009,2011)。
工程地质领域中许多地质灾害现象的本质即为颗粒材料自身相态的转化,比如,滑坡、泥石流其实就是颗粒材料由固相(力学稳定的Jammed状态)向液相(力学非稳定的Unjamming状态)的转化。颗粒物质力学的研究能提高对泥石流、滑坡、地震等地质灾害诱发机理的认识(孙其诚等,2008)。在过去的30年里,物理学家对颗粒介质主要利用统计和流体动力学方法将类似流体、依赖于速率的流动方法与适当的屈服准则结合起来研究颗粒体系复杂的流动规律(Jaeger et al.,1996;Henann et al.,2013)。力学和材料科学人员从土力学的角度,基于连续体固体力学的原则,采用各种屈服准则和塑性流动关系来建立颗粒材料流动模型(Nedderman,1992)。许多学者对干颗粒流做了大量研究,假设颗粒间的流体不起任何作用,这种流变主要受颗粒间的摩擦和碰撞作用所控制。Iverson et al.(2004)考虑到尺度的影响,用微型实验来测试流体和黏聚力的影响可以忽略不计的颗粒崩塌模型,模拟了复杂自然地形的不规则基底上发生的干颗粒崩塌行为,实验采用了一种新型的激光辅助制图方法来绘制快速流动雪崩的三维形态,该模型不仅能准确地预测雪崩的总体行为,而且能准确地模拟崩塌从发生到堆积的运动过程。
颗粒物质力学对颗粒物质在不同运动状态下的相变转化、颗粒流变等方面已取得了一定的研究成果,研究注重机理和理论分析,相关的研究成果不易直接应用到解决具体工程地质问题中。目前,在工程地质领域已有许多针对工程地质问题的颗粒流研究成果,但多数研究成果为将地质体简化成离散颗粒体系并通过颗粒流离散元数值模拟开展的,真正意义上将诸如颗粒物质相变及颗粒流变等颗粒物质力学应用到工程地质领域内的研究并不多见。通过开展颗粒物质力学与工程地质的交叉融合研究,有望拓展颗粒物质物理与力学的研究深度和应用价值,同时也可以为重大工程及地质灾害防治的研究提供理论基础。
1 颗粒物质基本性质
在古代,人们就开始关注颗粒物质的运动规律,利用开口处流出的沙粒流量能保持一个相对稳定的状态,发明了作为计时的工具——沙漏。颗粒流模型始于1773年法国物理学家库伦(Coulomb)第1次把颗粒材料的屈服描述为摩擦过程,提出了库仑摩擦定律。1831年,英国物理学家Faraday发现在装有颗粒的圆柱形容器中,受到垂直连续的振动力后,颗粒发生了对流现象。1884年,英国科学家Roberts观察到当粮食堆积高度大约超过两倍的底面直径后,粮仓底面压力不再一直增大而是趋于饱和,这与容器中液体压强随着深度增加而增加的性质完全不同。随后,德国工程师Janssen从连续介质理论出发提出了Janssen模型,解释了粮仓效应(Janssen,1895)。同期,Reynolds发现颗粒紧密堆积,施加外力作用使得颗粒体系体积增大,称为挤压膨胀现象(Reynolds,1885)。
颗粒体系中单个颗粒受力特性可以通过固体力学解释,而对于堆积的颗粒体系而言,休止角是一个与颗粒摩擦力相关描述颗粒基本性质的重要参数之一。休止角现象是指颗粒堆积体相对于水平面可以保持静止的一个有限角度。在实际应用中,休止角可以在沙堆失稳前取一定范围的值,在崩塌发生之前存在一个最大稳定角。由于沙堆是一个非热体系,所以具有很强的滞后特性,导致了沙堆表现出双稳性,使得沙堆可以在休止角和最大稳定角间任意角度范围内保持稳定或运动状态(Mehta et al.,2001)。颗粒材料堆积时内部的应力、对地面的压力也是人们一直关注的问题。点源法形成沙堆中心对地面的压力不是最大的,压力分布函数在中间位置有一处凹陷,而落雨法形成的沙堆不存在应力凹陷,这说明应力分布与堆积历史有关(Wittmer et al.,1996)。对颗粒堆积体系施加外力作用,堆积密实的颗粒体系会变得体积膨胀,堆积密度变小,即挤压膨胀现象(Reynolds,1885)。粮仓效应从侧面揭示了颗粒体系内部特殊的应力分布,促使人们希望通过实验研究颗粒体系内部力的传递方式。
颗粒材料的动力特性也一直备受关注,当两种大小不同的颗粒混合在一起,受到振动作用后,会发生分离,一般是大颗粒在上,小颗粒下沉到底部,称为巴西果效应。但后来又发现与之相反的反巴西果效应,体积大的颗粒下沉而体积小的颗粒上升,这两种效应至今也是颗粒物理学一个非常热门的话题之一(Walliser,2002)。Jmnt(1997)对颗粒崩塌过程中的流变行为进行了研究,发现双分散相颗粒混合物运动筛分,会产生两层剪切带,其中大颗粒覆盖小颗粒。此外,由于雪崩表面运动速度快于底部,大颗粒被输送到前方,而小颗粒则集中在雪崩的后部。垂直振动下颗粒表面会形成斑图,根据所应用的振动条件,在干燥振动颗粒床中可以观察到周期性的形成六边形、条纹或蜂窝状图案。在振动颗粒床中形成的图案可能是二维牛顿摆效应的结果(Eldin,2014)。振动分选是颗粒物质一个重要性质,与工程地质领域里高位远程滑坡后堆积出现的大颗粒物质出现在表面极为类似。
20世纪80年代末,物理学家使用统计力学来研究颗粒介质,颗粒物理领域迅速发展起来。颗粒体系是复杂系统,表现出亚稳态、滞后、双稳性和一系列其他独特的现象。2005年,在庆祝Science 创刊125周年之际,该杂志公布了目前世界上最具挑战性的科学问题,其中将“能否发展关于湍流动力学和颗粒材料运动学的综合理论”和“颗粒物质的非平衡态动力学理论”列为其中,成为软物质物理学和应用学科(如地质、工业、医药等)交叉领域的前沿热点之一。
2 颗粒物质剪切流动特性
即使对于干燥且无黏性颗粒体系而言,颗粒组合的行为也极为复杂。而当颗粒足够大,且周围流体黏性较小时,颗粒间的相互作用以接触作用为主,通常情况下也会忽略颗粒间的毛细压力、范德华力或黏性等相互作用,假设颗粒间的力学性能仅由颗粒间碰撞或摩擦接触时的动量传递来控制(MiDi,2005)。颗粒流流动可以依据颗粒的流动速度划分为3个不同的体系状态:准静态、过渡态、稀疏流态。在准静态体系,颗粒的惯性可以忽略,整个颗粒体系可以看作是连续的固体,可以用土的塑性模型去描述(Nedderman,1992;Campbell,2006)。对于稀疏态颗粒流,可以通过二元碰撞相互作用类比描述其运动特征(Goldhirsch,2003)。然而,对于中间过渡态,颗粒状物质可以表现得像液体一样流动。颗粒体系的固态与液态转化以及其流变特性也是目前颗粒物质领域内研究的重要科学问题之一。
2.1 颗粒物质阻塞相变与剪切阻塞相变
颗粒堆积体从液相到固相的相态转化涉及到许多不同的领域,如工程地质中的岩土松散体的失稳流动破坏、悬浮液的剪切稀化与剪切增稠或非连续剪切增稠、玻璃金属、玻璃态等(Zheng et al.,2014;Chen et al.,2019;Wang B D et al.,2019)。Gate et al.(1998)提出颗粒体系阻塞状态与普通固体不同,如果施加的应力方向发生了很小的变化,那么阻塞就会被破坏,沙堆就是一个典型的例子,基于这个模型可以认为阻塞的颗粒体系不是一个弹性体。虽然它可以在起初阻塞状态力链同一方向上支持一个大的施加的负荷,但是一个无限小的力施加在不同的方向,力链颗粒会发生破坏导致颗粒体系溃散。Liu et al.(1998)认为,处于阻塞状态的颗粒材料类别实际上可能更广泛。不考虑温度的影响,对于非热系统的阻塞状态只存在于一定的临界密度(φJ)以上,增加体积分数会导致颗粒系统进入阻塞状态并且在屈服应力线上剪切应力(τ)可导致不可逆的流动发生。而当颗粒尺寸足够小,考虑到温度的影响,也可以通过提高温度使得颗粒系统由阻塞状态过渡到未阻塞状态(图1),阻塞相图得到广泛应用并吸引了大量学者进行理论研究和数值模拟。
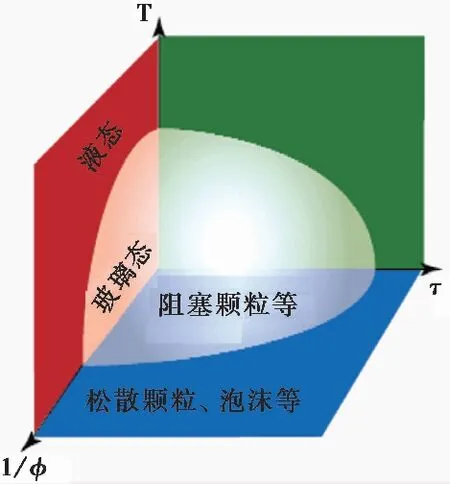
图1 阻塞相变图(Liu et al.,1998)Fig.1 Jamming phase diagram(Liu et al.,1998)
图2a为不考虑温度影响时(T=0)Liu-Nagel阻塞相图,增加体积分数(φ)可达到阻塞状态,若剪应力(τ)越过屈服线系统又会进入流动状态。虽然对无摩擦颗粒的数值模拟大体上支持Liu-Nagel阻塞相变观点,但是摩擦颗粒的阻塞相变却表现出不一样的现象,特别是在当整个颗粒体系发生剪切变形后。Bi et al.(2011)发现在体积分数低于临界体积分数一定范围时,若整个颗粒体系发生剪切变形后,即使在不改变系统体积分数的情况下,颗粒体系也会由未阻塞状态进入阻塞状态,称为颗粒物质的剪切阻塞,并在Liu-Nagel阻塞相变图上填补了重要的区域,如图2b所示。该区域的填补对颗粒材料剪切研究,特别是宏观世界中所遇到的具有摩擦力的颗粒系统的研究具有极为重要的意义。
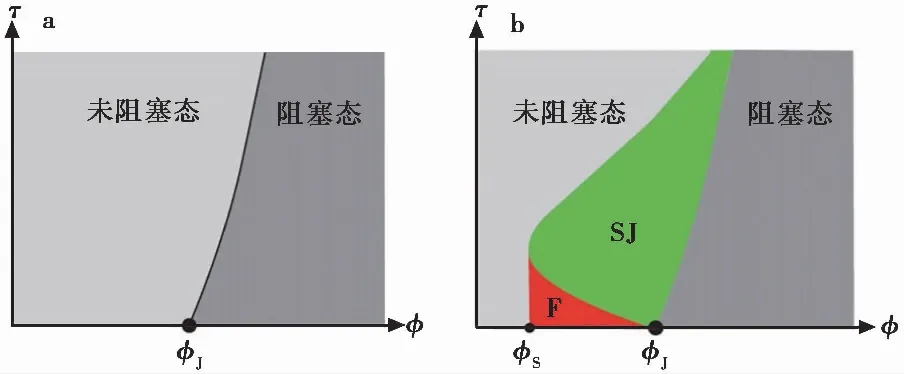
图2 T=0平面的阻塞相图(Bi et al.,2011)Fig.2 Jamming phase diagrams in the T=0 plane(Bi et al.,2011)
2.2 颗粒物质局域流变
对于颗粒物质流动特性的描述至今仍是软物质物理里研究难点之一,颗粒系统内部的剪应力和抗剪强度是导致颗粒物质发生流动的决定性因素,若颗粒系统内部的剪应力超过临界剪应力时系统则会流动,颗粒体系进入未阻塞状态,展现出流体的特性,反之则不会流动,这与经典的黏塑性流体有相似之处。Jop et al.(2006)通过对前人的数值模拟和实验总结,提出了描述密集流态的颗粒流动本构模型,在不引入拟合参数的情况下,该本构模型可以很好地预测颗粒流动过程中的形状和速度分布,且可以定量地描述颗粒流动特性,并应用于地球物理或工业中模拟更复杂的流动。
在地质工程领域及工业界常遇到颗粒物质在倾斜表面上的流动问题,例如高位滑坡碎屑流、矿物和谷物等材料的运输等。颗粒流动的特性主要由颗粒自重、颗粒与颗粒及颗粒与边界摩擦力的平衡所控制。描述密集颗粒流的难点在于它属于中间过渡态流型,其中颗粒间的摩擦和碰撞都起着重要作用。Pouliquen(1999)对玻璃微珠沿粗糙倾斜表面的密集均匀稳定颗粒流进行了系统的试验研究,测量了平均流速作为表面倾斜角θ和最小流动层厚度hstop(θ)的函数(图3),发现Froude数和归一化后的流动层厚度h/hstop(θ)呈线性关系:
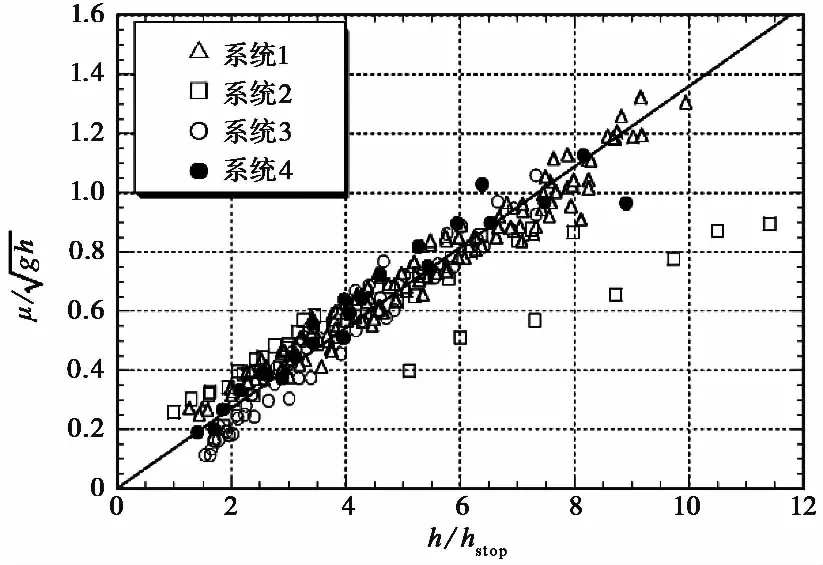
图3 4个系统不同倾角下Froude数和h/hstop(θ)函数关系(Pouliquen,1999)Fig.3 Froude number as a function of h/hstop(θ) for the four systems of beads and for different inclination angles(Pouliquen,1999)
(1)
式中:u为颗粒流动速度;β为与颗粒摩擦性质相关的参数;g为重力加速度;h为颗粒流动层厚度。
平面剪切试验是密集颗粒流最常用的试验方法之一,试验过程中两个粗糙边界之间在正应力P约束下,通过施加剪应力τ,对颗粒材料进行剪切。Da et al.(2005)通过量纲参数分析和数值模拟,首先定义了摩擦系数(μ),并发现了密集颗粒流动过程中剪应力与法向应力成正比,比例系数为单一无量纲数的函数,这个无量纲数称为惯性数I:
(2)
(3)
Pouliquen(1999),Pouliquen et al.(2002)通过对比平面剪切试验和沿粗糙斜面上的斜槽流实验,揭示了摩擦系数μ和惯性常数I之间的单调函数关系(图4)。摩擦系数存在一个门槛值(μs),并随着惯性常数增大,最终趋近于一个最大值μ2。Jop et al.(2006)提出了与此实验现象相符的摩擦定律:
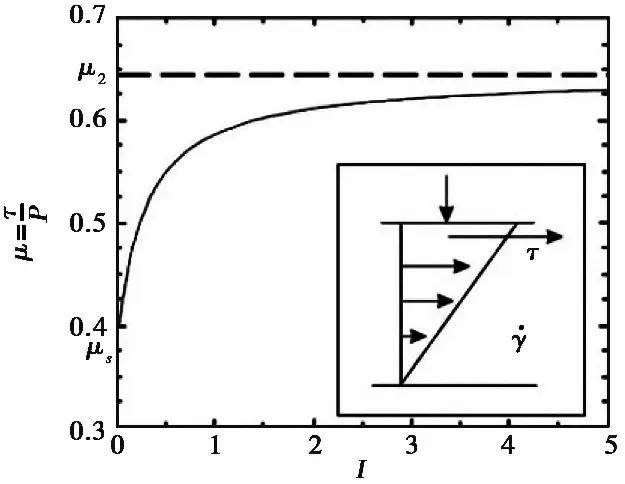
图4 摩擦系数μ和无量纲参数I的函数关系(Jop et al.,2006)Fig.4 Friction coefficient μ as a function of the dimensionless parameter I(Jop et al.,2006)
μ(I)=μs+(μ2-μs)/(I0/I+1)
(4)
式中:I0是一个常数;μs摩擦系数临界值;μ2摩擦系数极限值。
这种对颗粒流的简单描述已经可以实现对二维倾斜平面流和堆积流的流动速度预测,但却难以描述更复杂的密集颗粒流变特性,比如三维流变。因此,Jop et al.(2006)通过假设颗粒流动过程中致密区域中观察到的体积分数的微小变化可忽略不计,将颗粒材料描述为不可压缩流体,提出了三维颗粒材料流动模型:
σij=-Pδij+τij
(5)
(6)
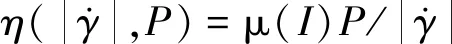
(7)
(8)
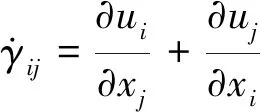
2.3 非局域流变
颗粒物质局域流变理论是从颗粒物质剪切速率出发的(Pouliquen et al.,2009),而当颗粒材料的剪切接近准静态时,颗粒物质局域流变便难以描述流动特性,会出现颗粒物质的非局域流变。非局域效应与局域流变所存在的偏差,通常会出现在如下两种情况(Koval et al.,2009;Kamrin,2012):在斜面流动中,颗粒流动层较薄时需要较大的倾斜角才能触发颗粒流动。因为在此时剪切应力与法向应力的比值(μ)是不变的,而静态屈服系数(μs)是与厚度有关的函数(Silbert et al.,2003);在大体积非均匀变形的颗粒材料中,局域流变预测在μ<μs区域不发生流动,但在μ<μs亚屈服区域实际存在极为缓慢颗粒流动,其剪切速率剖面具有指数衰减的特征,衰减长度与颗粒直径有关(Mueth,2003;MiDi,2004)。因此,局部流变在描述此类问题时存在着明显的局限性。
Kamrin et al.(2012)提出并验证了一种偏微分方程(PDE)非局域流动规律,旨在描述颗粒物质的稳态流动非局域性,通过颗粒材料的剪切速率和摩擦系数定义颗粒流体:
(9)
基于塑性重新排列会引起应力再分布的概念,定量描述ξ作为应力状态的函数。
(10)
通过拉普拉斯算子可以将非局域定律推广到二维空间上。因此,
2i
(11)
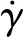
颗粒介质沿粗糙斜面向下流动,表现出许多非局域现象。Tang et al.(2018)研究了环形剪切试验中密集颗粒流的非局域流变,验证了非局域模型在描述流动特性方面的有效性。颗粒材料的密度变化的一个重要的特点是剪胀性,或由剪切变形引起的体积变形。Dsouza et al.(2020)提出了可考虑颗粒材料剪胀效应的缓慢颗粒流非局域流变模型,并分别在有无重力的情况下测试了此模型,发现它的预测与颗粒动力学模拟有很好的一致性。
颗粒物质力学领域内对于不同相态的颗粒系统研究均取得了一定的成果,如颗粒物质的剪切相变、颗粒物质局部流变和非局部流变等,但如何将不同相态的颗粒系统进行关联,建立统一的力学行为表征和不同尺度间的耦合关联,揭示颗粒物质跨尺度的物理机制,仍是目前颗粒物质剪切流动研究的重要内容之一。
3 典型颗粒物质力学实验方法
随着高精度、高采集频率的图像采集技术和高性能计算的诞生,传统的颗粒物质力学实验方法也得到了很大的改进。颗粒物质受力内部应力传递特征、力链网络结构可以通过颗粒材料的光弹实验直观地展现出来,颗粒材料内部的颗粒间局部位置发生非仿射位移可以通过颗粒物质的声发射和CT成像技术进行实时捕捉。与此对应各颗粒位移特征也可以通过粒子图像测速(PIV)、粒子跟踪测速(PTV)等计算方法实现在时间尺度的追踪。
3.1 颗粒材料光弹实验
光弹实验是应用光学原理研究弹性力学问题的一种实验应力分析方法。将具有双折射效应的透明塑料制成的结构模型置于偏振光场,给模型施加载荷时,可通过测量模型上产生的不同干涉条纹来确定其应力分布特征。以美国杜克大学Behringer教授为代表的科研团队,基于光弹测试方法在颗粒物质力学研究领域进行了广泛而深入的探索。颗粒材料光弹实验可以实现定量且无扰动的测量颗粒尺度上各颗粒的受力状态、细观尺度上的力链结构等重要参量(Zadeh et al.,2019)。
光弹性实验中最基本的就是平面偏振光装置,由光源和一对偏振镜组成,近光源的为起偏镜,远光源的为检偏镜(图5)。当两个偏振镜轴正交时形成暗场,互相平行时则为亮场。与线偏振光相比,使用圆偏振光可以得到更精确的各向同性测量结果。利用线性偏振器和四分之一波相移板组合的圆偏振器,可以将非偏振光转换为圆偏振光。如果材料没有受力,就没有透射光,就会产生暗像。然而,在材料中任何存在各向异性应力的地方,沿局部应力张量的两个主轴极化的波分量将以不同的速度传播。这种速度差异导致这两个波的组成部分的相对相移,在被测量物体表面就会形成明暗条纹,根据明暗条纹的分布形态便可以定量地计算出单个颗粒内部的应力场分布,以及颗粒与邻近颗粒间的接触力(Majmudar et al.,2005)。
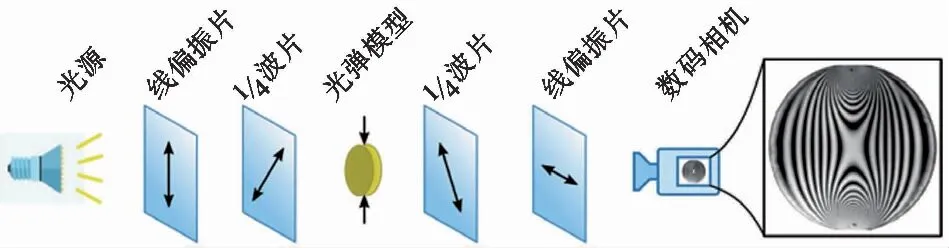
图5 暗场透射偏光镜的光弹性技术原理示意图(Zadeh et al.2019)Fig.5 Schematic image of the photoelastic technique for a darkfield transmission polariscope(Zadeh et al.2019)
颗粒材料光弹实验是研究二维颗粒材料受力后内部应力分布的重要实验方法。实验过程中通常将颗粒置于水平透明桌面上开展不同工况的实验研究,这样便不可避免地会受到颗粒与桌面间摩擦力对试验结果的影响,Zheng et al.(2014)通过开展密度匹配的试验方法消除底部摩擦力的影响,对比有无底部摩擦力试验结果后发现,颗粒底部摩擦力会在一定程度上改变剪切阻塞的临界体积分数,但不会改变剪切阻塞的基本现象。
3.2 颗粒材料声发射试验
声发射(Acoustic Emission,简称 AE)是指材料在受到应力作用或发生变形时,由于能量的快速释放而产生的瞬态弹性波(ASTM,2015)。对于颗粒材料而言,其内部颗粒的滑动和滚动摩擦、颗粒碰撞、颗粒破碎等一系列变形和运动机制都会产生声发射信号(Smith et al.,2019)。声发射监测技术通过压电传感器将颗粒材料所释放的弹性波转换为电信号,进而通过信号分析技术建立声发射信号参数与颗粒材料宏微观力学特性之间的关联(Chen et al.,2019)。
虽然声发射测试技术早期主要应用于金属、混凝土和复合材料等连续介质,近年来围绕颗粒系统的声发射特征已有较多进展,包括工程地质、岩土工程、采矿工程等不同学科领域(Johnson et al.,2008;Mojtaba et al.,2017;Dixon et al.,2018)。目前在工程地质领域,声发射监测技术已被广泛应用于典型颗粒系统如砂土地基的承载特性监测(Mao et al.,2015a,2018b)、土质边坡稳定性监测(Smith et al.,2015;Dixon et al.,2018)、颗粒破碎现象(Mao et al.,2015b;Mao et al.,2020)等领域的研究。大量现场监测以及室内试验研究结果表明,声发射特征与颗粒材料的屈服强度、峰值强度以及残余强度等力学特性有着密切的相关性(Mao et al.,2016,2018a;Smith et al.,2019;Lin et al.,2020;Smith et al.,2020)。此外,通过设置传感器阵列,可对声发射信号源进行三维定位,结合信号特征参数分析,进一步实现对颗粒材料内部力学状态演化的精细化分析。Mao et al.(2020b)通过声发射三维定位对桩底砂土颗粒破碎带的空间分布演化进行了分析。在此基础上,Lin et al.(2020)进一步对三轴加载条件下砂土试样的应变局部化过程进行了精细化分析。
3.3 颗粒材料CT成像技术
颗粒物质力学研究的一个重要方面是阐明颗粒体系的宏观力学行为与其内部微观结构演化之间的复杂关联(Jaeger et al.,1996)。然而,由于大多数颗粒材料是不透明的,在三维空间中研究颗粒体系内部的结构演化极具挑战。CT技术利用X射线对颗粒材料试样进行无损扫描成像,并通过图像处理技术进一步实现颗粒系统的三维重构,可实现颗粒体系内部结构的高精度定量化表征,已日益成为颗粒材料微观尺度研究的有力工具。
Kou et al.(2017)借助CT扫描成像技术对准静态循环剪切三位颗粒系统的微观动力学进行了深入的研究,证实了颗粒的微尺度弛豫动力学遵循一个振荡剪切的规律,发现颗粒的分布和位移可由Gumbel定律描述,导致一般意义上认为的颗粒固体,其实是一种处在液固边界的临界相,在外部微扰下就会流动,更类似于复杂流体。Li et al.(2014)利用快速X射线层析成像技术对无热颗粒堆积过程进行监测,发现当填料是湿的且存在短程吸引作用时,颗粒体系存在具有五重对称性的局部优先结构,与胶体凝胶具有很大的结构相似性。Cheng et al.(2018)通过小型三轴原位X射线扫描装置对颗粒材料(球形玻璃珠和角状玻璃珠)剪切过程的颗粒间接触演化进行了研究,获取了剪切全过程的应力-应变响应、颗粒位移演化、配位数和接触运动特征等。Athanassiadis et al.(2014)利用X射线断层扫描系统,研究颗粒材料在机械载荷下的响应,并讨论了三维计算机断层扫描系统的标定,以及图像重建过程。Chevaller et al.(2019)使用微聚焦型X射线计算机断层扫描(CT)与直剪试验装置研究了砂土作为刚性颗粒和轮胎切屑作为弹性颗粒在直剪条件下的力学行为。Laurent et al.(2020)利用X射线断层扫描技术研究了高粱和水稻在漏斗流动过程中堆积密度、配位数和颗粒旋转的变化。
3.4 颗粒运动测量
随着光学技术的发展,出现了许多新的光学非接触测量方法。基于数字图像的颗粒流速测量方法主要有:粒子图像测速(particle image velocimetry,PIV)、粒子跟踪测速(particle tracking velocimetry,PTV)以及空间滤波测速法(spatial filtering velocimetry,SFV),其中粒子跟踪测速和粒子图像测速在颗粒流实验测量中应用最为广泛(杨晖等,2018)。然而,如果颗粒流浓度较高,PIV在识别颗粒位移的能力方面远远落后于PTV(Fu et al.,2018)。同时,如果颗粒流流速对比较大,SFV法由于测量结果平均,可能会造成较大的测量误差。通常,PTV是测量复杂颗粒流的最佳方法(Wang et al.,2019a)。
Dai et al.(2020)采用粒子图像测速(PIV)技术,测量了玻璃珠、刚玉珠和粗砂3种典型颗粒材料的静止角、内摩擦角、颗粒壁面摩擦角以及流动特性。Zhang et al.(2020)研究了地面和水下颗粒柱崩塌过程中的能量演化规律。Alsaydalani(2020)采用粒子图像测速技术(PIV)研究了水平水射流作用下颗粒床的破坏机理。Huang et al.(2020)采用粒子图像测速技术,研究了颗粒桩重力崩塌诱发冲击波的过程。Sudeshna et al.(2019)研究了粗糙和光滑表面的干燥玻璃珠剪切带性质以及剪切单元填充高度和旋转频率的依赖关系。
可以看到,颗粒物质力学实验的基本思路是综合运用光、声、振动、射线等各种测试手段,获取单个颗粒(或颗粒集合)的实时空间位置、颗粒形态和受力状态等参数,以此来分析整个颗粒系统的力学行为。测试结果通常较为精确,直观,可为揭示颗粒系统的力学状态提供必要的基础数据。但各种测试方法都存在一定不足,如光弹、PIV技术主要适用于二维平面颗粒,CT技术主要用于小型单元试样。由于颗粒系统的特点,测试精度与研究尺度之间永远是一对矛盾。如何发展适用于颗粒系统大尺度、三维的测试方法,是颗粒物质实验领域的一个重要研究方向。
4 工程地质中颗粒物质力学问题
颗粒物质是工程地质体的主要物质形态之一(Zheng et al.,2019a)。自然界中常见地质体的灾变过程,如边坡失稳破坏、泥石流和海底滑坡等都与颗粒物质力学息息相关。地质体的灾变是从稳定态到非稳定失稳变形、继而发生大变形流动的复杂演变过程。从颗粒物质力学角度上看,是组成地质体的颗粒集合体在外部边界的约束下,由阻塞状态发展为流变状态的过程。因此,深化颗粒物质力学理论在工程地质灾害中的应用,对进一步理解工程地质灾害的致灾机理具有重要意义。
4.1 松散地质体稳定性研究
局部塑性变形涉及颗粒在几个颗粒间距离的小区域内的协同重排、非仿射位移、自组织成剪切带等,最终导致材料发生破坏(Zheng et al.,2018a)。理解非晶态固体的结构和动力学之间的联系在物理学、岩土工程以及地球物理学等领域是必不可少的(Wang et al.,2020)。
松散地质体形成剪切带演化至失稳破坏现象的本质其实是细观尺度上的颗粒力链断裂与重建、各颗粒空间位置发生非仿射位移后重新排布(郑虎,2014)。颗粒物质领域内的光弹实验对揭示颗粒系统内部细观尺度力链结构分布特征有着极大的优势,对从力链尺度揭示松散地质体剪切带演化、失稳的研究有重要的应用前景。Zheng et al.(2019a)利用光弹性测试技术进行颗粒物质的双轴实验,研究了光弹性颗粒体系中剪切带力链网络的发展过程(图6)。除此之外,通过对颗粒系统中各颗粒的空间方位进行追踪。定量揭示了颗粒材料在剪切过程中,随着剪切带的演化,局部体积分数、力链网络分布特征、各颗粒的转动量等微/细观参量的变化特征。并指出在剪切带区域内,位移场与旋转场有很强的相关性。颗粒物质的阻塞相变理论对松散地质体的稳定性研究也具有重要的指导意义,Zhao et al.(2019)通过开展均匀剪应变场的颗粒材料Couette剪切试验研究,观察到在大剪切应变下小于临界体积分数范围内会使得颗粒体积达到稳定性的临界状态。

图6 不同剪应变下颗粒材料内部的力链网络(Zheng et al.,2019a)Fig.6 The snapshots of the force chain network at different strains(Zheng et al.,2019a)
在颗粒物质力学的研究中,由于颗粒系统所展现出来的复杂性,通常会采用由二维圆盘或三维球组成的颗粒系统为研究对象,在认识许多颗粒物质力学行为的物质机制方面取得了很多创新性研究成果。然而,对非球形粒子系统,即椭圆、多边形无论是试验还是数值模拟的开展都有一定的难度,但近年来均已得到了较好的解决。对于颗粒材料光弹实验而言,由于制作圆盘颗粒相对容易,绝大多数的研究成果是通过对二维圆盘的总结得出的。近年来,由于浇筑法制作光弹颗粒方法的发明,并结合3D打印技术,使得通过光弹实验研究其他形状的颗粒材料成为了可能。Wang et al.(2020)研究了简单剪切作用下由椭圆组成的准二维颗粒系统。通过跟踪椭圆的位置和方向,发现随着剪切应变的增加,椭圆逐渐旋转并沿优选方向排列。同时,椭圆系统的剪切阻塞,系统压力和配位数随剪切应变增加。
4.2 岩土颗粒物质大变形流滑
在山区,松散岩土体在重力驱动下极易发生失稳破坏并进一步演化为大变形流动,造成岩石崩塌、滑坡和泥石流等地质灾害事件(Campbell et al.,1995)。高速远程滑坡和泥石流是工程地质灾害中典型的颗粒物质大变形问题,具有运动速度高、滑动距离长、破坏力大的特点,往往造成重大经济损失和人员伤亡(Dowling et al.,2014)。
1932年,Heim发表了关于瑞士埃尔姆的高速远程滑坡的系统研究成果,揭开了世界范围内研究学者对高速远程滑坡开展深入研究的序幕。多年来,众多地质和工程学家,对欧洲阿尔卑斯山区、加拿大落基山区、美国加利福尼亚山区和日本等山区发生的高速远程滑坡事件进行了调查和分析(程谦恭等,2007)。2008年汶川大地震触发了大量的高速远程山体滑坡,造成了巨大的经济损失和人员伤亡(殷跃平,2008)。2015年深圳市发生山体滑坡,造成管道受损泄露并发生爆炸,造成73人死亡。因此,大型山体稳定性和高速远程滑坡问题,已成为山区大型基建必须考虑的重要研究课题。
除了高速远程效应外,高速远程滑坡一般还具有以下4个基本特征:流态化、尺寸效应、层序保持现象、反序现象(程谦恭等,2007;张明等,2010)。汪发武(2019)通过环剪试验以及对滑坡现场调查分析,探讨了地震诱发滑坡土结构和土粒子破碎产生的滑动带液化的不同机理,论述了两种机理对滑坡灾害预测研究中的重要性。黄润秋等(2008)对汶川地震后大光包巨型滑坡的基本特征及形成机理进行了分析,发现斜坡的临空条件和贯通性好的岩层面是滑坡产生的基础,长持时和高强度地震是导致滑坡的根本因素,并把滑坡产生的机理和过程分为坡体震裂、松弛和解体阶段。殷跃平(2008)对汶川地震触发的高速远程特征进行了分析,滑坡主要沿龙门山中央断裂带地震破裂带展布,并具有以下特征:母岩强烈风化破碎、抛掷效应、碰撞效应、铲刮效应和气垫效应。刘广煜等(2019)基于块体离散元方法,以易贡滑坡为例研究了高速远程滑坡的灾害动力机制。葛云峰等(2019)基于室内物理模型试验,通过PIV技术获取滑体颗粒的水平速度、竖直速度、位移等运动参数,研究了高速远程滑坡堆积过程中的能量传递机制。Huang et al.(2012)采用SPH方法(光滑流体动力学)模拟强震触发的滑坡,通过在SPH中引入宾汉姆流体模型,能较好模拟滑坡体的变形流动过程。Zhu et al.(2020)用分子动力学软件Lammps模拟了振动作用下倾斜表面上的颗粒流动,探讨地震动效应对山体滑坡运动特征的影响机制。目前,单相颗粒流流变理论发展相对成熟。但是,面对复杂海洋环境条件下的海底滑坡诱发过程,基于流变学理论的多相流模型的建立仍然是一个挑战。
泥石流也是世界各地山区常见的灾害。我国山区极端暴雨型泥石流经常发生,在2008年汶川地震后20万个山体滑坡被触发,野外调查表明,许多滑坡堆积物由于降雨被重新搬运,并导致随后的浅层滑坡和泥石流(Xu et al.,2014)。类似的还有中国台湾Chi-Chi地震后的斜坡堆积物在台风季节的强降雨作用下被侵蚀搬运,造成了灾难性的泥石流灾害(Shieh et al.,2009)。因此,加强泥石流的孕育、运动致灾机理研究是地质灾害防灾减灾领域的重要课题。泥石流是以重力为主要驱动力的固液两相混合流体,固体颗粒物质含量高,粒径相差大,具有典型的非牛顿流体特征。泥石流颗粒之间的接触力链演化规律可以基于颗粒物质力学理论和方法进行分析。Iverson et al.(2014)结合了临界状态土力学、颗粒流动力学和流体力学推导了一个深度平均的两相模型,模拟泥石流从起始到沉积的流动行为。模型的平衡方程描述了固体体积分数、基底孔隙流体压力、流动厚度和流速两个分量的耦合演化。颗粒流模型更适用描述含有粗颗粒的泥石流运动,符合泥石流的动力特征,在泥石流数值模型理论研究中取得了大量研究成果。
总体上看,岩土颗粒物质的大变形流滑问题,本质上都涉及颗粒物质力学中的相态转化和流变问题。颗粒物质力学发展至今,已经为合理描述颗粒系统的力学行为提供了较为完备的理论基础,颗粒物质力学理论和方法的引入可为解决工程地质领域的颗粒物质问题提供更广阔的空间。但需要指出的是,基于物理学发展而来的颗粒物质力学,其主要应用性成果如颗粒阻塞相变图、流变模型等,虽然具有一定的普适性,但本质上对颗粒材料本身特征、边界条件和所处力学状态等都具有一定依存性。面对工程地质领域的颗粒物质问题,如何基于其独特的颗粒材料特征及力学条件,合理引入颗粒物质力学理论和方法,是成功解决工程地质灾害问题关键,仍需要大量的实验验证及理论分析的支持。
5 结论与展望
松散地质体属于颗粒物质范畴,表现出了极为复杂的力学性质,许多由松散地质体变形破坏所致地质灾害的本质即为颗粒物质阻塞至未阻塞间的相态转化,与之对应的便是松散地质体的力学稳定态到力学非稳定态间的转变。颗粒物质力学中相关的理论方法可以为松散地质体变形破坏致灾的研究提供新的思路。例如,颗粒通过颗粒材料阻塞相变性质揭示土石混合体的力学行为随土与石的比例不同而发生的非连续突变等。
许多颗粒物质力学研究的常用实验方法也可以借鉴到工程地质领域内,如光弹实验方法、声发射等。光弹实验方法对实验对象有所要求,必须采用具有人工双折射性质的材料,虽然有别于传统的岩土体材料,但揭示的颗粒材料基本力学特性在工程地质领域也是具有普适性的。当然,颗粒光弹试验也具有其局限性,虽然可以针对不同形状的颗粒系统开展相关研究,但目前还难以拓展到三维的颗粒系统,需要结合折射率匹配、大量的图像处理等技术;声发射试验方法所监测的弹性波信号可直接反映其发生源的物理力学机制,大量涉及地质体变形破坏的工程地质问题,如滑坡失稳、碎屑流长距离运动、地震孕育等,都可通过其伴生的声发射信号进行反演分析。声发射信号的关键参数特征提取及其与信号源物理力学机制的关联性研究目前仍具有广阔的发展空间。
物理领域内所研究的颗粒物质力学通常是从较为简单的物理模型或数值模型得到的,如何将相关的研究成果应用到复杂的工程地质领域中,是成功交叉融合颗粒物质力学和工程地质学的关键。特别是颗粒物质相变的研究成果多基于双分散圆形或球形的规则形状颗粒体系,工程地质领域所遇到的颗粒物质力学问题往往是不规则形状,且分选性也非常差,虽然颗粒物质的相变是客观物质规律,但复杂岩土颗粒材料的临界体积分数却难以确定。除此之外,针对黏性颗粒材料的颗粒物质力学研究,目前虽有一些数值模拟的研究成果,但在试验上难以定量地控制颗粒间的黏聚力,黏性颗粒物质力学试验研究仍处于探索阶段。

