电网卫星授时系统中基于定向天线的北斗干扰源定位

陈 斌，陈真通，章坚武，王旭旭，章坚民

（1.浙江双成电气有限公司，浙江 绍兴 312000；2.杭州晨晓科技股份有限公司，杭州 310018；3.杭州电子科技大学 a.通信工程学院；b.自动化学院，杭州 310018）

0 引言

电网是一个巨大的系统工程，要确保电厂、变电站的设备运转同步进行，必须首先要确保设备内部时钟的一致性，一般电力系统要求授时系统的内部时间精度要达到百纳秒级[1-3]。为了统一内部时钟，我国电力系统开始采用北斗卫星信号作为主要的授时手段，通过北斗的民用频道向电力系统的电力自动化设备、微机监控系统、安全自动保护设备、故障及事件记录等智能设备提供授时信号，以实现电力系统的同步运行[4-6]。一旦电力系统如智能变电站的卫星授时系统受到欺骗攻击，授时数据可能被篡改，严重威胁到电力系统的安全稳定，甚至导致同步电力系统瓦解和崩溃。

北斗系统[7]起步较晚，但近些年来发展迅猛。目前，正在运行的北斗二号系统播发B1I 和B2I公开服务信号，免费向亚太地区提供公开服务。服务区为南北纬55°、东经55°～180°区域，定位精度优于10 m，测速精度优于0.2 m/s，授时精度优于50 ns[8]。北斗系统的单向授时精度和双向授时指标均优于国外同类系统。但是由于北斗信号民用部分的导航电文格式、编码调制方式、载波频率等信息都是公开的，很容易受到欺骗干扰。

当前通用的欺骗干扰主要包括对真实卫星导航信号直接转发[9]和模拟信号源直接产生欺骗信号这两种模式[10-11]。对于处于捕获阶段的接收机，这两种欺骗干扰方式均可通过其功率优势引导目标接收机对其进行捕获跟踪。目前公开的文献在涉及欺骗成功牵引条件时均只定性地说明需要较高的欺骗功率。国防科技大学卫星导航研发中心黄龙等[10]通过对接收机伪码跟踪环路稳定点的理论分析，得出了对已经跟踪上真实卫星信号的导航接收机实施有效欺骗的信号功率条件，并通过软件接收机仿真和实际设备实验两种方式验证了理论分析的正确性。文献[11]通过实验定量验证了实施有效欺骗干扰需要较高的欺骗功率。

除了通过功率检测判断北斗接收模块是否受到了欺骗干扰外，文献[12]提出了两种分布式检测北斗欺骗干扰的方法。基于信噪比的检测方法提取接收模块解析的信噪比特征，将两个接收模块解析同一卫星信号信噪比之差的方差与判决阈值比较，从而判断北斗接收机是否受到欺骗干扰；基于相对距离的检测方法提取接收模块解析的位置特征，将两点定位位置的距离与实际物理距离进行比较，从而判断北斗接收模块是否受到了欺骗干扰。最后通过实验验证了两种分布式北斗欺骗干扰检测方法的有效性。

电网中的北斗接收模块检测出受到欺骗干扰后，需要快速准确确定干扰源的方向和位置，查明原因予以排除，以保证电网的安全运行。文献[13]利用阵列天线，通过RELAX 算法比较各个方向上功率比的大小来判断DOA（到达波方向），并通过矩阵正交运算来抑制干扰源方向的信号。这种方法对阵列天线的方向敏感性要求比较高，而且需要预先设定检测卫星信号的个数，如果干扰源模拟发射的伪卫星信号的数量比较多，该算法就会出现检测误差。

本文提出一种定位北斗干扰源的办法。根据定向天线方向辐射图的对称性，采用测量信噪比峰值下降点的办法测量出北斗欺骗干扰源的方向，在不同地点得到多组测量数据之后，使用最小二乘法逐渐逼近干扰源的真实位置。本文还提出一种根据测向误差估算干扰源位置范围的方法，将最小二乘法的更新初值设置在此范围内，可以保证算法逼近干扰源位置。

1 八木定向天线测向方案

图1 所示的欺骗干扰检测示意图是单北斗干扰源的情况，图中1 和2 分别表示北斗接收机1和2。

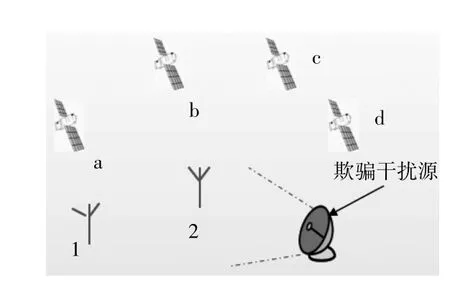
图1 分布式欺骗干扰检测

实验中采用北斗频段的八木定向天线。图2是一种八木定向天线在1.55 GHz 的辐射方向图，可以看出，该定向天线的辐射方向图具有对称性，其波束角为24°。

北斗接收机的分析数据以NMEA（GPS 导航设备统一的RTCM 标准协议）串口传输到计算机，可以通过NMEA 中的信噪比判断北斗信号的功率强度。具体的测向流程如图3 所示。

第一步，连接定向天线、接收机、计算机，并保证定向天线水平放置。

第二步，顺时针旋转定向天线，并从计算机的串口助手读取该方向各个北斗信号的信噪比。找到北斗信号信噪比最大的天线角度的范围θa～θb。

图2 八木定向天线在1.55 GHz 的辐射方向图

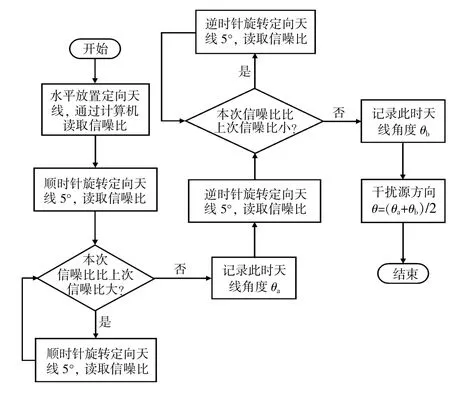
图3 利用定向天线测向流程

第三步，求出干扰源方向为：

由于定向天线的波束角，以及接收机分析到信噪比数据的离散性，定向天线在一定的角度变化时，信噪比的最大值是不变的。采用式（1），即使定向天线的波束角比较大，由于定向天线辐射方向图的对称性，也能减小测向误差。

2 最小二乘法估计北斗干扰源位置

利用定向天线测向的办法，可以在位置（x1，y1）处估计干扰源的方向θ1。图4 表示在4 个不同位置测量干扰源的方向，其中位置1—4 的坐标为已知量，定向天线测量的方向角为测量量。

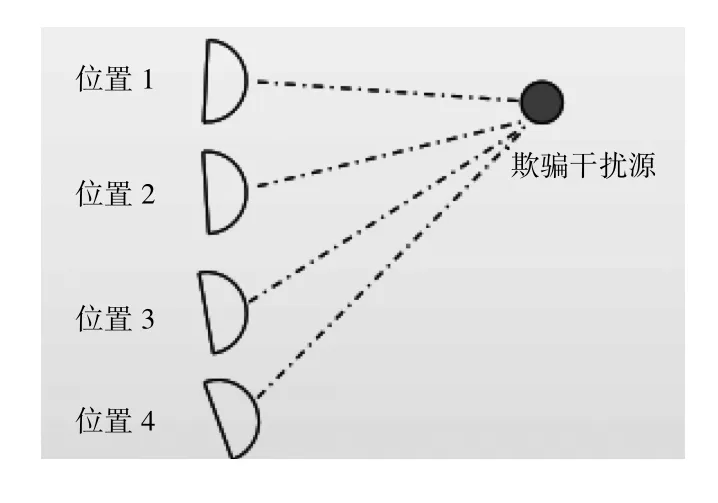
图4 在4 个不同的地点测量干扰源方向

2.1 最小二乘法估计北斗干扰源算法

本文采用最小二乘法估计北斗干扰源的真实位置（x，y）。首先利用定向天线测向的办法，可以在位置（x1，y1）处估计干扰源的方向θ1。为了减小估计误差，可以在4 个或者4 个以上的地点，分别测量干扰源的方向，然后得到：

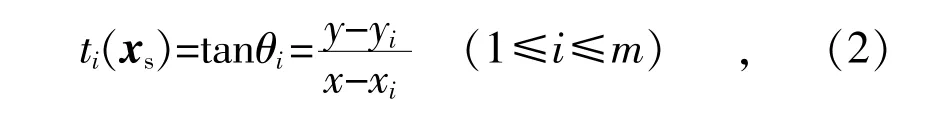
式中：i 表示第i 次测量，i=1，2，…，m，m 为总测量次数；（xi，yi）为第i 次测量的地点；θi为第i次测量的干扰源方向；ti（xs）为第i 次测量干扰源（x，y）方向的正切值。

假设北斗干扰源的估计位置值为（x0，y0），将（x0，y0）带入式（2）可以求出ti（xs）的初始值ti（x0），这里xs指欺骗干扰方向，x0为初始估计干扰方向：

对式（2）求偏微分可以得到：

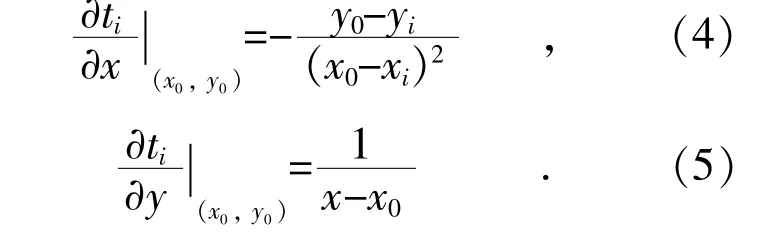
为了使用最小二乘法，利用泰勒展开将式（2）线性化，并引用式（3）—（5）的结果，可以得到：

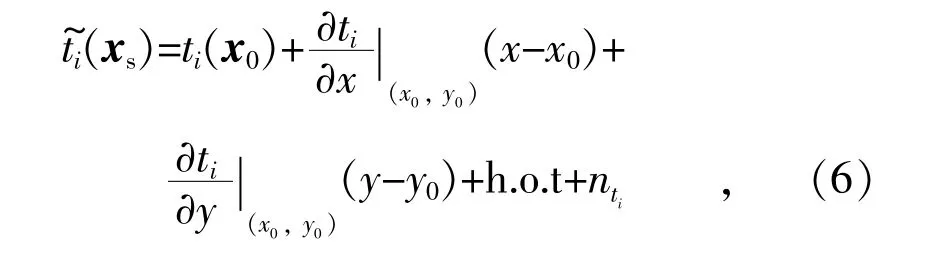
式中：h.o.t 是高阶泰勒级数项；nti为测量噪声；（xs）为观测干扰源方向正切值。

为了用矩阵的形式表示多组测量数据的运算，可以定义矢量ui，dx0：

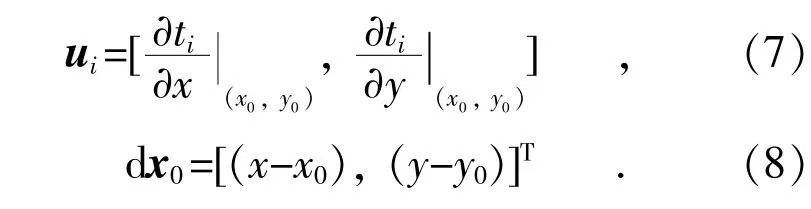
将ui，dx0带入式（3）得到：

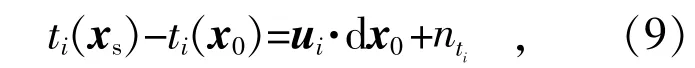
将式（9）的左边写成δti，然后定义：

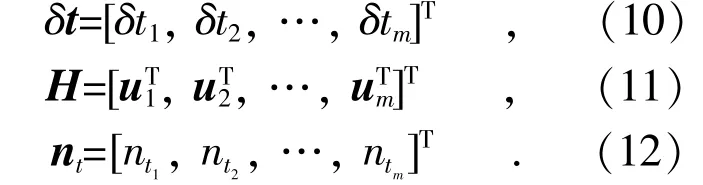
这3 个矩阵的维数分别为m×1，m×2 和m×1。δt 表示m×1 测量正切值与实际正切值的差值，H 与更新值（x0，y0）及式（2）的偏微分有关。当存在多组测量数据时，可以将式（10）扩展为：

根据最小二乘法，利用观测值∂t，可以得到dx0的估计值：

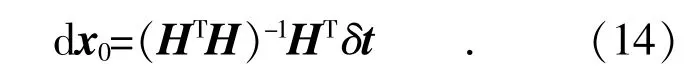
式（14）得到的值是通过一次线性化后初始值和真实值之间的修正量，将这个修正量用来更新初始点，得到修正后的解，即

然后再以x1作为起始点来重复从式（8）到式（15）的过程，得到新的修正量dx1来更正上一次的解。

上述过程用通用的方式来描述，对k 次更新来说，其过程为：

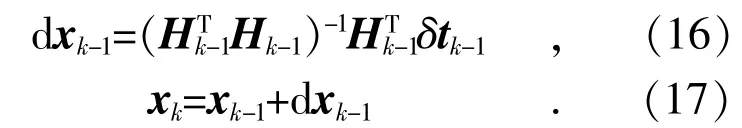
式（16）、式（17）中H 和δt 都加了下标，因为每一次更新xk以后都要重新计算H 和δt。

式中：T 为预设门限值。

当满足式（18）终止条件后，通过式（17）得到的xk-1为对干扰源二维位置（x，y）的估计值。

2.2 最小二乘法初值选取

在模拟最小二乘法的时候发现，设定不同的初值，有可能会更新到不同的极值点，或者更新不到极值点。为了保证最小二乘法更新到对干扰源位置的正确估计，需要将初值设定在估计干扰源的附近。本文利用2 组采样数据计算出更新初值点。

设定向天线在（x1，y1），（x2，y2）测得的干扰源方向分别为θ1，θ2，这2 个角度的正切值为t1，t2，根据式（3）可以得到：

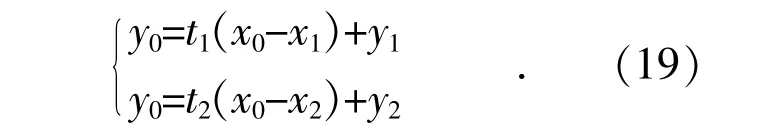
求解方程组（19）得到：

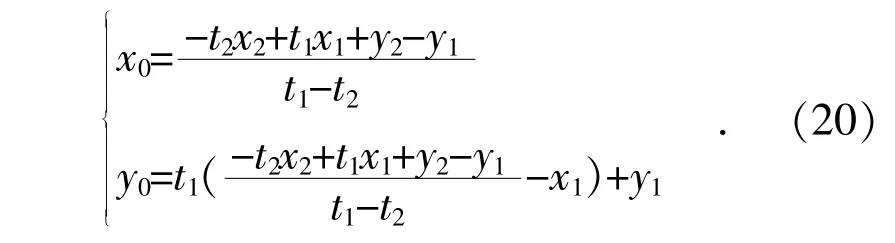
通过式（20）得到的（x0，y0）为利用2 组数据得到的对干扰源真实位置（x，y）的估计。由于仅仅利用2 组数据，估计值（x0，y0）与真实值（x，y）的偏差比较大。在最小二乘法中，如果x0与x，或者y0与y 比较接近，就可以根据式（16）、式（17）逐渐递归到比较准确的干扰源位置估计值。图5为干扰源测量位置与真实位置误差示意图。

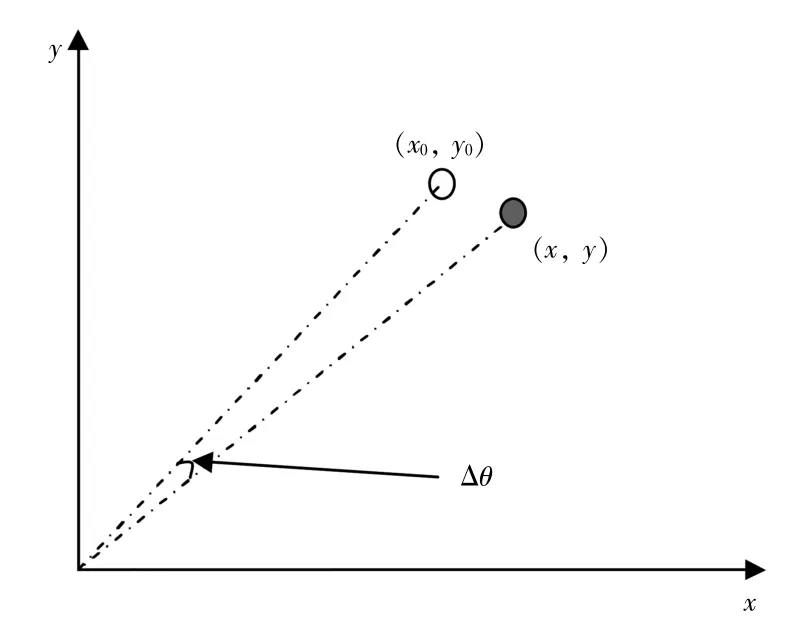
图5 干扰源测量位置与真实位置误差

如图5 所示，假设（x0，y0）与（x，y）的误差在±Δθ 之内，则可以根据Δθ 计算出x0的误差范围：

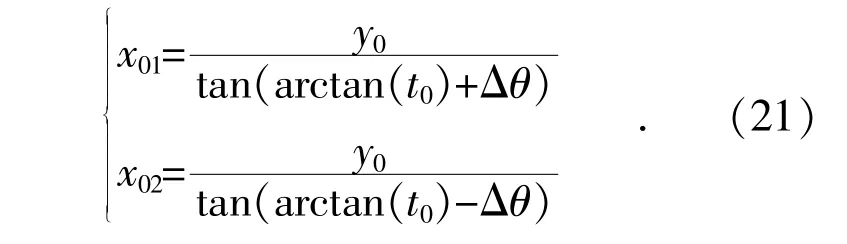
其中

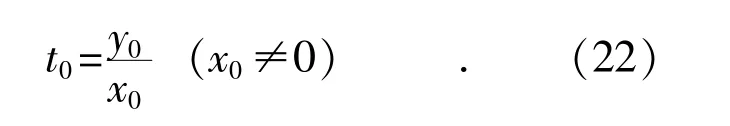
在x 的取值范围（x00，x01）中，存在接近x 的值，保持y0不变，x0遍历（x00，x01）中的值作为参考初始值。将这些参考初始值依次带入式（16）、式（17），如果结果逼近某个坐标，说明该坐标是对干扰源位置（x，y）的最佳估计，停止更新；否则，取另一组参考初始值进行逼近。

3 算法仿真

保证干扰源在测量点的1 000 m 之内，设定干扰源的位置坐标（单位m）为（600，900）。利用定向天线，在6 个不同地点测量干扰源的方向。根据式（16）、式（17），选取最小二乘法的更新初值，设置初值与干扰源真实位置的角度误差在10°之内。设置最小二乘法初值更新的阈值为0.01。从定向测向误差和测量点位置误差两个方面，观测该算法在测量参数存在误差的情况下对干扰源的定位效果。

3.1 测向误差对干扰源定位结果的影响

设定干扰源的位置为（600，900）。模拟定向天线在6 个不同地点的测向数据，测量点位置无误差，测向误差分别为5°和3°的测量数据见表1。

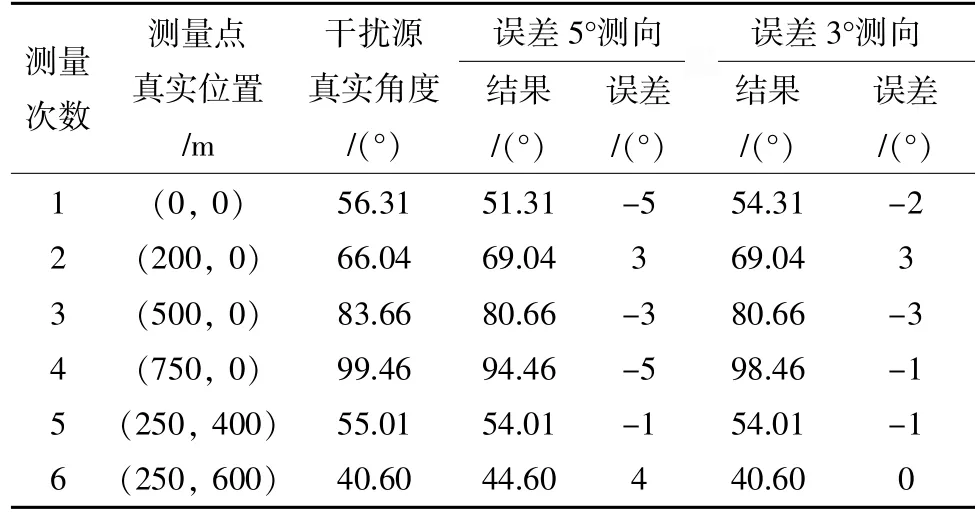
表1 测向误差在5°和3°时的测量数据

根据表1 中的数据，利用式（12）可以得到更新初值，利用式（21）可以得到初值范围，利用式（16）—（18）可以不断迭代，更新初值，最终得到表2 的逼近结果。

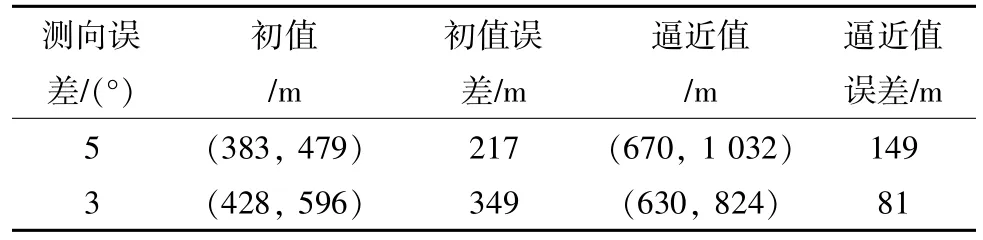
表2 测向误差在5°和3°时的定位结果

从表2 可以看出：用本文最小二乘法的定位误差（初值误差）比直接通过式（20）得到的定位误差要小；最小二乘法所采用的数据组比较多，而式（20）只利用2 组测量数据，所以式（20）对误差比较敏感；测向误差比较小时，利用最小二乘法得到的逼近结果与真实干扰源的位置误差也较小。

3.2 测量点位置误差对干扰源定位结果的影响

假设表1 中6 次测向数据无误差，测量点位置误差分别为10 m 和50 m，通过软件仿真可以得到表3 的测量数据。

表3 测量点位置误差在10 m 和50 m 时的测量数据

根据表3 中的数据，利用式（20）可以得到更新初值，利用式（21）可以得到初值范围，利用式（16）—（18）可以不断迭代，更新初值，最终得到表4 的逼近结果。

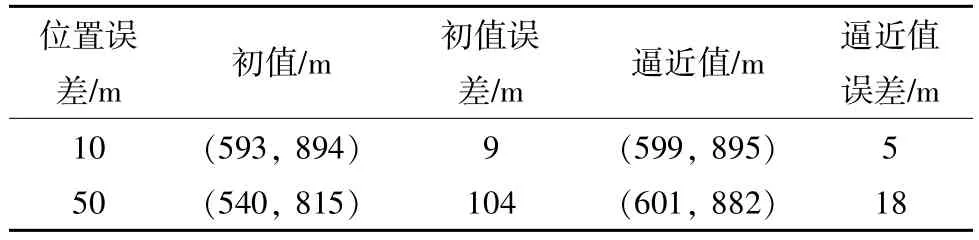
表4 测量点位置误差在10 m 和50 m 时的定位数据

从表4 可以看出：在对干扰源定位时，利用最小二乘法逼近的误差比直接通过式（20）计算干扰源的误差要小；测量点的位置误差越小，利用最小二乘法对干扰源位置逼近结果的误差越小。

3.3 测向误差与测量点位置误差的比较

测向误差的来源包括定向天线的精度、定向天线波束角的大小、信噪比计算误差、测向角度读取时的误差。测向误差与定向天线的波束角有密切关系，提高测向精度首先要减小定向天线波束角角度，波束角越小，测向精度越大。但是，减小波束角会增大定向天线的体积，从而提高定向天线的制作成本。因此，需要综合考虑定向天线测向精度和定向天线的制作成本来选择定向天线的波束角。

测量点位置误差来源于测量用尺的精度以及尺子长度的读取，一般而言，测量长度越长，测量点的位置误差越大。

比较表2 和表4 可以发现，测向误差比测量点位置误差更容易对测量结果造成影响。当测向误差为5°时，干扰源定位误差为149 m；当测量点位置误差为50 m 时，干扰源定位误差仅为18 m。所以，本文算法对测量点位置测量要求不是很高，对测向精度要求较高。

4 结语

本文分析了电力系统中时间同步的重要性，介绍了三种发现北斗接收机受到欺骗干扰的方法，提出了一种定位北斗干扰源的方法。该方法根据定向天线方向辐射图的对称性，采用测量信噪比峰值下降点的办法测量出北斗欺骗干扰源的方向，在不同地点得到多组测量数据之后，使用最小二乘法逐渐逼近干扰源的真实位置。本文还提出了一种根据测向误差估算干扰源位置范围的方法，将最小二乘法的更新初值设置在此范围内，可以保证算法逼近干扰源位置。通过软件仿真了在1 000 m 之内定位北斗欺骗干扰源的效果，结果表明定向天线的测向精度为±5°时，仍然可以较为准确地定位干扰源。

当前对卫星接收机的欺骗干扰主要包括自发式欺骗干扰和转发式欺骗干扰，而这两种欺骗干扰方式产生的伪卫星信号功率都要比真实信号的功率高。接收机在接收欺骗干扰前后所处环境的噪声变化基本相同，因此信噪比的变化主要体现在信号功率的变化。本文提出的方法采用信噪比可以检测出伪卫星信号源的方向，同时适用于转发式欺骗干扰源和自发式欺骗干扰源定位。

本文目前只考虑单一欺骗干扰源的情况，在今后的工作中，需要考虑如何定位多个欺骗干扰源的情况。