挤压AZ31镁合金的动态力学行为及本构模型

李飞龙，肖 罡，郭鹏程，仪传明，刘晓红

(1.南南铝业股份有限公司，广西 南宁 530200；2. 江西应用科技学院 工程技术协同创新中心，江西 南昌 330100；3.湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082；4.九江职业技术学院 机械工程学院，江西 九江 332007)

镁合金作为目前最轻的金属结构材料，具有优良的阻尼性和切削加工性，是实现汽车、武器和航空航天装备轻量化的理想材料[1]。目前，镁合金已应用于座椅、变速器、轮毂、军用车身及桥壳、火箭弹、飞机尾翼和航空发动机框架等[1-5]。镁合金应用于汽车、武器和航空航天领域时不可避免地要承受高速冲击载荷[5-7]，这使得研究者越来越关注镁合金的动态力学行为。

近年来，已有较多关于镁合金在动态冲击载荷下的变形行为、组织演变和变形机制的报道[6]。郭鹏程和毛萍莉等[7-10]的研究表明，AM80和AM60B镁合金具有较强的应变速率效应，其塑性和形变吸能性均随应变速率的增加呈现不同程度的增加。徐伟芳等[11]则发现AZ31镁合金在高速冲击载荷下的屈服强度与应变速率无关。与准静态加载相比，AZ91C镁合金在冲击载荷下的应变硬化能力显著提高[12]。提高加载应变速率能够细化形变孪晶，使其变形机制由位错热激活转变为孪生和滑移相协调[13-14]。采用Johnson-Cook(J-C)力学本构能够较为准确地预测镁合金的动态力学行为[6, 15]，但当产生绝热剪切变形时，本构拟合精度降低。基于J-C本构，通过引入Arrhenius型本构等可大幅提高本构模型的拟合精度[7,16-17]。

本文作者基于高速冲击实验，开展挤压AZ31镁合金在880 s-1～4 820 s-1应变速率范围内的动态力学响应行为研究，并以0.001 5 s-1作为参考应变速率，建立可准确表征挤压AZ31镁合金动态力学响应的本构模型，为AZ31镁合金的工程应用提供实验支持。

1 实验材料与方法

本实验采用AZ31镁合金圆铸锭，其化学成分如表1所示。采用到温入炉的方式将直径为120 mm的商用AZ31镁合金圆铸锭放到400 ℃的箱式电阻炉中保温4 h；将铸锭挤压成直径为25 mm的圆棒材，挤压比为23；将挤压棒材放入预热至420 ℃的箱式电阻炉中固溶处理6 h后空冷，得到实验用的AZ31镁合金棒材。合金棒材的晶粒尺寸较均匀，平均晶粒尺寸约为46 μm，未见初始孪晶，如图1所示。

表1 AZ31镁合金的主要化学成分(质量分数/%)Table 1 Main chemical compositions of AZ31 Mg alloy(wt/%)

图1 AZ31镁合金棒材的金相组织Fig.1 Initial Optical image of the extruded AZ31 Mg alloy

采用火花放电线切割机沿棒材纵向切取压缩试样。高速冲击和准静态压缩的试样尺寸分别为Φ8 mm×4 mm和Φ8 mm×8 mm，试样与棒材的相对位置如图2所示。

图2 取样位置示意图Fig.2 Schematic diagram of sampling location

高速冲击和准静态压缩分别在分离式霍普金森压杆(Split Hopkinson pressure bar,SHPB)和INSTRON电液伺服实验机上进行，加载应变速率分别为0.001 5 s-1、880 s-1、1 410 s-1、3 430 s-1和4 820 s-1。为减少误差，相同应变速率下应力-应变数据均取3次有效实验的均值。压缩变形后，沿试样轴线切取金相试样，经机械抛光和腐蚀后(液腐液成分为：5 mL乙酸、6 g苦味酸、10 mL蒸馏水和100 mL乙醇)，在光学显微镜上进行金相组织观察。

2 应力响应行为

实验用AZ31镁合金的真应力-应变曲线如图3所示。由图3可知，合金的流变应力随应变速率的增加而增加，具有明显的正应变速率效应，且冲击载荷下的流变应力明显高于准静态的。这是由于随加载应变速率的增加，变形响应时间减小，需要诱发更多的孪生以协调各晶粒间的变形[7]，与滑移相比，孪生的临界应力要高，故合金表现出正的应变速率效应。

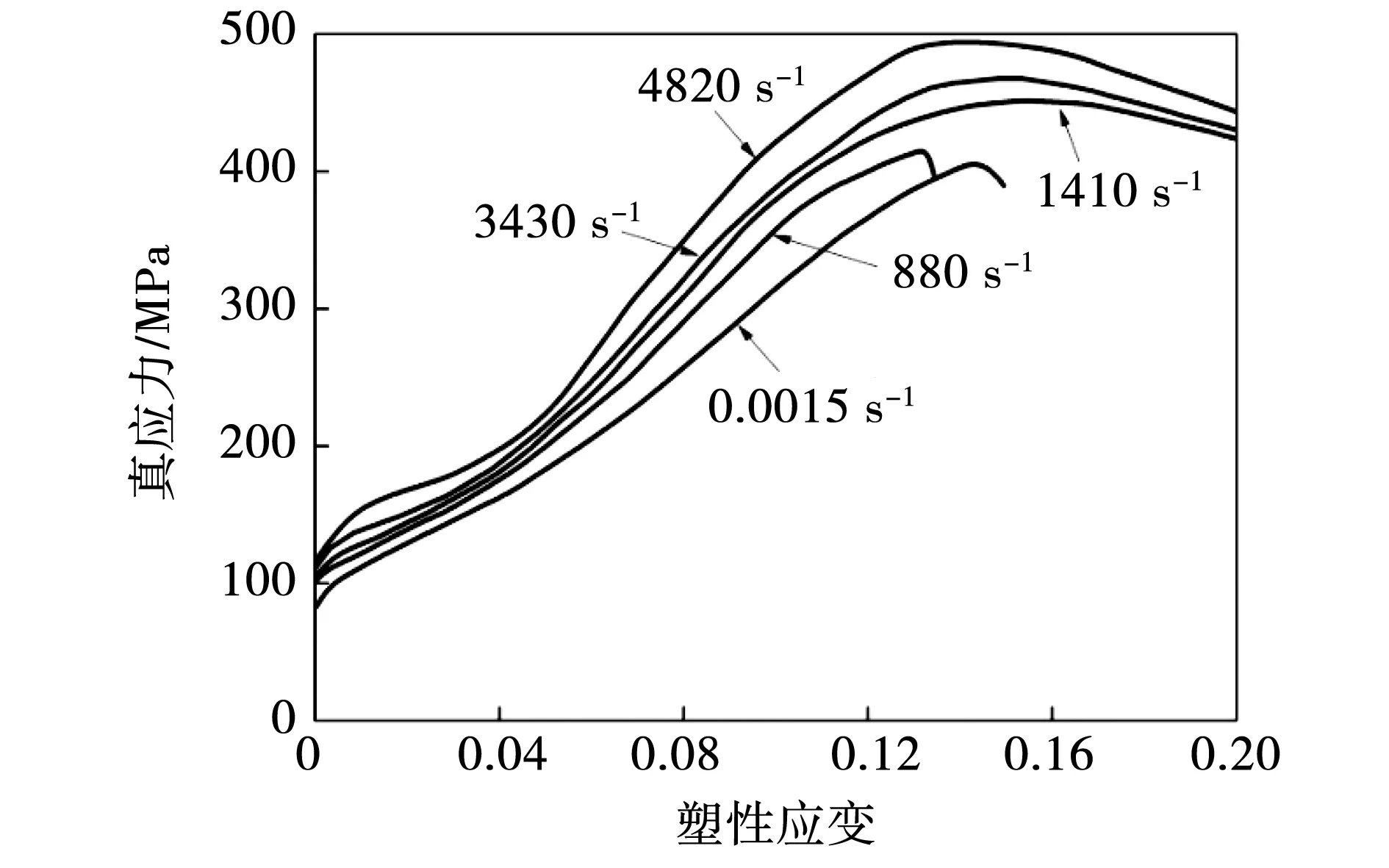
图3 真应力-塑性应变曲线Fig.3 True stress-plastic strain curves

当冲击应变速率为880 s-1时，合金的流变应力随应变的增加表现为单调增加，直至断裂失效；当冲击应变速率增加至1 410 s-1及以上时，流变应力先随应变的增加而增加，当达到峰值应力后则随应变的增加而降低，即在冲击变形后期，合金表现出明显的动态软化。高速冲击载荷下，变形响应时间极短，所产生的形变热来不及传递，致使其变形近似为绝热过程。当加载应变速率高于某一临界值时，在绝热温升的作用下位错产生动态回复，甚至还会诱发绝热剪切带。此时，绝热温升作用下的动态回复和绝热剪切软化效应占主导，流变应力反而随应变的增加而降低。

不同应变速率下，AZ31镁合金棒材的屈服和极限强度如图4所示。由图4可知，在高速冲击载荷下，合金的屈服和极限强度均随应变速率的增加而增加，其值与应变速率近似呈线性关系。为进一步分析AZ31镁合金棒材在冲击载荷下的应变硬化行为，对真应力-塑性应变曲线求一次导，得到不同应变速率下的应变硬化率-真应变曲线如图5所示。由图5可知，高速冲击载荷下的应变硬化率明显高于准静态的。这主要是由于孪生具有较强的应变速率敏感性[18]。不同应变速率下压缩至0.2应变时的变形组织如图6所示，其显微组织中的孪晶密度随应变速率的增加而增加，冲击载荷下的孪晶密度明显高于准静态的。

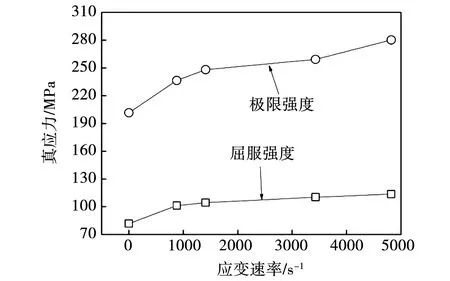
图4 极限强度和屈服强度与应变速率的关系曲线Fig.4 Curves of ultimate strength and yield stress versus strain rates

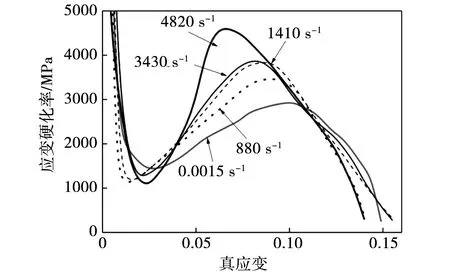
图5 应变硬化率-真应变曲线Fig.5 Strain hardening rate-compressive true strain curves

图6 压缩至0.2应变时的金相图Fig.6 Optical images with compressive strain of 0.2

3 本构建模及分析

J-C本构模型是一种经验型模型，它的适应性较强，参数求解较为方便，广泛地运用于碰撞和爆炸等高应变速率变形的仿真模拟中。J-C本构由3部分组成：应变函数、应变速率函数和温度函数，其表达式[8]：

(1)

式中：

σ—真应力；

A—参考条件下的屈服应力；

B—应变硬化系数；

n—应变硬化指数；

ε—真应变；

C—应变速率硬化系数；

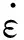
m—温升软化系数；

T*—比温度，T*=(T0-Tr)/(Tm-Tr),其中T0为实验温度，Tr为参考温度，Tm为材料的熔化温度。

本研究中高速冲击均在室温下进行，其表达式可简化为

(2)

首先，选择0.001 5 s-1作为参考应变速率，则在参考应变速率下式(2)则为σ=(A+Bεn)，基于应力-应变曲线得到其屈服强度为87.3 MPa；然后，对等式两边取对数得到ln(α-A)=ln(B)+nln(ε)，通过对ln(ε)和ln(α-A)进行线性拟合得到B=1 528.436 MPa，n=0.854。

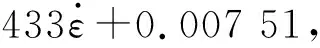
(3)

基于修正J-C本构的拟合结果与实验结果的对比如图7所示。可见，所构建的修正J-C本构模型能够较好地表征挤压AZ31镁合金棒材在高速冲击载荷下的力学响应行为。由于挤压AZ31镁合金在不同应变速率下的应变硬化率与应变大小有关，特别是在中低应变时的应变硬化率相对较低，而所建本构的应变硬化指数n为整个变形过程的均值，故在中低应变下本构拟合应力大于实验应力。

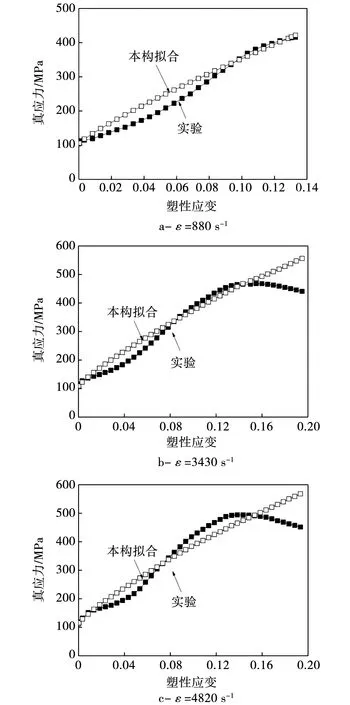
图7 本构拟合与实验结果的对比Fig.7 Comparisons between constitutive fitting and experimental results

4 结 论

1)挤压AZ31镁合金在高速冲击载荷下具有明显的正应变速率敏感性，其屈服强度和极限强度均随应变速率的增加而增加。

2)通过将应变速率硬化系数C修正为应变速率的函数，构建了能够较好表征挤压AZ31镁合金动态力学响应的修正J-C本构模型，本构拟合结果与实验结果基本吻合。