燃气发动机废气再循环随机调节控制器设计
杨君,王明杰,李延骁
1.山东交通学院 汽车工程学院,山东 济南 250357; 2.山东交通学院 机动车检测实验中心,山东 济南 250100
0 引言
本文中建立燃气发动机缸内废气总质量的离散动态模型,设计基于离散动态模型的随机调节器,可调节缸内废气总质量到其设定值的邻域内,并通过仿真计算随机调节器在3种工况下的调节效果。
1 随机调节器设计
设计燃气发动机缸内废气总质量的随机调节器,定义缸内废气总质量与缸内吸入空气质量、喷入缸内燃气质量之和的比值
(1)
式中:k为循环数,mr(k-1)为第k-1循环排气冲程完毕时缸内残余的废气质量,me(k-1)为第k-1循环再循环废气质量,man(k)为第k循环缸内吸入空气质量,λd为理想空燃比,man(k)/λd为第k循环喷入缸内燃气质量。
参照文献[7],定义排气冲程完毕时缸内残余的废气质量与进气冲程完毕时缸内混合气质量的比值
(2)
由(1)和(2)可得:
(3)
令第k循环缸内废气总质量为mEGR(k),即
(4)
将式(4)代入(3)可得:
整整三个月,阿东没有出门,他在家里读书。老巴很高兴,他喜欢儿子这样。就算没有赚钱,但读书毕竟是正经事。而且,心里有大志向的人,才会这样去读书。
(5)
式(5)即为缸内废气总质量的离散动态模型。由文献[8]可知,可将r2(k)建模为有限状态齐次马尔科夫链,其一步预测模型为

定义:考虑离散跳变系统
z(k+1)=Λ(r(k))z(k),
(6)
式中:z(k)为系统状态,Λ(r(k))为系统矩阵,r(k)为有限状态齐次马尔科夫链。若对于任意的初始条件(z(0),r(0)),存在一个有限界Ω(z(0),r(0))>0,使得
式中E为期望算子。则称系统(6)是随机稳定的。
引理:对于系统(6),若对于给定的正定对称矩阵Φ(ri)>0,i=1,…,N,存在正定矩阵γ(ri)>0,i=1,…,N,使得
式中pij为r(k)的一步转移概率,则系统(6)是随机稳定的。
定理:对于缸内废气总质量的离散动态模型(6),设计再循环废气质量
(7)

证明:选取李雅普诺夫函数为
(8)
其中c(si)>0为设计参数。对(8)取差分,可得
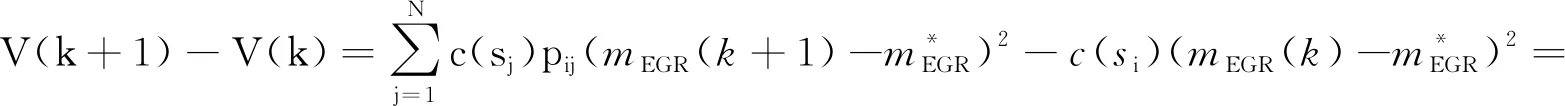
(9)
将(7)代入(9)可得
因此,由引理可知,由(6)和(7)组成的闭环系统是随机稳定的。
2 数值仿真验证
对设计随机调节器(7)的数值仿真验证。基于缸内废气总质量的离散动态模型(5)和文献[11-14]中的均值模型,搭建了如下具有EGR系统的燃气发动机数值仿真模型:


式中:s为函数ψ(s)的自变量,k为比热比。数值仿真结构如图1所示。

图1 数值仿真结构图
数值仿真在3种工况下运行,3种工况的具体参数如表1所示,3种工况下的缸内废气总质量和再循环废气质量如图2~7所示。

表1 数值仿真工况

图2 C1工况下缸内废气总质量 图3 C1工况下再循环废气质量

图4 C2工况下缸内废气总质量 图5 C2工况下再循环废气质量
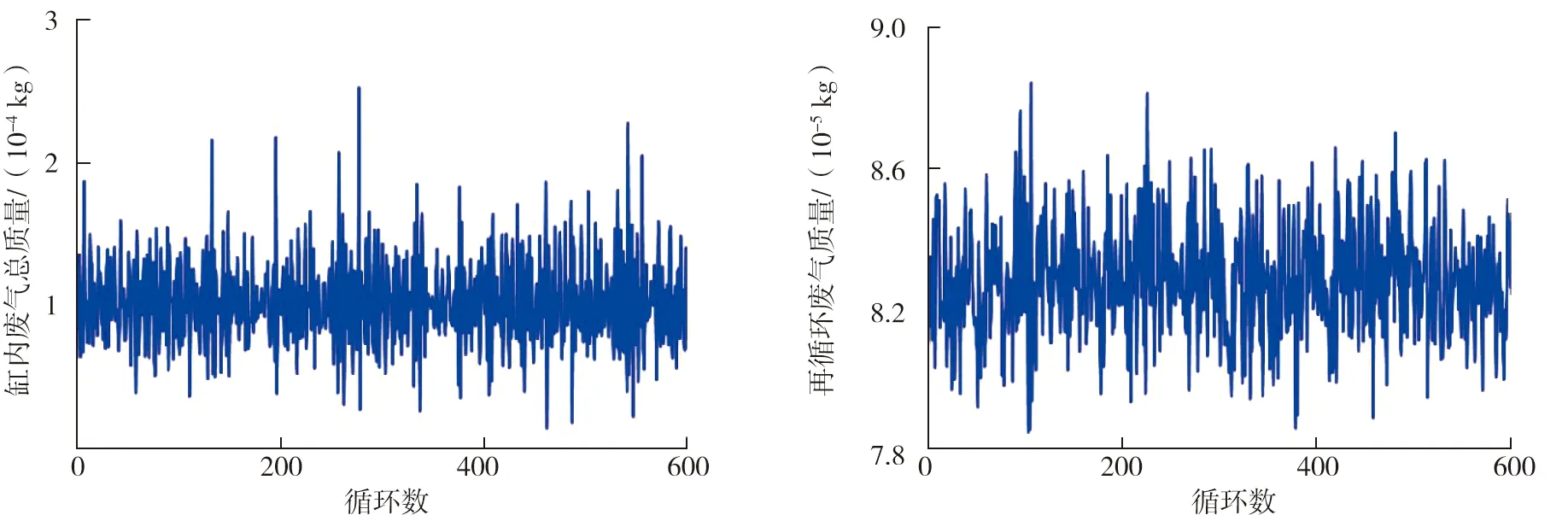
图6 C3工况下缸内废气总质量 图7 C3工况下再循环废气质量
由图2~7可知,所设计的随机调节器(7)在C1、C2、C3三种工况下均能将缸内废气总质量调节到其设定值的邻域内,且再循环废气质量有界。
3 结论
1)建立了缸内废气总质量的离散动态模型。
2)基于建立的离散动态模型,设计了缸内废气总质量的随机调节器。
3)通过数值仿真验证了所设计随机调节器的有效性,即在3种工况下均能将缸内废气总质量调节到其设定值的邻域内。

