核电厂蓄电池直流系统短路电流的计算方法及其危害分析

孔凡华，尚艳菲

(福建福清核电有限公司，福建 福州 350318)

随着研究的不断深入，关于交流系统的短路电流计算已是非常清晰和完善。而对于直流系统的短路电流计算，国内虽然已有电力行业的标准[5,8]作为指导，但是对于直流系统短路后的电流变化曲线、短路故障的切除时间仍无明确的描述。

核电厂蓄电池直流系统以其固有的持续供电能力，保证了负载的持续供电，因此，研究直流系统在蓄电池带载工况下的短路电流具有非常重要的意义。本文在参考IEEE及IEC标准的基础上，结合设备选型和金属导线的熔断特性，对短路电流变化曲线、短路故障的切除时间给出了定量分析。

1 核电厂直流系统介绍

一般的，核电厂的直流系统为IT系统[5]，即：电力系统与大地间不直接连接，电气装置的外露可接近导体，通过保护接地线与接地极连接。

一个核电厂的典型直流系统构成如图1所示，由交流电源、充电器、蓄电池、直流母线、负载等共同构成。

图1 电厂直流系统典型图Fig.1 Typical diagram of DC system

2 核电厂直流系统短路类型

直流系统的短路，是指正极和负极之间不经过用电设备，正负极直接连接或通过公共导体连接形成闭合回路的过程。

2.1 正负极直接连接

正负极直接连接是指由于电缆破损、异物侵入、用电设备内部故障等造成的正极和负极直接连接在一起的情况。

2.2 正负极经公共导体连接

正负极经公共导体连接，最常见的是由接地故障引起，正负极通过共用的接地线而形成闭合回路。

核电厂的直流系统为IT系统，如果正、负极只有一极接地时，对直流系统的运行不会产生影响，系统可以持续对下游负载进行供电。

如果单点接地不及时处理的话，同时叠加另一极的一点接地时，正负极将经过共用接地线而短路，会对系统运行产生影响，这种叠加接地的工况统称为多点接地。

3 蓄电池直流系统短路电流计算

3.1 直流系统短路电流影响因素

在IEC中明确了核电厂和变电站的直流系统短路电流准稳态计算方法[4]，并指出了对直流系统短路电流产生影响的4种来源：

1)频率为50 Hz或60 Hz的三相交流电桥整流装置；

2)固定型铅酸蓄电池组；

3)滤波电容；

4)直流电动机。

如果在直流系统中只有一种来源，那么短路电流计算时，只需要考虑单一来源的影响即可。如果有多种来源，那么在短路电流计算时，均要考虑在内。

3.2 蓄电池直流系统短路电流计算方法

本文只分析蓄电池带载工况下的短路电流，因此，不计及充电装置、滤波电容、直流电动机等的助增电流，IEC中，定义了公式(1)及参数。

RBB=0.9RB+RBL+RY

LBB=LB+LBL+LY

(1)

式中，RB——短路情况下的蓄电池内阻，一般由制造商给出。如果对于一个放电结束状态蓄电池的内阻RB未知的话，可以使用正常充电蓄电池的内阻乘以1.7的系数来确定;

LB——短路情况下的蓄电池电感。如果包含连接导体部分的单节蓄电池的电感没有明确值的话，可以使用L=0.2 μH;

RBB——短路情况下蓄电池回路所有元件电阻;

LBB——短路情况下蓄电池回路所有元件电感;

RBL——蓄电池回路的导体电阻;

LBL——蓄电池回路的导体电感;

RY——负载回路的电阻;

LY——负载回路的电感;

EB——蓄电池开路电压，如果开路电压未知的话，可以按照U=2.0 V/节乘以蓄电池数量N进行计算。一般的，可以假定充满电的蓄电池为EB=1.05NU，未充电或放电结束的蓄电池为EB=0.9NU。

仅蓄电池供电工况下短路电流的变化趋势，如图2所示，在短时间内达到短路电流峰值，然后电流会逐渐减小至准稳态短路电流，并由蓄电池的持续供电，直至蓄电池电量耗尽或其他原因摆脱短路工况：

图2 短路电流与时间的近似函数关系[4]Fig.2 Standard approximation function relationship between short-circuit current and time注：ip—短路电流峰值；tp—到达短路电流峰值的时间；Ik—达到准稳态时的电流；τ1—上升时间常数；τ2—下降时间常数；Tk—短路电流的持续时间

准稳态短路电流为：

(2)

短路电流峰值为：

(3)

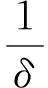
(4)

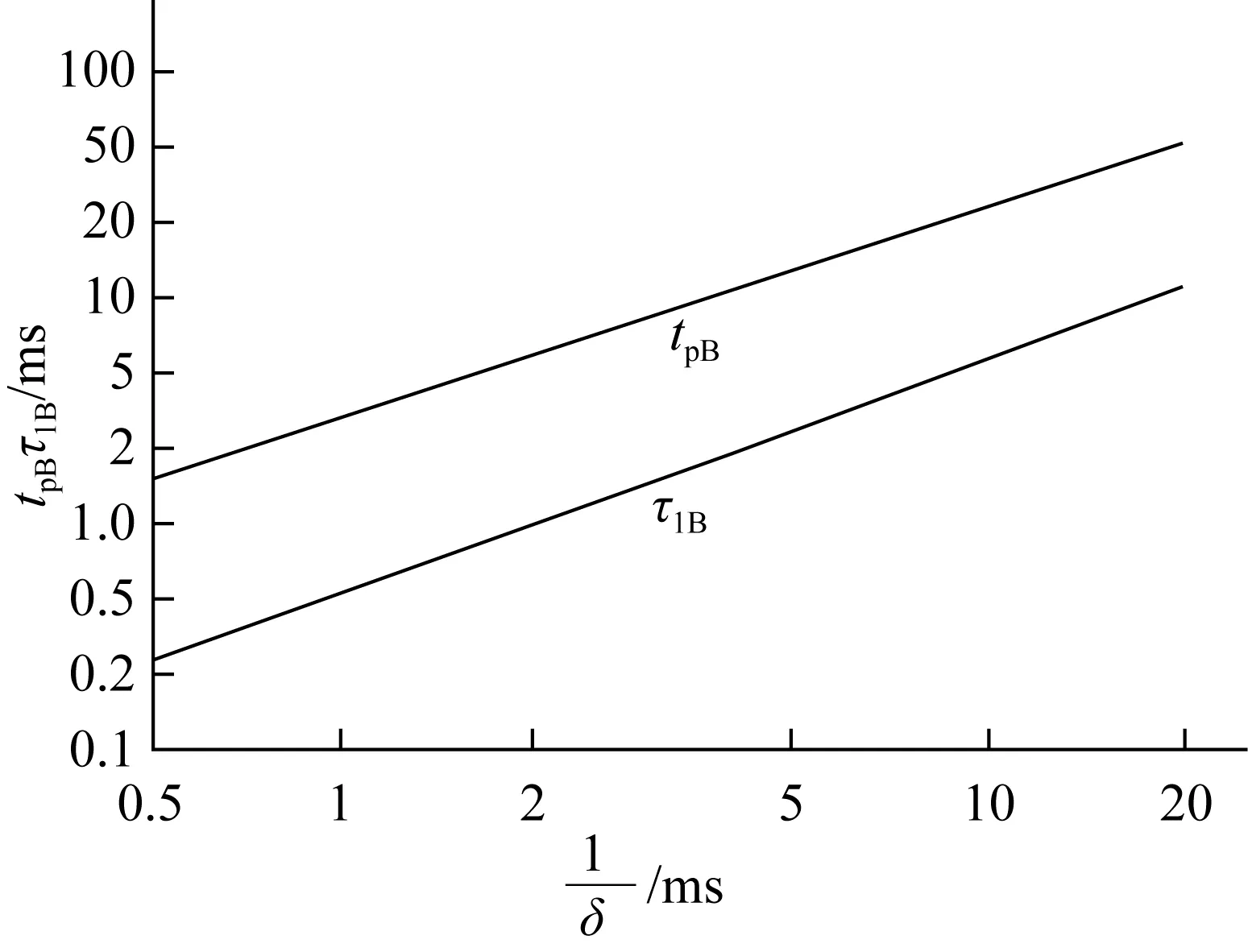
图3 到达峰值电流的时间tpB、上升时间常数τ1B、下降时间常数τ2B与之间的函数关系[4]Fig.3 Time to peak tpB and rise time constant τ1B as a function of

下降时间常数τ2B假定为一个固定值：

τ2B=100 ms

(5)

4 不同短路点短路电流计算

通过上文的分析，不管是由于多点接地造成正负极之间短路，还是正负极之间由于其他原因短路，最终都是通过产生的电流，进而引起电压的变化而造成影响。本文中对蓄电池直流系统短路电流进行计算和分析，旨在提供一种直流系统的短路电流的计算方法，并进而提高直流系统的稳定性和供电可靠性。使得直流系统的短路，从如何形成、如何发展，到最后有何影响进行清晰、准确的描述，降低对直流系统多点接地、系统短路的恐惧。

本文进行计算时，以图4的48 V直流系统为例，对于其他电压等级的短路电流计算，方法是相同的。

图4 蓄电池短路计算等效电路图Fig.4 The equivalent circuit of battery short circuit calculation

4.1 蓄电池出线端短路-故障点FB

按照图1给出的信息，可得：

RB=0.45×23=10.35 mΩ

LB=0.2×23=4.6 μH

在不计短路点的接触电阻时，得出：

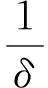
τ2B=100 ms

τ1B=0.52 ms

tpB=3 ms

即蓄电池出线侧出现正负极短路问题时，将在3 ms内达到峰值电流4 923 A，若短路持续发展，蓄电池能持续供电，且保护均不动作、导线均未熔断的情况下，则最终的短路准稳态电流为4 433 A。

但电流的持续时间真的能达到那么长的时间吗？这就取决于回路中的保护动作速度及短路点是否熔断。

本例中讲的是蓄电池出线侧正负极短路，在该回路中，并无保护装置，因此，电流会持续，直至蓄电池损坏无法供电或短路点熔断。

根据参考文献[9]，计算直接引用公式：

(6)

进而推导出：

(7)

式中：J——短路部位电流密度，单位A/mm2;

S——短路点接触面积，单位mm2;

t——短路电流持续时间。

由于短路点并不是正负极的导线的全接触，更多故障情况下是点接触。在点接触时，由于接触面积小，因此，电流密度大，导线会由于熔断而断开连接，假设短路部位截面积为1 mm2时，按照准稳态短路电流计算短路点熔断时间为：

假设短路部位截面积为4 mm2时，按照准稳态短路电流计算短路部位熔断时间为：

但当短路部位截面积>6.81 mm2时，由于电流密度已小于651 A/mm2，此时，短路电流可能会持续存在，短路点可能不会熔断，直至被人为断开或蓄电池电量放尽。

在实际工作中，短路接触部位为点接触，接触面积都很小，在短路部位熔断后，由于重力或导线本身张力等的作用，短路部位碳化等，短路点将断开。本文为定性分析，在进行故障最短切除时间时，选择≤1 mm2作为短路故障点的接触面积。

但是，也应该充分认识到实际故障发生的多样性，短路点并不总是会熔断。例如：短路点由于重力作用而接触时，由于重力作用会随着接触部位的融化接触面积会增大也是有可能的；也可能会存在弹力、浮力等导致的接触，也会存在类似的问题。

同时，也需注意蓄电池短路的危险性：如果未能及时发现并断开的话，由于大电流通过蓄电池，电解液温度会上升，可能会引起人员烫伤。同时，短路点由于接触电阻较大，温度会急剧上升，甚至产生电火花，如果故障点发生在蓄电池正负极的接线端子，可能会引燃蓄电池外壳进而引爆电解液，因此对于这类故障要充分重视。如果故障点不在蓄电池本体，而距离较远时，电解液体温度会上升，通过蒸发可以带走热量，一般不会引发火灾或爆炸。

4.2 开关柜进线端短路-故障点FBL

根据图1中的电缆信息：

RBL=1.1 mΩ

LBL=0.15 μH

在不计短路点的接触电阻时，得出：

短路点熔断时间：

t1=1.5 ms

蓄电池出线至开关柜的回路中配置的NH4a-800 A，gL/gG的熔断器，如短路故障发生在熔断器进线端，由于故障电流不通过熔断体，故熔断器开关无法起到保护作用；若短路故障发生在熔断器的出线端，则根据熔断器的脱扣曲线，在4 007 A故障电流下，其熔断时间约为4 s,通过熔断器熔断可将故障点切除，避免故障点持续放电。

4.3 第一级负载短路—故障点FY1

根据图1的电缆信息，可得：

RY1=131.4 mΩ

LY2=3.04 μH

在不计短路点的接触电阻时，得出：

由于故障电流较小，在接触面积为1 mm2时，短路点不会熔断。

回路中所配置的S262UC-C16的空开，根据其脱扣曲线，在320 A电流下，其脱扣时间≤0.02 s,可将短路点切除。

若出现空开拒动时，此时的故障电流较小，可以有8～10 h去处理短路故障点，对系统影响小。

4.4 第二级负载短路—故障点FY2

根据上图中的电缆信息，可得：

RY2=2000 mΩ

LY2=28 μH

在不计短路点的接触电阻时，得出：

由于故障电流较小，在接触面积为1 mm2时，导线不会熔断。

第二级回路中所配置的为LITTLEFUSE公司1 A的熔断器，在21 A故障电流下，其动作时间为0.001～0.01 s，可迅速将故障点断开。

5 蓄电池直流系统短路危害

通过以上数据的计算和分析，我们可以得出：

1)在蓄电池与熔断器之间发生短路故障时，短路电流大，且无保护装置，只能通过短路点熔断的方式才能切除，若短路点不能熔断时，蓄电池会一直放电，直至被人为断开或电量耗尽；短路时，负载无法维持正常供电电压;

2)在熔断器出线与母线间出现短路故障时，短路电流大，可以通过熔断器切除故障点，但是由于熔断器切除耗时较长，负载会失电，且需人为更换熔丝后才能恢复供电，对负载影响大；如果短路点接触面积小，则可以通过短路点熔断来切除故障点，此时由于故障点的快速切除，失电只有1.5 ms左右，一般不会影响负载的供电;

3)在负载侧出现短路故障时，由于电缆路径长，电阻大，因此短路电流小，无法通过短路点熔断来切除故障，一般通过断路器或负载的熔断器动作来切除故障点，只会对本回路产生影响，不会影响其他负载的供电。

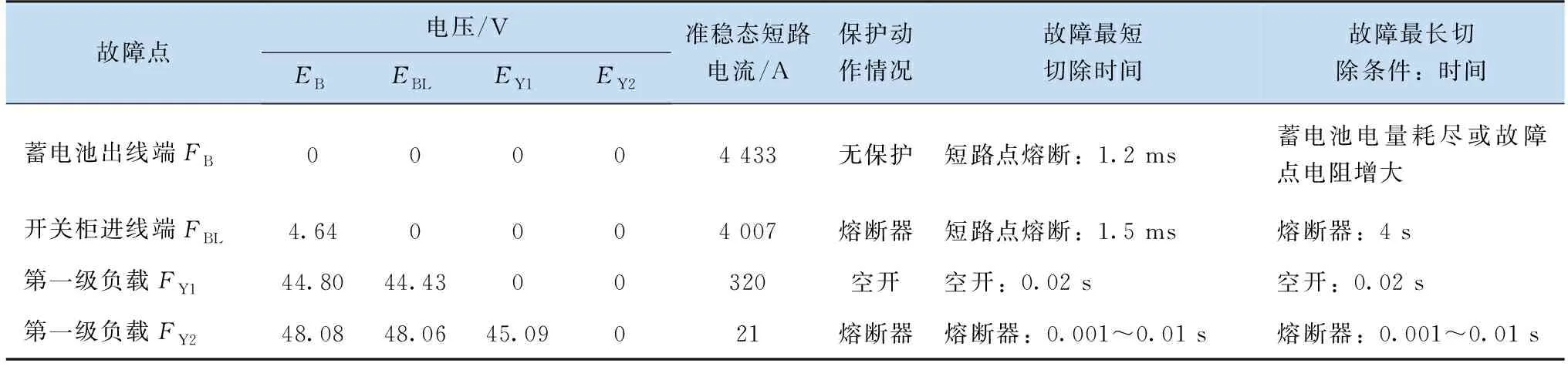
表1 不同短路点危害统计表Table 1 Data analysis of different short circuit points

6 结束语

通过本文的分析和计算，明确了直流系统在短路故障后的保护动作情况和电流变化趋势，从而揭开了直流系统短路的神秘面纱，消除了对短路的盲目恐惧。本文参考相关文献进行实例分析，国内也亟须制定相应的标准或导则，以推广先进分析方法和理念。直流系统短路故障可定量、具体地进行分析，这对故障根本原因分析是有利的，对保障直流系统安全、稳定、可靠运行有着非常重要的意义。