考虑Lode参数影响的Q235B钢循环微孔扩展模型*

赵 威， 黄学伟， 赵 军， 葛建舟

(郑州大学力学与工程科学学院， 郑州 450001)

0 引言

钢结构施工方便、重量小、成本低等优点，使其得到了普遍应用，在抗震设防地区，由于强烈地震作用引起的钢材超低周疲劳断裂是钢结构设计和研究中的重要问题。在超低周循环荷载作用下，钢材产生很大的塑性变形，并且超低周疲劳寿命很低(一般少于20周次)。在微观机理上，钢材的超低周疲劳断裂是由微孔洞的形核、扩展以及聚合引起的延性断裂破坏[1]。传统的断裂力学假设宏观裂纹在材料或结构中已存在，并且在分析断裂问题时裂纹尖端存在着较高的应变约束情况，因此这种方法不适合于微孔洞扩展引起的超低周疲劳断裂[2]。

近年来，国内外学者对于钢材微观机制断裂预测模型开展了较多的研究，用于单调加载情况下的断裂模型，比较典型的有微孔扩展模型(VGM模型)[3]、应力修正临界应变模型(SMCS模型)[4]和GTN模型[5-6]。Kanvinde和Deierlein[7]通过试验和有限元分析验证了SMCS模型和VGM模型能够预测钢结构节点在单调荷载下的裂纹起始。Kanvinde[8-9]等把微孔扩展模型推广到超低周循环加载的情况，提出了循环空隙增长模型(CVGM模型)和退化有效塑性应变模型(DSPS模型)。Kanvinde和Fell[10]等将CVGM模型用于钢支撑构件的超低周疲劳断裂预测，结果也证明了CVGM模型预测实际钢结构节点断裂的能力。黄学伟[11]等基于细观损伤断裂模型对于梁柱焊接节点的超低周疲劳断裂进行了预测分析，取得了良好的预测结果。但以上这些断裂预测模型都是只考虑了应力三轴度对钢断裂的影响，而没有考虑到表征剪切效应的Lode参数对于断裂破坏的影响。工程中对于拉伸和剪切混合型以及剪切型主导的节点断裂模式，剪切效应不可忽略，有必要考虑到Lode参数的影响。

本文以常见的Q235B钢材为例，加工了一批表征不同应力状态的试件，开展了试件的单调加载和超低周疲劳试验，并结合扫描电镜试验和有限元分析，提出了考虑Lode参数的Q235B钢循环微孔扩展模型，并应用该模型预测分析了带缺口平面应变试件的超低周疲劳断裂过程。

1 研究方法

Rice和Tracey[3]研究了应力三轴度和塑性应变对空隙增长和裂纹扩展的影响，提出了微孔扩展模型(VGM模型)来预测单调荷载下材料的断裂破坏：

(1)

在一个特征长度范围l*内，当材料的微孔扩展指数VGI达到临界值η时，延性裂纹在这个特征长度范围内起始。

从式(1)可以看出，VGM模型仅考虑了应力三轴度对材料断裂的影响，而材料某点处的应力状态是由应力三轴度和Lode参数共同表示的。应力三轴度为平均应力与von Mises等效应力之比，Lode参数表示主应力之间的相对方位，如图1所示，图中给出了Haigh-Westergaard主应力空间中的L直线以及π平面。π平面上的任一点的位置可以用σm，σe，r三个应力不变量来表示：

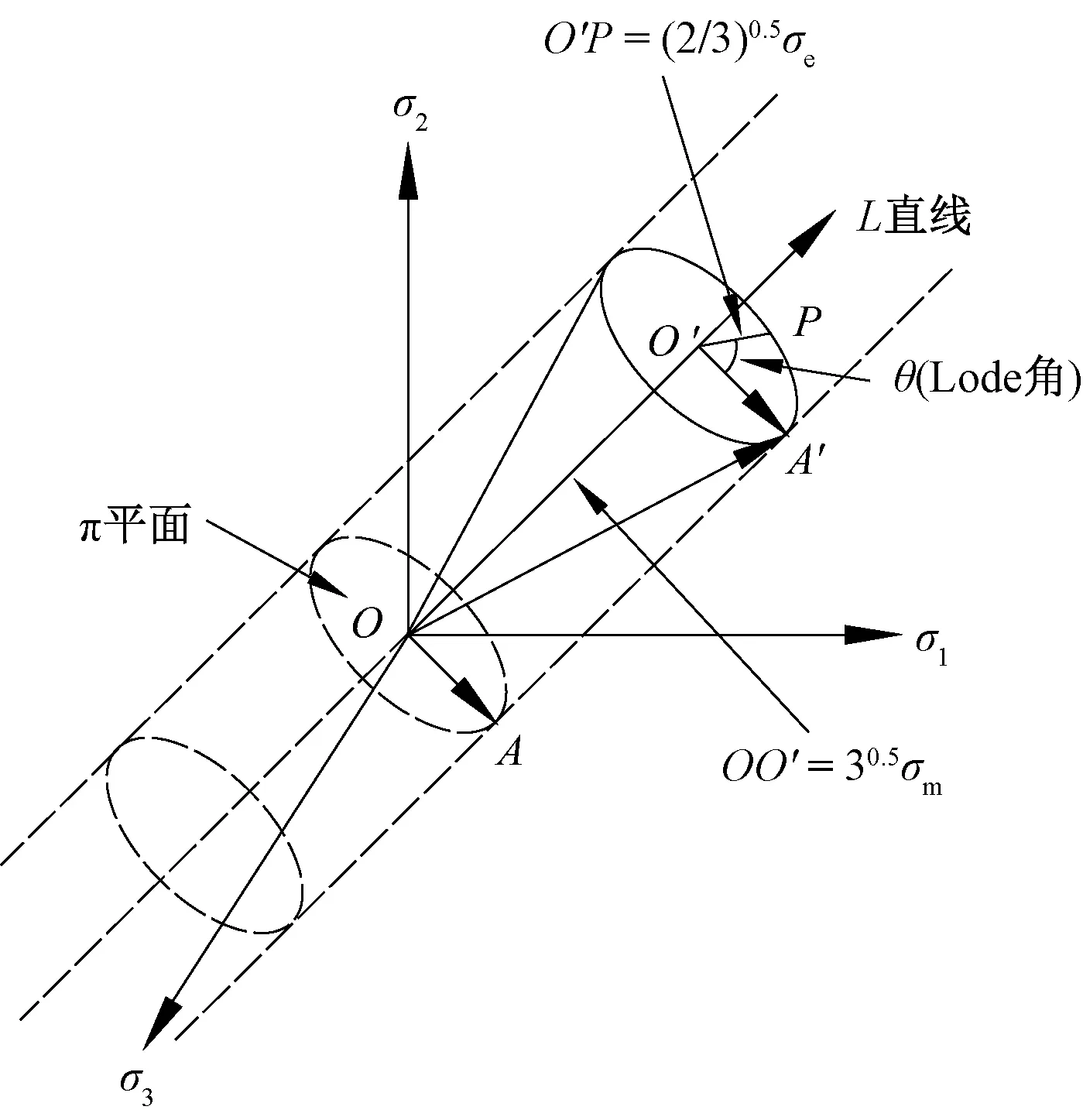
图1 主应力空间坐标系

(2)

(3)

(4)

式中：σ1，σ2，σ3为三个主应力；I1为应力第一不变量；J2，J3分别为第二、第三应力偏量不变量。

而Lode角度θ与第三应力偏量无量纲化的值有关。

cos(3θ)=(r/σe)3

(5)

式中Lode角度θ的取值范围是0≤θ≤π/3。

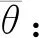
(6)

由式(1)可以看出，在单轴拉伸情况下VMG模型仅考虑了应力三轴度的影响，应力三轴度可以看成是第一主应力不变量的无量纲化，因此该模型适用于高应力三轴度情况下微孔洞扩展引起的断裂破坏。Lode参数与第三应力偏量的无量纲化有关，其在微观上反映了微孔洞的形状变化，微孔洞形状改变对材料的断裂破坏也有重要的影响。本文在VGM模型的基础上，考虑Lode参数对材料断裂破坏的影响，提出考虑Lode参数影响的微孔扩展模型(LVGM)：

(7)

式中：β为考虑Lode参数影响的材料参数，当β=1时，LVGM模型不考虑Lode参数的影响，该模型退化为VGM模型。

在超低周循环荷载作用下，钢材中的微孔洞在受拉时扩展，在受压时收缩，当其微孔洞尺寸达到临界值时材料发生断裂。相对于单调加载，超低周疲劳荷载作用下钢材微孔洞尺寸的临界值会降低，降低的程度可用指数形式的损伤函数来表示，因此循环微孔扩展模型(CVGM模型)的表达式如下：

(8)

式中CVGI为循环微孔扩展模型指数。

为了考虑Lode参数对于超低周循环加载下的Q235钢材的影响，在循环微孔扩展模型(CVGM模型)的基础上，本文提出了考虑剪切效应的循环微孔扩展模型(LCVGM模型)：

(9)

式中：LCVGI为循环微孔扩展指数；ηcycle为循环加载时的微孔扩展指数临界值，它与单调加载下的微孔扩展指数临界值εp的关系为：

ηcycle=ηexp(-λεp)

(10)

式中λ为材料参数。

在超低周循环荷载作用下，压向的循环荷载使得微孔洞尖锐化，使得材料再次受拉时微孔洞扩展迅速，因此可以认为循环加载时的微孔扩展指数ηcycle主要与压向的塑性应变有关。因此式(10)中的εp为受压循环过程中的等效塑性应变的累积，当λ=1时，LCVGM模型可退化为CVGM模型。在一个特征长度范围l*内，当材料的微孔扩展指数LCVGI达到临界值ηcycle时，延性裂纹在这个特征长度范围内起始。

2 试验设计

试件取自厚25mm的Q235B热轧钢板，其化学组分如表1所示。共制作3类试件来进行单调加载和超低周疲劳试验，包括缺口圆棒试件组(NR1，NR3，NR6，每组有3个试件)、缺口平面应变试件(PSN1)和纯剪切试件(PS)，试件形状和尺寸如图2所示，编号如表2所示。使用MTS伺服轴向疲劳试验系统进行加载，分别采取以下两种加载方式：单调拉伸至破坏、等幅循环加载(CTF)直至破坏，具体加载方案如表3所示，单调加载试验过程采用作动器的位移控制，等幅循环加载采用轴向应变控制。试件的长度均为130mm，试件的上下夹持长度均为40mm，应变引伸计的标距为25mm，缺口圆棒试件和缺口平面应变试件引伸计对称放置在易断裂部分的两侧，纯剪切试件(PS)引伸计的位置如图2(c)所示，试验加载装置如图3所示。

Q235B钢材的化学组分/% 表1

Q235B钢材试件编号 表2

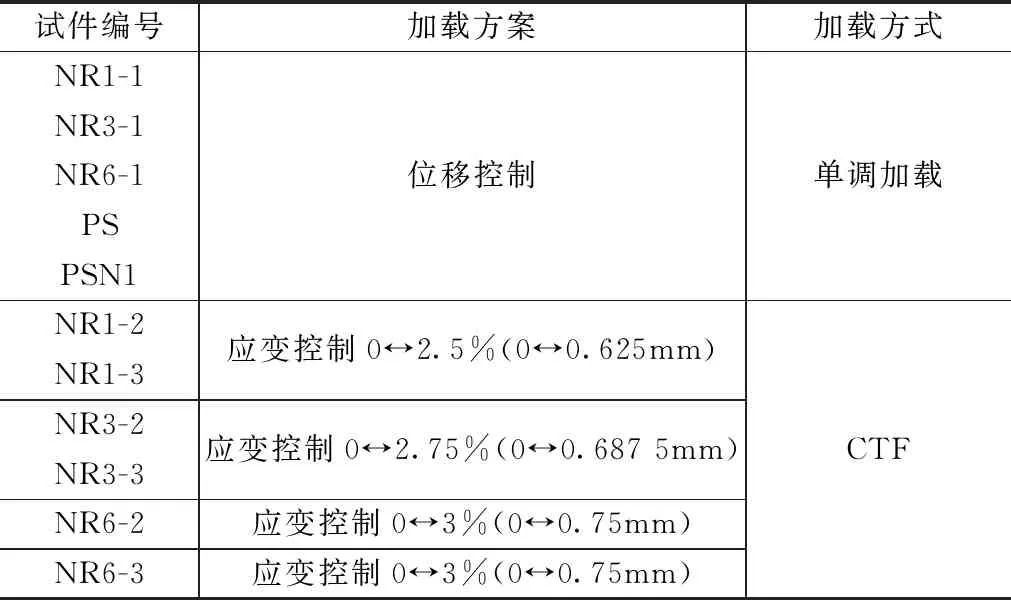
Q235钢材的具体加载方式 表3

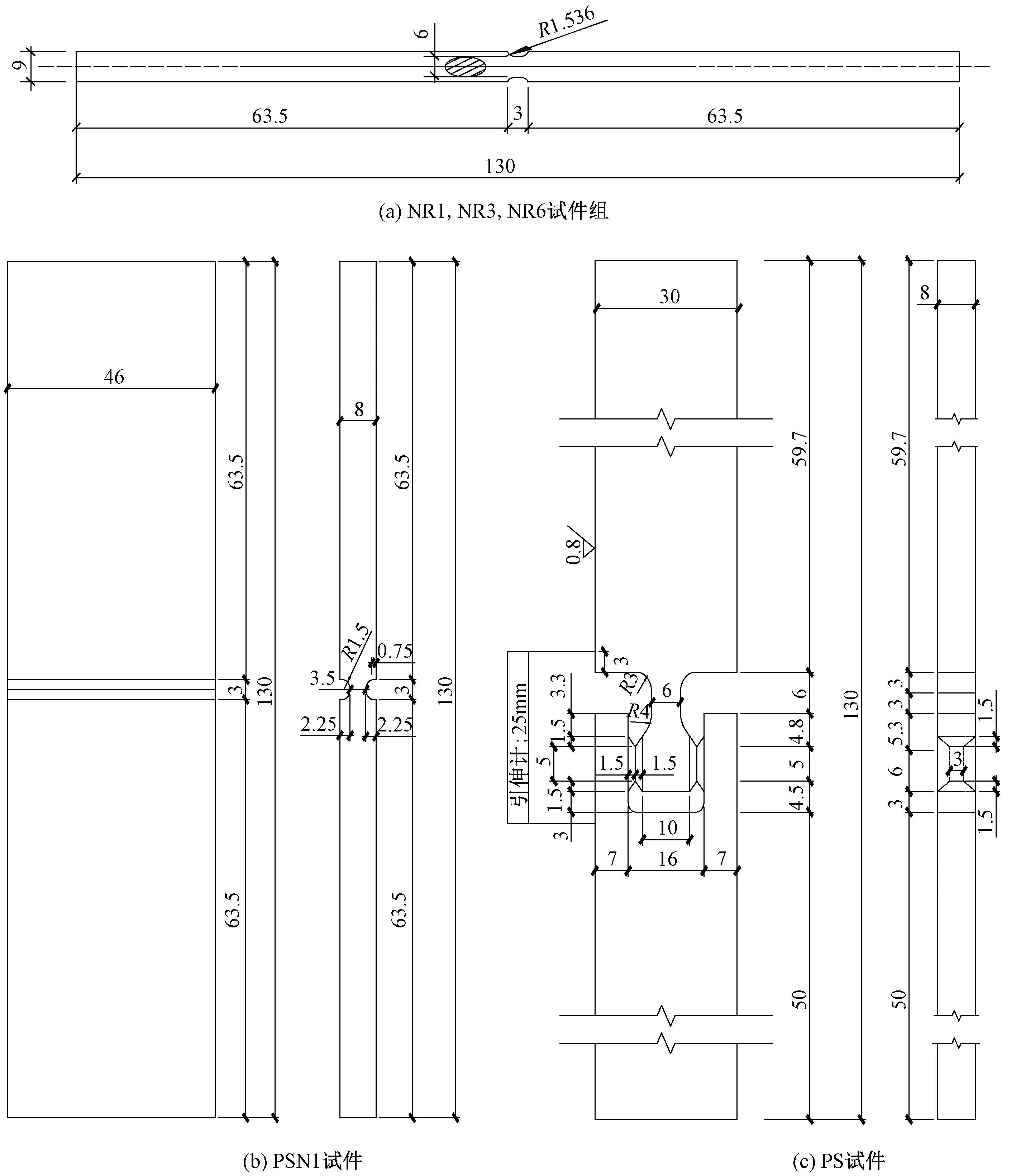
图2 Q235B钢材试件的几何尺寸图

图3 加载细节图

3 试验结果

选择Q235B的缺口圆棒试件、缺口平面应变试件和纯剪切试件，开展试件的单调拉伸试验。在单调加载试验中，各类试件的裂纹起始位置如图4所示。缺口圆棒试件的裂纹起始位置是在最小截面的中心位置，纯剪切试件的裂纹起始位置在V型口顶部的中间位置，而缺口平面应变试件的裂纹起始位置在图4中显示。

选取缺口圆棒试件开展超低周疲劳加载试验，各个试件的裂纹起始位置与单调加载试验中裂纹的起始位置大致相同。在超低周疲劳试验加载过程中，由于NR3-2试件设置的幅值较大，循环6周之后发现该试件被压屈，第7周将其单调拉伸至破坏。各个试件的破坏周次如表4所示。

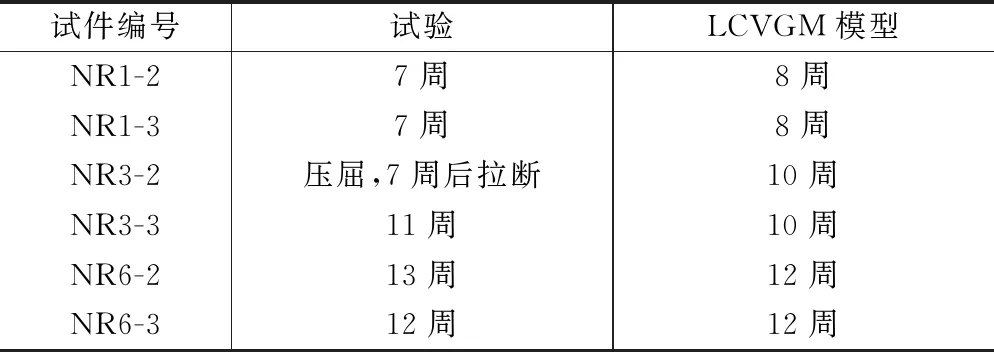
试验与LCVGM模型计算试件疲劳寿命结果对比 表4

图4 Q235B钢材试件的裂纹起始位置

选择典型的Q235B钢材试件，使用扫描电镜观察试件断口的微观形貌，如图5所示。可以看出单调荷载作用下NR6-1试件呈现出明显的等轴韧窝，PSN1-1试件断面中既有剪切韧窝又有等轴韧窝形式，PS-1试件则呈现出剪切韧窝为主的破坏形式。在超低周循环荷载作用下NR6-1试件也呈现出明显的等轴韧窝，因此Q235B钢材在不同的应力状态下呈现出韧窝形式的延性断裂。

图5 Q235B钢材试件的断面图

4 有限元分析和参数标定

通过大型有限元软件ABAQUS对Q235B钢材试件进行有限元计算，分析Q235B钢材应力三轴度、Lode参数与等效塑性应变之间的关系。对缺口圆棒试件，采用轴对称单元建立有限元模型；对缺口平面应变试件，则采用实体单元建立有限元模型；对于纯剪切试件，为了减少计算，则利用对称性只建立一半有限元模型并在对称面上添加对称约束，各个试件有限元模型如图6所示。在数值模拟计算中，材料考虑非线性和等向强化模型，并将试件的易断裂区域的网格划分大约在0.35mm左右，其值与Q235B钢材的特征长度l*相当[12]。

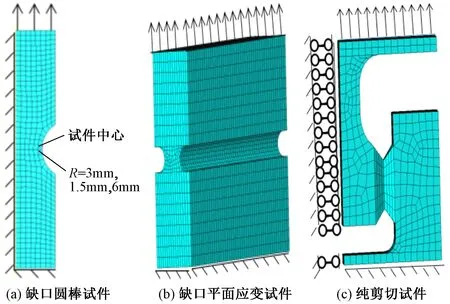
图6 Q235B钢材试件的有限元模型

Q235B钢材的应变强化模型可采用Chaboche非线性等向强化随动强化混合模型，该模型包含非线性随动强化部分和非线性等向强化部分，随动强化部分和等向强化部分的演化方程分别如式(11)，(12)所示。

(11)

(12)

基于Q235B缺口圆棒试件的超低周循环加载的荷载-位移曲线结果标定得到钢材的强化模型参数，如表5所示。基于表中的强化模型参数，得到试件的荷载-位移曲线有限元计算结果与试验结果的对比如图7所示，可以看出有限元计算结果与试验结果一致。

Q235B钢材的强化模型参数 表5

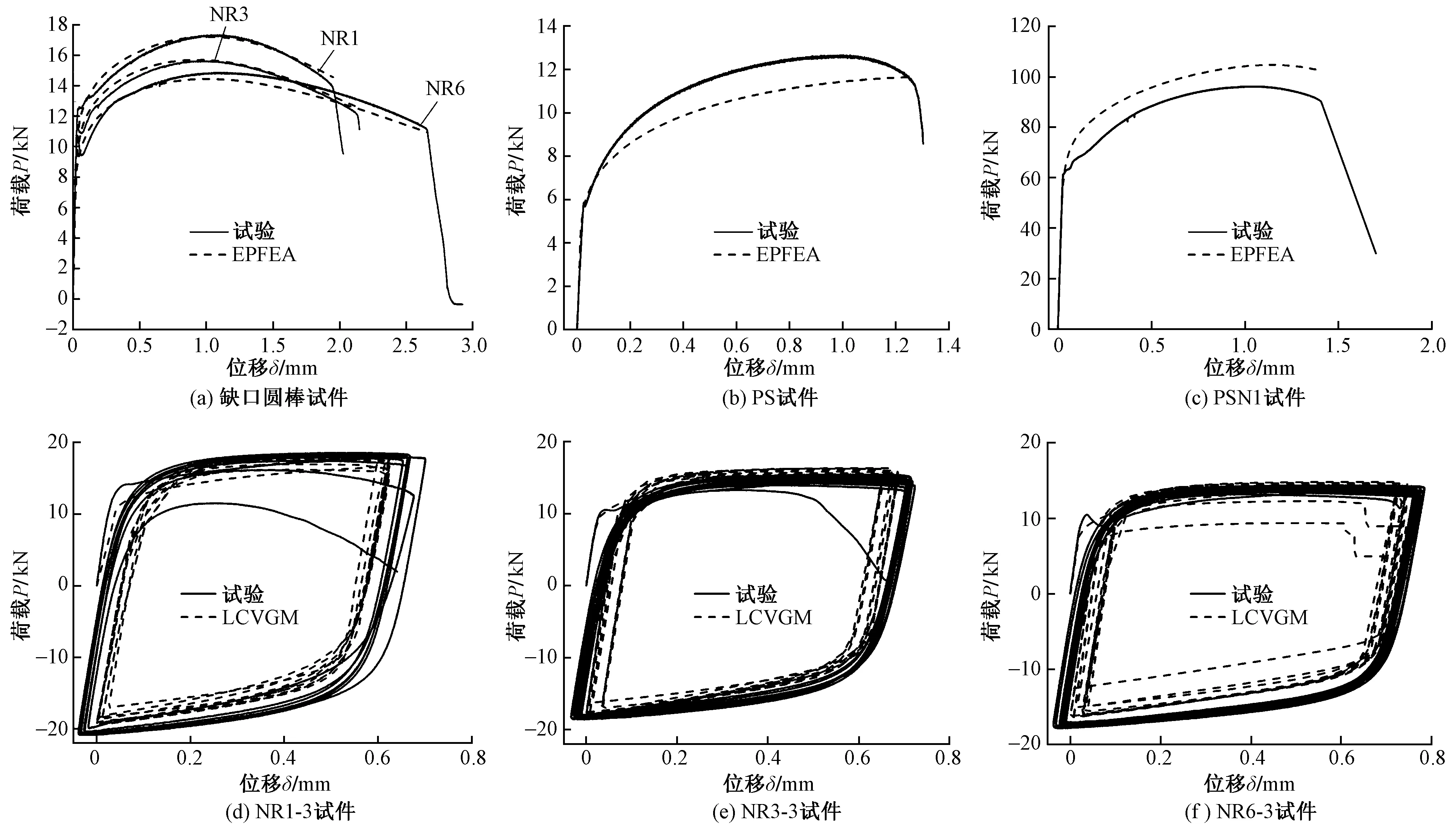
图7 Q235B钢材试件的荷载-位移曲线

标定LCVGM模型的参数分三步：1)根据缺口圆棒试件的单调拉伸试验结果标定出参数η；2)利用缺口平面应变试件和纯剪切试件的单调拉伸试验结果标定出参数β；3)基于缺口圆棒试件的超低周循环加载破坏试验标定参数λ。图7给出了单调加载工况下缺口圆棒试件和板状试件的单调拉伸荷载-位移曲线，图中曲线的斜率突变点可以认为是裂纹起始的时刻。利用ABAQUS软件的弹塑性有限元分析方法(EPFEA)，对缺口圆棒试件的单调拉伸试验进行有限元计算，结果表明裂纹起始的位置，即试件最小截面的中心处的Lode参数为1，这时的LCVGM模型在单调加载工况下可以退化为VGM模型，只要将缺口圆棒试件中心单元从开始加载到裂纹起始时的应力三轴度和等效塑性应变的变化过程代入式(1)左侧即可标定出参数η。

参数η标定完成后，对板状试件的单调拉伸进行弹塑性有限元计算，同样将板状试件裂纹起始位置从开始加载到裂纹起始时的应力、应变历程数据代入式(7)中即可标定出参数β，最终标定得到的参数列入表6中。

材料参数η和β的计算结果 表6

为标定材料参数λ，借助ABAQUS软件中的用户子程序USDFLD，并用Fortran语言将LCVGM模型进行编程，将程序用于缺口圆棒试件的超低周疲劳数值模拟。在数值计算过程中，当材料单元达到破坏准则要求时，将该单元的弹性模量设为1，来判定单元破坏，并按照当前状态继续进行有限元计算至试件破坏。利用后处理云图(图8)可以判断裂纹的起始位置和扩展方向，当设置的状态变量SDV1大于1时，单元破坏。通过在有限元分析中不断调整λ的取值，直至有限元计算的破坏循环周次与试验所得的破坏循环周次接近，最终取得λ=0.27，LCVGM模型计算得到缺口圆棒试件的疲劳寿命与试验寿命对比由表4给出，计算得到缺口圆棒试件的荷载-位移曲线如图7所示，由图可知，有限元计算结果与试验结果的吻合很好。

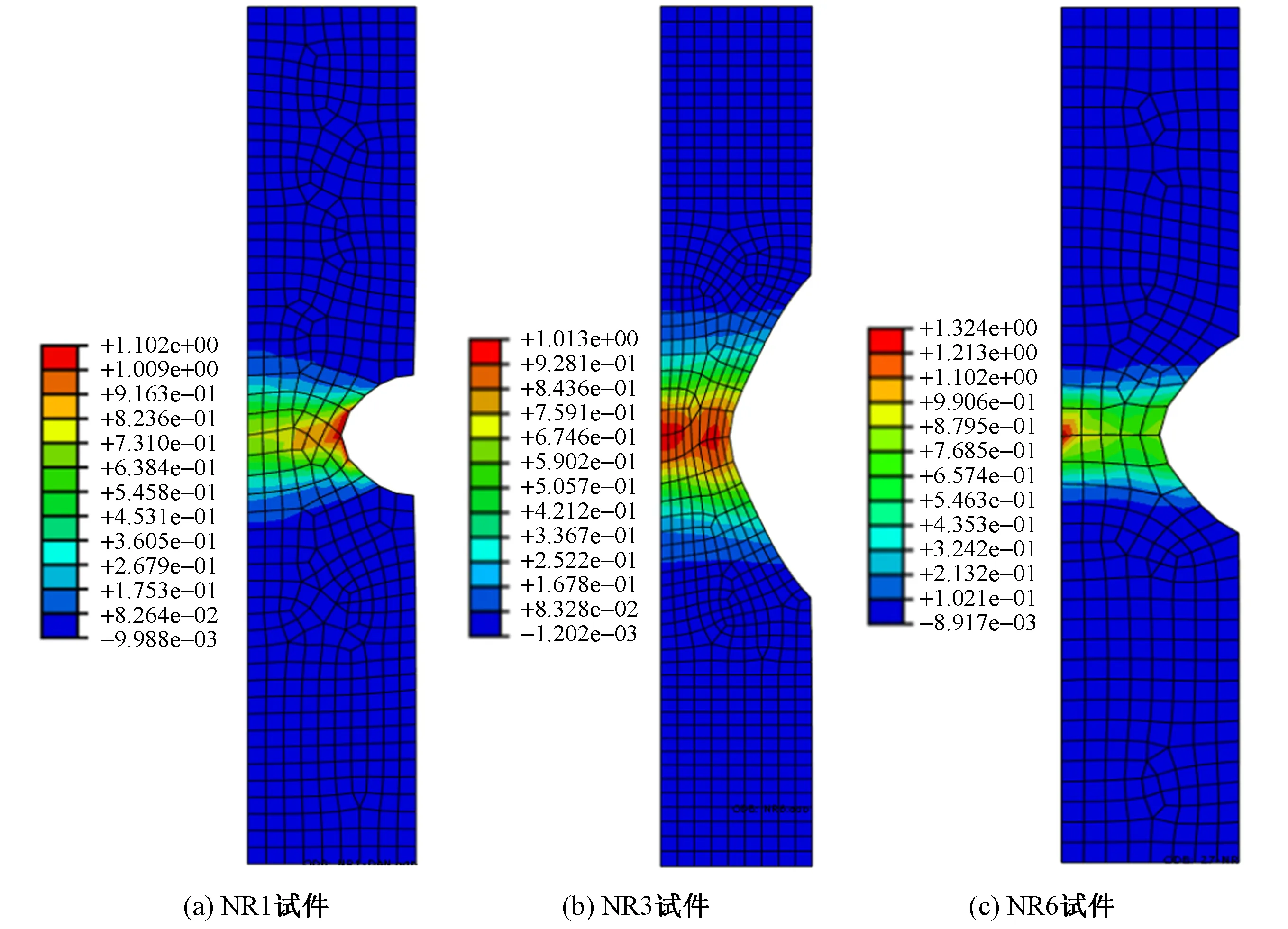
图8 后处理云图

5 平面应变板状试件的破坏预测分析

为进一步证明LCVGM模型的准确性，制作加工两个平面应变板状试件(PSS)，进行超低周疲劳试验，来对模型进行验证分析。试件的尺寸大小如图9所示，引伸计的加持位置对称分布在凹槽的两侧。用ABAQUS对PSS试件进行有限元建模，有限元模型如图10所示，并基于LCVGM模型和CVGM模型进行有限元计算，模拟分析出PSS试件的超低周疲劳断裂过程。通过有限元计算得到的荷载-位移曲线和试验所测得荷载-位移曲线如图11所示。从荷载-位移曲线的对比中可以看出，LCVGM模型与实际测得的曲线基本一致，LCVGM模型算得到PSS于15周发生破坏，而试验所测得PSS试件于14周破坏。所以，LCVGM模型的预测结果与试验的吻合度较高。

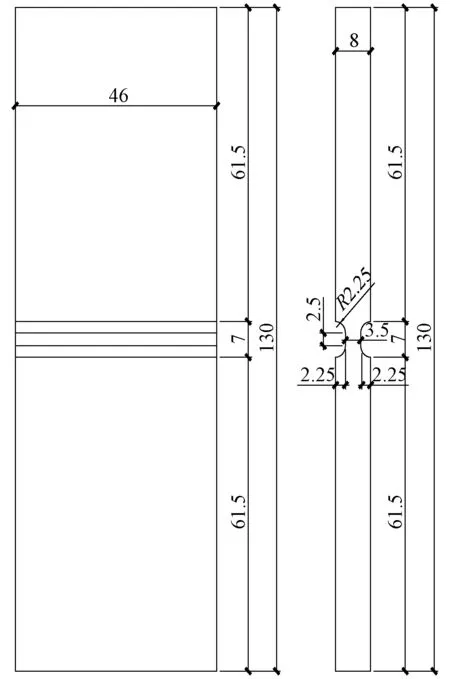
图9 PSS试件的几何尺寸图

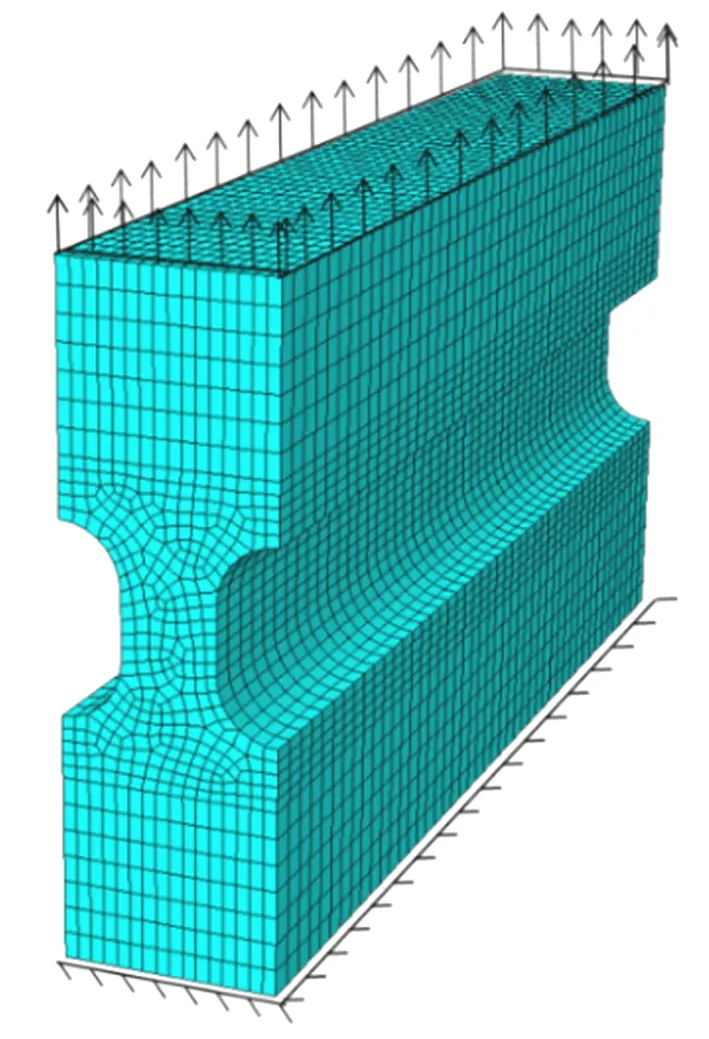
图10 PSS试件的有限元模型

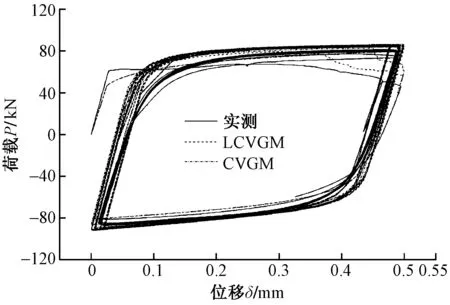
图11 PSS试件的荷载-位移曲线

从图11的荷载-位移曲线可以看出，CVGM模型、LCVGM模型预测的最大荷载都与试验结果相差不大。但在疲劳寿命对比上，CVGM模型预测PSS试件在第16周破坏，因此LCVGM模型的预测结果更加精准。主要原因在于CVGM模型忽略了Lode参数对钢材超低周疲劳破坏的影响，所以CVGM模型的预测结果偏大，不利于工程安全。图12也给出了PSS试件裂纹起始位置，即试件中心处基于两个模型计算得到的损伤发展过程，可以看出，考虑Lode参数影响的LCVGM模型计算得到的循环微孔扩展指数的发展速度明显大于CVGM模型。

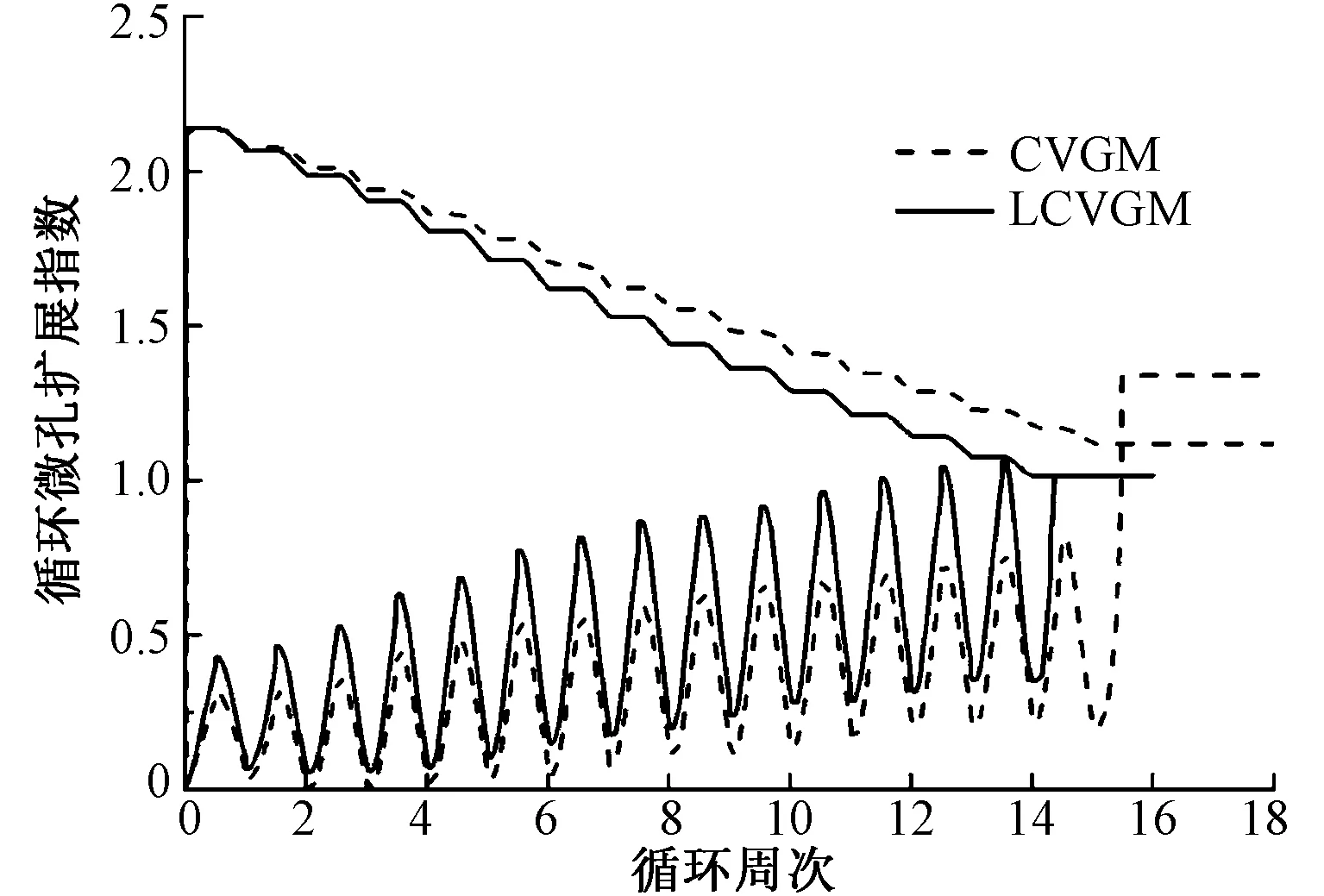
图12 PSS试件的循环微孔扩展指数发展规律

6 结论

(1)对于常见钢材的超低周疲劳断裂破坏，在循环微孔扩展模型(CVGM)的基础上提出了考虑Lode参数影响的断裂预测新模型(LCVGM)。

(2)制作了一批能够表征不同应力状态的Q235B钢材试件，开展了单调拉伸试验和超低周疲劳破坏试验，利用试验结果和有限元分析，标定得到Q235B钢材考虑Lode参数影响的循环微孔扩展模型参数。

(3)利用LCVGM模型对平面应变试件的超低周疲劳破坏进行预测分析，结果表明LCVGM模型比CVGM模型的精度更高而且相对安全。