多机电力系统非线性自适应励磁控制器的设计

刘翠梅

(南宁市三峰能源有限公司，广西 南宁 530021)

1 引言

电力系统输配电的可靠性取决于负荷的波动与发电机功率的有效互补程度，由于电力系统是高度互联的系统，电网中任何部分的负载变化都可能影响整个系统。除了这些负荷变化之外，还有其他一些问题也可能威胁到电力系统的稳定性，如短路故障、雷击过电压、供电能力不足等。最近美国德克萨斯州发生的停电事件证明了发电系统供电能力不足是影响系统稳定性的最好例子。设计合适的励磁控制器可以使电力系统的电压保持恒定，这是电力系统保持稳定的非常重要的方式[1-2]。

近年来，因为传统的线性控制器的运行区间有限，在部分控制域内控制效果未必理想，非线性控制器能够在大范围的运行区域内保持电力系统的稳定动态性能，因此非线性控制器的设计越来越受到关注[3-5]。在文献[6]中，临界参数的变化对电力系统的动态稳定性有很大的影响，阻尼系数、转动惯量和直轴时间常数是影响同步发电机和异步发电机系统稳定性的主要因素。由于非线性励磁控制律包含了这些影响稳定性的敏感参数，在励磁控制器的设计中，通常采用这些参数的标么值[7]。但是其中一些参数无法直接测量或具有一定的时变性，例如发电机的阻尼系数是不能直接测量，瞬态电抗可能由于磁饱和效应而逐渐发生变化。

在现阶段电力系统励磁控制器的设计中，反馈线性化技术已经得到了广泛的应用。反馈线性化控制器对于参数非常敏感，为了获得预期的控制性能，系统参数的精确值是必须已知，而发电机的机械功率和阻尼系数与电力系统的运行状态相关，是一个随机波动的数值，因此反馈线性化控制器在增强电力系统动态稳定性方面具有较差的鲁棒性。通过设计非线性自适应励磁控制器，在部分系统参数未知的情况下可以进行动态估计励磁参数，能够克服励磁控制器的关于敏感参数的问题。在文献[8]中，励磁控制器的设计考虑了未知参数的动态估计，提高了励磁控制器的稳定性。文献[9-10]提出了非线性自适应反步控制器和基于直接反馈线性化控制的自适应控制技术，在单机的无穷大总线系统(SMIB)中将母线电压和输电线路参数规定为未知参数而不是稳定性敏感的关键参数，提高控制系统的暂态稳定性。在文献[11]中提出了另一种类似的控制方案，用于不考虑任何未知参数的带静止同步补偿器的SMIB系统。但在SMIB系统中使用静止同步补偿器并不是一个经济有效的解决方案。文献[12-13]中提出了非线性自适应反步控制器，该控制器通过采用阻尼系数作为控制变量来抑制多机电力系统的低频振荡问题。

本文旨通过考虑发电机的阻尼系数和机械功率，设计一个多机电力系统的非线性自适应励磁控制器，使电力系统在负荷变化时能够稳定运行。负载的功率变化与原动机传动轴上输入的机械功率有很大的联系，如果电力系统中经常发生负荷连续波动，与之对应的发电机的输入机械功率也要跟随变化。同样，阻尼系数的变化也会影响电力系统的稳定性。根据上述要求设计出励磁控制器旨在解决这些问题，并通过MATLAB/Simulink仿真软件对4机11母线电力系统的其中一条关键输电线路上模拟三相短路故障，对其控制性能进行分析和评估。

2 电力系统动态模型

在多机电力系统中，同步发电机和负荷连与其他设备通过传输线相互连接。为了设计励磁控制器，必须建立励磁系统的动力学模型。一个多机电力系统中有N台同步发电机时，第i台同步发电机的动力学模型可以用下列微分方程表示：

δi=ωi-ω0i

(1)

(2)

(3)

式(1)和式(2)表示发电机转速方程，式(3)表示暂态电动势。第i台同步发电机的电气代数方程为：

(4)

(5)

(6)

(7)

(8)

由式(1)～(3)所表示的多机电力系统的动力学模型也可以用代数式(4)～(8)表示。式(1)～(3)是非线性方程，其中非线性方程(6)和(7)体现dq0坐标系下系统内的电流。

根据式(1)～(8)所示的电力系统数学模型，设计非线性自适应反步控制器。在控制器设计之前，需要对控制方式的数学原理进行讨论。

3 非线性自适应控制策略

根据式(1)～(3)的动力学模型，可以看出电力系统是高度非线性的，而非线性是由于电力系统中各非线性元件相互连接而导致的，并且在电力系统中一些敏感参数的精确测量比较困难。例如，阻尼系数的数值Di是变化的。因此，发电机的阻尼系数可以看作是未知参数，因此可以写成：

(9)

其中,θi1是一个未知的参数，Hi是发电机惯性时间常数，因此需要对设计和实现非线性自适应控制器的目的进行估计。

另一个重要的方面是电力系统中负载的变化具有随机性。为了保持电力系统的稳定运行，必须在发电机输出功率和用户消耗功率之间取得平衡。发电机的输出功率取决于原动机轴承输入到发电机的机械功率Pmi。由于负荷的变化量是随机变化的，很难精准预测，所以可以将输入的机械功率认为是未知量。当输入到发电机的机械功率未知时，可以引入以下定义：

(10)

其中,θi2是另一个未知参数。将所有这些未知参数纳入如式(1)～(3)所示的电力系统动力学模型中，根据自适应控制原理可以写成：

(11)

①在受到严重干扰时，保持多机电力系统的稳定性；

②在系统恢复后，尽量减小端电压和转子转速的跟踪误差。

为了解决这些问题，本文设计了非线性自适应励磁控制器。

4 自适应反步励磁控制器设计

设计非线性自适应反步励磁控制器，以Efdi为励磁控制的输入，定义功率角跟踪误差：

z1i=x1i-x1di

(12)

对功率角跟踪误差求时间导数得：

(13)

其中，假设x2i是代表功率角跟踪误差动态的第一个子系统的虚拟控制变量。另一个变量需要定义转子转速的变化，可以定义为：

z2i=x2i-x2di

(14)

则功率角跟踪误差对时间的导数为：

(15)

为了稳定式(15)所示的速度误差动态，可以将控制李雅普诺夫函数(CLF)表示为：

(16)

对李雅普诺夫函数进行时间求导，将z1i的值代入，可以写成：

(17)

x2di=-k1iz1i,k1i>0

(18)

其中，k1i是一个控制参数，并且恒为正，用于调整输出响应。选择虚拟控制律后，令z2i=0，式(17)可以写成:

(19)

(20)

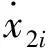
(21)

考虑第二个李雅普诺夫函数:

(22)

(23)

此时，将另一个误差变量定义为z3i=x3i-x3di，如果x3di为：

(24)

则式(23)可以写为：

(25)

k2iz2i)Iqiω0i]=Ai-Bi-Ci+Fiθ1i+Giθ2i

(26)

其中，

最终误差为定义为:

z3i=x3i-x3di

(27)

(28)

式(28)中出现了实际的控制输入Efdi，本设计过程的主要目标是得到实际的励磁控制，使z1i、z2i、z3i在t→∞时收敛到零。

5 仿真分析

以一个广泛应用于动态稳定分析的IEEE双区域4机11母线的电力系统为例，对采用该励磁控制器的发电机稳态性能进行评估。假定图1中多机无穷大系统各发电机的参数都相同，发电机均为同步发电机，其中发电机2(G2)所接母线作为参考母线。系统中所有参数均取标么值，具体参数如下：

图1 双区域4机11母线的电力系统

ωs=1，D=0.1，M=7s，Tdo=8s，U=0.995，Pms=0.15，XT=0.15，Xq=1.76，Xd=1.8，H=4s。

励磁控制器的参数如下：

k1=0.1，k2=0.512，k3=-5.4，T=3s。

母线7与母线9之间的线路用来维持区域1和区域2之间的功率平衡，是两个区域电力系统之间最关键的部分。选择这条特定的关键线路进行三相短路故障进行仿真，来验证所设计的非线性自适应反步励磁控制器(NABEC)的有效性。

将设计的NABEC的性能与文献[13]中提出的现有NABEC(ENABEC)进行比较，其中只有阻尼系数被认为是未知参数。并与传统的电力系统稳定器(CPSS)进行了性能比较。在t=5s时线路发生三相短路故障，当t=5.2s时恢复。考虑了两种情况：

(1)发电机输入机械功率精确已知

在这种情况下，必须考虑输入机械功率Pm的精确值，以便它能与负荷的需求匹配。当母线7和母线9之间的输电线路发生故障时，两个电力系统的稳态将受到干扰。在故障排除后，系统处于稳定状态。而在CPSS系统中，由于没有能力提供足够的阻尼来维持稳定性，所以在故障排除后，发电机的转速一直处于波动状态。因此，图2所示的速度偏差在本质上是由CPSS(虚线)振荡引起的。对比ENABEC(虚线)的振荡更少，因为它可以提供更多的阻尼。但本文所设计的NABEC控制器(实线)比ENABEC控制器提供了更多的阻尼，使整个系统以更快的速度过渡到稳态。

图2 输入机械功率精确已知时G3的转速偏差

(2)发电机输入机械功率波动

当输入发电机的机械功率随着负荷波动，以满足不断变化的负载需求，同时系统中发生了三相短路故障。当故障恢复后，ENABEC控制方式将使发电机无法维持稳态运行状态。而本文提出的NABEC可以实时评估系统的运行状态，在故障恢复后保持稳定运行。通过图3所示G3同步发电机的转速偏差可以说明该控制策略的优越性。

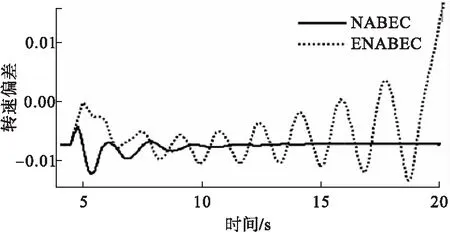
图3 输入机械功率未知时G3的转速偏差

6 结论

通过研究多机电力系统的暂态稳定问题，根据自适应理论框架，设计自适应非线性励磁控制器。参考李雅普诺夫函数的导数恒为负保证了所设计的自适应控制器下的多机电力系统的渐近稳定性，对系统的暂态稳定性进行了分析。仿真结果表明，与现有的控制器相比，所设计的控制器在相似框架下具有更快的收敛速度。仿真工作包括对所有敏感参数的发电机作为未知量进行考虑，并对不同运行条件下的多机电力系统进行动态稳定性分析。