基于智能电表数据的电池储能容量配置优化

钟晗炜，郑杰俊

(福州大学电气工程与自动化学院，福建 福州 350100)

1 引言

近些年来,随着我国经济和技术的高速发展，对能源产生了极大的需求，由于我国的经济增长方式仍然处于一种高投入、高排放、低效率的模式，这种模式造成了极大的资源浪费。目前，提高能源的使用效率，开发可再生能源，降低污染与温室气体排放，是世界各国都关注并积极探索的重要课题。电力作为最重要的二次能源，对能源高效利用和能源结构优化的格局转变有着重要意义。电池储能系统(Battery Energy Storage System,BESS)是提高电能使用效率的重要手段。在峰谷分时电价的背景下，用电用户可以通过谷电价时段对电池储能系统充电，并在峰电价时段对电池储能系统放电，以达到提高能源利用率的目的并节省用电用户的用电成本。

部署于用户侧的储能系统，其容量的大小极大地影响了电池储能系统的成本，若初期投资过高，用电用户或将无法承受。如果储能容量太大而无法在大多数时间内完全使用，则会造成投资上的浪费；另一方面，如果储能容量太低，不仅会因电池的过充、过放令使用寿命迅速减少，提高维护支出，还降低了使用电池储能系统所得到的收益。因此优化储能容量对于部署于用户侧的电池储能系统非常重要[1]。

现已进行许多研究工作对储能系统的容量大小进行优化。文献[2]针对峰值和负载减少问题建立了电池储能系统容量规划模型，并利用了两个不同优化目标的充放电功率的最优控制策略。如文献[3]建立了一个基于充放电功率和容量比较约束的储能容量优化模型，以最小化运行成本和建设成本之和。文献[4]考虑到电池储能系统容量优化及其经济效率和适应性，建立了峰值功率约束和综合成本效益模型。文献[5-7]提出了一种解决能量存储容量优化的智能算法，包括遗传算法和粒子群优化算法。文献[8]提出了与峰谷分时电价相关的电池储能系统最优运行策略，用以实现最大利润，结果表明储能装置的安装可以有效地节省能源成本。

本文的电池储能系统由储能电池、储能逆变器、智能电表、电气负载和电网组成。电池储能系统通过合适的充放电策略，电网的电经过储能逆变器对储能电池进行充电，储能电池对电气负载进行供电。本课题所研究的电池储能系统因未接入太阳能光伏发电等模块，故暂不考虑发电带来的影响。

但电池储能系统存在着储能容量配置不合理，导致容量浪费、引起成本过高致项目难落地等问题。

针对上述问题，本文将基于用智能电表所获取的福建某工业企业的用电数据，建立最优化数学模型，结合合适的充放电策略，采用遗传算法求解，对电池储能系统的容量进行优化配置。

2 用电数据的获取

本课题的研究对象是福建某工业企业，其电表计量功能单一，只能计量月总用电量等简单的用电数据，不能实时获取用电信息，且这些数据量级小精度差，在数据采集过程中，难以发挥作用。而目前的电表大多是老式电表，只能就地读取数据，不具备远程传输功能，所以仅能通过人工抄表的方式进行数据采集。为了满足对用电数据的分析，用电数据量应尽可能大，包含的月份和天数应尽可能多，且应具备实时性和正确性。故本课题在不影响原有的配电系统结构的基础上对该工业企业的电表进行了更换与升级，智能电表使用的是AEW100无线计量仪表和配套互感器。

该电表的作用是对三相有功功率进行采集，为用户实现在线监控、集中抄表、和用电数据管理提供有力帮助。采集精度高，能满足本课题的数据需求，体积小且安装方便，可以根据用户配电箱的具体情况灵活地装配，以完成对不同设备、不同楼层的分项电能计量。

本课题的研究对象在每层楼都安装了智能电表，以采集所有楼层的用电数据，从而进行分析。智能电表不仅支持电能计量，而且还能实现实时监控，用电数据存储和远程数据传输等功能。

3 用电数据说明

在工业企业的用电数据采集完成后，需要将这些数据应用到后续工作中。智能电表用电数据在本课题中相当于储能系统容量优化配置的基础。

本文的研究对象有三层楼，采集的智能电表数据是用户的原始数据，如表1所示，该表为该工业企业3楼2019年6月的部分数据，数据采集周期为1分钟。其中总有功功率单位为kW，正向有功用量单位为kW·h。

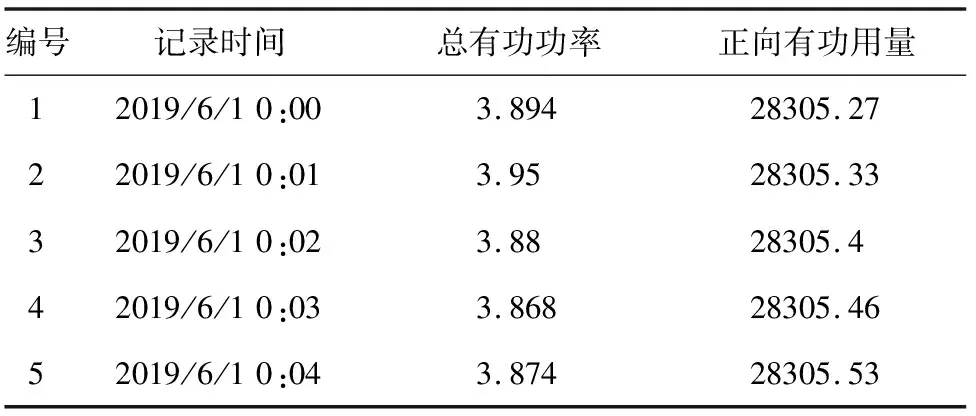
表1 2019年6月某工业企业3楼原始用电数据

考虑到后续要对储能容量进行优化配置，本文对三层楼的用电数据进行了整合，整合后的部分数据如表2所示。其中总有功功率单位为kW，总用电量单位为kW·h。为了后续的储能容量最优化，将三层楼的数据整合到了一起，并将采集周期取为30分钟。

表2 2019年6月某工业企业整合后用电数据

为了将用电数据应用到后续的储能容量优化当中，可以用基于用电数据的典型日负荷优化储能容量。

研究对象的电气负载包含了照明设备、计算机、工业设备测试台、空调和热水器等。这些电气负载具有显著的时变性，因不同的时段用户有各自的需求[8]。有许多方法可以获得典型日负荷，本文选用三种方法获取典型日负荷，分别是最大日负荷法、均值法以及K-Means法[9]：

(1)最大日负荷法，统计出用户用电数据中的最大值，取最大值所在的那一日作为典型日负荷。

(1)

式中，pa,b,c为第a月，第b日；第c时段的用电数据，n为总天数。

(3)K-Means法，K-Means法的做法是首先随机选取k个对象，并且每个对象最初代表一个簇的中心。对于其余每个对象，根据其与每个群集中心的距离将其分配给最近的簇，然后重新计算每个簇的平均值。重复该过程直到标准函数收敛。距离度量d为欧几里得距离。

d=(x-c)(x-c)′

(2)

式中，x为待聚类的相关因素构成的向量；c为最初指定的聚类中心的数量。

以最大日负荷法为例，以一天的48个时刻(即00:00、00:30、…、23:30)为横轴，求得的典型日负荷绘制成如图1所示。

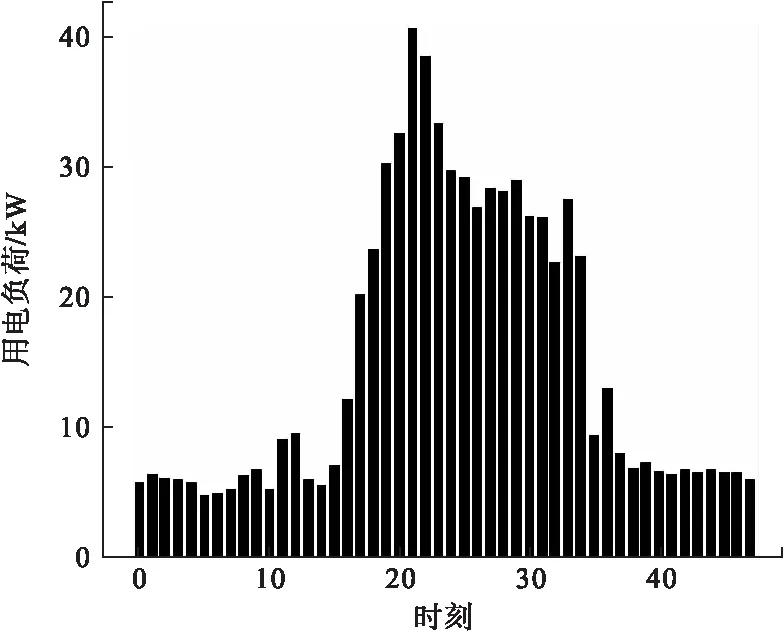
图1 典型日负荷

4 电池储能系统容量优化

为了降低电池储能系统的投资成本，并从中获取电价收益，对电池储能系统进行储能容量优化配置，以电池储能投资成本最低、获取最大收益为主要目标建立储能容量配置优化模型可以解决这一问题。

4.1 充放电策略

基于分时电价的充放电策略是在峰谷电价期间，用户通过电池储能系统调整充、放电，减少高价电力的购买。

本文基于图2所示的分时电价提出了一种简单的充电和放电策略。分时电价是指根据电力系统的运作将24小时分成各个部分，每部分的电价不同，包括峰时段、谷时段和平时段，以满足用户不同时段的用电需求。各个时段的电价皆是根据系统操作的平均边际成本来规定的。分时电价能很好地实现“削峰填谷”，并且能优化用电用户的用电方式[10]。

中国福建省的分时电价如图2所示。电价分为三个时段：

图2 各时段的分时电价

(1)峰时段：1.08 CNY/kW·h，时间段为8:30-11:30、14:30-17:30和19:00-21:00。

(2)平时段：0.72 CNY/kW·h，时间段为6:00-8:30、11:30-14:30、17:30-19:00和21:00-24:00。

(3)谷时段：0.36 CNY/kW·h，时间段为0:00-6:00。

如果电价处于谷时段，则用户将购买电力以对电池充电。如果电价处于峰时段，则电池储能系统将放电以降低高价电的使用。电池储能系统不在其他时期间充电或放电。

4.2 储能优化模型

根据如上所叙，在储能优化模型中应考虑电池储能系统投资成本、运维成本还有电价收益。储能优化数学模型应有目标函数与约束条件。

(1)电价收益

由图2给出的分时电价，将一天分为48个时段。根据文献[11]的研究工作和4.1章节的充放电策略，电价收益模型E可表述如下，

(3)

(2)电池储能系统的投资成本

本文电池储能系统的投资成本主要是储能电池的成本，本文选择使用磷酸铁锂电池作为储能介质。则电池储能系统的投资成本可表示为：

C1=rWKWW

(4)

其中，rW为储能系统的固定资产折旧率；KW为电池储能系统的单位造价；W为电池储能系统的最佳容量。

(3)电池储能系统的运维成本

为了保证装置正常运行，需定时进行装置的维护。电池储能系统的运维成本主要取决于自身的规模，则运维成本可以表示为C2：

C2=CmP

(5)

其中，Cm为单位容量的年运维成本；P为电池储能系统的最佳功率。

(4)电池储能系统的总收益

为了能最大化工业企业的应用储能设备的收益，并基于用电数据获得最佳容量W和最佳功率P，电池储能系统的总收益T可表示如下：

T=E-C1-C2

(6)

综上，本文建立的储能优化模型模型如下，

maxT=max(E-C1-C2)

(7)

(8)

(9)

(10)

(11)

Wups≤wj≤W

(12)

式(8)中的η为电池储能系统的充放电效率；w0表示的是电池储能系统的初始电量；Wups是不间断电源所需的容量，通常取为0.1倍的储能容量。

式(8)表示电池储能系统的充、放电约束，该系统必须保持每天的充放电平衡；式(9)和式(10)表示电池储能系统的功率约束；式(11)表示的是第j个时期开始时电池储能系统的电量wj；电池储能系统作为不间断电源(UPS)时，应该满足公式(12)给出的电量约束。

4.3 遗传算法流程

本文所述模型采用遗传算法结合可行性法则进行求解。遗传算法的步骤如下。

步骤1：读取电池储能系统的数据参数、分时电价与典型日负荷数据等。基于目标函数公式(7)、约束条件公式(8)至公式(12)和充放电策略，同时结合可行性法则，生成一个CV矩阵(种群个体违反约束程度矩阵)消除不等式约束条件，建立无约束条件的目标函数。

步骤2：设定遗传算法的种群规模、编码方式、最大进化代数等参数，创建区域描述器，设置的基本参数，并设置电池储能系统的最佳功率P和最佳容量W范围。

步骤3：计算种群中各个个体的适应度值，并评价各个个体。

步骤4：以一定的概率对种群个体进行交叉、变异等操作，产生新的个体。

步骤5：评价与选择新的个体，根据选择策略，从种群中选择个体进入下一代。

反复进行步骤4和步骤5，当满足终止条件时输出最优解算法结果；若不满足，则反复进行上述操作直至达到最大进化代数。

根据以上遗传算法步骤，对储能优化模型进行求解。

5 算例分析

本文算法采用PYTHON语言编程进行求解。研究对象是某福建工业企业，使用智能电表对该企业三层楼的用电数据进行实时采集和存储，采集周期为2019年1月到2019年12月，取2019年4月到6月的智能电表数据作为本课题研究的原始数据。通过上述介绍的遗传算法与可行性法则，采用上述的充放电策略，对储能系统的容量配置最优化问题进行求解。数据参数包含三种：以最大日负荷法、均值法与K-Means法得到的典型日负荷。基于上述典型日负荷，以磷酸铁锂电池为配置对象，通过对磷酸铁锂电池的了解和数据收集，得储能系统装置的参数如下：固定资产折旧率rW=0.09，BESS的单位造价KW=1500CNY/kW·h，BESS的储能效率η=0.94，单位容量的年运维成本为Cm=20CNY/kW。

根据前述章节的内容求解，其优化结果如表3所示。

表3 各类典型日负荷的优化结果

由表3可看出，最大日负荷法的最佳功率和最佳容量分别为14.64kW和71.33kW·h(实际应用可近似取为14kW和72kW·h)。在安装本装置前，该工业企业三个月的初始电费为13214.47元，安装储能装置并通过储能优化后，电费可降至9285.49元。电价收益为3928.98 元，考虑投资和维护成本后总收益为1448.27元。

对比使用均值法和K-Means法求解的典型日负荷，优化后的总收益均不如最大日负荷法，K-Means法所求结果比均值法稍好。由上分析可以得知，最大日负荷法为最佳方法，使用最大日负荷法可得到更多的收益。

6 结论

本文基于智能电表收集的工业企业用电数据，使用多种方法得到典型日负荷，通过建立储能优化模型，在峰谷分时电价的背景下，设置合适的充放电策略，最终选择使用遗传算法结合可行性法则求解电池储能系统的容量优化问题。本文以电池储能系统的总收益为最大化目标，求解的同时获得最佳容量和最佳功率。最后，对算例的计算分析来验证了所提出的储能容量优化模型的有效性，实现工业企业用电成本降低，提高其能源利用率，为其扩大生产奠定基础。