基于空间邻近点与极限学习机的大坝位移缺失数据补齐

邱德俊，周 洋，仲静文，贾玉豪

(1.南京市水利规划设计院股份有限公司，江苏 南京 210022;2.河海大学水利水电学院，江苏 南京 210098；3.上海勘测设计研究院有限公司，上海 200335)

0 引 言

借助先进的数学模型，利用大坝长时期服役过程中产生的位移监测数据，对大坝安全性态开展研究一直是大坝安全监控领域的重点研究方向[1-3]。然而，在大坝长期服役过程中不可避免地会出现位移监测数据缺失的情况，不利于大坝监测数据的分析处理[4-5]。因此，研究大坝位移监测缺失数据的补齐方法尤为重要。以往补齐大坝位移缺失数据多采用传统的插值估计法。吕开云[6]指出观测数据插补的方法主要包括内在物理联系插补法和数学插补法，介绍了线性插补法的原理和过程；李双平等[7]对比了常用的数学插值方法，并选择了充分利用已有数据信息、插值曲线光滑的三次Hermite分段插值。但这类方法仅基于已知数据，没有结合大坝的长效服役特点。由大坝变形统计模型理论可知，大坝变形主要受水位、温度和时效3个分量的影响。为此，有学者提出将水位、温度和时效作为大坝变形的影响因子，借助BP神经网络映射方法对位移缺失数据进行补齐。然而，仅考虑大坝变形统计模型分量并不能合理地估计出缺失数据，同时BP神经网络算法容易陷入局部最优、收敛速度较慢的情况。由于大坝变形具有良好的整体性和连贯性，因此大坝局部区域的变形在一定程度上具有相关性，同一监测项目的一系列测点在变形上具有高度的相似性，可以融合相关测点的监测信息对目标测点进行插值[8-10]。

本文利用目标测点的空间邻近点变形值与统计模型中的分量(水位、温度和时效)作为影响因子来估计目标测点的缺失数据。为全面刻画出各测点变形之间的未知作用关系，本文引入了极限学习机算法，极限学习机(Extreme Learning Machine，ELM)是由Huang等[11]提出的一种单隐层前馈神经网络算法，其可随机选择输入权值和确定输出权值。与BP神经网络等算法相比，ELM运算速度更快，全局最优解预测精度更高。本文基于空间临近点和极限学习机算法，对大坝位移监测缺失数据进行补齐，并结合大坝工程实例进行方法合理性的有效检验。

1 极限学习机基本原理

给定一个包含N组大坝监测数据的样本集R(xi,ti)，其中ti=[ti1,ti2,…,tim]T∈Rm,ti=[ti1,ti2,…,tim]T∈Rm,则一个具有M个隐含层节点以及激励函数g(x)的极限学习机形式[12]为

(1)

(2)

(3)

(4)

2 考虑空间临近点的缺失数据补齐方法

2.1 相邻测点的影响因子

假设某混凝土坝局部区域3个位移测点的位置相近，分别是测点A、B、C，如图1所示，其中测点A和测点C的位移监测数据序列完整，测点B的部分监测数据缺失。考虑到大坝的整体性和连贯性，测点B的变形值与测点A和测点C的变形值之间存在一定的相关关系，因此可将测点A和测点C的变形值作为训练和补齐B点位移的影响因子。

图1 混凝土坝局部区域测点变形示意

2.2 荷载的影响因子

由大坝变形的统计模型可知，变形主要由水压分量δH、温度分量δT和时效分量δθ组成，即δ=δH+δT+δθ，因此可将水位、温度和时效作为训练和补齐测点B位移的另一部分影响因子。

综上所述，对目标测点B的缺失数据补齐时，首先应将上述两部分影响因子同时作为极限学习机的输入项，将测点B相应的位移作为输出项，进而训练得到影响因子与位移的拟合关系；最后通过训练得到的拟合关系，输入缺失值对应的影响因子则可得到拟合的缺失值。

通常使用平均绝对误差(Mean Absolute Error，MAE)、平均相对误差(Mean Relative Error，MRE)、均方误差(Mean Square Error，MSE)对缺失数据补齐后的结果进行合理性评价，计算式分别为

(5)

(6)

(7)

式中，yD(i)表示大坝位移补齐值；y(i)表示大坝位移实际值；n为缺失样本总数。

3 工程实例

某水电站位于我国沿海地区，大坝主体为碾压混凝土重力坝，最大坝高72.4 m，坝顶高程634.40 m，坝顶全长206 m，水库总库容4 700万m3。选取该坝6号坝段上的顺河向水平位移的监测数据序列，共有132测值，人为构造出一个32个测值数据缺失段，对该位移缺失数据段进行补齐。其相邻测点的水平位移监测数据、坝体温度和库水位观测数据如图2所示。

图2 某碾压混凝土重力坝监测数据

为了进行成果对比，分别采用下列3组方案进行位移缺失数据补齐：

(1)方案1。基于极限学习机算法，选取目标测点的空间临近点位移测值和大坝变形统计模型分量(水位、温度和时效)作为影响因子，对大坝位移缺失数据进行补齐，该方案为本文推荐方法。

(2)方案2。基于BP神经网络算法，影响因子的选取和方案1相同。

(3)方案3。基于极限学习机算法，仅选取大坝变形统计模型分量(水位、温度和时效)作为影响因子。

图3为各方案位移缺失数据补齐结果对比。由图3可知，方案1的拟合效果较好，拟合精度更高。对比上述3种方案的评价指标(MAE、MRE、MSE)，如表1所示。通过对比各评价值结果，再次验证了方案1的有效性。由表1可知，方案1的各类评价指标值均小于另外2种方案，说明方案1的补齐数据与实测数据的相似度最高，误差最小。

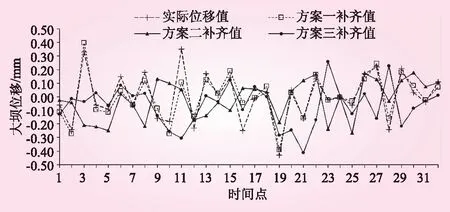
图3 各方案位移缺失数据补齐值对比

表1 各方案评价指标值

4 结 论

(1)对于大坝位移缺失数据补齐，将目标测点的空间邻近点测值和统计模型中的分量同时作为影响因子比仅将统计模型中的分量作为影响因子的效果更好，准确度更高。

(2)工程实例证明，在选择相同影响因子的条件下，基于极限学习机算法的缺失数据补齐方法比基于BP神经网络算法的缺失数据补齐方法准确率更高，更适用于大坝位移缺失数据补齐。

(3)大坝位移缺失数据受到多维度因素的影响，运用先进的数学、力学工具对大坝位移缺失数据的影响因子进行多角度深入挖掘，是未来研究的重点方向。