基于差分原理的喷锚支护水工隧洞稳定可靠度分析

方苗苗，李梦瑶，王 刚，崔鹏飞

(大连理工大学水利工程学院，辽宁 大连 116024)

0 引 言

目前，我国水工隧洞的建设水平不断取得突破，建设规模向大埋深、长距离、大断面趋势发展，如锦屏二级水电站引水隧洞埋深达2 525 m，开挖洞径达14.6 m[1]。随着隧洞建设规模的增大，其稳定安全问题也愈发突出，其中隧洞围岩与支护的整体稳定问题是隧洞设计关注的重点。在水工隧洞的建设中，采用喷锚支护和先喷锚后二次衬砌的水工隧洞较为常见，如蒲石河抽水蓄能电站地下厂房洞室用喷锚支护做永久支护[2]，九甸峡水利枢纽工程引水发电洞用喷锚支护做一次支护[3]等。隧洞喷锚支护后(或二次衬砌前)围岩与喷锚支护的整体失稳时有发生，常造成围岩变形坍塌和二次衬砌破坏等事故[4]。因此，研究喷锚支护水工隧洞围岩与喷锚支护联合承载时的稳定可靠性意义重大，亟待采用可靠度方法研究解决。

当前，结构可靠度计算的常用算法有蒙特卡洛法和二阶矩法(即验算点法，如一次二阶矩法、二次二阶矩法等)。蒙特卡洛(MC)法包括直接抽样、重要抽样等算法。其中MC直接抽样法(MC-DS)对大型复杂结构系统的可靠度计算适用性强，保证抽样次数的条件下，计算结果相对精确，一般作为其他算法的校准算法；由于MC-DS计算量大、效率低，通常需要进行算法改进，如改变其抽样中心的MC重要抽样法(MC-IS)，此改进方法先通过一次二阶矩法求出验算点，然后以验算点为抽样中心进行下一步抽样计算，从而提高计算效率。而一次二阶矩法(FOSM)、二次二阶矩法(SORM)等需求解验算点的可靠度算法通常需要功能函数为显式，然后将功能函数在验算点处泰勒展开，并近似取至一次项或二次项，以便求得功能函数近似的一阶或二阶偏导数，因此二阶矩法计算精度一般低于MC法，但效率较高。

本文以圆形断面水工隧洞为例，对喷锚支护隧洞进行围岩与支护结构稳定可靠度计算方法研究。首先，基于岩体理想弹塑性本构模型推导出隧洞可靠度计算所需的功能函数，由于此功能函数是非线性隐式的，传统FOSM和SORM方法难以直接运用，本文将采用差分理论予以解决；然后，结合水工隧洞工程实例，分别采用基于差分原理的FOSM、SORM和MC-DS、MC-IS进行隧洞围岩与喷锚支护结构的稳定可靠度计算，并进行不同方法的对比分析。本文研究成果可为水工喷锚支护隧洞的安全可靠性分析和评价提供理论和方法参考。

1 喷锚支护隧洞可靠度计算功能函数

1.1 最小围岩压力

在轴对称条件(λ=1，λ为侧压力系数)下估算最小围岩压力Pa，min，条件是维持松动区滑移体平衡所需的支护阻力等于保持极限平衡状态的力。根据剪切滑移理论[5]，可得

Pa,min=γRmax-γr0

(1)

式中，Pa，min为最小围岩压力；Rmax为与Pa，min相对应的最大的松动区半径；γ为围岩的容重；r0为开挖半径。

根据隧洞围岩应力和位移的弹塑性分析[6]，松动区最大半径Rmax为

(2)

式中，c、φ分别为锚固后的围岩黏聚力、内摩擦角。

锚固后的围岩黏聚力、内摩擦角c、φ分别为

(3)

式中，τa、As、Sa、Sb分别为锚杆的抗剪强度、横断面积及横、纵间距；σz为围岩的初始应力(侧压力系数λ=1)；c0、φ0分别为围岩黏聚力、内摩擦角。

将式(2)代入式(1)可求得最小围岩压力Pa，min，即

(4)

1.2 喷射混凝土支护阻力

对喷射混凝土提供的支护阻力作简化考虑[7]，即

(5)

Pa=-ccotφ+(1-sinφ)(ccotφ+σz)

(6)

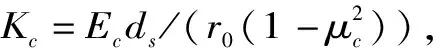
(7)

当厚度ds>0.04r0时，根据厚壁圆筒理论，支护阻力与结构刚度的关系为

(8)

1.3 锚杆支护阻力

采用常用的点锚式锚杆，按照锚杆与围岩共同变形理论，得锚杆支护阻力Pi为[7]

(9)

(10)

联立式(9)和(10)，可最终求得锚杆支护阻力Pi。

1.4 隧洞围岩喷锚支护结构功能函数

当围岩所需最小支护阻力与喷锚支护所提供的支护力间达到平衡时[8]，即当等于Pa与Pi之和时，为结构的极限平衡状态，由此可建立可靠性分析所需功能函数

g(X)=Pa+Pi-Pa,min

(11)

综合观察式(1)～(11)中的Pa、Pi、Pa，min可以看出，功能函数g(X)是关于c和φ的隐式非线性函数，不能直接采用常规二阶矩法进行可靠度计算。

2 基于差分原理的可靠度研究方法

2.1 功能函数偏导数的计算

FOSM与SORM在计算各随机变量X=(X1，X2，…，Xn)的偏导数时，需要显式的功能函数Z=g(X)，而在实际工程中若遇到功能函数是隐式的情况，可根据差分原理[9]求得验算点X0处功能函数对各变量的偏导数为

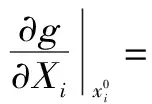
(12)

(13)

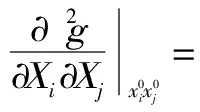
(14)

式中，α为步长系数，为使偏导数计算有更高的精度，α取值应尽量小。

2.2 基于差分原理的一次二阶矩法和二次二阶矩法

在FOSM的计算过程中，利用式(12)求出功能函数在验算点处的一阶偏导数；在SORM的计算过程中，先需要用FOSM求出验算点，再利用式(13)和式(14)计算在验算点处的二阶偏导数。

2.3 蒙特卡洛重要抽样法

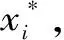
(15)

若X1与X2具有相关性，用式(16)计算X1与X2的联合概率密度函数

(16)

3 工程实例

某隧洞断面形式为圆形，开挖半径5.4 m，隧洞埋深在200 m左右。穿越地段围岩分类为III类。采用新奥法设计施工，初期支护为喷锚支护方式，如图1所示。

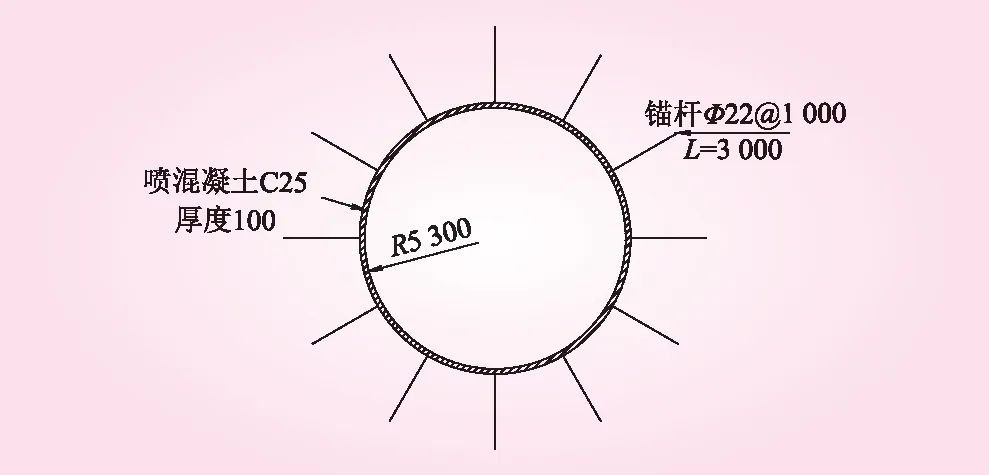
图1 隧洞喷锚支护示意(单位：mm)

表1 各随机变量统计特征

3.1 差分计算步长系数的确定

采用MC-DS计算100万次得到的可靠指标β为3.229 1，失效概率pf为6.21×10-4，根据GB 50199—2013《水利水电工程结构可靠度设计统一标准》[10]可知该水工隧洞围岩是稳定的。基于差分原理计算可靠度时，步长系数的取值影响可靠度的精度，故计算不同步长系数下的可靠度，结果如表2所示，从而确定合适的步长系数取值。

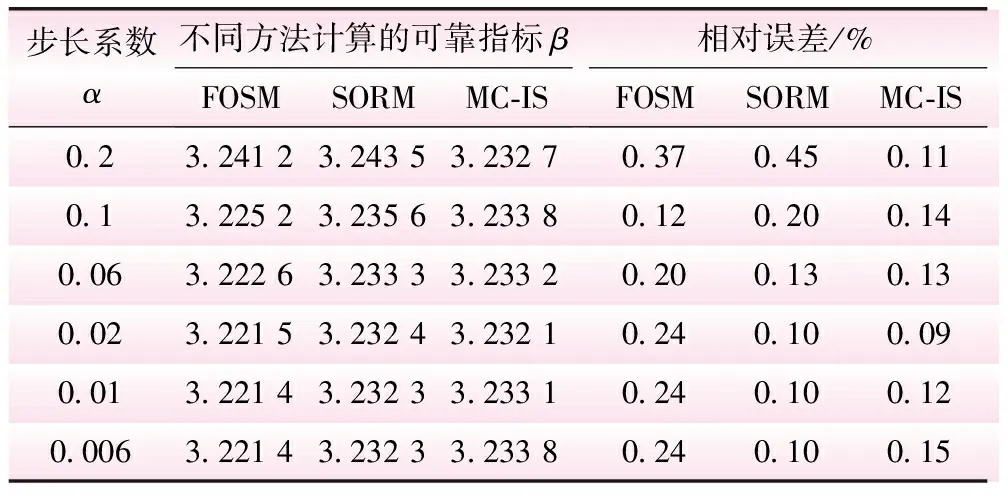
表2 不同步长系数下可靠度的计算结果

由表2可知，当步长系数α<0.02时，用FOSM和SORM计算的可靠指标β趋于稳定。当α=0.01时，迭代次数为8次，比MC法效率高，此时FOSM和SORM计算结果的相对误差分别为0.24%和0.10%。SORM比FOSM的精度高，与MC法计算精度相当，这是由于FOSM没有考虑功能函数在设计验算点附近的局部性质，而SORM通过计算功能函数的二阶导数考虑了极限状态曲面在验算点附近的凹向、曲率等非线性性质，提高了精度。

MC-IS的计算结果与步长系数α基本无关，为便于计算效率对比分析，取α=0.01进行MC-IS计算，抽样10万次的可靠指标β为3.232 9，相对误差为0.12%，精度高，大大提高了抽样效率，这是由于MC-IS是以FOSM求出的验算点为抽样中心，使样本点有较多机会落进失效域，增加功能函数Z<0 的机会。

3.2 考虑随机变量统计特征的隧洞可靠度分析

在水工隧洞围岩稳定分析中，黏聚力c和内摩擦角φ的分布类型不确定，一般为正态分布或对数正态分布。本文对c和φ分别为正态分布和对数正态分布时的可靠度进行计算，结果如表3所示。由表3可知，c为对数正态分布时，可靠指标变化不大，φ分布类型对可靠指标的影响较大，而φ为对数正态分布时，可靠指标变小，故针对c、φ均为正态的情况进行研究。

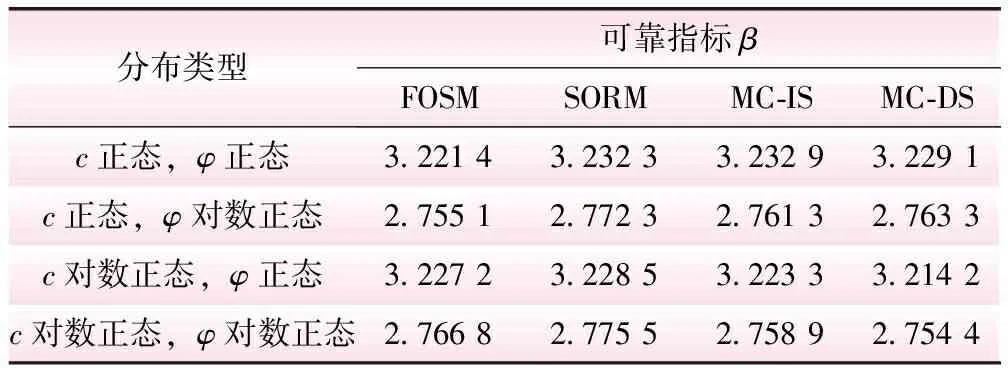
表3 不同分布类型下可靠度的计算结果

实际上，c，φ一般具有负相关性，对c、φ相关系数不同时的可靠度进行计算，结果如表4所示。由表4可知，β随c和φ的负相关性的增大而增大，这与已有研究的结论是一致的。

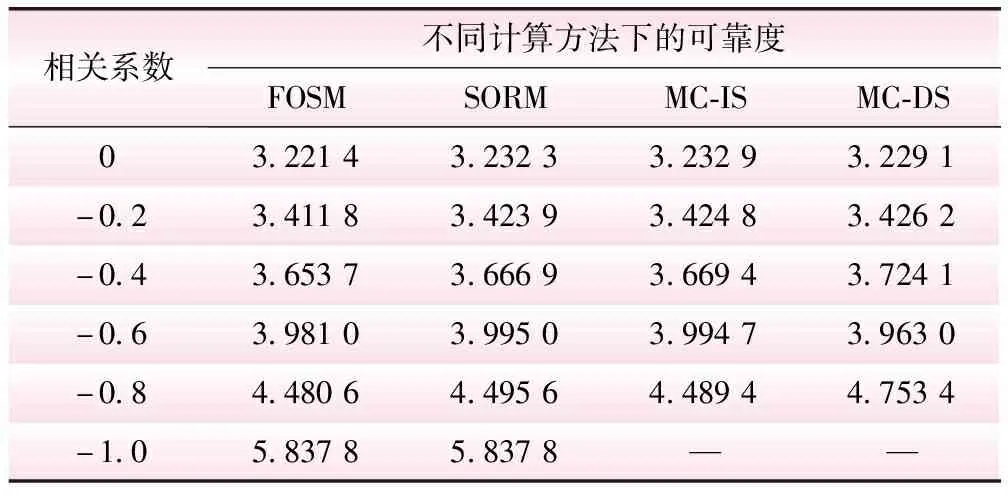
表4 随机变量相关时可靠度的计算结果

4 结 论

本文提出了基于差分原理的一次二阶矩(FOSM)和二次二阶矩(SORM)可靠度算法，并对喷锚支护圆形隧洞围岩与支护系统稳定可靠度进行计算分析，得到如下研究结论：

(1)基于差分原理的FOSM和SORM验算点法能很好地处理功能函数是非线性隐式的情况。

(2)结合工程实例对差分步长进行了研究，得到了不同步长系数下喷锚支护隧洞稳定可靠度的计算结果，基于差分原理的FOSM和SORM法在步长小于0.02的情况下可靠度计算结果趋于稳定。

(3)通过与蒙特卡洛直接抽样法(MC-DS)和重要抽样法(MC-IS)对比分析可知，基于差分原理的FOSM和SORM法计算结果精确且高效，能够满足实际工程计算要求。

(4)工程实例可靠度研究表明，围岩抗剪强度参数c和φ的分布类型不同，得到的可靠指标也不同，c分布类型变化对可靠指标影响不大，而φ分布类型为对数正态分布时，可靠指标较正态分布时小，c、φ的负相关性对隧洞围岩稳定可靠指标影响显著，随着负相关性的增强而增大，这与已有研究的结论一致，表明本文方法具有很好的适用性。