Radiation force and torque on a two-dimensional circular cross-section of a non-viscous eccentric layered compressible cylinder in acoustical standing waves

F G Mitri

Santa Fe,NM 87508,USA

Keywords: radiation force,radiation torque,liquid compound cylinder,multiple scattering,acoustical standing waves

1. Introduction

Acoustical standing (or stationary) waves provide efficient means of particle entrapment and immobilization in acoustical tweezers applications, ever since the pioneering work[1]demonstrated that micron-sized latex beads and clusters of frog eggs can be trapped,moved and translated axially or laterally. Other geometries have been considered, and experiments dealing with the alignment of cylindrical elongated particles in acoustic standing waves have been also reported,such as carbon nanotubes[2,3]and fibers.[4–6]In the context of acoustofluidics applications,surface acoustic waves have been utilized[7]where standing waves enabled cell focusing and liquid droplet sorting and patterning.

For experimental design purposes and instrumentation optimization, analyses have relied on theoretical formalisms for the time-averaged radiation force for cylindrical rigid,[8–11]fluid,[12]elastic,[12–16]and viscoelastic materials.[12,17,18]The effects of the host medium viscosity have been also considered,[19]and further generalizations taking into consideration the profile of the incident wavefront (unlike plane waves)[20,21]and particle shape[22–24]have been examined. Numerical computations for the radiation force of non-paraxial[25–28]wavefronts showed interesting capabilities from the standpoint of particle attraction, as well as linear,parabolic and reverse cylindrical particle movement dynamics.Although other analyses attempted to evaluate the acoustic radiation force on a circular cylindrical particle[29,30]in the field of a standing surface acoustic wave(SSAW),the reader is cautioned that the effect of the micro-channel bottom boundary was neglected in those studies. Earlier radiation force results for a(spherical)particle near a flat(porous)surface[31]demonstrated that significant changes leading to attraction,neutrality or repulsion emerge as a consequence of the multiple scattering and wave interference effects occurring between the particle and boundary/edge, which cannot be ignored. Other related contemporaneous researches[32–34]investigated such effects for a rigid[32]and liquid[34]cylindrical particle near a flat boundary[32,34]and a rigid(90◦)corner-space.[33]

A particular particle geometry is the eccentric compound cylinder (Fig.1), composed of an inner cylindrical core (of radius b), coated by another cylinder of larger radius a>b.In this configuration, the two cylinders are not necessarily concentric, and the distance d determines the eccentricity.With the increase of the eccentricity (i.e., d >0), the acoustical scattering by the compound cylinder can be enhanced or reduced;[35–37]specifically, branching and a shift in resonances occur,which amount to the degree of eccentricity.[38,39]

Fig.1. Description for the acoustical interaction of standing waves (having an arbitrary angle of incidence α)with a compound non-viscous liquidcoated cylinder. The rotating arrow designates the axial torque component about the center of the compound cylinder of radius a,coating the one with radius b,while the distance d from the center denotes the eccentricity.

An important question that arises from the standpoint of linear and angular acoustic momenta transfer theory and applications in trapping and immobilization using acoustical standing wave tweezers,is how eccentricity affects the acoustic radiation force and torque exerted on a compound layered cylindrical particle properties in acoustical standing waves as d >0? The purpose of this analysis is to address this question. Although the scientific literature is abundant with numerous radiation force studies, the previously developed formalisms are not applicable for the eccentric compound cylinder in acoustical standing waves, although a recent analysis has addressed the case of plane progressive waves.[40]It is therefore of some importance to devise a formalism to take into consideration the geometrical asymmetry and the emergent phenomena that arise from it. Particularly,in the present investigation, it is demonstrated that in addition to the radiation force phenomenon due to linear acoustic momentum transfer,a time-averaged(quadratic)radiation torque(causing particle rotation due to angular momentum transfer)occurs.In contrast with the results of a previous study,[25]the radiation torque is not associated with sound absorption as the eccentric fluid layered cylinder considered here is non-viscous. Rather,it emerges because of geometrical asymmetry with respect to the axis of the compound cylindrical particle of radius a. This effect cannot be overlooked and must be estimated in experimental design and optimization analyses.

2. Theoretical analysis

The analysis assumes an acoustical standing wave field in a lossless unbounded host fluid medium(assuming linear wave motion),interacting with an eccentric compound cylinder with inner core and outer layer liquid media as shown in Fig.1. As such,the effects of viscosity of the host liquid medium of wave propagation, acoustic streaming as well as surface tension at the liquid–liquid interfaces are not considered. The wave-field is composed of equi-amplitude plane standing waves with an arbitrary angle α in the polar plane with respect to the center. The incident field is expressed in a Cartesian system of coordinates(x,y,z)by its velocity potential,

where ϕ0is the amplitude,k(=ω/c)is the wavenumber in the medium of wave propagation,ω is the angular frequency,c is the speed of sound for the compressional wave,and h is the distance from the center of the cylinder to the source.

Equation (1) is expressed using a partial-wave series expansion in cylindrical coordinates, since the modal expansion method[41]provides adequate means to evaluate the scattering and other physical observables. Therefore, using the Jacobi–Anger expression,[42]the series-expansion of Eq.(1)is written as,

where Jn(·)is the cylindrical Bessel function of the first kind.

In the lossless medium of wave propagation,the scattered velocity potential field is expressed as,

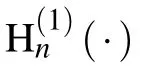
Denoting the internal non-viscous fluid-like cylindrical media composing the layer and core by medium 1 and medium 2,respectively,the corresponding scalar velocity potential fields are determined,respectively,as,

leads to the mathematical expressions for the longitudinal and transverse dimensionless components as

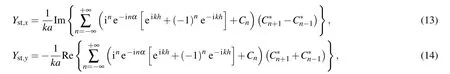
where the symbol Im{···}represents the imaginary part of a complex number.

Similarly,the acoustic radiation torque vector is calculated based on the far-field scattering as,[46]

Algebraic manipulation of the integral given by Eq.(16)using Eqs.(B2)–(B4)in Appendix B provides the exact equation for the axial component of the radiation torque vector in plane standing waves with arbitrary incidence,as

3. Computational results

The main results of this work are presented in Eqs. (13), (14), and (18) for the dimensionless longitudinal and transverse components of the radiation force vector as well as the axial component of the radiation torque vector. Clearly,these functions(or efficiencies) depend on the weighted coefficients Cnof the compound eccentric cylinder, coupled to those of the incident plane standing wave field. For accurate computational purposes, the partial-wave series equations are truncated at a maximum integer limit Nmax=round[ka+4.05(ka)1/3+12](exceeding ka)to warrant convergence.[47]

Those series given by Eqs. (13), (14), and (18) and implemented in a MATLAB program code, are computed for a nonviscous liquid-filled eccentric cylinder submerged in water(ρ =1000 kg/m3, c=1500 m/s), and made of a high-density liquid,such as mercury (ρ1=13600 kg/m3, c1=1407 m/s), with its core cylindrical medium made of water (ρ2=ρ, c2=c) or air(ρ2=1.23 kg/m3, c2=340 m/s). Initially, the dimensionless size parameters for the inner cylinder kb and eccentricity kd have taken different fixed values to illustrate the analysis. To ensure the physicality of the computations, the calculations have been performed in the ranges determined by(kb+kd)＜ka ≤5+(kb+kd),and 0 ≤α ≤180◦. In other words,the condition a>(b+d)has been enforced throughout the computations such that the cylinder core cannot be external to the layer medium to warrant analytical continuation.In the simulations,the distance parameter h is chosen conveniently to depend on the wavenumber k such that h=π/(4k).

Panels(a)and(b)of Fig.2 display the two-dimensional(2D)plots versus(ka,α)for the longitudinal and transverse radiation force functions, respectively. The inner core cylindrical material is composed of water while the outer layer is made of liquid mercury. For improved visualization and interpretation of the results,the solid(black)contour line is displayed,which indicates the neutrality of the longitudinal and transverse radiation force efficiencies (i.e.,Yst,x=0;Yst,y=0). In this configuration, the inner fluid cylinder is located at the center of the large cylinder such that kd=0, and kb=0.1, corresponding to a small core.This configuration corresponds to a concentric(i.e.,kd=0)cylindrical shell,such that an asymmetry in panel(a)and symmetry in panel (b) with respect to the incidence angle value α =90◦arise. Panel (c) displays the plot for the axial component of the radiation torque function that vanishes as required by the concentric geometrical symmetry regardless of the value of α.Another quadratic physical quantity of interest is the extinction (or scattering) energy efficiency, which is computed using the expression[48]

The related computational plot shown in panel(d)displays a complete symmetry versus the incidence angle value α=90◦,which clearly verifies the accuracy of the results based on energy conservation and the reciprocity theorem.[49]Based on Eq.(19),the absorption energy efficiency[48,50]Qabs=Qext−Qscais zero for a lossless concentric fluid-like cylinder.

Fig.2. Panels(a)–(d)display the 2D plots versus(ka,α)of the dimensionless efficiencies Yst,x,Yst,y,τst,z,and Qext,respectively,for kd=0 and kb=0.1.The inner cylindrical core is composed of water,while the layer is made of mercury.

In order to break the geometrical symmetry, the eccentricity is increased such that kd =2 and kb=0.1, and the inner core cylindrical material is composed of water while the outer layer is made of liquid mercury. The increase of the eccentricity induces variations in the radiation force,torque and extinction/scattering efficiencies,as shown in panels(a)–(d)of Fig.3,which are quite distinct from those displayed in panels (a)–(d) of Fig.2. The plot in panel (a) shows that Yst,xalternates between positive,negative,and neutral(i.e.,solid black line)values as(ka,α)increase. Similar sign changes are also noticed in panel(b)for Yst,yand panel(c)for τst,z. Without a doubt, the eccentricity/asymmetry(i.e., kd/=0)leads to the rise of an axial radiation torque component,which takes positive,negative,or neutral values along the solid(black)contour lines that surround the regions of positive and negative values. The sign changes (i.e., positive to negative) indicate that depending on the values of (ka,α),counter-clockwise rotation in the polar plane,or clockwise rotation about the center of the cylinder of radius a occur due to the transfer of angular momentum. Neutrality (i.e., τst,z=0) along the solid (black) lines also indicates no rotation. The plot in panel(d)of Fig.3 shows that Qextis always positive,in complete agreement with the law of energy conservation.

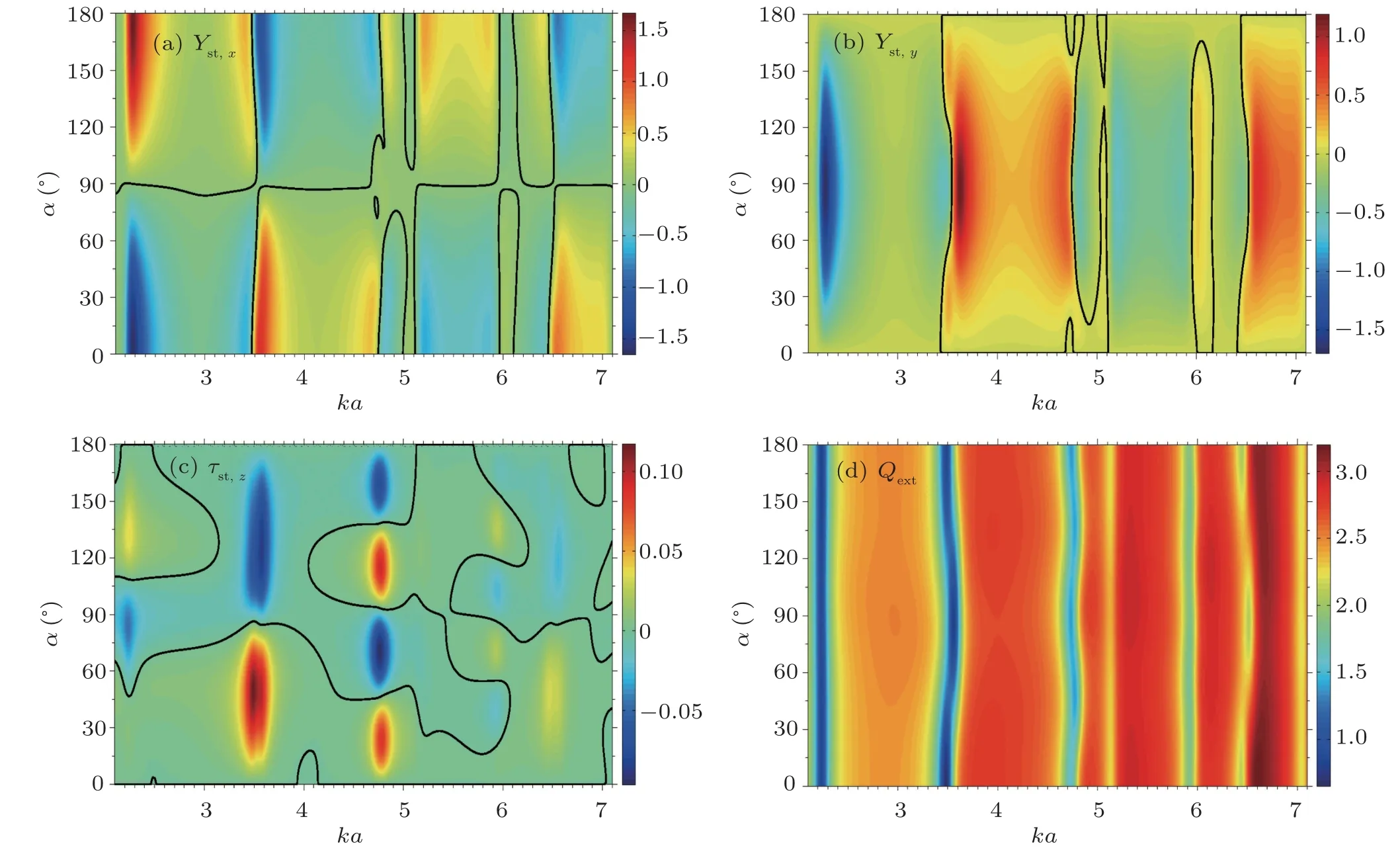
Fig.3. Panels(a)–(d)display the 2D plots versus(ka,α)of the dimensionless efficiencies Yst,x,Yst,y,τst,z,and Qext,respectively,for kd=2 and kb=0.1. The inner cylindrical core is composed of water,while the layer is made of mercury.

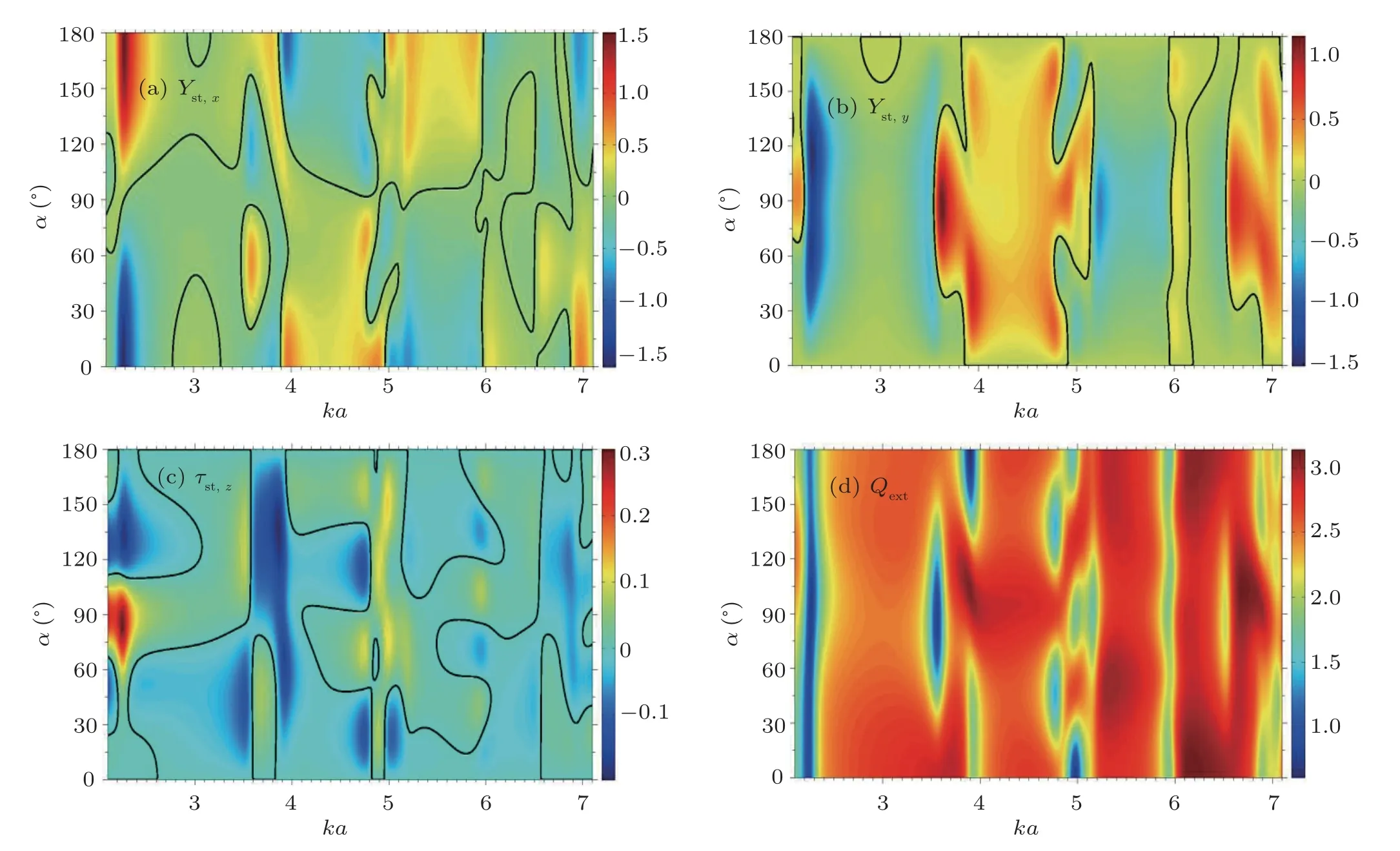
Fig.4. Panels(a)–(d)display the 2D plots versus(ka,α)of the dimensionless efficiencies Yst,x,Yst,y,τst,z,and Qext,respectively,for kd=2 kb=0.1. The inner cylindrical core is composed of air,while the layer is made of mercury.

The effect of changing the physical/mechanical properties of the inner core material has been also investigated,by choosing an inner air cylindrical bubble cylinder layered by a compressible mercury cylinder. Similarly to Fig.3, the eccentricity is set to kd=2 while kb=0.1. Comparisons of the plots in panels(a)–(c)of Fig.4 with those of Fig.3 show that the axial radiation torque function increases (in absolute sense) while the longitudinal and transverse radiation force efficiencies are comparable.The extinction energy efficiency displayed in panel(d)of Fig.4 exhibits different variations,which indicates that the changes in the physical properties of the inner core strongly enhance or reduce the energy efficiency as(ka,α)vary.

The effect of increasing the inner cylinder radius is examined by choosing kb=2, while keeping kd (=2) constant and the inner core cylindrical material is composed of water while the outer layer is made of liquid mercury. The corresponding computational plots are shown in panels(a)–(d)of Fig.5. As shown in all the panels,the asymmetry versus the incidence angle α =90◦increases as the ka increases. The plots for the dimensionless functions Yst,xand Yst,yalternate between positive or negative values while crossing zero as the α varies. The plot in the panel(c)of Fig.5 shows more intricate characteristics than its counterpart of the panel(c)of Fig.4,where the solid(black)lines demarcate regions/islands over which a negative radiation torque efficiency arises;τst,z＜0. Moreover,the panel(d)shows that extinction/scattering increases as ka and kb increase,such that the property of Qext>0 is always preserved,which verifies the results from the standpoint of the energy conservation applied to scattering.

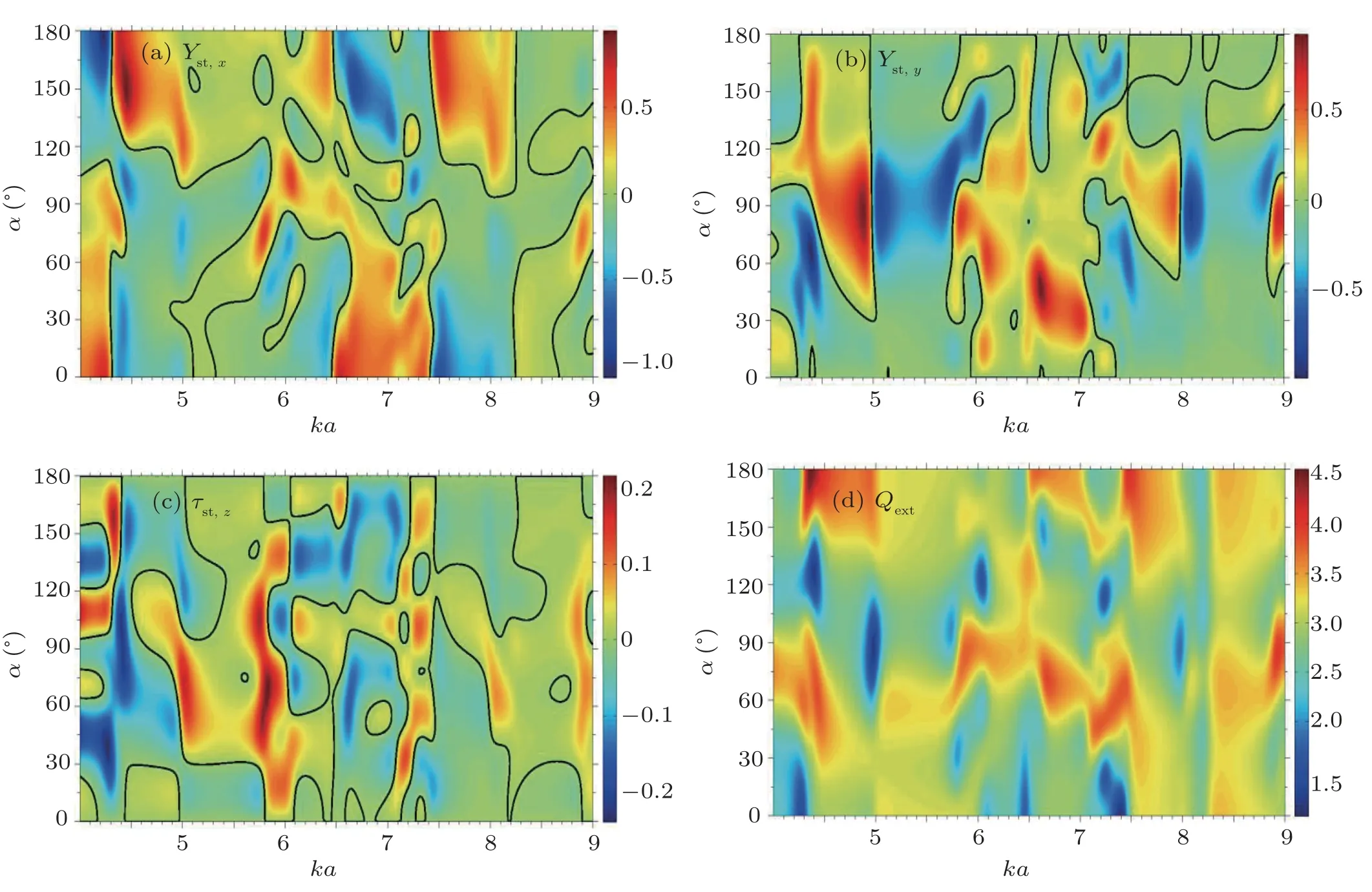
Fig.5. Panels(a)–(d)display the 2D plots versus(ka,α)of the dimensionless efficiencies Yst,x,Yst,y,τst,z,and Qext,respectively,for kd=2 and kb=2. The inner cylindrical core is composed of water,while the layer is made of mercury.

Additional computations have been performed to investigate the variations of the radiation force, torque, and extinction/scattering energy efficiency versus(α,kd)for fixed values of ka and kb.

The corresponding results are displayed in panels (a)–(d) of Fig.6 for ka=5 and kb=0.1, while the panels in Fig.7 correspond to a larger core liquid cylinder with kb=2, while ka (=5) is kept constant. Clearly, as the eccentricity increases,positive,negative,and neutral radiation force and torque components are predicted,while the extinction energy efficiency remains positive,in agreement with the law of energy conservation applied to scattering. For a fixed value of the incidence angle α and as kd varies,the physical observables change sign. Alternatively,for a fixed value of eccentricity kd while α varies,the sign is also altered. Moreover,as kb increases,an increase in amplitude is perceived for all the physical observables.

Fig.6. Panels(a)–(d)display the 2D plots versus(kd,α)of the dimensionless efficiencies Yst,x,Yst,y,τst,z,and Qext,respectively,for ka=5 and kb=0.1. The inner cylindrical core is composed of water,while the layer is made of mercury.

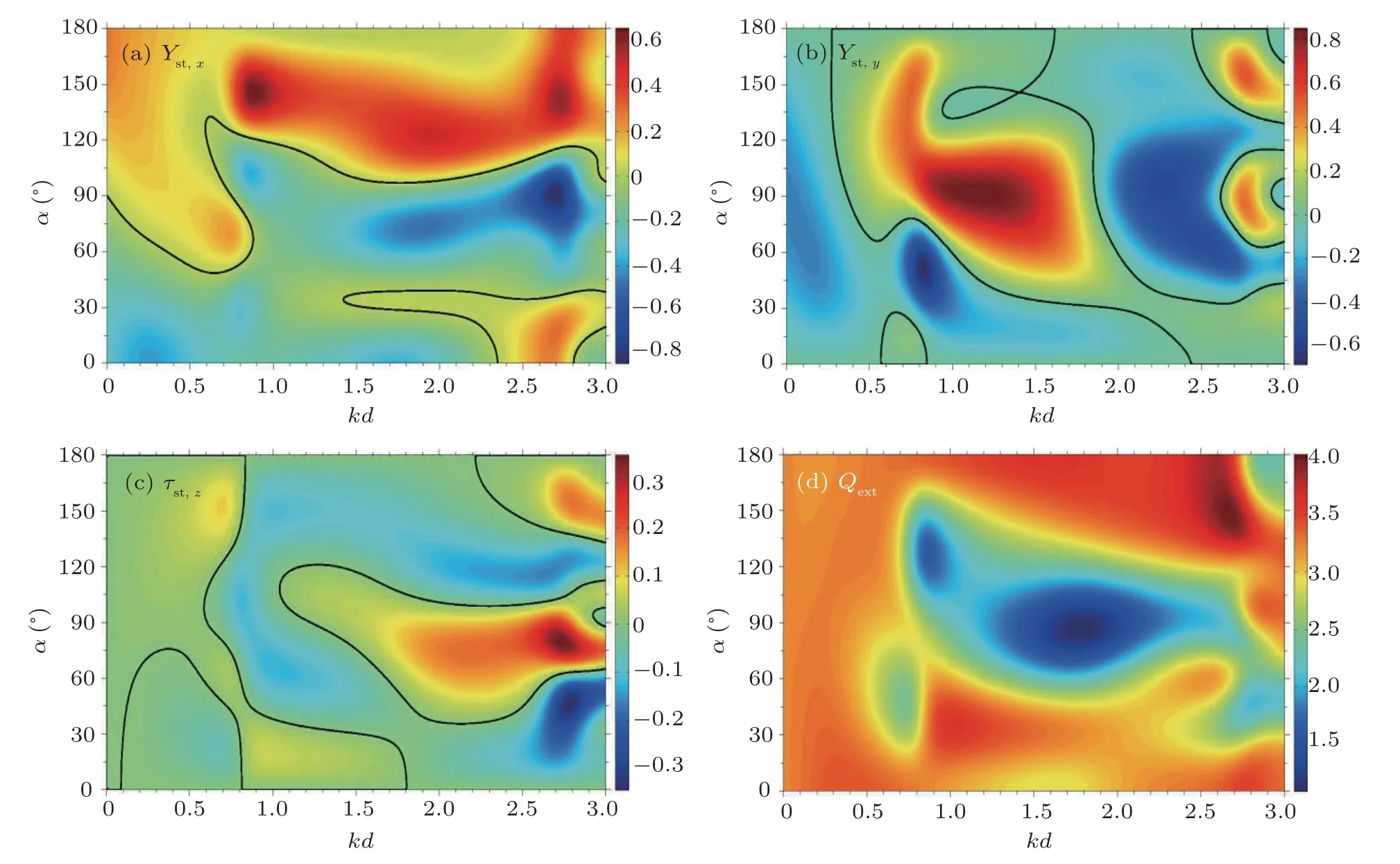
Fig.7. Panels(a)–(d)display the 2D plots versus(kd,α)of the dimensionless efficiencies Yst,x,Yst,y,τst,z,and Qext,respectively,for ka=5 and kb=2. The inner cylindrical core is composed of water,while the layer is made of mercury.

Lastly,the effect of varying ka and kd for fixed values of kb and α is investigated. As discussed previously,the constraint kd ＜(ka−kb)is imposed in the simulations. The corresponding results are displayed in panels(a)–(d)of Fig.8 for kb=0.1 and α =45◦. The plots in panels(a)–(c)show that as the non-dimensional size parameter ka and eccentricity kd vary,the acoustic radiation force and torque components alternate between positive, negative, and neutral values. Panel (d) shows that Qextis positive,in agreement with the law of energy conservation applied to scattering. As the dimensionless size parameter of the inner core cylinder increases to kb=1,changes arise in the plots of the radiation force,torque,and extinction efficiency as displayed in panels(a)–(d)of Fig.9. Positive,negative,and neutral values of the physical observables are noted. Moreover,as the incidence angle increases to α =90◦, the radiation force, torque, and extinction efficiency plots are altered as shown in panels (a)–(d)of Fig.10. As such, it is obvious that the radiation force, torque and extinction/scattering efficiencies are very sensitive to the variations of ka,kb,kd,and α.

Fig.8. Panels(a)–(d)display the 2D plots versus(ka,kd)of the dimensionless efficiencies Yst,x,Yst,y,τst,z,and Qext,respectively,for kb=0.1 and α =45◦.The inner cylindrical core is composed of water,while the layer is made of mercury.

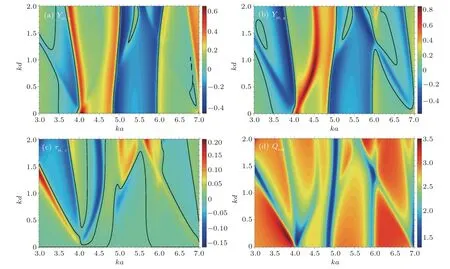
Fig.9. Panels(a)–(d)display the 2D plots versus(ka,kd)of the dimensionless efficiencies Yst,x,Yst,y,τst,z,and Qext,respectively,for kb=1 and α =45◦. The inner cylindrical core is composed of water,while the layer is made of mercury.

Fig.10. Panels(a)–(d)display the 2D plots versus(ka,kd)of the dimensionless efficiencies Yst,x,Yst,y, τst,z, and Qext, respectively, for kb=1 and α =90◦.The inner cylindrical core is composed of water,while the layer is made of mercury.

4. Conclusion

In this work, mathematical expressions for the acoustic radiation force and torque components for an eccentric layered cylinder composed of a non-viscous inner core, layered by another non-viscous fluid shell material in acoustic standing waves are derived analytically and computed. As the eccentricity of the cylinder varies,negative,positive or neutral(i.e.,zero) radiation force and torque components arise depending on the size parameters of the layer ka and inner cylinder kb as well as the eccentricity kd and angle of incidence in the polar plane. The results demonstrate that the axial radiation torque efficiency in acoustic standing waves arises,not as a result of absorption(as discussed previously in Ref.[25]),but as a consequence of a geometrical symmetry breaking as the eccentricity deviates from zero. This asymmetric behavior causing the generation of a windmill torque has been also observed in the context of elliptical cylinders.[23]Moreover, since the eccentric cylinder considered here is infinitely long,it is anticipated that the results would remain valid for an elongated particle where edge effects are neglected. In addition,the verification and validation of the results obtained here have been accomplished from the standpoint of the energy conservation law applied to scattering.The results may be used to advantage in the design and optimization of acoustical standing wave tweezers for the manipulation and rotation of eccentric elongated compound particles in fluid dynamics applications and related research.

Although the configuration studied in this paper is a 2D case, it is important in several aspects. First, the elongated cylindrical geometry has attracted significant attention in various studies,as demonstrated by numerous analyses where the 2D results have been utilized in experimental design. Second,the physical knowledge gained from the study of the 2D geometry(such as the emergence of positive, negative and neutral forces and torque) can be directly extended to the threedimensional (3D) problem as well. This is, however, not to dismiss the interest of studying radiation forces and torques for 3D geometries such as eccentric spheres or spheroidal particles,[51,52]which are still most commonly used in modeling experiments in acoustic manipulation and tweezers. It is expected that this work may generate some interest to further extend the scope of this study to account for a particle with an arbitrary-shaped geometry(in 3D)using the T-matrix formalism[53,54]or other methods.

A plausible extension of this work concerns the consideration of multiple cylindrical eccentric particles,where interparticle forces[55]and torques[56]can arise. Computations for the interparticle radiation forces and torque may be performed by extending the scope of the previous works[55,56]to account for the complex(eccentric)geometry,and earlier formulations for the extrinsic and intrinsic scattering,extinction and absorption energy efficiencies (and cross-sections)[44,57]can be utilized for verification and validation purposes based on the law of energy conservation in multiple acoustic scattering.

Appendix A:Partial-wave series expressions using the addition theorem

The addition theorem for cylindrical wave functions[43,58,59]is used to express the individual mode in the coordinate system(r′,θ′)as an infinite sum of wave functions in the other coordinate system(r,θ)(and vice versa)as

Appendix B:Partial-wave series expressions for the radiation force and torque

For the reader’s convenience, the partial-wave series used to derive the expressions for the components of the acoustic radiation force and torque are given as follows.

Based on Eqs.(2),(3),and(10),the partial-wave series expression for the term Re{Φis(r,θ)}is expressed as

Based on Eqs.(2),(3),and(16),the partial-wave series expression for the term

is decomposed into three components as,