Theoretical research on terahertz wave generation from planar waveguide by optimized cascaded difference frequency generation∗

Zhongyang Li(李忠洋), Jia Zhao(赵佳), Wenkai Liu(刘文锴), Qingfeng Hu(胡青峰),Yongjun Li(李永军), Binzhe Jiao(焦彬哲), Pibin Bing(邴丕彬),Hongtao Zhang(张红涛), Lian Tan(谭联), and Jianquan Yao(姚建铨)

1College of Electric Power,North China University of Water Resources and Electric Power,Zhengzhou 450045,China

2College of Surveying and Geo-informatics,North China University of Water Resources and Electric Power,Zhengzhou 450045,China

3College of Precision Instrument and Opto-electronics Engineering,Institute of Laser and Opto-electronics,Tianjin University,Tianjin 300072,China

Keywords: terahertz wave generation,optimized cascaded difference frequency generation,planar waveguide

1. Introduction

Terahertz(THz)waves have extensive scientific and technological applications, such as spectroscopy, biomedical engineering, communication, non-destructive inspection, and imaging fields.[1–5]However, intense and inexpensive THz wave sources are still difficult to realize, which hinders the development of THz wave applications. In order to achieve intense THz waves from optical waves by frequency conversion technology, a single optical photon must produce several THz photons due to the large ratio between optical and THz frequencies. Cascaded difference frequency generation(CDFG) is a promising method to generate numerous THz photons from a single pump photon.[6–10]CDFG involves cascaded Stokes processes in which THz photons are generated and cascaded anti-Stokes processes in which THz photons are consumed. The more cascaded Stokes processes are stimulated, the more THz photons are generated. However, the phase mismatches of the cascaded Stokes processes increase rapidly with the cascading orders, which restricts the energy transfer from pump wave to THz wave.[10]Therefore, how to reduce the phase mismatches of cascaded Stokes processes and enlarge the phase mismatches of cascaded anti-Stokes processes simultaneously is of vital importance.

In this work, we propose a novel scheme that paves the way toward high-efficiency THz wave generation by optimized cascaded difference frequency generation (OCDFG)with a planar waveguide. The modulation of THz wave effective refractive index by changing the thickness of planar waveguide can lead to the phase mismatches of cascaded Stokes processes equalling zero one by one from the firstorder Stokes process to high-order Stokes processes. At the same time,the phase mismatches of cascaded anti-Stokes processes are enlarged. Compared with reported CDFG, more pump photons are transferred to high-order cascaded Stokes processes by OCDFG,yielding an optical-to-THz energy conversion efficiency of 25.8% by OCDFG with 3000 MW/cm2pump intensity at 100 K.

2. Theoretical model

The guiding mode can exist in the planar waveguide structures,such as TE and TM guiding modes for the THz wave.[11]The phase-matching condition of the first-order Stokes process in the waveguide is expressed as

where n and λ represent refractive index and wavelength,the subscripts p,s,and T represent pump wave,signal wave,and THz wave. neff,THzis the effective refractive index of the fundamental TM-mode THz wave. The relationship between effective refractive index neff,THzand waveguide thickness t is obtained from the following equation:[11]The effective refractive index neff,THzof the fundamental TMmode THz wave varies with the thickness of the waveguide.

According to the principle of OCDFG,the incident pump wave (ω0) interacts with the first-order Stokes wave (ω1) to generate THz photon (ωT). Given that the phase-matching condition of the first-order Stokes process is satisfied,the amplified first-order Stokes wave (ω1=ω0−ωT) acts as a new high-frequency pump wave to generate second-order Stokes wave (ω2=ω1−ωT) and THz wave. As long as the phasematching OCDFG processes continue, a series of cascaded Stokes waves with frequencies of ωmspectrally separated by the THz frequency ωTare generated. The integer m denotes the m-th order cascaded optical waves. Meanwhile,the generated THz wave interacts with the incident pump wave by sumfrequency generation (SFG), generating the first-order anti-Stokes wave ω−1(ω−1=ω0+ωT).If this process continues,a series of cascaded anti-Stokes waves ω−mare generated. The coupled wave equation of OCDFG can be derived from the common nonlinear optical three-wave interaction equations

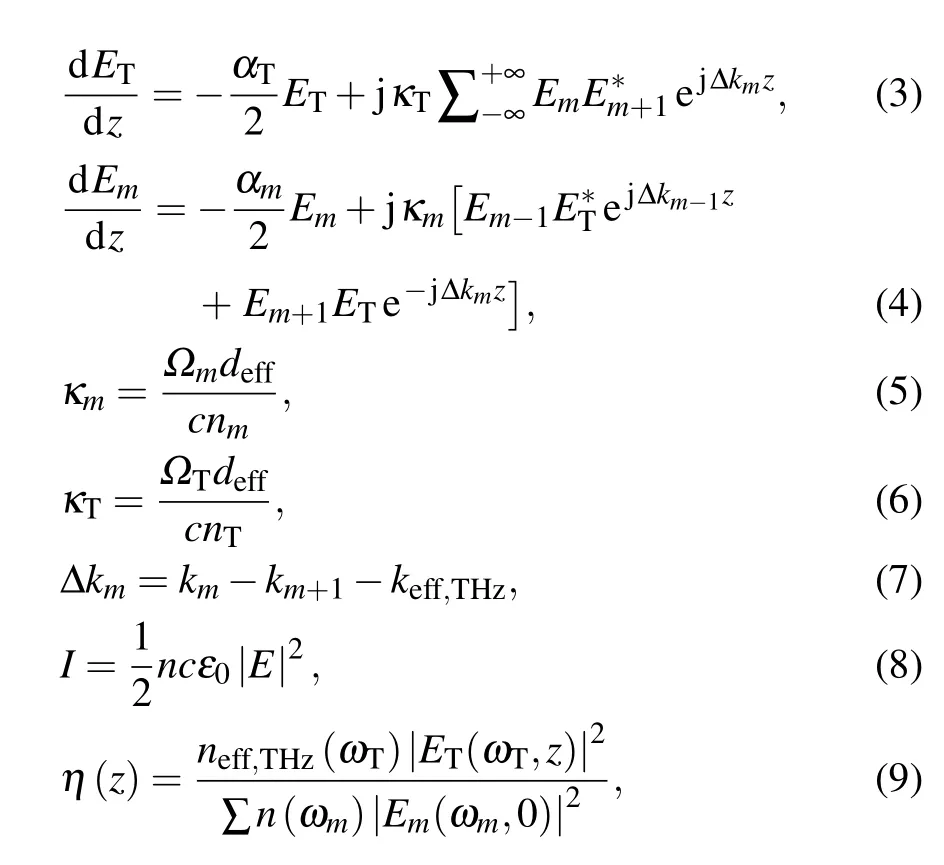
where E denotes the electric field amplitude, α denotes the absorption coefficient, κ is the coupling coefficient, Ω is the angular frequency, k is the wave vector in the waveguide, ∆k is the phase mismatch,deffis the nonlinear coefficient,c is the speed of light in vacuum,I is the power density,ε0is vacuum dielectric constant. η(z) is the energy conversion efficiency along with the waveguide length z. The first term of the righthand side of Eq. (3) indicates the THz wave absorption, and the second term represents the sum of the THz wave intensity generated by the interaction between ωmand ωm+1during the OCDFG. The first term of the right-hand side of Eq. (4)indicates the absorption of cascaded optical waves, the second term represents the enhancement of ωmby the interaction between ωm−1and ωT,and the third term represents the consumption of ωmby the interaction between ωm+1and ωT.

3. Calculations

In this section, we take MgO:LiNbO3planar waveguide as an example. The input pump frequency ωpis 291.76 THz,and ωTis 0.5 THz.The absorption coefficients of the cascaded optical waves and terahertz waves in MgO:LiNbO3waveguide are 0 cm−1and 2.10 cm−1at 100 K, respectively.[12]The nonlinear coefficient of MgO:LiNbO3at 291.76 THz is 336 pm/V.[7]The theoretical values of the refractive index of MgO:LiNbO3in the infrared region[13]and THz region[12]are calculated using the wavelength- and temperature-dependent Sellmeier equations, respectively. The laser damage threshold of MgO:LiNbO3with the pulse duration of 100 ps is～10 GW/cm2.[14]The frequency range of cascaded optical waves is set from 100.26 THz to 500.26 THz.

According to Eq. (7), the phase mismatch of mth-order CDFG changes with the effective refractive index neff,THz,so the planar waveguide thickness t can modulate the phase mismatches of cascaded Stokes processes and cascaded anti-Stokes processes. In this section,we analyze the enhancement of the cascaded Stokes processes and suppression of the cascaded anti-Stokes processes through varying the thickness of the planar waveguide.

3.1. Planar waveguide with a nonlinearly changing thickness

When each-order ∆kmequals zero, the required planar waveguide thickness t is shown by the red curve in Fig.1(a).It can be seen that in cascaded Stokes frequencies,the waveguide thickness tdecreases at first and then increases with the cascading Stokes orders, while in the cascaded anti-Stokes frequencies, the waveguide thickness t monotonously increases with the cascading anti-Stokes orders. If the waveguide thickness t is designed to vary with the change of the red curve in the cascaded Stokes frequencies from 291.76 THz to 100.26 THz,the phase mismatch ∆kmin cascaded Stokes processes is equal to zero one by one from the first-order Stokes process to highorder Stokes processes.Simultaneously,the phase mismatches|∆km|in cascaded anti-Stokes processes substantially increase,as shown in Fig.1(b). The schematic diagram of the thickness variation of the waveguide is shown in the inset of Fig.1(a),where L is the waveguide length, and w is the waveguide width.The waveguide thickness changes along with the length from t1to t2.

THz wave intensities and the evolutions of cascaded optical spectra with a nonlinearly changing thickness waveguide are calculated according to Eqs. (3) and (4) and shown in Fig.2. In Fig.2(a),with pump intensity Ip=Is=1 GW/cm2,THz wave intensities increase rapidly and reach the maximum value of 0.328 GW/cm2at 11.4 mm, and then decrease fast.In Fig.2(b) with Ip= Is= 3 GW/cm2, THz wave intensities increase continuously and reach the maximum value of 1.549 GW/cm2at 6.9 mm. It can be seen from Fig.2(a) that in the initial stage,THz wave intensities increase slowly. For 4 mm＜z ＜11.4 mm,THz wave intensities increase fast as the diffusion range of the cascaded Stokes frequencies rapidly increases.For z>11.4 mm,the diffusion range of cascaded anti-Stokes frequencies is gradually larger than that of cascaded Stokes frequencies, so the THz wave intensities decrease. In Fig.2(b),THz wave intensities show a monotonously upward trend for 0 mm＜z ＜6.9 mm, and the diffusion range of cascaded Stokes frequencies is obviously larger than that of cascaded anti-Stokes frequencies. Compared with the energy conversion efficiency of 16.4% in Fig.2(a), the energy conversion efficiency of 25.8%in Fig.2(b)are greatly improved.Moreover,the diffusion ranges of cascaded Stokes frequencies in Fig.2(c) is smaller than those in Fig.2(d), and the diffusion ranges of cascaded anti-Stokes frequencies in Fig.2(c)is larger than those in Fig.2(d).Higher pump intensities produce wider diffusion ranges of cascaded Stokes frequencies and narrower diffusion ranges of cascaded anti-Stokes frequencies,resulting in higher THz wave intensities and energy conversion efficiencies. It can be observed from Fig.2(d) that the diffusion ranges and the intensities of cascaded Stokes waves are larger than those of cascaded anti-Stokes waves.The above results demonstrate that the cascaded Stokes processes are significantly enhanced, and the cascaded anti-Stokes processes are effectively suppressed by using the planar waveguide with nonlinearly changing thickness.

Fig.1. (a) The waveguide thickness versus the cascaded optical frequency when ∆km is equal to 0. Inset: schematic diagram of the planar waveguide with changing thickness. (b)The nonlinearly changing thickness and normalized|∆km|versus the cascaded optical frequency.

Fig.2. THz wave intensities and optical spectra with nonlinearly changing thickness waveguide. The red curves in(a)and(b)represent the variation of the THz wave intensity, and the dashed-line arrow indicates the right longitudinal axis. (a) Ip =Is =1 GW/cm2. (b) Ip =Is =3 GW/cm2. (c)Optical spectra corresponding to(a). (d)Optical spectra corresponding to(b).

3.2. Planar waveguide with a constant thickness

In this part, we analyze THz wave generations from traditional CDFG with a constant thickness MgO:LiNbO3planar waveguide. THz wave intensities and the evolutions of cascaded optical spectra with a constant thickness waveguide are shown in Fig.3. In Fig.3(a) with Ip=Is=1 GW/cm2,THz wave intensities increase slowly and reach the maximum value of 107.1 MW/cm2at z=5.6 mm,and in Fig.3(b)with Ip=Is=3 GW/cm2, THz wave intensities increase continuously and reach the maximum value of 475.8 MW/cm2at 4.0 mm. Compared with energy conversion efficiencies of 16.4% in Fig.2(a) and 25.8% in Fig.2(b), energy conversion efficiencies of 5.4% in Fig.3(a) and 7.9% in Fig.3(b)are greatly suppressed. It can be seen from Fig.3(c) that the cascaded Stokes frequencies and the cascaded anti-Stokes frequencies at each waveguide length only diffuse to a very small frequency range. It can be observed from Fig.3(d) that in the range from z=0 mm to z=1.5 mm,the cascaded Stokes frequencies and the cascaded anti-Stokes frequencies diffuse slowly,and most of the pump energy is still concentrated near the pump frequency.For 1.5 mm＜z ＜3 mm,the intensities of cascaded Stokes waves are obviously higher than those of cascaded anti-Stokes waves. For 3 mm＜z ＜4 mm, the generation rate of THz photon is enhanced as the cascaded Stokes frequencies rapidly diffuse to higher cascading orders.The diffusion ranges of cascaded optical frequencies in Figs.3(c)–3(d)are substantially smaller than those in Figs. 2(c)–2(d). Since the waveguide thickness remains constant,both the phase mismatches ∆kmin cascaded Stokes processes and cascaded anti-Stokes processes increase with the cascading orders. The cascaded anti-Stokes processes consume large numbers of generated THz photons,which suppresses the cascaded Stokes processes,resulting in a decrease of THz wave intensities.

Fig.3. THz wave intensities and optical spectra with constant thickness waveguide. The red curves in(a)and(b)represent the variation of the THz wave intensity,and the dashed-line arrow indicates the right longitudinal axis. (a)Ip=Is=1 GW/cm2. (b)Ip=Is=3 GW/cm2. (c)Optical spectra corresponding to(a). (d)Optical spectra corresponding to(b).

3.3. Planar waveguide with a linearly changing thickness

In this part,we propose a planar waveguide with a linearly changing thickness,as shown in Fig.1(a)with the black curve.The black curve is divided into two parts trand tl. trchanges from the thickness corresponding to the first-order phasematching cascaded Stokes process to the minimum thickness of the red curve in Fig.1(a), and tlchanges from the minimum thickness to the thickness corresponding to the highestorder phase-matching cascaded Stokes process. trand tlare expressed as

The unit of trand tlisµm. fpand fTrepresent the frequency of pump wave and THz wave,respectively,and the unit of fpand fTis THz. N is the number of cascaded Stokes frequency,and L is the optimal waveguide length.

Fig.4.THz wave intensities and optical spectra with linearly changing thickness waveguide.The red curves in(a)and(b)represent the variation of the THz wave intensity,and the dashed-line arrow indicates the right longitudinal axis. (a)Ip =Is =1 GW/cm2. (b)Ip =Is =3 GW/cm2.(c)Optical spectra corresponding to(a). (d)Optical spectra corresponding to(b).

THz wave intensities and the evolutions of cascaded optical spectra with a linearly changing thickness waveguide are shown in Fig.4. In Fig.4(a) with Ip=Is=1 GW/cm2, THz wave intensities increase slowly and reach the maximum value of 327.5 MW/cm2at z=12.2 mm,and in Fig.3(b)with Ip=Is=3 GW/cm2,THz wave intensities increase monotonously and reach the maximum value of 1.495 GW/cm2at z =7.4 mm. Compared with energy conversion efficiencies of 16.4%in Fig.2(a)and 25.8%in Fig.2(b),energy conversion efficiencies of 16.38%in Fig.3(a)and 24.92%in Fig.3(b)are slightly decreased. The diffusion ranges and the intensities of cascaded optical waves are broadly similar to those in Fig.2.As shown in Fig.1(a), the differences between the red curve and the black curve at the same frequency are minimal,which ensures that the phase mismatches ∆kmwith a linearly changing thickness waveguide are close to those with a nonlinearly changing thickness waveguide. The planar waveguide with a linearly changing thickness is convenient to manufacture and shows a result analogous to that with a nonlinearly changing thickness.

4. Discussion

Compared with the maximum energy conversion efficiency of 7.9%from traditional CDFG with a constant thickness waveguide shown in Fig.3(b), the maximum energy conversion efficiency is enhanced by 3.27 and 3.15 times by OCDFG from the planar waveguide with a nonlinearly changing thickness and a linearly changing thickness, respectively.Compared with the reported theoretical work with an energy efficiency of 8%by CDFG with PPLN at 77 K,[15]the energy efficiency of 25.8%in this work is attributed to the decrease of phase mismatches in cascaded Stokes processes and increase of phase mismatches in cascaded anti-Stokes processes simultaneously. OCDFG proposed in this work can efficiently generate THz frequencies in the range of 0.1–3 THz with low THz wave absorption coefficients. The scheme can be applied to other planar waveguides,such as GaAs,GaP.

In practice, experimental setups mainly consist of a planar waveguide and two pump lasers with frequencies separated by the generated THz frequency. The two pump lasers can be realized by a compact broadband Q-switched Yb:YAG laser[16]or by a KTP-OPO at the degeneracy point.[17]The planar waveguide with a linearly changing thickness is convenient to manufacture,while the planar waveguide with a nonlinearly changing thickness is difficult to manufacture. The existing manufacturing technology for two pump lasers and planar waveguide with a linearly changing thickness makes high-efficiency THz wave generation by OCDFG practically feasible.

5. Conclusion

We propose a novel scheme for high-efficiency THz wave generation based on OCDFG with a planar waveguide. By designing the planar waveguide with a nonlinearly or linearly changing thickness,the phase mismatches of cascaded Stokes processes equal zero one by one from the first-order Stokes process to high-order Stokes processes, while the phase mismatches of cascaded anti-Stokes processes fundamentally increase. As a result,the modulated phase mismatches enhance the cascaded Stokes processes and suppress the cascaded anti-Stokes processes simultaneously, yielding energy conversion efficiencies over 25%at 100 K.