A multi-directional controllable multi-scroll conservative chaos generator: Modelling,analysis,and FPGA implementation∗

En-Zeng Dong(董恩增), Rong-Hao Li(李荣昊), and Sheng-Zhi Du(杜升之)

1Tianjin Key Laboratory for Control Theory&Applications in Complicated Systems,Tianjin University of Technology,Tianjin 300384,China

2Department of Electrical Engineering,Tshwane University of Technology,Pretoria 0001,South Africa

Keywords: multi-directional controllable multi-scroll, conservative chaos, coexisting flows, field programmable gate array(FPGA)

1. Introduction

With the discovery of Lorenz chaotic oscillator in 1963,the researches on chaos have achieved many important progresses.[1–4]In general, chaotic systems can be classified into two categories: dissipative chaos and conservative chaos.[5]There are many physical models of dissipative chaos in natural world. Theoretically,the phase space volume of dissipative chaos is collapsed.[6–8]

Different from the dissipative chaos, each trajectory in phase space of conservative chaos does not approach the equilibrium points finally with passage of time, which indicates there is no attractor in conservative chaos.[9]Moreover,there are some interesting discoveries on conservative chaos.Firstly,the positive and negative Lyapunov exponents are symmetric about zero.[10,11]Secondly, the Hamiltonian energy of the conservative chaos is a constant, which is only determined by the initial values,and the system trajectory in phase space motions on the energy equivalent hyper-sphere.[12]Duo to the better ergodic property, conservative chaos is more suitable for information encryption.[13,14]Furthermore,multiscroll conservative chaos have more complex dynamical behaviors. The complexity of time series varies with the number of scrolls.[15–20]If the scrolls can be controlled, the systems can be applied to the engineering field more effectively.[21–28]

Coexistence behavior dependent on initial condition is one of the most significant characteristics in chaotic systems and it has great potential value in chaos-based engineering applications such as the design of pseudo-random signal generating circuits.[29–33]Although there is no attractor in conservative chaos,a little change of initial condition will lead to the change of Hamiltonian energy,which can result in the coexistence of multiple flows.[34]

In 1984, Chua proposed a chaotic system with multiscroll and constructed the corresponding circuit model,which firstly built a bridge between chaos and nonlinear circuits.[35]Then, some multi-scroll dissipative chaotic systems were proposed and implemented by nonlinear circuits.[36–40]The chaos-based circuits consist of analog circuit and digital circuit realizations.[41]Analog chaotic circuits are susceptible to the influence of the environment resulting in parameter changes.[42]Compared with the analog circuits, because of the reprogrammable, low costs, stable operation, computational rapidity, FPGA chips are most suitable for the implementation of chaos-based generators.[43]Sadoudi et al. implemented the Chen system on a FPGA chip by using the fourthorder Runge–Kuta(RK4)algorithm.[44]Compared to the RK4 method, the Euler algorithm is easy to realize and convergent,and the error is within the acceptable scale.[45]Wang et al. proposed a hyper-chaotic system which was implemented physically by FPGA chips using the Euler algorithm.[46]

The above works mainly focus on dissipative chaotic circuits implementation. Due to more uniform and dense orbits,the circuit implementation of conservative chaos is more difficult. Furthermore, because of the better ergodicity of multiscroll conservative chaotic flows, it is more challenging to implement multi-scroll conservative chaotic circuits by FPGA platform.

In this paper,a novel multi-directional controllable multiscroll conservative chaos is constructed. The content of the paper is arranged as follows. In Section 2, combing with the generalized Hamiltonian system theory, the multi-directional controllable multi-scroll conservative chaotic system is constructed. In Section 3, the conservativity and dynamics characteristics including bifurcation and coexistence behaviors of the proposed system are revealed. In Section 4,the NIST tests are carried out to verify the randomness of time series and the FPGA circuits are designed. Some experimental results are presented for verification and show good ergodicity.

2. A novel multi-directional controllable multiscroll conservative chaos

A kind of multi-scroll conservative chaotic system with infinite equilibria is constructed in Ref. [10] and the mathematical model is given as follows:

According to the generalized Hamiltonian system theory,[47]system(1)can be represented as follows:

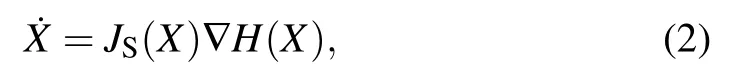
in which JS(X) is the interconnection conservation matrix and ∇H(X)represents the gradient of the Hamiltonian energy function.

One can deduce

which is a skew symmetric matrix.The gradient of H(X)is

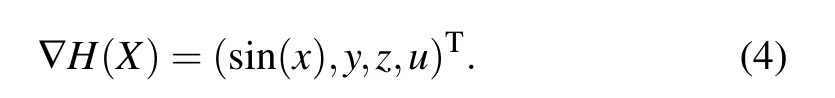
To construct n-dimensional (n = 1,2,3) controllable multi-scroll conservative chaos, for system (1), assume∇H(X) = (g(x),h(y),d(z),u)Tand the interconnection conservation matrix is

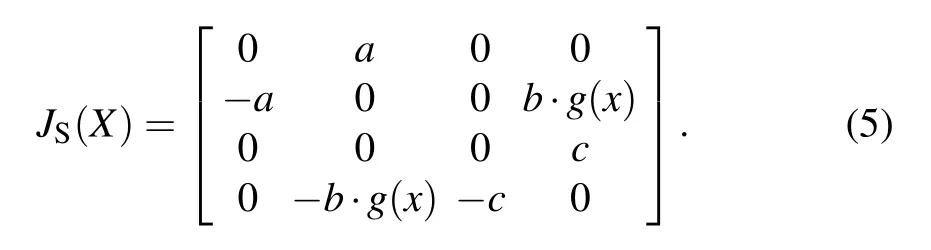
The equilibrium points are determined by

To control the distribution of the equilibria,we just need control the solutions of Eq.(6). Combining the sine function with the piecewise function,solutions control can be achieved.The function can be expressed as follows:

Introducing the proposed function to system(1),the distribution of equilibria can be divided into three cases, which are shown in Fig.1.

Fig.1. Distribution of equilibrium points: (a)1D case;(b)2D case;(c)3D case.

2.1. Constructing 1D controllable multi-scroll conservative chaos

Transform ∇H(X)as(f(x),y,z,u)Tand the interconnection conservation matrix JS(X)as follows:

One can obtain a novel 1D controllable multi-scroll conservative chaotic system as follows:

Let ˙x= ˙y= ˙z= ˙u=0, the equilibria set(kπ,0,0,0),k ∈[−2n,2n]∩Z can be obtained, which indicates the number of equilibia of system (9) is always related to the piecewise points. The corresponding Jacobian matrix is

Set parameters (a,b,c) as (6,4,6) and the initial values(x0,y0,z0,u0) as (1.9,1,1,1). By calculating the characteristic equation roots of the Jacobian matrix, one can conclude that the points(2kπ,0,0,0),k ∈[−n,n]are center points with eigenvalues(6i,−6i,6i,−6i)and(kπ,0,0,0),k ∈[−n,n]∩Z∗are unstable saddle points with eigenvalues (6,−6,6i,−6i).Figure 2 depicts the phase portraits in x–y plane with different values of n,in which the red dots represent the center points.It is found that the scrolls always emerge from the neighborhood of the center points,and the bond orbits are generated from the neighborhood of the unstable saddle points.

Fig.2. Phase diagrams in x–y plane of 1D controllable multi-scroll conservative chaos with respect to n: (a)n=1;(b)n=2;(c)n=3;(d)n=4.

2.2. Constructing 2D and 3D controllable multi-scroll conservative chaos

Similarly, transform ∇H(X) as (f(x),f(y),z,u)T, (4n+1)·(4n+1) equilibrium points can be obtained and the corresponding Jacobian matrix eigenvalues are listed in Table 1.Through calculating, the unstable saddle points and the center points are cross-distributed in the x–y plane,which makes it possible for the system to generate 2D multi-scroll chaotic flow. Set the parameters and the initial conditions the same as the above,figure 3 depicts the phase portraits in x–y plane with different piecewise points. One can see that 2D controllable scrolls can be generated along x-direction and y-direction,and the scrolls just emerge from the neighborhood of the marked center points.

For generating 3D controllable multi-scroll conservative chaos, transform ∇H(X) as (f(x),f(y),f(z),u)T, then,(2n+1)·(2n+1)·(2n+1) scrolls can be generated along x-direction, y-direction, and z-direction. The phase portraits with different n are shown in Fig.4. One can see that the scrolls just emerge from the neighborhood of the marked equilibria(2 jπ,2kπ,2lπ,0),j,k,l,∈[−n,n].

Fig.3. Phase diagrams in x–y plane of 2D controllable multi-scroll conservative chaos with respect to n: (a)n=1;(b)n=2;(c)n=3;(d)n=4.

Table 1. Equilibrium points and the corresponding eigenvalues.

Fig.4. Phase diagrams in x–y–z space of 3D controllable multi-scroll conservative chaos with respect to n: (a)n=1;(b)n=2;(c)n=3;(d)n=4.

3. Analysis of the proposed system

3.1. Energy analysis

Recently, Hamiltonian energy-based analysis method is widely used for analyzing the dynamics behaviors of nonlinear systems. According to Helmholtz’s theorem, the vector field F(X)of system(9)can be expressed as follows:

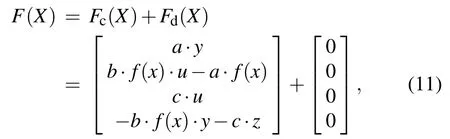
By solving the equation ∇HT(X)Fc(X)=0,one can obtain the Hamiltonian energy function. Due to the existence of piecewise term,the solutions need to be discussed as follows.

(1)When x ＜−2nπ,one can obtain f(x)=x+2nπ and the solution is

(2)When −2nπ ≤x ≤2nπ, f(x)=sin(x). The Hamiltonian energy function can be expressed as

(3)When x ≥2nπ, f(x)=x −2nπ,the Hamiltonian energy function can be expressed as

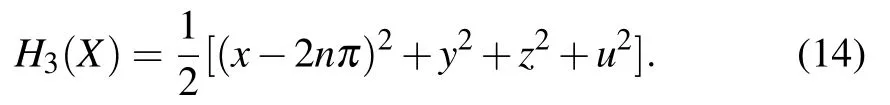
Moreover,the time domian derivative of the Hamiltonian energy function is

低附加值向高附加值转变。传统的出版业向读者所提供的产品仅仅是纸质图书，所提供的服务几乎没有附加值。在转型升级的语境下，通过二维码、微信公众号、关联数据库平台或者网站，为用户提供增值知识服务，使得用户在原有的图书知识基础上能够享受到额外的知识服务，这是低附加值向高附加值转变的体现之一。在功能上，传统出版所提供的主要是整体阅读功能，转型升级语境下的新兴出版，向着碎片化阅读，查询、复制、粘贴、知识关联和知识图谱的方向进化，这也是高附加值的重要体现。

which illustrates that the Hamiltonian energy of system (9)is locally invariable. It should be denoted that the energy of scrolls is always not equal to the energy of the marginal bond orbits.

3.2. Volume conservativity

According to Liouville’s theorem,[48]the rate of volume change is

Furthermore,the divergence of system(9)is

One can conclude that the proposed system is a volumeconservative nonlinear dynamics system, which is also characterized by the fact that the sum of the Lyapunov exponents always approximates to zero over time.

3.3. Dynamics behaviors with varying parameter b

In order to investigate the dynamical behaviors with the change of parameter b,let parameters a=6,c=6 and initial conditions (x0,y0,z0,u0) = (1.9,1,1,1). The corresponding bifurcation diagram and Lyapunov exponents spectrum with increasing parameter b from −6 to 6 are shown in Figs. 5(a)and 5(b),respectively. One can see the effect of the parameter b on the dynamics behaviors of system(9).In particular,when b ∈[−0.42,0.08],the bifurcation diagram shows the different quasi-periodic orbits.

Fig.5. Dynamics behaviors of system(9)with respect to b. (a)Bifurcation diagram;(b)Lyapunov exponents spectrum.

3.4. Coexisting conservative motions

For system(9), in order to fully observe the influence of the initial values x(0)and y(0), the system parameters a=6,b=4, c=6, n=1 and initial values z(0)=1, u(0)=1 are chosen, then, various coexisting flows can be found and the dynamical evolution map is shown in Fig.6, in which the parts of cyan,purple,red,and yellow represent different quasiperiodic states and the blue region represents the multi-scroll conservative chaotic flow. Under different initial conditions(ICs), some coexisting quasi-periodic orbits obtained by numerical simulation are shown in Fig.7, which indicates rich coexistence behaviors.

Furthermore, by analyzing the symmetry property, one can deduce that,when(x,y,z,u)is the solution of system(9),(−x,−y,z,u) is also the solution of system (9), which means any orbit has a symmetrical orbit with regard to the zou-plane.Therefore,for the flows in the red and purple regions,there are coexisting symmetrical flows,which are plotted in Fig.8.

Fig.6. Dynamical evolution map with different initial values of x(0)and y(0), in which the parts of cyan, purple, red, and yellow represent different quasi-periodic states and the part of blue represents chaotic state.

Fig.7. Phase portraits in x–y phase of coexisting quasi-periodic orbits with parameters set(a,b,c)=(6,4,6): (a)quasi-periodic orbit in purple region; (b) quasi-periodic orbit in cyan region; (c) quasi-periodic orbit in yellow region;(d)quasi-periodic orbit in red region.

Fig.8. Symmetrical coexisting quasi-periodic orbits: (a)quasi-periodic orbit with initial value (−0.6,−0.8,1,1); (b) quasi-periodic orbit with initial value(−1,−1,1,1).

4. FPGA implementation

4.1. Design of FPGA circuits

In order to implement the proposed system,sinusoidal operation needs to be implemented with minimal error firstly.The 10Q45 signed fixed-point format is adopted here to ensure the accuracy. Utilizing the graphical modules in DSPBuilder provided by Altera, the sine operation module is designed. Firstly,define two maps as follows:

Choosing n=6,for the arbitrary signal x ∈[−π/2,π/2],the sine approximation can be obtained by calculating Taylor’s formula. Generally, to compute the sine approximation value of the signal x ∈R, it needs to be normalized to the interval x ∈[−π/2,π/2].

Considering the periodic property, the Divider block is called firstly to convert the value of the signal to the interval[−2π,2π],the relevant expression is

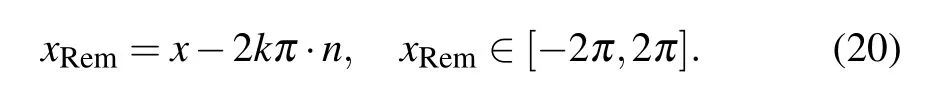
Then Comparator-1 is called to judge the range of the value of xRem,if the value is in the interval(0,2π],the parallel adder Subtractor-1 is invoked to decrease the value by 2π,the mathematical expression is

Then Comparator-4 and Comparator-5 are called to judge the range of the value of xSub,if it is in the interval[−π/2,0],the Taylor arithmetic unit (TAU) is called to obtain the sine approximation of the input signal. If the value of xSubis in the interval[−3π/2,−π/2),considering the coordinate transformation and property of odd function, the parallel adder Subtractor-2 is called to increase the value by π,then the gain block is called to multiply the numerical by −1. After normalization, the sine approximation can be computed by conducting Taylor polynomial operation. If the numerical of xSubis less than −3π/2,the parallel adder Subtractor-3 is called to increase the value by 2π, then, by calling the TAU, the sine approximate value can be obtained.

Figure 9 illustrates the hardware architecture of the sine function, bits variable is put to control the data path of the multiplexer. The relationship between the value of variable and data paths is illustrated in Table 2.

Fig.9. Hardware realization of sine operation.

Table 2. Data paths description.

With the input x ∈[−5π,5π], the experimental result is presented in Fig.10(a), the obtained error compared with the computational result of the lookup table (LUT) method is shown in Fig.10(b).

To achieve the algorithm, the built-in hardware multipliers of FPGA are utilized, and the occupancy rate is about 20%. It can be seen that the maximum error is no more than 2×10−9,which illustrates a good result.

To implement the proposed chaotic system physically, it needs to be discretized. Utilizing the Euler algorithm,the discrete description of system(9)can be expressed as follows:

in which τ represents the discrete time step and k represents the discrete number.

The top-layer RTL viewer of the above realization is shown in Fig.11, and the outputs of the block include two categories. “Data outA [13:0]” and “Data_outB [13:0]” represent the outputs of each step of any two variables. The“clock_outA” and “clock_outB” are the clocks for the external DAC chip.

Fig.10. Experimental results: (a)output wave;(b)error analysis.

Fig.11. Top-layer RTL of the proposed multiscroll conservative chaos generator.

Fig.12. The experimental hardware platform for the proposed chaotic system.

The hardware platform is developed with an Altera Cyclone IV FPGA EP4CGX150DF31, an external DAC chip AD9764, and a digital oscilloscope Tektronix MSO4054B.Utilizing the D/A converter and the digital oscilloscope, one can obtain the experimental portraits generated by FPGA.The hardware architecture of this platform is shown in Fig.12.

4.2. Experimental results

4.2.1. NIST tests

Fig.13. Probability distribution of P-value for non-overlapping template.

The NIST tests are used to determine whether the time sequence meets certain characteristics of a random sequence,which include 16 tests. To finish these tests, 100 M data are needed. Divide the data into 100 groups and set other parameters as default values,one can obtain the test results consisting of the P-values and the relevant proportions. As shown in Table 3,all P-values obtained in statistical tests are greater than the significance level,α =0.01. The relevant proportions are all within [0.9601,1.0298]. It can be concluded that the tests are fully successful. Figure 13 illustrates that the distribution of P-values for the non-overlapping template is uniform. The other 14 tests also show uniformity. One can conclude that system(9)is suitable as a pseudo-random signal generator.

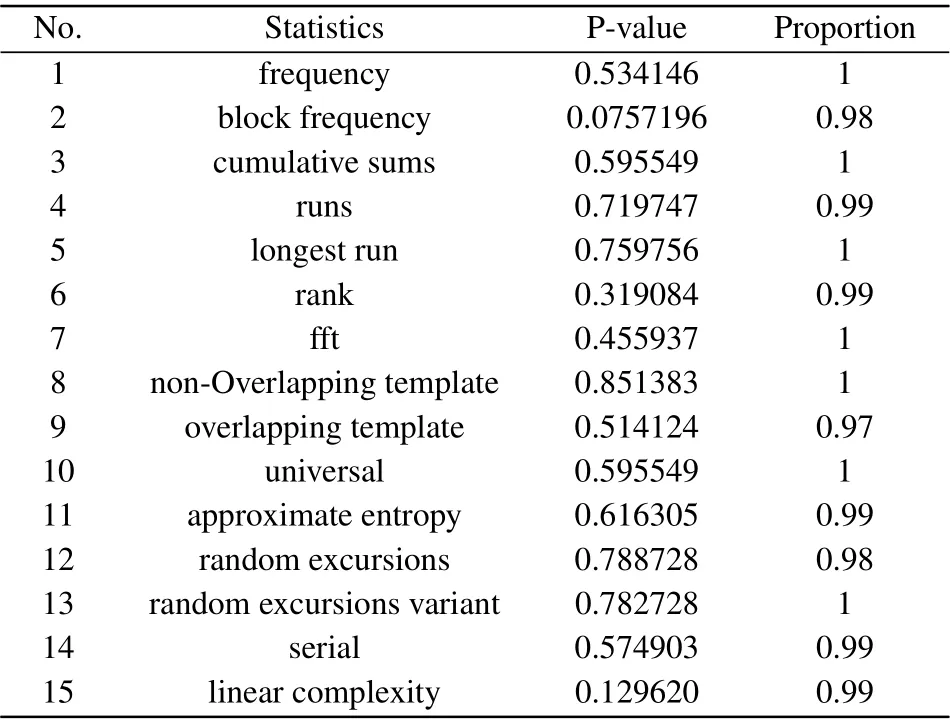
Table 3. NIST tests of the proposed system.

Fig.14. Experimental portraits of 1D,2D,3D controllable multi-scroll conservative chaos with n=2: (a)phase diagram in x–y plane of 1D case; (b) phase diagram in x–z plane of 1D case; (c) phase diagram in x–y plane of 2D case; (d) phase diagram in x–z plane of 2D case; (e)phase diagram in x–y plane of 3D case;(f)phase diagram in x–z plane of 3D case.

4.2.2. Experimental phase diagrams

Figure 14 presents the 1D,2D,and 3D controllable multiscroll conservative chaotic flows with n=2,which are consistent with the simulation results depicted in Figs. 2(b), 3(b),4(b). The experimental portraits of the proposed system show good ergodicity, so it is suitable for the application of secure communication and other engineering fields.

5. Conclusion

In this paper, based on the generalized Hamiltonian system theory, a class of multi-directional controllable multiscroll conservative chaos is proposed by controlling the number of equilibria. The bifurcation and coexistence behaviors are revealed, which illustrate the dynamics characteristics. Furthermore, the passing of the NIST tests verifies that the signal generated by the proposed system has certain characteristics of a random sequence. Finally, FPGA circuits are designed to realize the chaotic system and the circuit implementation results are consistent with the numerical simulation,all of them show good ergodicity and are suitable for information encryption and other engineering applications.