一种基于鸽群优化算法的入侵检测技术
王 康,霍朝宾,李青旭
(华北计算机系统工程研究所,北京100083)
0 引言
随着互联网使用规模的不断扩大,网络上传输的重要信息也在逐渐增加, 但也暴露出很多的安全性问题。入侵检测系统作为网络空间安全的核心组件,直接影响了网络的安全性。入侵检测的主要功能是识别网络中可能包含攻击的非正常行为。根据入侵检测功能的执行位置,可分为基于网络的入侵检测和基于主机的入侵检测。
本文将介绍一种鸽群优化算法应用于入侵检测系统。 通过提出的算法对公开数据集进行特征选择,然后用决策树对选择的特征进行建模分析。特征选择后的数据集维度显著降低,不但加快和简化了模型的建立,还提高了模型的泛化性。 在此基础上,对算法进行了一定程度改进,使其更适合于离散空间的特征选择。
1 理论基础
1.1 特征选择
特征选择是按照某种规则在原特征中选择对分类更加有益的特征子集而删除对建模无用或者有害的特征,从而简化模型以算提高算法性能。
由于特征选择是一个机器学习的概念,它主要是通过各种算法来实现的,因此经常使用统计分析、支持向量机、神经网络和数据挖掘等方法完成特征选择[1]。 此外,特征选择假设了一种检测机制,可以将其分为3 类:随机选择、递增选择和递减选择。 选择机制用于确定和选择数据集中的相关特征。 值得注意的是,特征选择可以通过多种技术实现,包括智能模式、群体智能、人工神经网络、确定性算法、模糊和粗糙集[2]。
1.2 鸽群优化算法
鸽群优化(Pigeon Inspired Optimation,PIO)算法是一种仿生群体智能算法[3]。 群体智能用于解决非确定性多项式(NP)问题或搜索空间过大的问题。 它模仿一些生物群体社会机制,试图用数学模型模拟一个群体的自然行为,以提高求解问题的质量[4]。
鸽群优化算法通过两个算子运行:地图和指南针算子与地标算子。

式中,R 是地图和指南针算子的因数,rand 是从[0,1]之间的均匀分布中随机取的,Xg为当前鸽群的全局最优解,Xi(t)、Vi(t)分别表示在t 的迭代轮次中鸽子i 的位置和速度。
图1 所示为地图和指南针算子示意图,飞行中的鸽子会根据最佳鸽子的位置调整自己的飞行方向。 式(1)中的第一个部分表示鸽子的当前方向,第二部分表示鸽子跟随最佳鸽子(当前最优解)的过程。

图1 地图和指南针算子示意图
在地标算子中,所有的鸽子会根据它们的适应度排序。 排序前一半的鸽子将根据式(3)来计算中心鸽的位置,这个位置被当作地标,其余一半的鸽子将根据这个地标来更新自己的位置,如式(4)所示。

式中,Xc是中心鸽(地标)的位置,Xi是所有鸽子的当前位置,Fitness 是适应度函数,Np(t) 是代表鸽子的数量。

图2 是地标算子的示意图,在算法模拟的过程中,认为低适应度的鸽子对地标是不熟悉的,它们必须跟随高适应度的鸽子。 图2 中的黑鸽子表示地标的位置,圈内的鸽子数量是根据式(5)计算的鸽子数的一半。


图2 地标算子示意图
2 基于鸽群优化算法的特征选择
鸽群优化(PIO)算法在解决无人机路径规划、无人机自主编队[5]、自动着陆系统[6]、PID 设计控制器[7]等诸多优化问题中得以实践。本文采用了一种基于鸽群优化的特征选择算法应用于入侵检测系统。 在本节中,提出了PIO 的两个版本。 第一个版本的算法使用Sigmoid 函数离散化鸽子向量,而第二个版本是使用离散的鸽子向量基于余弦相似度重新定义鸽子的速度。虽然两个版本都使用了相同的适应度函数,但是每个版本的算法其求解方式又不尽相同。
2.1 适应度函数
适应度函数是用来评价优化问题中求解过程的适应性。 在本文所阐述的问题中,适应度函数是根据真阳性率(TPR)、假阳性率(FPR)和特征数对所选特征子集的解进行评估的。特征的数量是参与适应度函数的计算过程的,因此如果在特征子集中加入了某个特征但不影响TPR 或FPR,则倾向于消除它。式(6)给出了本文使用的适应度函数:

式中,SF 为所选特性的数量,NF 为所有特征的数量,w1+w2+w3=1。 由 于TPR 和FPR 同 等 重 要[8],因 此 权 重 值设置如下:w1= 0.1,w2=w3=0.45。
2.2 Sigmoid_PIO 用于特性选择
在第一个PIO 特征选择的方法中,首先将速度和位置向量每一维的值被初始化为[0,1]区间的随机数。 通过式(1)计算每只鸽子的速度,然后用式(7)中的Sigmoid函数[9]转化速度向量。 如式(8)所示,为了二元化鸽子的位置向量,根据Sigmoid 函数的值和一个随机数r 来更新鸽子的位置。

式中,Vi(t)为迭代t 中的鸽子速度,r 为均匀随机数。
2.3 Cosine_PIO 特征选择算法
第二种PIO 方法的提出是为了克服第一种方法的局限性而设计的。 Cosine_PIO 使用余弦相似度来计算鸽子的速度。 Cosine_PIO 与Sigmoid_PIO 有3 个不同点:解向量(鸽子)的表示;更新位置和速度的方式;允许新的鸽子加入鸽群以增加算法达到全局最优解的机会。
Cosine_PIO 中的解是一个长度为输入数 (特征数)的向量,向量的值由0 或者1 随机初始化。 0 表示当前向量(鸽子)中没有对应的特征,1 表示当前向量中存在对应的特征。 图3 显示了一个为KDDCUP99[10]数据集随机生成的解决方案的示例。

图3 KDDCUP99 数据集上特征选择示意
2.4 修改地图和指南针算子
如前所述,PIO 的基本工作原理是用最优鸽子的位置减去当前鸽子的位置Xi,如式(1)所示。 但是当鸽子向量为离散值时,不能将离散的0、1 向量作为常规向量减法来减,因此本文用新的方式来模拟PIO 在连续问题中的减法过程来更新鸽子的速度向量。 式(9)给出了鸽子速度的计算,这里每只鸽子的速度取决于它们和最优鸽子的相似度程度。 根据式(9)求出鸽子的速度值Vp,根据式(10)来更新鸽子的位置。

其中,r 是均匀随机数。
根据式(10),如果当前鸽子不是全局解的近邻,则其有更高的概率向全局最优解更新其位置。
2.5 修改的地标算子
Cosine_PIO 的地标算子第一部分与基本PIO 基本算法相同。 先根据适应度对鸽群排序,然后计算中心鸽子(地标)的位置。
地标算子的第二部分中,鸽子更新它们达到期望目标位置的过程是不同的,因为期望目标位置是一个二元向量。 因此,所有的鸽子都会先通过式(9)计算它们的速度,然后根据式(10)更新它们的位置。
2.6 加入新鸽子
二元鸽群优化算法中的另一个变化就是以一定的可能加入新鸽子,这个想法的来源是在二元鸽群优化算法执行的过程中有很高的可能存在重复的解。鸽子的加入过程只能在地图和指南针算子中完成。如果存在重复解,则有一半的概率直接丢弃重复解,以一般的概率随机改变重复解的0.2 来加入鸽群。 这将有助于更大范围的探索解空间。
二元的解向量限制了鸽群优化的有效性,但是本文通过余弦相似度解决了向量速度的问题,通过加入适应度解决了鸽群中心位置难以计算的问题,使得鸽群优化算法在二元化的特征选择问题中表现出优异的效果。
2.7 评价指标
本文用到的评价指标有检测精度(Accuracy)、检测率(True Positive Rate)、F1 值。 以上评价指标都是基于混淆矩阵中4 个度量来计算的。 混淆矩阵中,TP 表示实际为正预测为正的样本,TN 表示实际为负预测为负的样本,FN 表示实际为正预测为负的样本,FP 表示实际为负预测为负的样本。 Accuracy 表示正确分类的样本数占所有样本数的百分比,常用于表征算法检测能力的指标。 检测精度定义如下。

检测率(True Positive Rate,TPR)是指被检测出的正样本占全部正样本的比例,检测率越高表明算法检测性能越好。 检测率定义如下:

F1 值指标综合了Precision 与Recall 的结果。F1 值的取值范围为0~1,1 代表模型的输出最好,0 代表模型的输出结果最差,其定义如下:

其中,precision 和recall 是另外两个度量,其计算公式如下:

3 仿真实验
本节将介绍PIO 特征选择算法评估KDDCUP99 数据集。 该算法与目前常用的一些特征选择算法(如遗传算法、粒子群算法、蝙蝠算法等)进行了比较。 所有的特征选择算法都使用Python 中scikit-learn 库中的决策树分类器进行建模与评估。
所有被检测的算法都进行了TPR、FPR、F1 值和准确率的评估。表1 给出的是一系列其他算法所选择的特征。 使用决策树对每个用于特征选择的算法进行评估,只使用指定的特征对模型进行训练,然后使用测试集对模型进行评估。所有的模型都使用相同的方法在相同的数据集上进行训练,以确保比较的公平性。的收敛速度慢于CPIO;在第60 次迭代时,解的质量停止 提 高。 从 图 中 结 果 来 看,CPIO 比SPIO 更 有 效。 余 弦 相似度法用于PIO 的离散化,比传统方法收敛速度快得多。CPIO 所采用的新鸽群优化算法有助于算法不断增强解的稳定性,并很容易地跳过算法的局部最优解。
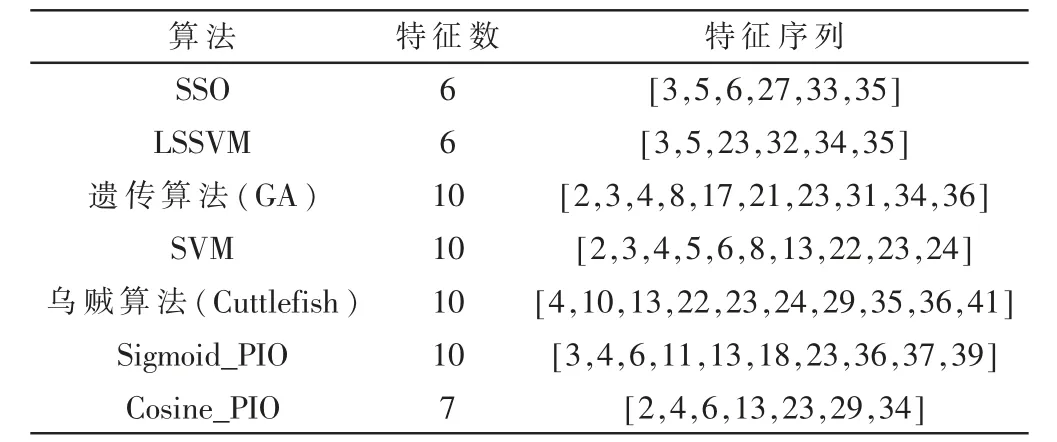
表1 KDDCUP99 特征选择的结果

图4 SPIO 和CPIO 的收敛曲线
图5 展示了在KDDCUP99 上测试的7 种算法的TPR结果和准确性。 每个柱表示相应测试算法30 次运行的评分结果均值。从图中可以看出,所提出的CPIO 算法相对于其他所有经过检验的算法具有最高的精度。结果表明,在相同的迭代次数下,CPIO 在TPR 和精度方面都优于SPIO。 使用Cuttlefifish 算法训练的模型在准确性方面的结果最差。从图5 可以看出,TPR 高、准确率低的算法在适应度函数中没有考虑误报率。

图5 几种算法的TPR 和准确率
F1 值比其他度量具有更好的总结和指示作用,因为它是综合了精确率和召回率的度量。图6 显示了所有检测算法的F1 值结果。 由图可见,CPIO 的F1 值最高。
影响特征选择算法质量的另一个度量方法是选择特征的数量。 特征的数量影响模型的构建和测试时间。图7 展示了3 种情况下的构建和测试时间:使用数据集中的所有特征(41 个特征)、使用SPIO 选择的10 个特征、使用CPIO 选择的7 个特征。结果表明,特征的数量影响了模型构建和测试所需的时间。

图6 KDDCUP99 上集中算法的F1 值

图7 KDDCUP99 训练和测试的时间
4 结论
本文提出了一种基于鸽子优化算法的入侵检测系统特征选择算法。 提出的PIO 特征选择旨在减少构建健壮的IDS 所需的特征数量,同时保持较高的检测率、准确性和较低的误报。 提出的PIO 特征选择算法将KDDCUPP99、特征数量分别从41 个减少到7 个。 该方法保持了较高的TPR 和精度,大大减少了建模所需的时间。
特征选择是一个离散优化问题。 对于连续的群体智能优化算法,必须采用离散化处理算法来解决这样的问题。 提出了一种基于余弦相似度的连续算法离散化方法,并与传统离散化方法进行了比较。 在相同迭代次数下,该离散化方法比传统方法收敛速度快。

