涂层织物类膜材的偏轴梯形撕裂行为
张旭波,吴明儿,包 晗
(同济大学 建筑工程系,上海 200092)
膜结构自重轻、形态丰富,可广泛应用于体育设施、会展中心等大型空间结构.然而因强风、大雪等因素引起的膜结构破坏现象时有发生,它们绝大部分是因膜材的局部撕裂扩展为整体破坏而引起的[1-3].
目前国内外膜结构技术规范均按照膜材的抗拉强度进行强度验算[4-7],其撕裂强度仅作为膜材的一项性能参数.膜材的撕裂强度测试方法有舌形撕裂法、梯形撕裂法和中心撕裂法等[8].现阶段,膜材撕裂性能的研究方法主要为中心撕裂法[9-13],该方法与膜结构实际撕裂破坏过程更为接近,但还未被各国规范广泛采纳;梯形撕裂法的破坏模式单纯、数据稳定,为目前国内外膜结构相关规范采用最多的方法[4,6-7].关于织物梯形撕裂的研究主要包含撕裂影响因素分析、撕裂强度预测及有限元仿真.Hager等[14]研究了机织物的梯形撕裂破坏,指出梯形撕裂强度取决于纱线断裂伸长率、纱线破断力和织物组织等因素;黄时建等[15]研究了聚氨酯涂层性能与织物梯形撕裂强度的关系,发现涂层工艺参数会改变织物的模量、拉伸强力及断裂伸长率,进而影响织物的撕裂强度.Steele等[16]推导了梯形撕裂下织物在切缝处第1根纱线断裂时的撕裂强度预测公式;储才元等[17]分析了有/无涂层织物的梯形撕裂性能,得到织物的最大撕裂强度预测公式.Wang等[18]推导了包含两向纱线及涂层贡献的梯形撕裂强度预测公式,并与试验结果进行了对比分析.Wang等[19]用有限元法模拟了有/无涂层织物的梯形撕裂过程,并分析了撕裂强度的影响因素.
已有文献多基于标准梯形,即预制切缝沿着经、纬向扩展进行撕裂试验;而对于偏轴梯形,即纱线与切缝间存在夹角的撕裂试验研究甚少[20].但在实际结构中,膜材的初始裂缝与经、纬向大多数成一定夹角.偏轴梯形撕裂试验将偏轴角(θ),即切缝与纱线间的夹角作为试验参数,相较标准梯形撕裂,偏轴梯形撕裂与膜结构的真实撕裂情况更为接近.因此,本文对6种涂层织物类膜材进行偏轴梯形撕裂试验,得到各类膜材在不同偏轴角下的撕裂强度及撕裂强度随偏轴角变化的规律,分析了撕裂机理,并采用有限元法(FEM)对偏轴梯形的撕裂起始段进行模拟.
1 试验
1.1 试验材料
6种涂层织物类膜材包括2种PVC(聚氯乙烯)涂层平织聚酯纤维膜材、1种PVC涂层经编聚酯纤维膜材、2种PVC涂层玻璃纤维膜材和1种PTFE(聚四氟乙烯)涂层玻璃纤维膜材.其中,基布为聚酯纤维的膜材简称为P类膜材,基布为玻璃纤维的膜材简称为G类膜材.各膜材的基本参数如表1所示.需要说明的是,表1中的抗拉强度和断裂伸长率为每类膜材经、纬向各5个试样进行单轴拉伸试验得到的平均值.
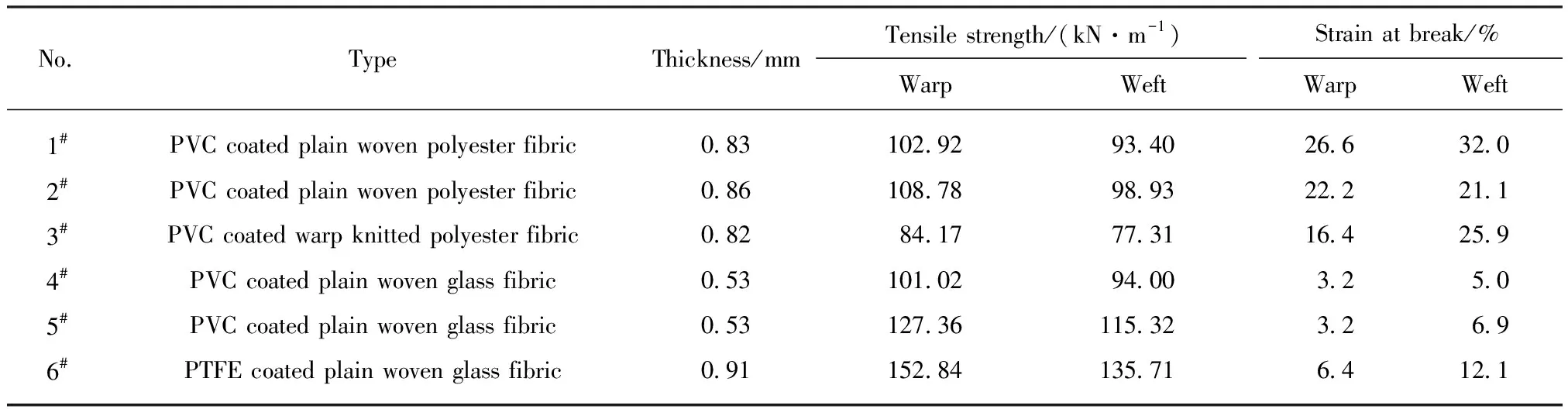
表1 膜材基本参数
1.2 试验设备及试验环境
试验设备为深圳新三思CMT4204微机控制电子万能试验机(量程20kN);夹具为平面夹持式夹具.万能试验机和夹具如图1所示.参考GB/T 6529—2008《纺织品 调湿和试验用标准大气》,将试验环境设为(20±2)℃、相对湿度(65±4)%、1个标准大气压(101.325kPa).
1.3 试验方案
依据检测规程要求制作试样,试样尺寸如图2[6]所示.试验采用加载速率为100mm/min的等速加载,隔距长度为(50±1)mm.试验变量为偏轴角θ(切缝与经向的夹角),取值范围为0°~90.0°,以相差7.5°为1组,共13组.对于膜材1#、3#、5#及6#,其各偏轴角均制备5片试样,以保证试验数据的有效性;对于膜材2#、4#,由于其与膜材1#、5#性质相近,故各偏轴角仅制备3片试样.

图1 万能试验机及夹具Fig.1 Equipment and fixture for test
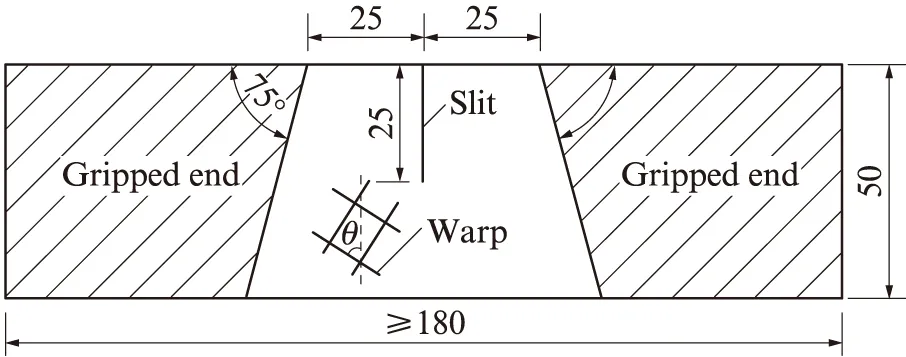
图2 试样尺寸Fig.2 Dimension of specimen(size:mm)
2 试验结果及分析
2.1 试验过程
偏轴梯形撕裂几何模型见图3,其中细实线表示经、纬向纱线.
偏轴梯形的典型撕裂过程如图4所示.由图4可见:在拉伸载荷作用下,试样中预制切缝根部的经、纬向纱线率先承载,并出现伸长变形;随着荷载的增加,根部变形最先达到断裂伸长率的纱线首先发生断裂,斜向裂缝开始形成;随后,撕裂三角区内不断有纱线断裂,又不断有新的纱线承载,三角区逐渐移动,斜向裂缝逐渐扩展;最终,由于三角区中已没有足够的纱线继续承载,撕裂强力逐渐变小,直到破坏,最后几根承载的纱线仅被夹具的一端夹头夹持,涂层及另一方向上的纱线无法提供足够约束力,通常被抽拔出来.
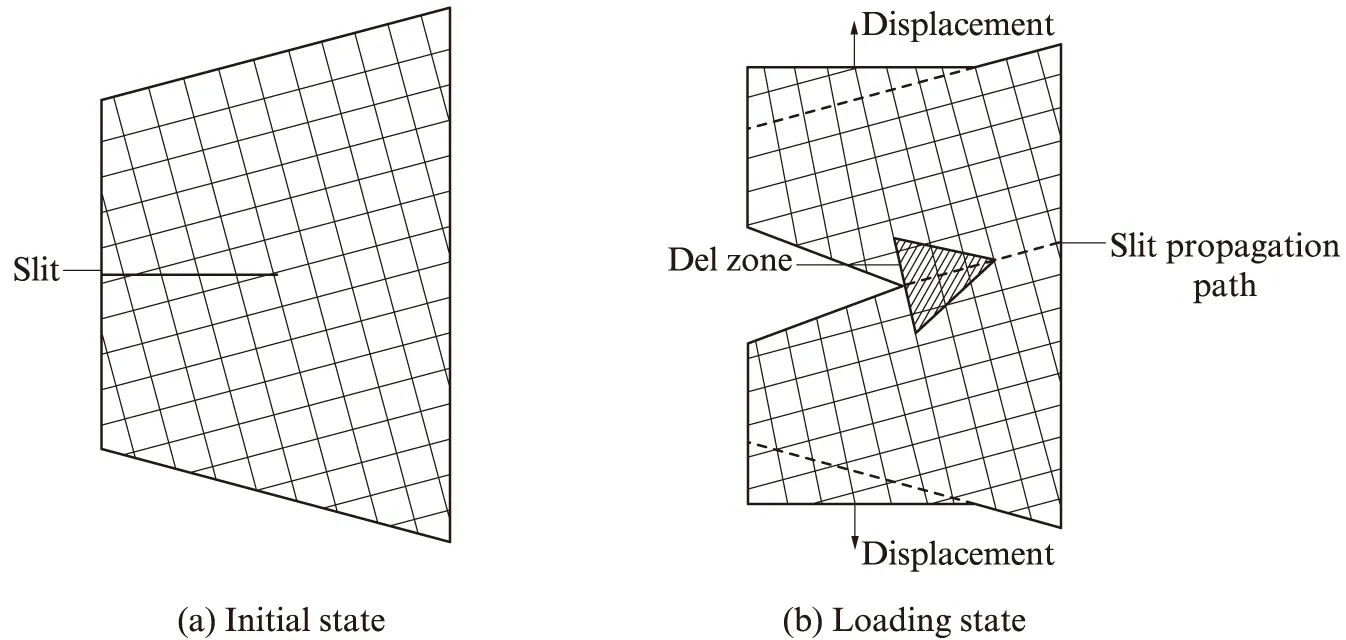
图3 偏轴梯形撕裂的几何模型Fig.3 Geometrical model of off-axial trapezoid tearing

图4 偏轴梯形的典型撕裂过程Fig.4 Typical tearing process of off-axial trapezoid tearing
2.2 试验结果
依据检测规程相关内容,将各类膜材试样在各偏轴角下所有试样5峰均值的平均值作为该偏轴角的撕裂强度[6].为比较相同纤维类型的膜材,采用膜材单位厚度的撕裂强度,得到各类膜材在不同角度下的撕裂强度,如图5所示.由图5可以看出:(1)各类膜材的撕裂强度随角度的变化大致以45.0°为对称轴,0°~45.0°及90.0°~45.0°撕裂强度先减后增;最大值位于45.0°;最小值位于15.0°或22.5°、75.0°或67.5°,该值为标准试样(0°和90°试样)撕裂强度的85%~95%.(2)与基布为玻璃纤维的膜材4#、5#、6#相比,基布为聚酯纤维的膜材1#、2#、3#在各角度下的撕裂强度更大;相同纤维类型下,膜材断裂伸长率较大的膜材3#和6#的45.0°偏轴撕裂强度更大.
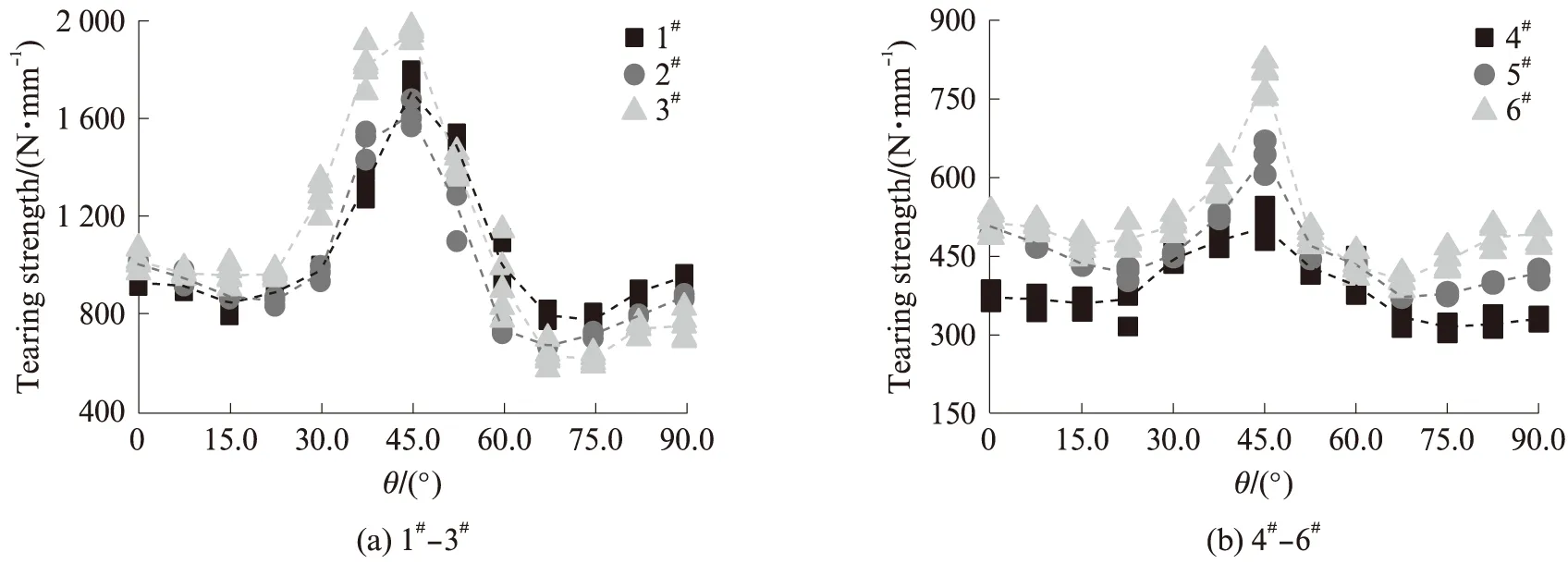
图5 各类膜材在不同偏轴角下的撕裂强度Fig.5 Tearing strength of different materials at different off-axis angles
撕裂口始终沿着经向或纬向发展.当切缝与经向夹角小于等于37.5°时,纬纱断裂,裂缝沿经向扩展;当切缝与经向夹角大于等于52.5°时,经纱断裂,裂缝沿纬向扩展;当切缝与经向夹角为45.0°时,裂缝沿经向或者纬向扩展.以膜材4#为例,其在不同偏轴角下的破坏形态如图6所示.
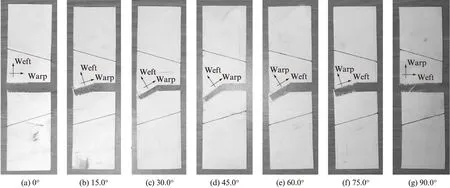
图6 膜材4#在各偏轴角下的破坏形态Fig.6 Failure mode of material 4# at different off-axis angles
2.3 试验结果分析
图7~9为不同偏轴角试样的纱线分布、不同膜材在不同偏轴角下的荷载-位移曲线、不同膜材在不同偏轴角下撕裂起始时的变形图.
2.3.1偏轴角为0°/90.0°
偏轴角为0°/90.0°试样为标准试样,其承力纱线两端均被夹持(见图7(a)).限于篇幅且便于展示,P类和G类膜材的90.0°试样荷载-位移曲线(见图8(a))仅画出了膜材1#和膜材5#的结果,其中“▲”表示撕裂起始点,括号内为起始点具体的位移、荷载数据.由图9(a)、(d)可以看出,G类膜材虽然强度较高,但其断裂伸长率远小于P类膜材,撕裂时形成的撕裂三角区小,故其撕裂强度、撕裂起始位移及产生的变形均小于P类膜材.由此可知,膜材的梯形撕裂强度由膜材强度和断裂伸长率共同决定.
2.3.2偏轴角为15.0°/75.0°或22.5°/67.5°
偏轴角为15.0°/75.0°或22.5°/67.5°试样的撕裂强度最小,其纱线分布情况为两端夹持纱线和一端夹持纱线并存(见图7(b)).对比图8(a)、(b),图9(a)、(b)及图9(d)、(e)可知,该种情况下试样的荷载-位移曲线及变形情况与90.0°情况相近,但膜材荷载-位移曲线后续峰值与初始峰值差别不大,且逐渐降低,因此其5峰均值更小.
与0°/90.0°情况相同,由于膜材强度和断裂伸长率的共同影响,15.0°/75.0°或22.5°/67.5°情况下P类膜材的撕裂强度、撕裂起始位移及产生的变形均大于G类膜材.由图8(a)、(b)可知,该种情况下膜材撕裂起始强度及位移与90.0°情况相当,原因在于撕裂起始时2种情况的切缝尖端纱线夹持情况(均为两端夹持)与形成的三角区相近.
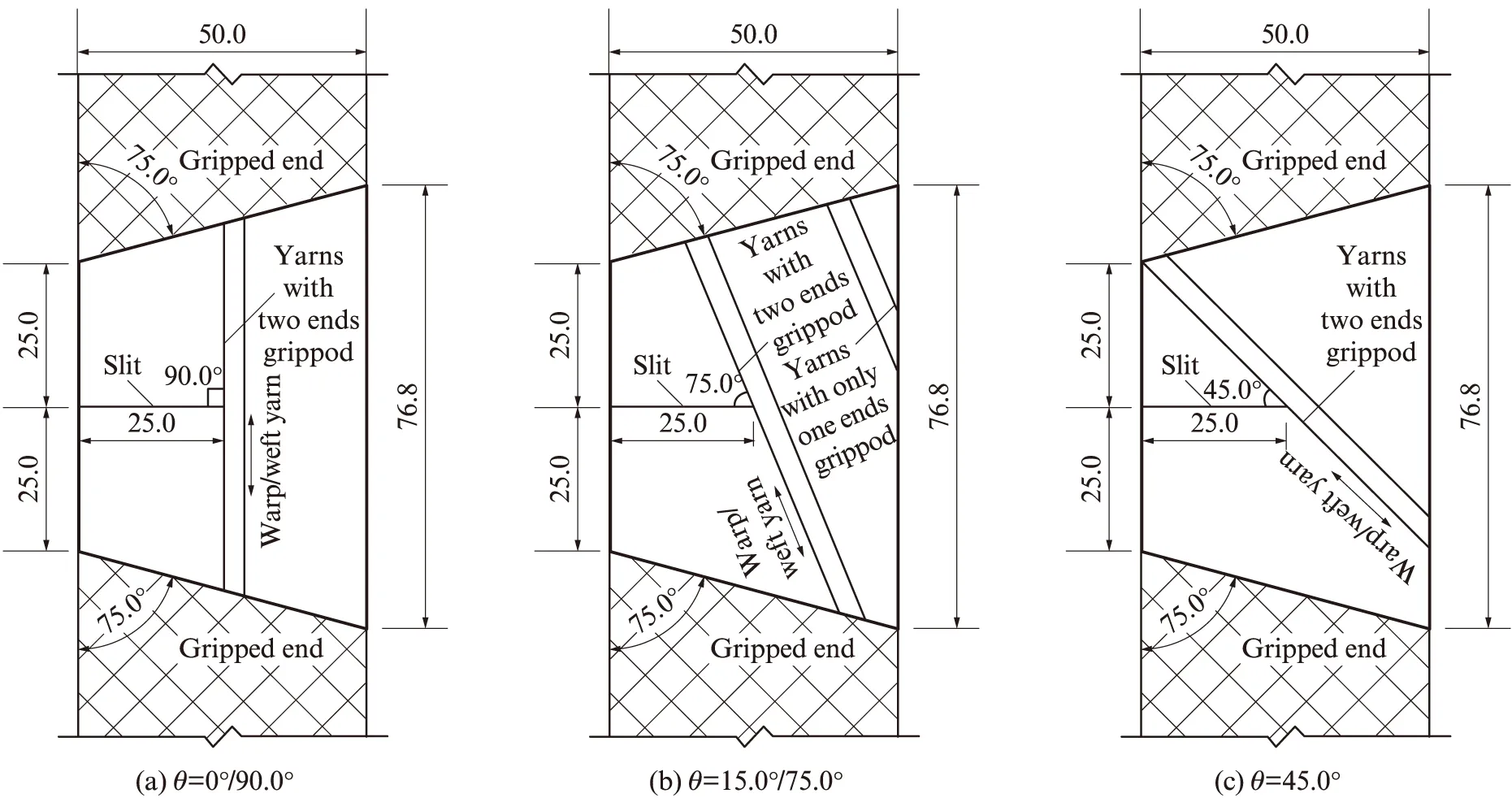
图7 不同偏轴角试样的纱线分布Fig.7 Distribution of yarns at different off-axial angles(size:mm)
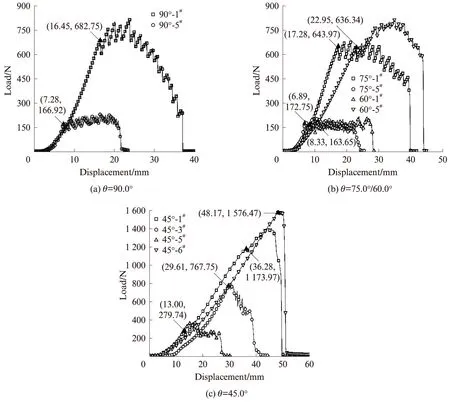
图8 不同膜材在不同偏轴角下的荷载-位移曲线Fig.8 Load-displacement curves of different materials at different off-axial angle
2.3.3偏轴角为45.0°
45.0°试样的纱线仅有一端被夹持(见图7(c)).对比图8(a)、(c),图9(a)、(c)及图9(d)、(f)可以看出,同种膜材的45.0°试样撕裂起始时的位移、强度及变形均大于90.0°试样,且距离切缝尖端较远的纱线明显参与受力.这表明一端夹持纱线在未被抽拔时可通过自身变形来调整受力,纱线上的力分布更均匀,变形更充分;预制切缝根部的集中应力被分散至远端纱线,进而承受更大的荷载.
与0°/90.0°的情况类似,45.0°情况下G类膜材的撕裂强度、撕裂起始位移及产生的变形均小于P类膜材;同时,相同基布类型的膜材断裂伸长率越大,其45.0°试样撕裂强度及变形也越大.
结合图8、9可知,当偏轴角由75.0°向45.0°变化时,膜材变形逐渐充分,荷载-曲线初始段刚度减小,5峰均值增加;但由于纱线约束形式的改变及一端夹持纱线调整受力的作用,纱线由单根纱承受较大荷载发生断裂变为多根纱线共同承受较大荷载,膜材发生明显的整体变形,且荷载-位移曲线的峰值数目减少.
3 偏轴梯形撕裂有限元分析
采用Abaqus软件中的显式算法对偏轴梯形撕裂进行有限元分析.选用三节点三角形薄壳单元,对切缝尖端处网格进行加密.计算过程中通过调整网格密度和显式计算时间步长,保证计算的收敛性及结果的稳定性.从试样装配到加载的全过程模拟如下:(1)装配过程 将梯形的2个斜边作为铰节固定边界,对固定边界施加绕钝角角点的转动,强制位移至边界成水平状态(见图10(a)、(b)).(2)加载过程 装配结束后,对梯形的2个斜边施加方向相反的竖向位移(见图10(b)、(c)).另外,考虑涂层织物各向异性及非线性的材料特点,采用Abaqus中提供的纤维材料模型近似处理织物经纬向的非线性.该模型可考虑经、纬向纤维不同的力学性能,通过输入经、纬向纤维非线性应力-应变关系考虑材料的各向异性以及非线性特性,常用在织物材料力学行为的模拟.但该模型忽略了经、纬向纤维的相互作用.本文将膜材视为各向异性的非线性弹性材料,将经纬向单轴拉伸应力-应变曲线作为纤维材料模型参数进行撕裂过程的分析.该种处理方式考虑了涂层对参与受力的贡献,但忽略了涂层对经纬向传力的影响.本文仅列出膜材1#的撕裂过程进行分析结果.图11为计算中采用的应力-应变曲线.

图9 不同膜材在不同偏轴角下撕裂起始时的变形Fig.9 Deformation of different material at different off-axial angles

图10 0°试样的装配及加载过程Fig.10 Assembly and loading process of material at 0°
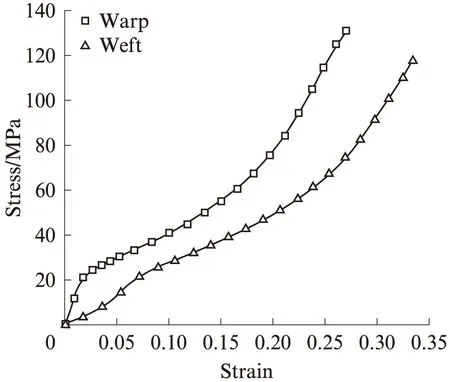
图11 膜材1#经纬向单轴拉伸应力-应变曲线Fig.11 Strain-stress curves of material 1# along warp and weft
采用一般的有限元方法计算带切缝模型时,无法规避切缝尖端的奇异性,仅能计算至撕裂起始点.因此,除对切缝尖端网格进行加密外,本文仅进行加载至撕裂起始点的有限元计算,并以距离切缝尖端1条纱线间距处的应变值达到由单轴拉伸试验得到的膜材断裂伸长率值作为撕裂起始的判断依据.引入该撕裂起始判据后,各偏轴角下试验与有限元法得到的撕裂起始荷载如图12所示.试验与有限元模拟的荷载-位移曲线对比如图13所示,其中“▲”表示撕裂起始点.由图12、13可知:有限元模拟结果与试验结果吻合较好;当偏轴角从0°向45.0°变化时,由于膜材抗剪能力较小,故变形增加,荷载-位移曲线斜率减小.90.0°向45.0°变化过程与此同理,仅仅是发生断裂的纱线有所不同.
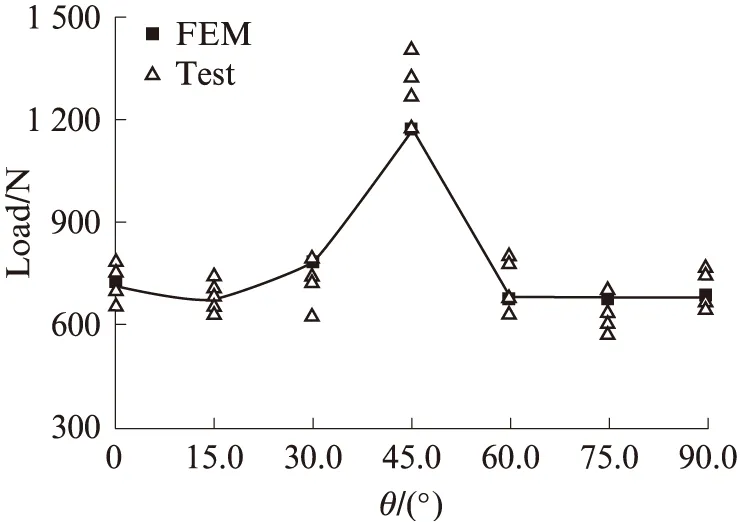
图12 试验及有限元得到的撕裂起始荷载Fig.12 Initial loads of tearing obtained by tests and FEM
图14为撕裂起始时0°、30.0°、45.0°试样膜面的经纬向正应变和剪切应变云图.由图14中的剪切应变云图可以看出:当偏轴角从0°向45.0°变化时,整体膜面剪应变的贡献增加;切缝尖端的集中应变被分散,尖端沿纬向的正应变分布更加均匀,试样进而承受了更大的荷载.
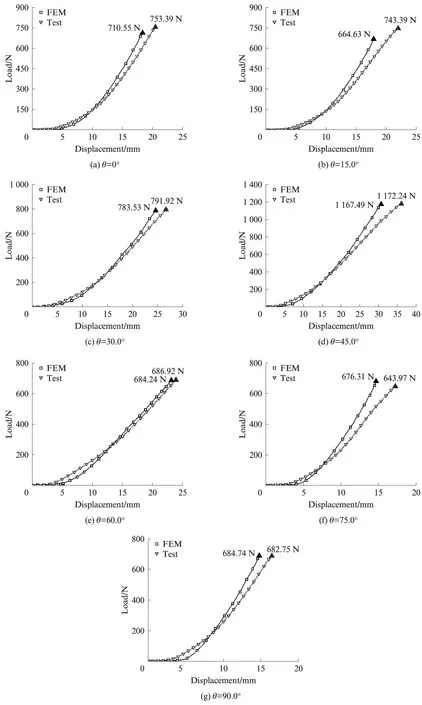
图13 膜材1#撕裂起始前的荷载-位移曲线Fig.13 Load-displacement curves of material 1# before tearing
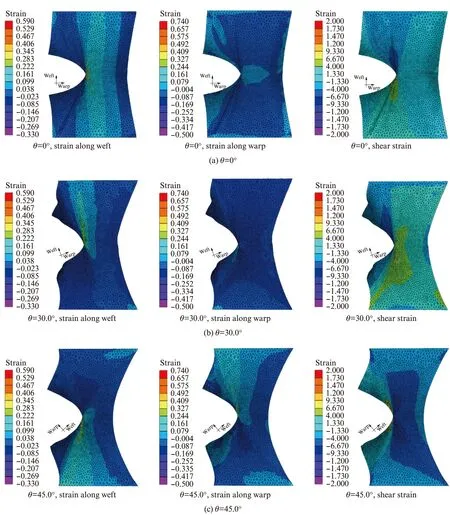
图14 0°、30.0°和45.0°经纬向正应变和剪切应变云图Fig.14 Strain along warp/weft and shear strain at 0°,30.0°,45.0°
4 结论
(1)在偏轴梯形撕裂试验中,各类膜材撕裂强度与偏轴角曲线近似以45.0°轴对称,0~45.0°及90.0°~45.0°撕裂强度呈先减后增趋势;撕裂强度最高点位于45.0°;最低点位于15.0°或22.5°、75.0°或67.5°.最小撕裂强度为标准试样撕裂强度的85%~95%.膜材在0~37.5°发生纬向断裂,裂缝沿经向扩展;在52.5°~90.0°发生经向断裂,裂缝沿纬向扩展;在45.0°沿经向或者纬向扩展.
(2)各类膜材的偏轴梯形撕裂强度由纱线的抗拉强度和断裂伸长率共同决定.相同偏轴角下,P类膜材的撕裂强度比G类大;膜材相同时,45.0°试样发生撕裂时的强度和变形比其他角度大.
(3)采用Abaqus软件对不同偏轴角下撕裂试验进行有限元分析,其模拟结果与试验结果吻合较好,二者得到的撕裂起始荷载较为接近.

