相似性聚类在直升机传动轴健康管理中的研究
侯学理, 李 凯, 车 力, 马晓聪, 侯旭鹏
(1.中国人民解放军95579部队,四川 成都 611531; 2.空装驻西安地区第九军代室,陕西 西安 710002;3.中国人民解放军61213部队,山西 临汾 041000)
直升机因其具有优越的垂直起降、灵活的机动性等特点在军事和民用都有广泛的应用,而且伴随我国低空领域对民用的开放,将迎来直升机发展的黄金时代。同时,其安全性能也越来受到人们的关注。
直升机的三大关键部件为:动力系统、传动系统和操纵系统。直升机动力系统一般采取双发或者辅助设备,操纵系统采用液压、机械等两套以上的系统补充。而传动系统需要保证传递效率和传递方向,一般采取单向传递,无可用替代系统。所以在直升机三大系统中传动系统安全余度最小。直升机传动系统示意图如图1所示。
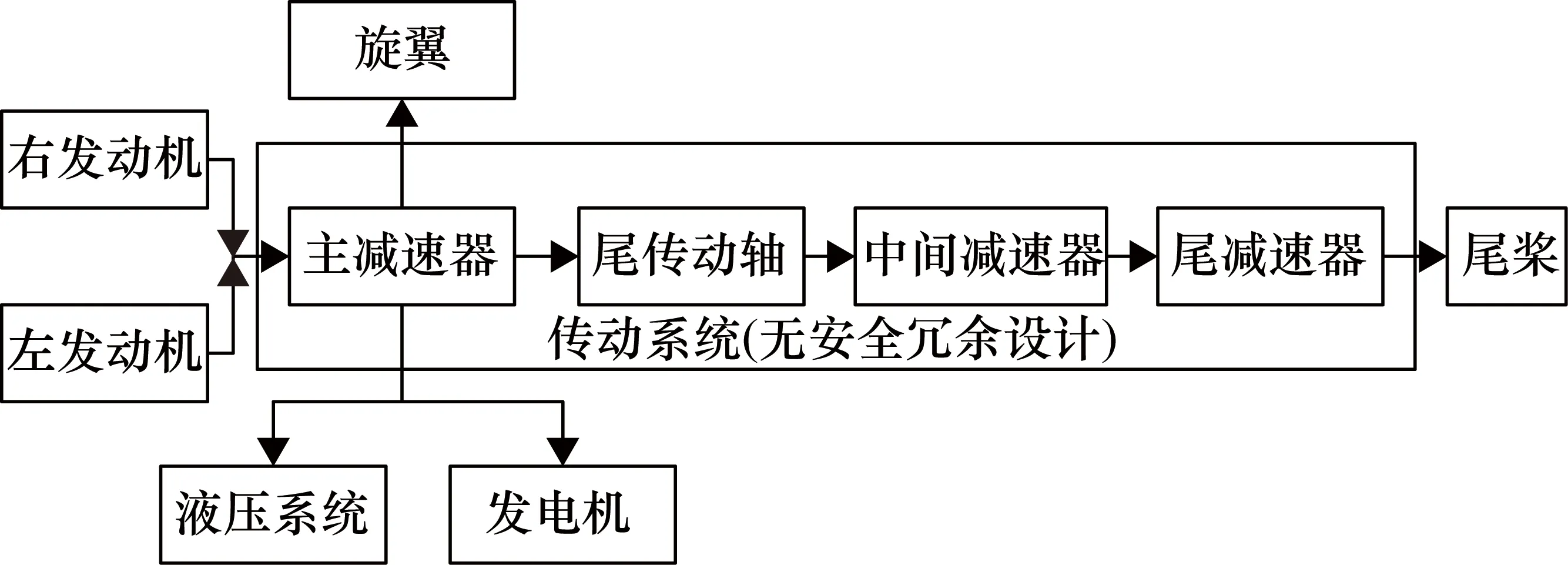
图1 直升机传动系统示意图
直升机传动系统的作用是将发动机输出的功率按照一定的比例传递给旋翼和尾桨,并按各自的需求降低转速带动其旋转,使直升机起飞和平衡。一旦传动系统被破坏(特别是尾传动轴)或出现故障,动力将无法传递到尾桨,直升机将无法航行。传动系统的性能直接影响直升机的总体性能,关系到直升机的飞行安全和稳定[1]。美国空军后勤保障部门就直升机的维护数据表明,在直升机机械故障引发的飞行事故中,由传动系统和动力系统造成的事故占比高达68%,维修费用也占到了总维修费用的58%[2]。贡慧等[3]、张娟等[4]对2016年以前的世界直升机发生的事故原因、事故机型、主要事故系统进行了统计分析,发现传动(动力)系统是引发直升机事故的一大诱因,占所有直升机飞行事故的15.9%。这也从另一方面说明传动系统是直升机的核心关键部件之一,其可靠性水平在很大程度上决定了直升机的安全性。
然而目前我国的直升机传动系统的研究,特别是传动轴的研究,还都停留在对信号分析的研究方面,如湖南大学研发了直升机传动系统故障诊断软件;南昌航空大学对传动系统振动信号分析进行故障研究,空军工程大学、国防科技大学等院校也都在研究直升机传动系统故障,但这些故障诊断方法基本上都是基于传统的信号分析,不仅需要大量的信号分析专业领域的专家还需要有经验丰富的故障诊断专家,在实际工程中很难实现,而且实现后需要依靠人来进行判断。
目前人工智能和数据挖掘技术均已成熟,这就使用新技术解决传统问题成为可能。而且最主要的原因是数据挖掘技术更多的是依赖于数据最原始的信息,减少了过程中对人的依赖和人为因素。同时,未来的航空业将向数字航空、智能航空发展,原来的方法将很难适应未来的数字航空、智能航空。
目前国外的大多数战斗机均已安装了健康管理系统(PHM),在直升机上也使用了健康与使用监控系统HUMS(Health and Usage Monitoring System),我国也在进行该项研究,这些研究绝大部分都依赖于数据分析或者数据挖掘技术。数据挖掘前期必须要对数据进行处理,例如数据降维、数据清洗等。只有前期数据处理得好,后期数据分析才能准确。目前国内几所高校均在研究用数据处理的方法进行故障诊断,但是将数据挖掘技术用在直升机传动轴上的健康管理研究还处于起步阶段。
本文提出了一种改进后的相似性聚类(Affinity Propagation,AP)方法并应用于传动轴上的故障特征提取。通过实验验证该方法可以进行故障特征提取和分类。并与成分分析法(Principal Component Analysis,PCA)对比,改进后的相似性聚类方法优于成分分析法。
1 相似性传播聚类(AP)算法的研究
1.1 传统AP算法
相似性传播聚类算法[5]是通过在原始数据集中识别最具有代表性的子集来进行数据分类的无监督学习算法[6]。相似性聚类的核心思想利用数据信息之间相互不断的传递,最终得到一个能够描述这个数据集合的中心子集,从而使得每个数据点归于一类,最终将数据集分为几个部分[7]。
设输入X1,X2,…,Xn为n个d维实数向量样本Xi={xi1,xi2,…,xid},i=1,2,…,n,则d为数据样本Xi的特征维度数,则样本数据集可以表示为X=[X1,X2,…,Xn]T,即
(1)
输出为通过最后的聚类得到的表示点与点之间的关系矩阵ci,j(i,j=1,2,…,n)。
① 若ci,j=1,判定点xj为点xi的中心;
② 若ci,j=0,判定点xj不是点xi的中心。
相似性传播算法目标要使数据和它的中心点之间的相似性最大,即中心点能表示该数据集合的某一特征。通过最大和算法理论算法[8]求解ci,j,使xj成为xi中心的可能性最大,具体算法如下。
为了求解ci,j,必须将所有局部函数联合起来,建立一个全局目标函数,这样解出来的结果才是全局最优解。
设目标函数S(c1,1,c1,2,…,cn,n),为了满足算法实际需求,求解S(cij)还需几个修真目标函数。
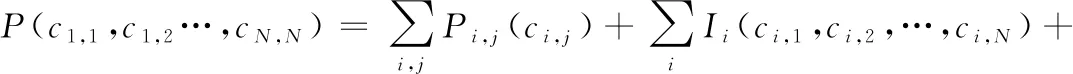
(2)
式中,Ii(cij)和Ej(cij)为约束函数,用于修正目标函数S(cij)。
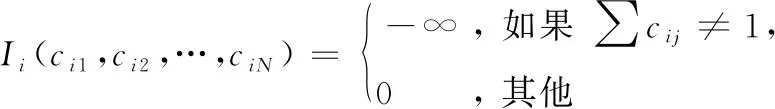
(3)
Ej(c1j,c2j,…,cNj)=
(4)
式(2)表示当ci,j=1时,点xi是属于点以xj为中心的集合。式子(3)、式(4)表示每一个数据点只能属于一个中心点集合。利用最大和信息更新原则,推出图2所示的相似性传播聚类算法示意图来计算ci,j。
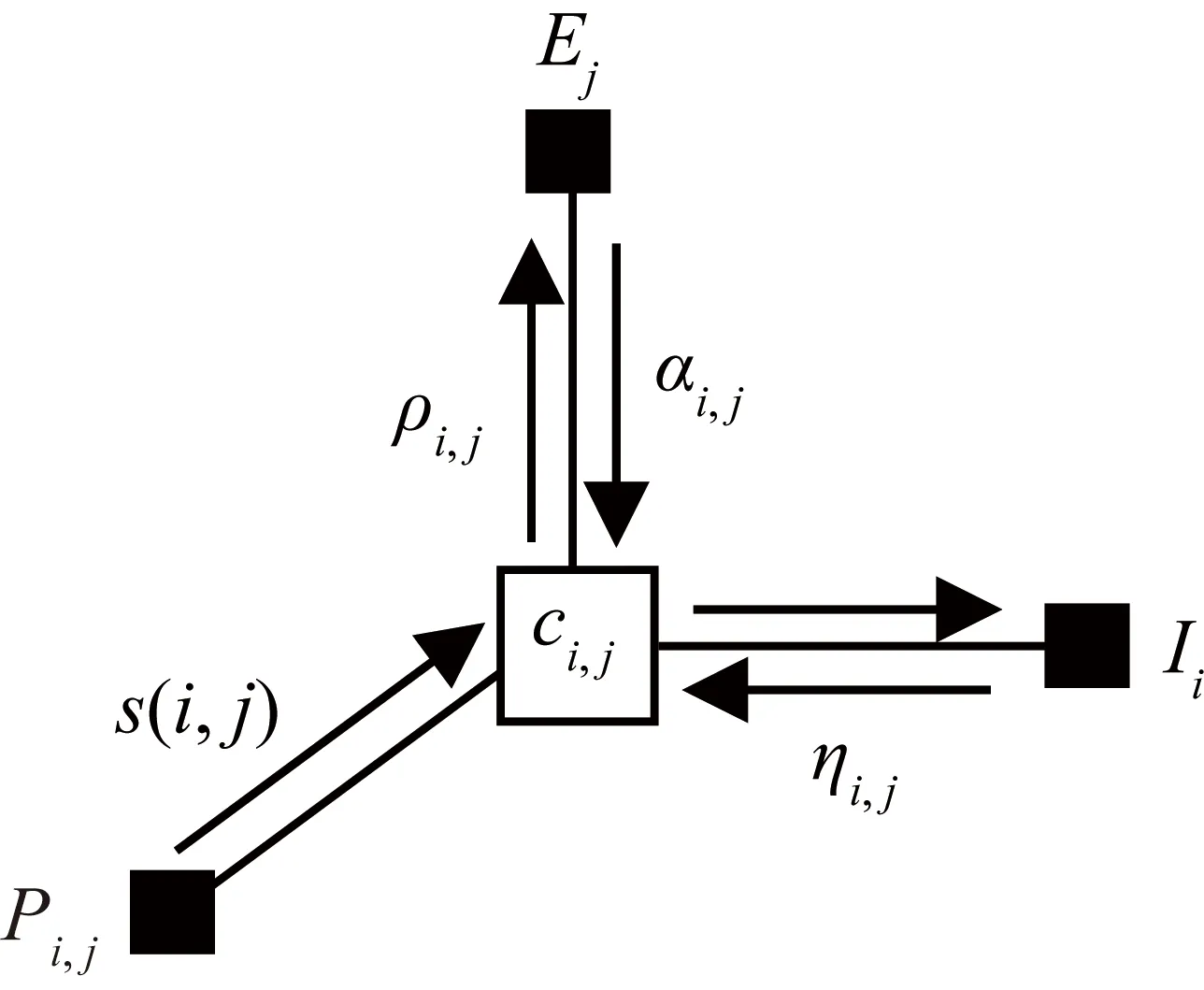
图2 相似性传播聚类算法示意图
利用最大和原则:
(5)
此外,在计算ci,j时包括s(i,j)在内的5个信息需要通过不断的迭代更新。
βi,j=s(i,j)+αi,j
(6)
(7)
(8)
(9)
式中,ρi,j为责任信息,传递是从点xi到点xj的信息,表示点xj作为点xi的集合的中心点的合适程度;αi,j为可用信息,表示xj在已经从其他数据点上获得可用信息的前提下,作为xi中心的可能性的大小;βi,j和ηi,j为计算过程中间变量。计算数次迭代之后,求解使得ρi,j+αi,j最大和所对应的ci,j矩阵。在实际应用这个算法的时候,很多时候只需要输入表示数据之间距离的相似矩阵s(i,j)。
传统研究表征距离的函数有欧氏距离、曼哈顿距离、明可夫斯基距离、切比雪夫距离等。现在又有学者提出了改进的表征距离的Hsim(X,Y)、Close(X,Y)[9],以及改进的高维数据相似性度量函数Esim(X,Y)[10]。这些改进的函数使相似性传播聚类的降维能力有了很大的提高。而本文研究的直升机传动系统的数据维度并不是很高,而且需要较快的时间计算能力,所以选择负欧式距离。
s(i,j)=-‖xj-xi‖2
(10)
1.2 改进AP算法
式(10)选取某时刻某两个特征向量之间的欧氏距离平方和。其优点是放大了数据之间大的差异,但缺点是对数据之间细小的差异不明显,这就使得两个数据之间差别大的时候分类很清楚,数据差异小的时候分类不理想,甚至可能导致分不清楚。特别是中心点的选取可能效果更差。
为了解决这个弊端,提出一种加权的欧式距离:
(11)
式中,αjt为每个特征的权重用于衡量Xi在t时刻这个数据在整个测量数据序列中的影响程度,目的是使得AP聚类的聚类效果更好。αit的具体求解如下:
(12)
(13)
(14)
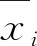
式(11)中αit为给每一个测量数据的每一个维度都进行了标记,表示在第t个的i维的重要程度的大小,从而使数据纬度之间的差异变大,将会使重要的维度在整个维度序列中表现出来,在算法上将比较清楚地表征出其所代表的特征与其他的值的差异,使聚类原始数据的差异性变大,但又不会失去数据的本来特性。
式(11)能表示出每个数据的每个特征的重要程度,重要的特征αit大,能在整个数据维度里面更加凸显,所以理论上可以使分类效果更好。
2 直升机传动故障特征定义
目前,先进直升机对重要的关键系统都做了监控。通过采集来的信号记录和显示设备运行情况,应用最多的是时域信号,时域信号是监测设备直接测量到的信号,包含的信息量大且易于观察和理解[11]。但应用数据挖掘的方法来处理、识别直升机传动系统的故障时,需要对采集到的信号进行重新定义[12]。对于时域信号分析而言,常用的特征有最大值、最小值、有效值、均值、均方值、方差、标准差、峰值、峰-峰值[13]等一批有量纲的指标。具体如表1所示。

表1 故障特征定义表
上述这些有量纲的指标一般受工况、负载、环境、转速等外界条件的变化影响较大,给工程应用和研究增加了难度。但可以通过它们演变出一些无量纲指标,如峭度(Kurtosis,K)、偏斜度(Skewness,S)、波形指标(Shape Factor,SF)、脉冲指标(Impulse Factor,IF)、峰值指标(Crest Factor,CF)和裕度指标(Clearance Factor,CLF)[14]等,以及在时频域分析中频率峰值均值比和频域均方根等一些参数指标。这些都是从某一方面来描述传动轴的特性[15]。这些指标的具体公式和含义在其他文献中有详细的描述这里不再赘述。
这些时域的有量纲的特征和无量纲的特征以及频域、时频域都可以作为故障数据的特征,均可以参与故障特征的提取,而且时域、频域、时频域是可以相互转化和进行分析的。本文为了简化计算量并说明该方法有效性选取了时域的特征进行分析。
3 直升机传动轴的故障特征选择方案
通过前面的介绍可知,改进后的AP算法可以更好地描述数据之间的差异,能使数据之间的不同特点表现得更加明显。故这种改进后的方法可以判别更加细微的差异,故该方法对直升机传动轴故障早期的相似故障有很好的判别能力。应用改进后的AP算法进行传动轴故障特征选择,具体如下。
改进AP算法故障特征选择流程图如图3所示。
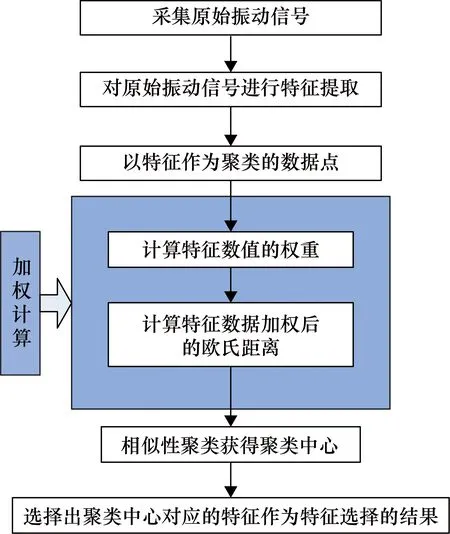
图3 改进AP算法故障特征选择流程图
① 首先对采集到的原始信号进行整理,使其成为一个信号序列Xt={X1,X2,…,XT},T为信号序列的长度。
② 根据前面第2节定义的有量纲和无量纲的多个特征,将每一个特征作为一个维度对原始信号序列Xd进行维度计算。设信号序列Xd计算的维度为d=1,2,…,D,D为维度长度,则可将信号序列表示为Xd={X1d,X2d,…,XTd}。
③ 为了便于相似性聚类算法计算,将X进行转置得到信号的转置特征序列Xt={X1t,X2t,…,XDt},d=1,2,…,D,t=1,2,…,T,则输入序列变为
(15)
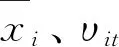
⑤ 计算欧式距离:计算特征序列XDT中每个数据点Xdi与特征序列XDT中对应的数据点Xjt之间加权后的欧式距离s(i,j)′dt。
(16)
⑥ 将式(16)代入式(2)、式(3)、式(4)中,计算出每个特征的归属类,从而找出哪些特征是所有数据点的特征中心,并删除冗余的特征数据。
4 实验验证
故障的特征提取是故障诊断的关键步骤,该步骤直接影响后面的故障诊断。在实际的故障诊断问题中,首先利用表1中的有量纲指标以及其他的无量纲指标和频域上的特征指标,分别计算出来数据点的特征,这些均值、均方值、有效值、方差、标准差、峰值、峰-峰值、峭度、偏斜度、波形指标、脉冲指标、峰值指标、裕度指标、频率峰值均值比、频域均方根等都是描述这个故障的不同方面,对于算法来讲都可以看成数据的维度。
研究的目标是将原始数据中最能表现故障特性的特征提取出来,为后面数据分类问题做好准备。
为了验证该方法在特征提取中的有效性,利用模拟传动轴实验台进行实验数据的采集。模拟传动轴实验台如图4所示。

图4 模拟传动轴实验台
在实验台上设置电机转速为480 r/s,频率为520 Hz,采集转动稳定后20 s的数据点,并在第10 s左右的时候,轻敲传动轴,传动轴受到突然冲击。模拟直升机受到突变载荷时传动系统受到的冲击,如武器袭击、风切变等。模拟传动系统突变冲击数据图如图5所示。
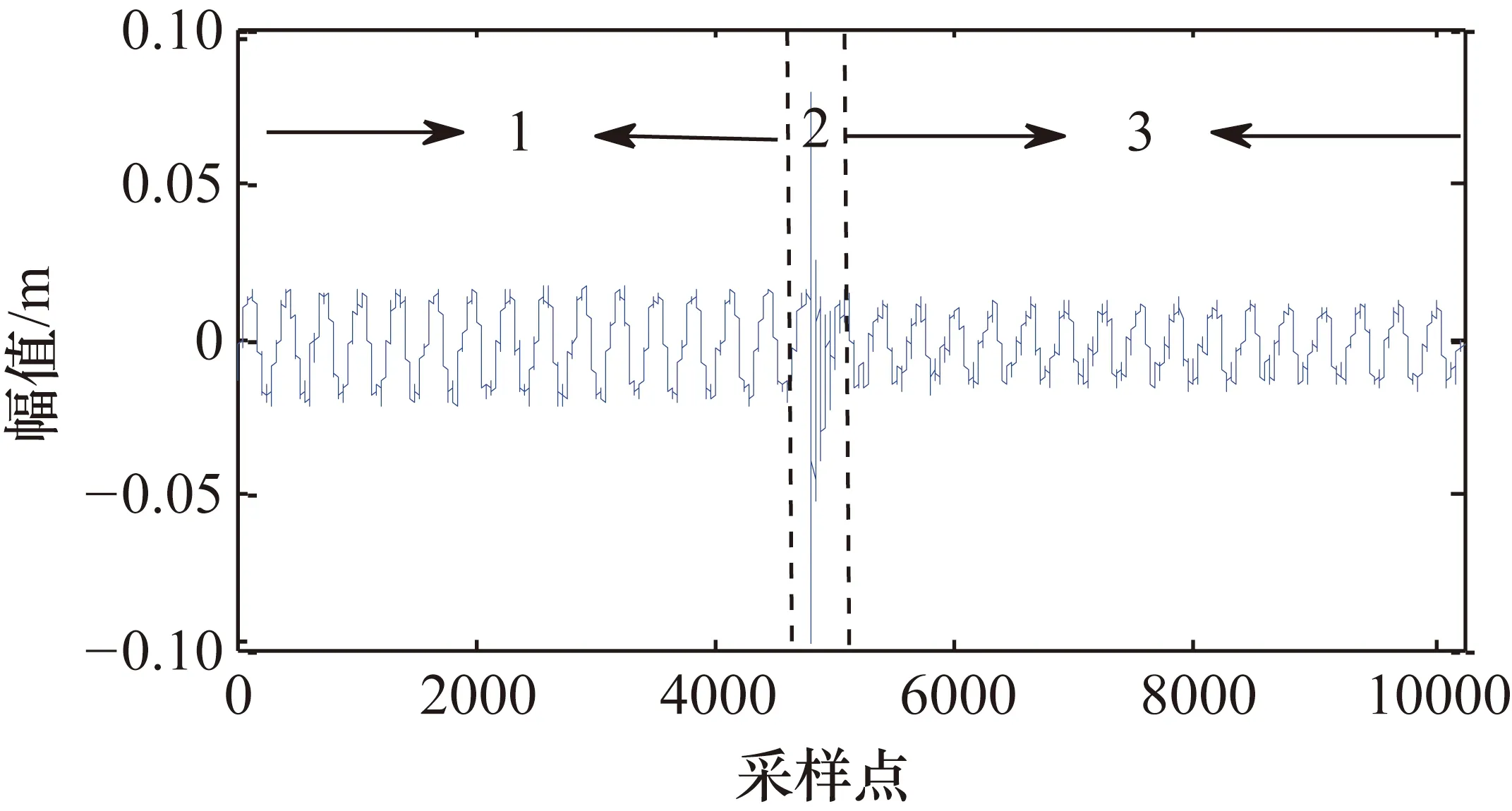
图5 模拟传动系统突变冲击数据图
可以明显看出数据在受到冲击载荷时被分成了3个部分。
将采集到的数据通过第3节介绍的步骤计算出故障特征,然后将数据分别导入近主成分分析法(PCA)、传统AP算法、改进后AP算法,得到的特征选择图如图6~图8所示。
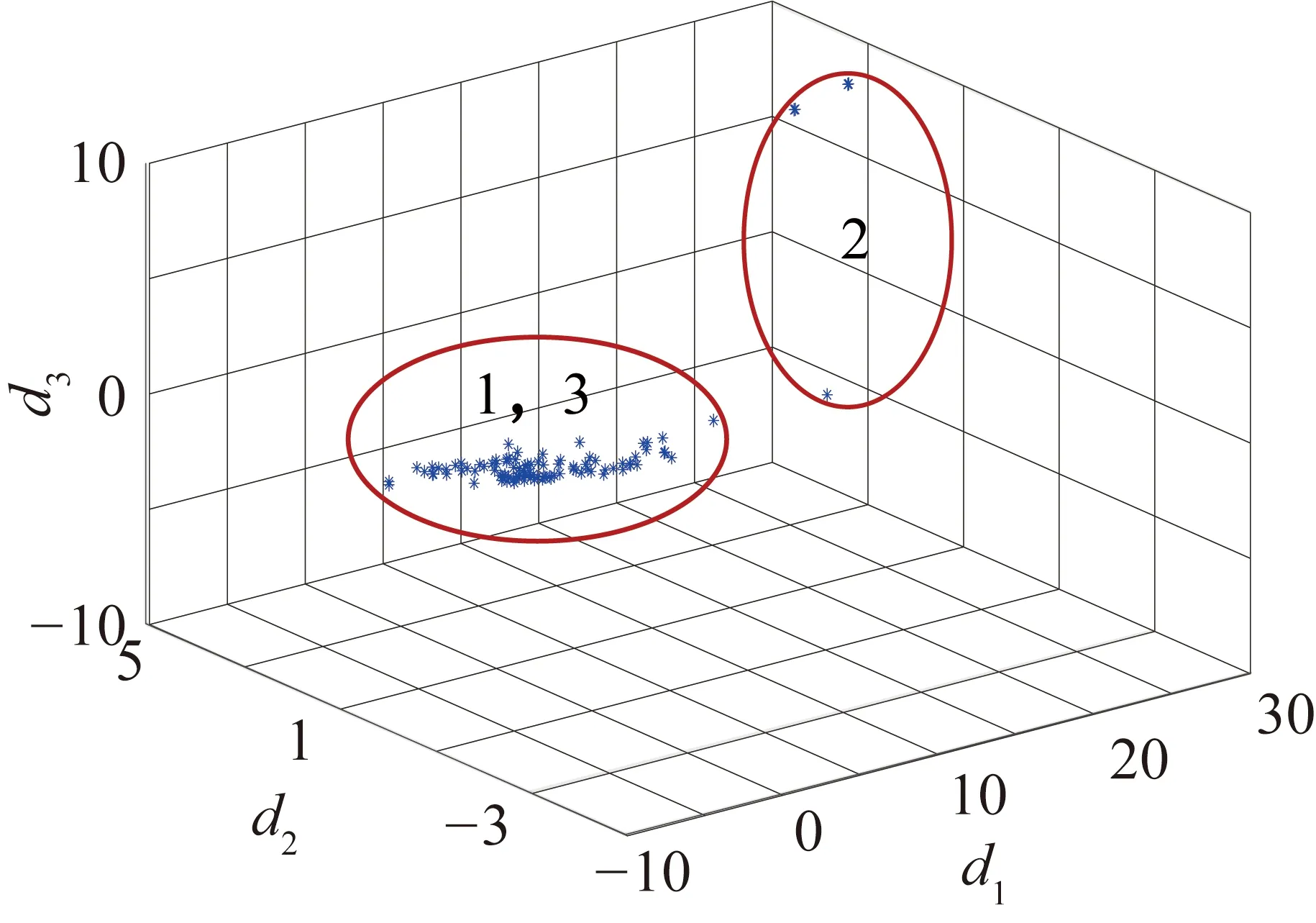
图6 实验数据PCA特征选择图
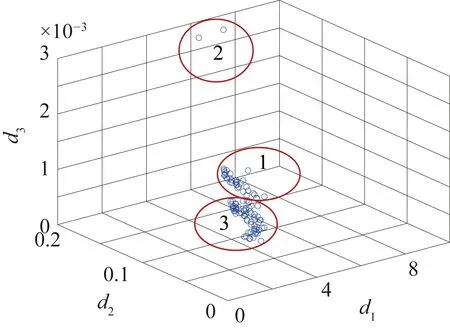
图7 传统AP聚类算法特征选择图
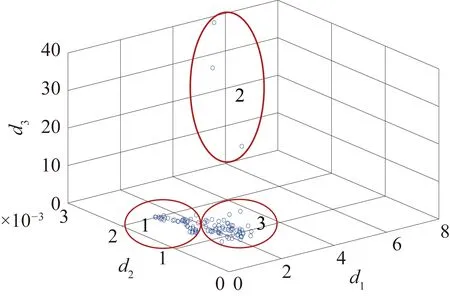
图8 改进AP聚类算法特征选择图
通过上面特征选择结果图来看,PCA选择的结果将数据分成了两类,将瞬间冲击数据(第2类数据)和冲击前数据(第1类数据)、冲击后数据(第3类数据)分开了,但是并未将数据1和数据3分开,不能把数据里的细小差异区分出来。传统的AP算法将数据分成了3个部分,这数据均被分离,效果也比较好,但是在对第1类数据和第3类数据进行细微差异的分辨时有部分数据分辨不清,第1类数据和第3类数据出现了重合,这对于故障诊断可能埋下诊断不清或者诊断不准确的隐患。而改进后的AP算法,将3类数据分离得很清楚,特别是对第1类数据和第3类数据有很好的分辨率,同时将第1类数据和第3类数据投影到同一面上,并将第2类数据也统一投影在一个面上,这说明对于一些相差比较大的数据改进后的AP算法也有较好的聚类效果。
5 结束语
本文提出了针对直升机传动系统故障特征提取的相似性传播聚类方法,对直升机传动轴进行了故障特征定义,理论推导和实验验证表明该方法对故障点特征具有良好的选择性。针对传统AP算法在分辨数据差异方面的不足,提出了一种度量特征重要度的加权AP算法,并将其应用于传动轴的故障特征选择上,实验结果表明,该算法分辨效果有了很大的提高,解决了传统AP算法对传动轴故障早期和细微故障的分辨率不高的问题。

