结合改进韦伯算子和加权稀疏表示的指静脉识别
李新春,张碧茜,林 森,马红艳
(1.辽宁工程技术大学 电子与信息工程学院,葫芦岛市 125105;2.辽宁工程技术大学 研究生院,葫芦岛市 125105)
0 引 言
手指静脉是一种皮下结构,随机生长成网状分布在手指上。静脉的生理特性使其高度安全,易于收集。此外,与其他的生物识别技术相比(即指纹[1]、人脸[2]、耳、虹膜[3]等),指静脉识别系统具备成像装置小、成本低、活动灵活、通用性强、可接受性高等特质。因此,手指活检在生物识别中具有很高的研究价值。
在指静脉识别的众多算法中,局部纹理特征提取方法不仅取得较好的识别效率,并且在光照及形变方面表现出良好的鲁棒性。在现有的研究中,杨文文等[4]采用简单二值化、局部二进制模式(local binary pattern,LBP)和分块主成分分析(principal component analysis,PCA)来进行指静脉识别,提高了识别精度,减少了处理时间。研究人员改进了传统的编码方法,提出了更多的特征描述。A.Prijono等[5]将LBP扩展到4个方向,提出了多方向局部线二进模式(multi-direction local line binary pattern,MDLLBP)方法。袭肖明等[6]提出了最佳局部差值编码(best local difference code bit,BLDCB)方式,并成功应用于手指静脉识别当中。近年来,研究人员又提出了关于特征局部结构图相关的一系列算法。TAO等[7]提出了正交对称局部图结构(orthogonal symmetric local graph structure,OSLGS),引入了高斯分布的差异来表示图像,而基于高斯分布的局部图结构存在着忽略图像方向信息的固有问题。董颂[8]提出多方向加权对称局部图结构(multi-orientation weighted-symmetric local graph structure, MOW-SLGS)算法。贾桂敏等[9]提出了对称邻域交叉图结构(symmetric cross-weighted local graph structure, SCW-LGS)的指静脉识别方法,相比于已有的算法,取得了较好的识别效果。由此,说明了将图论方法应用于指静脉识别具有十分重要的研究价值,但存在着对空间信息表达不完全使得特征提取不全面的问题。
通过上述分析,已有算法存在着对实验环境要求高,不能对噪声表现出很好的鲁棒性而导致识别率下降并且稳定性差的问题,本文考虑到拓扑结构相对简单的指静脉在识别过程中无法提取足够的有效特征并易受周围环境和噪声干扰问题,将传统的韦伯算子进行改进,提出一种韦伯局部圆梯度模式与多方位对称局部图结构结合加权稀疏表示分类的指静脉识别算法。首先利用Gabor细化了指静脉图像的纹理特征;然后对分解后的图像利用韦伯局部圆梯度模式与多方向对称局部图结构(Weber local circle gradient pattern-multidirectional symmetrica local graph structure,WLCGP-MSLGS)算法提取纹理特征;最后利用加权稀疏表示进行分类与匹配过程。在天津市智能信号与图像处理重点实验室数据库和马来西亚大学FV-USM (finger vein USM)图库上进行测试实验,结果表明,与其他传统及最新算法相比,本文算法提高了系统的识别率,具有一定的优势。
1 相关理论
1.1 韦伯局部描述
文献[10]首先受到韦伯定律的启发提出了韦伯局部描述符(Weber local descriptor,WLD)。该定律指出,只有当刺激变量与刺激本身的比值达到一定阈值时,才能看出两者的区别,表示为
(1)
(1)式中:I为初始刺激强度;ΔI为增量阈值;K表示为比例的不变常数。
局部窗口如图1,WLD算子利用3×3滤波器来计算当前像素的灰度变化。实践证明,该方法不仅有效,而且效果显著。

图1 局部窗口Fig.1 Local window
WLD由差分激励和算子方向2部分组成。差分激励描述中心像素与相邻像素之间的强度变化表示为
(2)
(2)式中:P表示中心位置相邻像素的个数;gi(i=0,1,…,P-1)表示相邻像素的灰度值;gc为中心像素(xc,yc)的灰度值。当输入像素值过大或过小时,反正切函数能够使输出量在合理范围内。
WLD的方向部分表示图像中像素的梯度变化,可以表示为水平方向变化量与垂直方向变化量之比,表示为
(3)
将差分激励与方向信息2个分量相结合,构造出表示WLD特征的二维级联直方图。
1.2 LGS和SLGS
局部图结构(local graph structure,LGS)利用图论来描述相邻像素的灰度差,并将其编码为二值模式。它构造一个图来探究目标像素与周围5个像素之间的关系。LGS的计算过程:在目标像素的左侧,从目标像素开始沿逆时针方向进行对比,若箭头指向的顶点像素灰度值大于箭尾指向的像素值,则在连接这2个顶点的边缘上赋值1,否则赋值为0;相反地,该过程在目标像素的右侧进行,但像素值按顺时针方向进行比较;最后,将8位二进制数转换为十进制数,以获得目标像素的LGS值。图2描述了LGS的编码过程,其中目标像素的灰度值为27。
LGS(10101001)=1×27+0×26+1×25+0×24+
1×23+0×22+0×21+1×20=
169
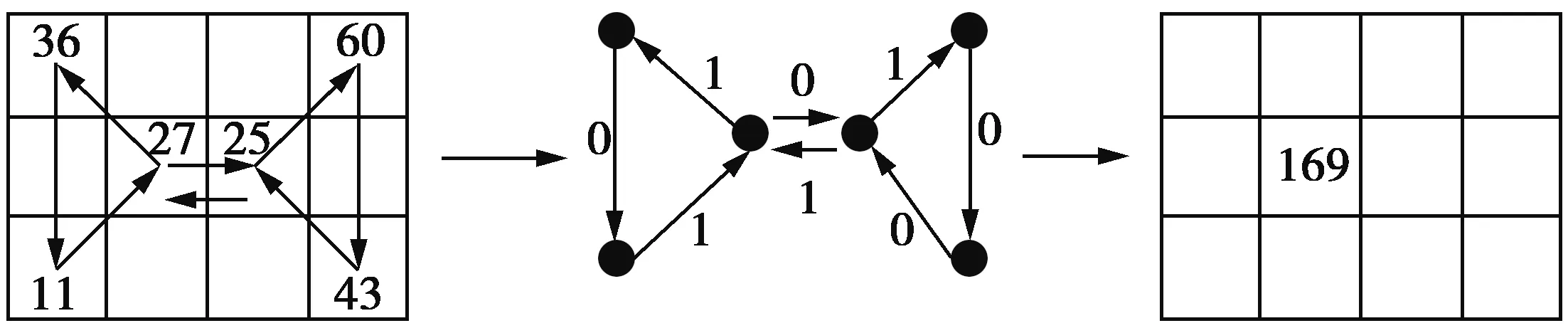
图2 局部图结构LGS算子Fig.2 Localgraph structure LGS operator
与LGS相比,对称局部图结构(symmetrical local graph structure,SLGS)采用对称结构来保持权重的平衡,目标像素的左右各包含3个像素。SLGS算子如图3,SLGS算子只描述了水平方向的梯度信息,缺乏对空间结构的表达性。
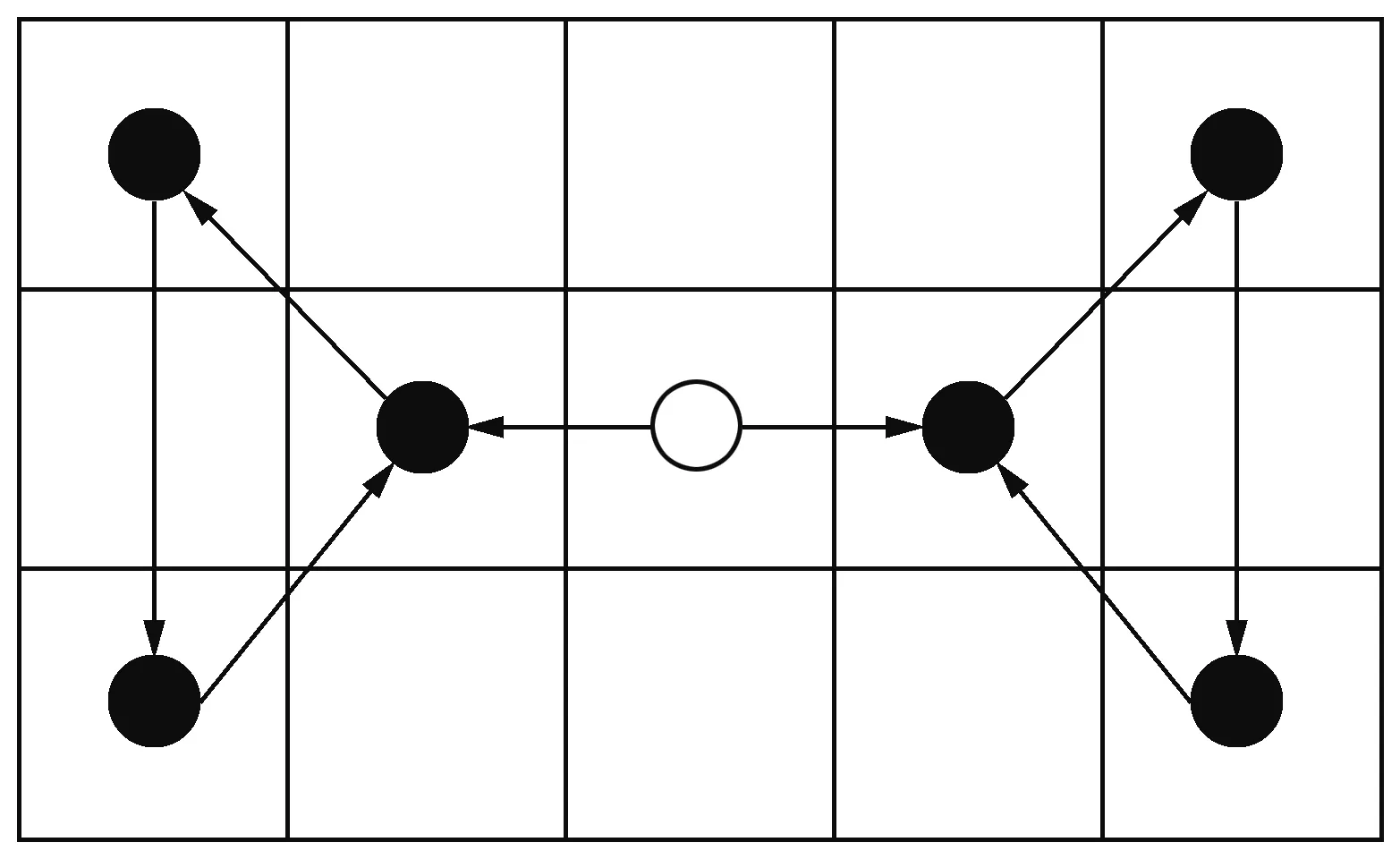
图3 局部图结构SLGS算子Fig.3 Localgraph structure SLGS operator
2 特征提取算法
基于该算法的系统框架如图4。其主要步骤包括:Gabor特征提取、一种新的WLD算子和基于加权稀疏表示的分类(WLD-sparse representation based classification,WSRC)。

图4 整体识别过程Fig.4 Entire identification process
2.1 Gabor特征
Gabor小波滤波器是一种线性滤波器,已成功地应用于手指静脉识别中。Gabor核类似于简单神经元细胞的二维接受域,可以描述指静脉图像的空间信息和频率特性。因此,Gabor特征增强了指静脉图像关键区域的局部纹理细节,对光照变化具有鲁棒性。简化后的Gabor滤波器[11]表示为
(4)
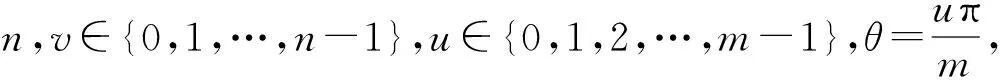
为了提取Gabor信号的有效幅度,降低Gabor特征向量的维度,在n尺度和m方向上融合Gabor特征,表示为
(5)
(5)式中:Gu,v(x,y)表示每个尺度对应m个方向的Gabor特征图像;MGv(x,y)为v尺度融合像素值的平均值。
2.2 改进的韦伯算子
虽然WLD和LGS具有良好的识别性能,但它们仍然存在一些缺点。WLD描述符忽略了中心像素的相邻的径向像素灰度值之间的关系,LGS的新颖之处在于引入了相邻像素之间的像素强度变化,但在目标像素的左侧分配了较大的权重,导致最终的LGS值由部分邻域决定,从而LGS对局部纹理变化很敏感。为了解决上述问题,本文提出了WLCGP-MSLGS。
2.2.1 改进差分激励
为避免WLD算子只考虑中心像素与径向周围像素间的灰度关系,忽略了周围像素更有鉴别性和有效性的信息,本节提出一种新的局部描述符,称为WLCGP,它对图像的变化可以更加稳定地表达。WLCGP的图解如图5。
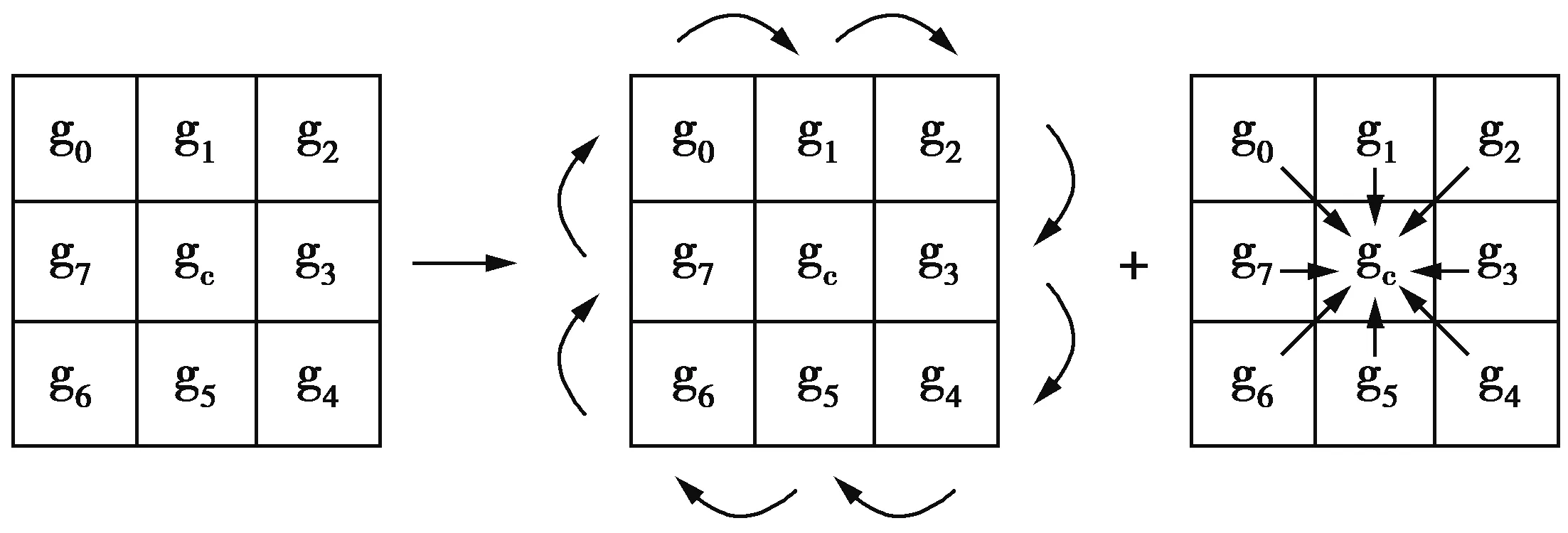
图5 WLCGP图解Fig.5 WLCGP diagram
其数学定义为
(6)
sum1=|g0-g1|+|g1-g2|+|g2-g3|+
|g3-g4||g4-g5|+|g5-g6|+
|g6-g7|+|g7-g0|
(7)
(8)
(9)
(6)—(9)式中:gm为8个相邻像素和中心像素的平均值,sum1为顺时针方向上所有外围相邻像素间梯度关系之和;sum2为目标像素与周围8个像素间梯度关系之和。
图5中,使用3×3邻域模板,利用(7)式计算8个周边像素沿顺时针方向的梯度关系,利用(8)式描述目标像素与周围其他像素的梯度关系。为了更加稳定,该算子用(8)式中gm表示计算包括3×3邻域模板和中心像素在内的9个像素的平均强度;最后,再利用反正切函数,通过计算图像的周期梯度信息和整体梯度信息,提高WLCGP对噪声的鲁棒性。
2.2.2 改进LGS
为解决传统LGS算法方向单一,表达局部纹理信息不全面的问题,本节提出了一个新的描述符MSLGS,多方位对称局部图结构如图6。图6中,MSLGS分别在0°,45°,90°,135°方向上通过5×5过滤器窗口计算特征值。
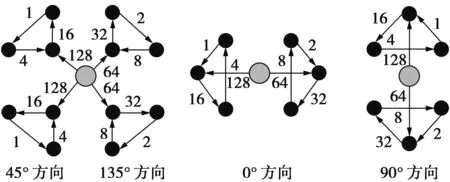
图6 多方位对称局部图结构Fig.6 Multi-orientation symmetrical local graph structure
图7—图10分别给出了MSLGS在0°,45°,90°,135°方向的例子。图8说明了在计算MSLGS的45°方向过程中,目标像素被描述为灰色的颜色,并且135°方向上的特征值的计算方法与45°方向上的特征值的计算方法相同,即目标像素左上方的比较按逆时针方向进行,目标像素右下方的比较按顺时针方向进行。MSLGS结构在0°,90°方向的编码方式不同于其他算法,非常接近目标像素的4个像素赋予了更多的权重,由此更好地强调了对目标像素的影响。
0°MSLGS(10001100)=1×27+0×26+0×25+0×24+
1×23+1×22+0×21+0×20=
140
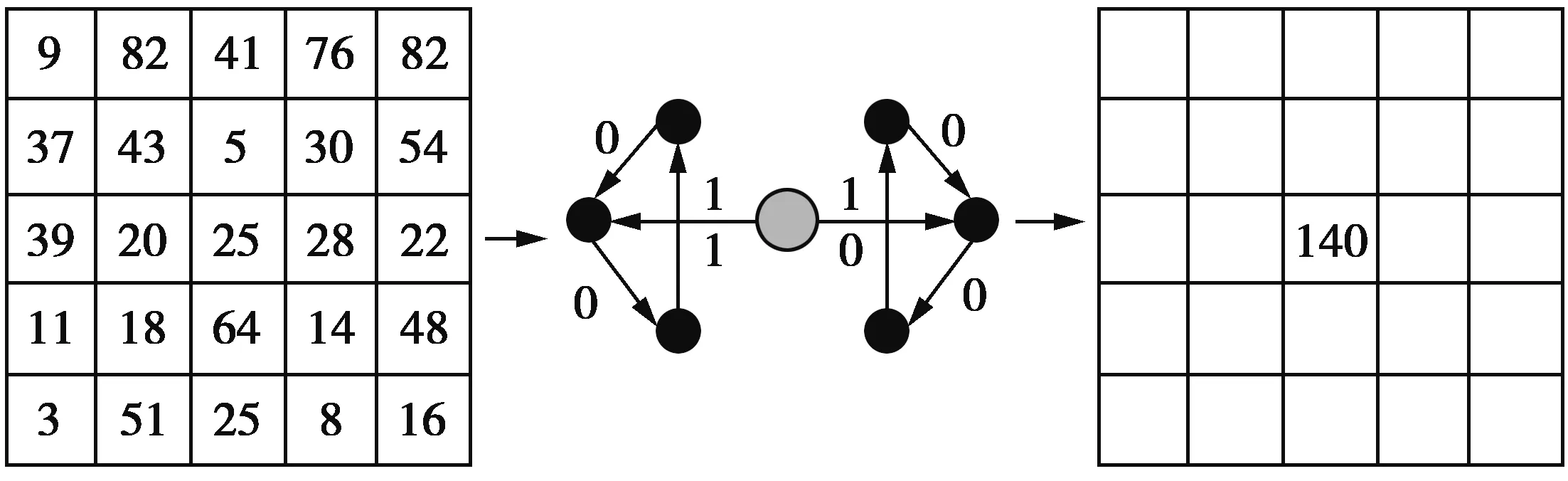
图7 MSLGS在0°方向的例子Fig.7 Demonstration of MSLGS operator in 0°direction
45°MSLGS(01100001)=0×27+1×26+1×25+
0×24+0×23+0×22+
0×21+1×20=97

图8 MSLGS在45°方向的例子Fig.8 Demonstration of MSLGS operator in 45°direction
最后,MSLGS算法可以得到4个特征值。4个特征值可以反映中心像素与邻域像素点之间的位置信息和梯度信息,并且不管图像怎样旋转,分别提取多个方向的特征编码,总会得到一个最大值,若一个方向的特征值越大,则表明像素灰度值的差异越大。因此,本文选择最大的特征值替换该位置原本的像素值,因为它反映了图像细节最具代表性的特征,并可以解决旋转不变性问题。
90°MSLGS(10010011)=1×27+0×26+0×25+
1×24+0×23+0×22+1×21+
1×20=147
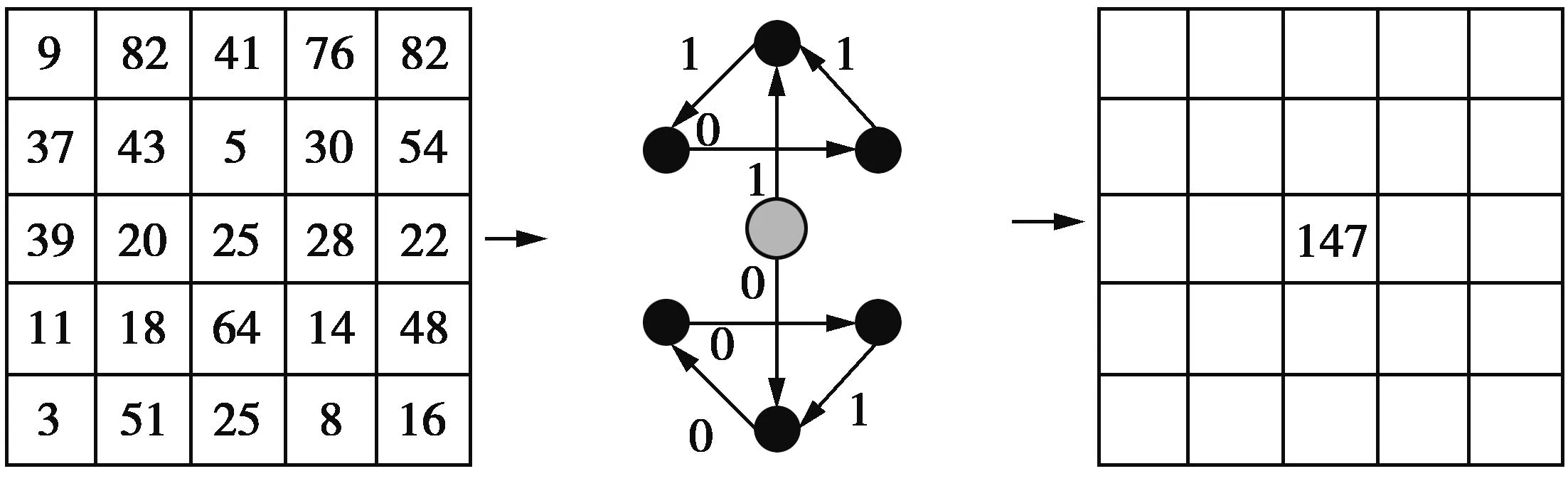
图9 MSLGS在90°方向的例子Fig.9 Demonstration of MSLGS operator in 90°direction
135°MSLGS(10111100)=1×27+0×26+1×25+1×24+
1×23+1×22+0×21+
0×20=188
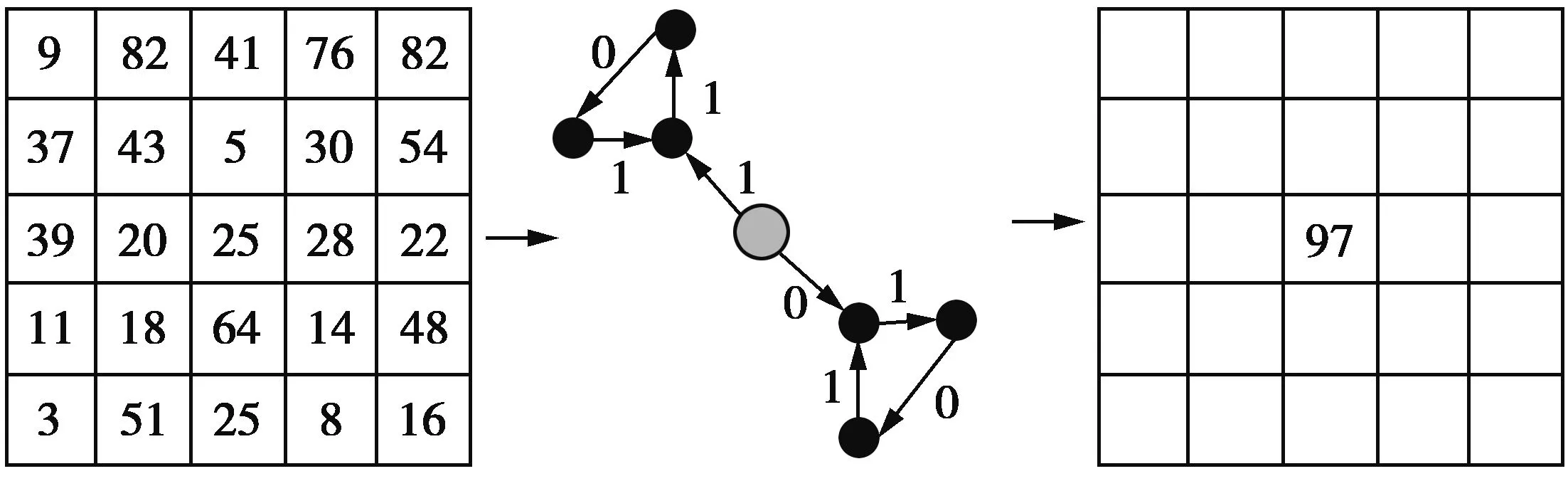
图10 MSLGS在135°方向的例子Fig.10 Demonstration of MSLGS operator in 135°direction
2.3 WLCGP-MSLGS直方图
对于给定的一张指静脉图像,首先计算出WLCGP和MSLGS特征向量,然后将其组合为二维WLCGP-MSLGS直方图,出于增加特征区分性及加强特征描述能力的目的,本文对二维直方图按列优先连接成一个一维直方图,用来表示指静脉图像的纹理特征。
3 由粗到细的指静脉识别方法
结合WLCGP-MSLGS和WSRC,本节提出了一种指静脉识别方法,它包括2个阶段,即粗识别阶段和精识别阶段。在粗识别阶段,识别并保留与测试样本非常相似的少数类别,并舍弃其他大部分类别的冗余训练样本;在精识别阶段,提取WLCG-MSLGS直方图矢量,并通过WSRC算法识别测试样本。假设n个来自N个不同的类{X1,X2,…,XN}中有原始指静脉x1,x2,…,xn作为训练集,ni是第i类的指静脉编号,y是测试样本。
3.1 粗识别阶段
同一类图像的旋转、位置和分辨率之间的差异很小,而不同类之间的图像差异很大。假设有n个指静脉属于N个不同的类别和一个测试指静脉y,xij是第i个类别的第j个指静脉。任何2个指静脉xi和xj之间的相似性被定义为
(10)
(10)式中,‖xi-xj‖为xi和xj之间的欧式距离。
那么2个指静脉之间的不相似性被定义为
w(xi,xj)=1-‖xi-xj‖
(11)
根据(10)式计算测试样本与每个类别中的一个手指静脉之间的相似度,并将它们排序为s(y,xr11)≥s(y,xr21)≥…≥s(y,xrM1)≥…,然后取前M个最大相似度的M个类{xr1,xr2,…,xrM}作为测试样本的候选类,并保留这测M个候选类别的训练样本,并且来自其他N-M个类的所有训练样本从训练集合中被舍弃。
3.2 精识别阶段
结合WSRC,在本小节中提出了指静脉识别方案。在上述粗略识别阶段,M个候选类别{xr1,xr2,…,xrM}被保留。从M个候选类别和测试样本的每个训练样本中提取WLCGP-MSLGS直方图向量,记为{Hr1,Hr2,…,HrM}和hy,其中,Hij是第i类的第j个WLCGP-MSLGS直方图矢量。在WSRC中,{Hr1,Hr2,…,HrM}被用作为新的训练集来将测试样本和每个训练样本之间的相异性信息输入到SRC中的权重构造中,提出了一种WSRC算法用于指静脉识别。该算法解决了以下加权l1范数最小化问题。
(12)
(12)式中,W′是一个对角矩阵,diag(W′)=[w(y,xr11),w(y,xr12),…,w(y,xrmnrm)]T,其中,xrij是第ri类上第j个原始指静脉图像,y是原始测试图像,nrm是第ri类中的指静脉编号。(12)式可以使用标准线性规划方法来解决。在加权矩阵中,较大的w(y,xrij)表示y和xrij之间的不相似度。因此,WSRC可以生成更多的判别稀疏代码,从而更鲁棒地表示测试样本。在线性表示中,WSRC的稀疏系数趋于局部。得到稀疏系数后,将查询图像识别为重构误差最小的类,残差计算为
(13)
(13)式中,Ari为对应于第ri类的稀疏系数向量。
判断测试样本y类别为
Identity(y)=argmini{ei},
i=1,2,…,M
(14)
3.3 识别算法总结
识别算法流程如图11,该算法的主要步骤如下。
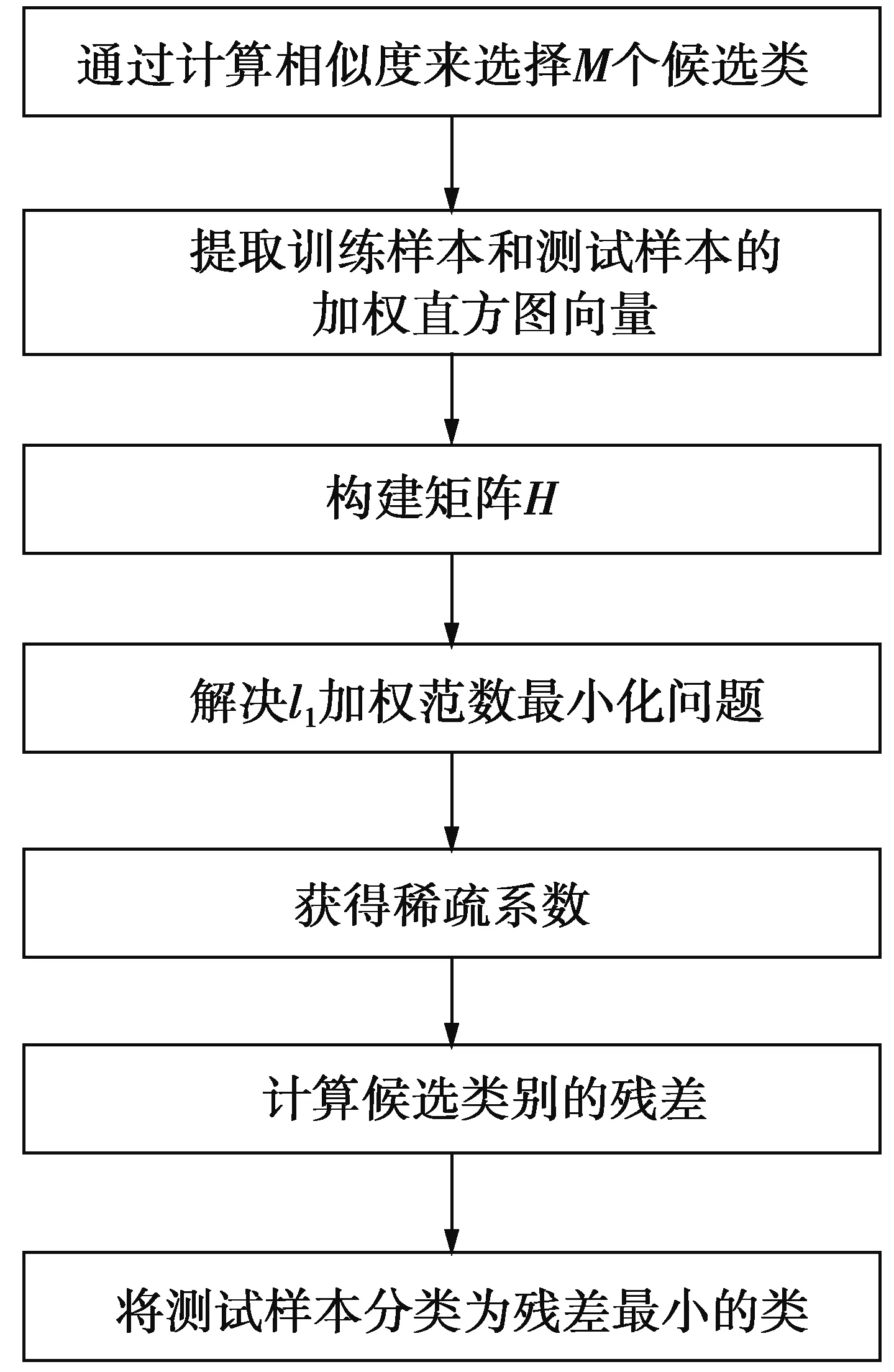
图11 识别算法流程Fig.11 Flowt of recognition algorithm
输入:来自N个不同类的n个训练图像、测试的指静脉图像y、候选类M、在WSRC中的参数λ。
步骤1计算测试样本与每个训练类的第1个指静脉之间的相似性,然后保留前M个最大相似性的M个候选类作为训练样本;
步骤2用WLCGP-MSLGS算法提取每个候选训练样本和测试样本的加权直方图向量;
步骤3用候选训练样本的所有加权直方图向量构造字典矩阵H;
步骤4利用(10)式计算y与各候选训练样本之间的相似度,利用(11)式计算不同度,利用不同度构造权重矩阵W;
步骤5构造并求解加权l1范数最小化问题;
步骤6得到稀疏系数;
步骤7通过(13)式计算M个候选类的残差;
步骤8根据(14)式将y分类为残差最小的类。
输出:对测试样本集中的每个测试样本重复步骤1—8,并计算每个类别的识别精度。
4 实验图库和评价指标
实验环境为Windows 7系统中2015a版本的Matlab软件,处理器是Intel(R) Core(TM) i3-2 120 CPU,主频是2.30 GHz,内存(RAM)是4.00 GByte。
4.1 实验图库
1)实验图库1。本实验采用天津市智能信号与图像处理重点实验室数据库[12],作为实验图库1。该数据库中有64个手指样本,每个样本有15幅分样本。该实验中的指静脉图像噪声小,指静脉路清晰可见。
2)实验图库2。本实验采用FV-USM数据库[13],作为实验图库2。该数据库中的图像源于123名取样者,提取每位的除了大拇指的4个手指的分样本,共492个手指类和2 952张(123×4×6)图片。
4.2 评价指标
为了验证本文所提算法的性能,本文评价指标为正确识别率[14](orrect recognition rate,CRR)。CRR表示为识别系统可以正确区分的次数与实验总次数的比值,计算式为
(15)
(15)式中:VC表示识别结果为正确的次数;VS表示实验总的次数。
5 数据仿真及分析
5.1 Gabor尺度和方向参数选择
参数的选取会直接影响系统的识别性能。因此,本文通过在图库1和图库2上的实验来选取Gabor尺度和方向的最优参数。利用(10)式获取指静脉识别率。
分析表1可知,虽然Gabor方向参数为4时的识别时间比Gabor方向参数为8和16时的识别时间稍短,但其识别率明显低于Gabor方向参数为8和16时的识别率。Gabor方向参数为16和8时相比,在尺度参数相同情况下,识别率增加极小,但识别时间却大幅度增大。因此,Gabor方向参数为8时,可以满足识别的准确性,且可满足实时性。尺度参数为5~7时的识别率增长幅度小于尺度参数为3~5时的识别率增长幅度,但是尺度参数为5~7时的识别时间增长幅度大于尺度参数为3~5时的识别时间增长幅度。因此,通过综合考虑识别时间和识别精度,本文选取5个尺度8个方向的Gabor细化纹理特征。
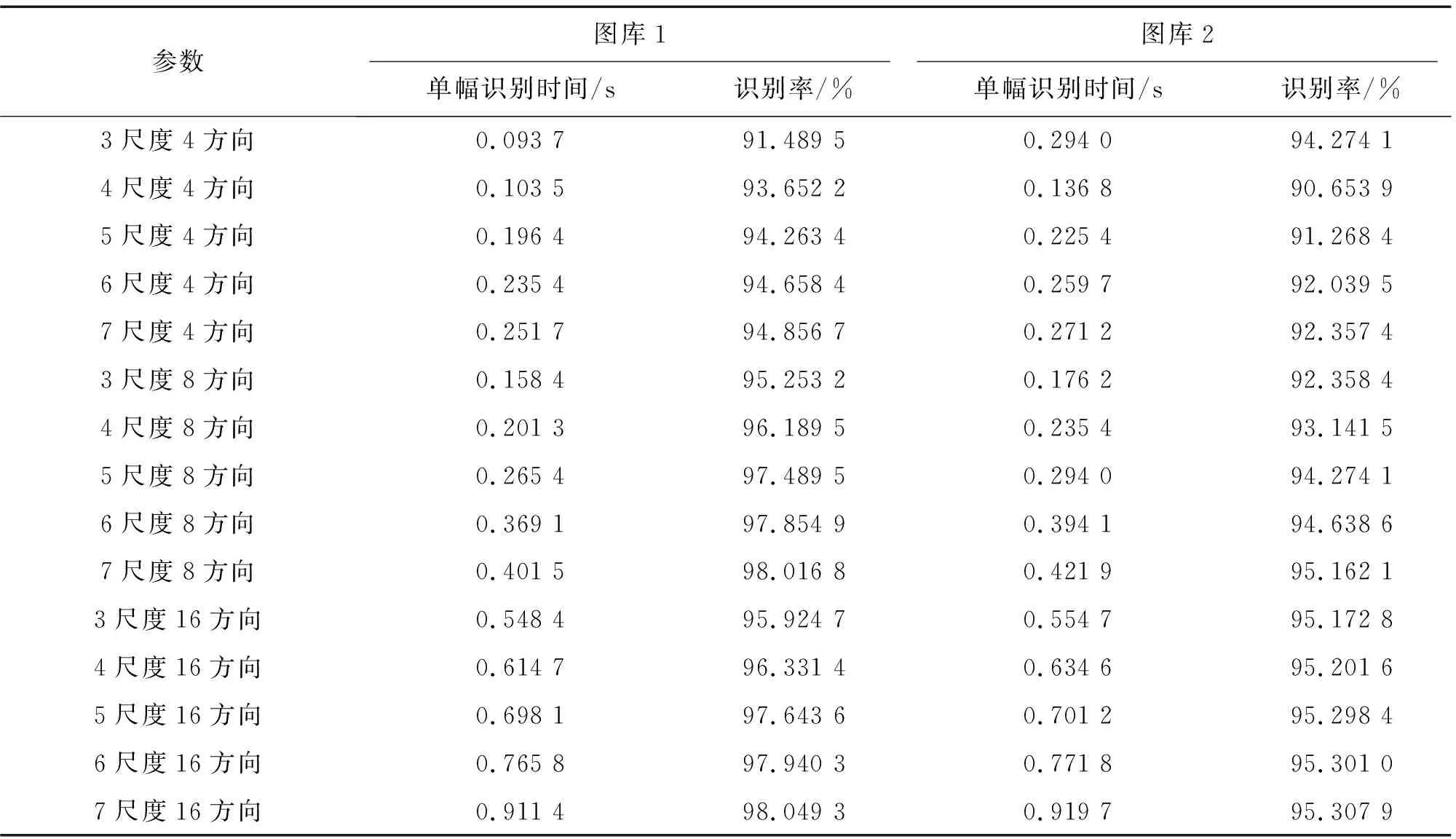
表1 2个图库中在Gabor不同尺度参数和不同方向参数下的识别率和识别时间

图12 指静脉图像对应的40张Gabor特征图Fig.12 40 Gabor feature images corresponding to image of finger vein
5.2 图库1上的实验
1)实验1。选取每类的前8个指静脉图像作为测试样本集[15],后7个指静脉图像选为测试样本集。为了清楚地观察到相似度的变化,图13展示了第1类的第9张指静脉图像作为测试样本分别与每个类的第1张指静脉图像之间的相似性。
从图13中可看出,有25个相似度大于0.2,有13个相似度大于0.3,而测试样本与第1类指静脉图像的相似度高达0.89,这也表明了同一类中的不同样本的相似度远远高于2个来自不同类别的指静脉之间的相似度,则相似度可以用来分类指静脉图像。图13中表明,超过三分之二的相似性小于0.2,因此,本文实验中仅保留总类数的三分之一作为粗识别阶段训练候选类。

图13 图库1上测试样本与每类第1张图的相似度Fig.13 Similarity between the test sample and the first graph of each class in gallery 1
2)实验2。为验证本文算法对噪声及环境的鲁棒性,随机在每个候选类中添加一个干扰指静脉图像。干扰指静脉图像包括高斯噪声、盐椒噪声、斑点噪声、错位和损坏样本。图14显示了每个干扰指静脉图像与图库中第1类第1个指静脉图像的相似性。从图14中可以看出,最后4个相似度非常小,表明测试样本与异常图像非常不相似。因此,在WSRC中,这些样本将被赋予更大的权重。
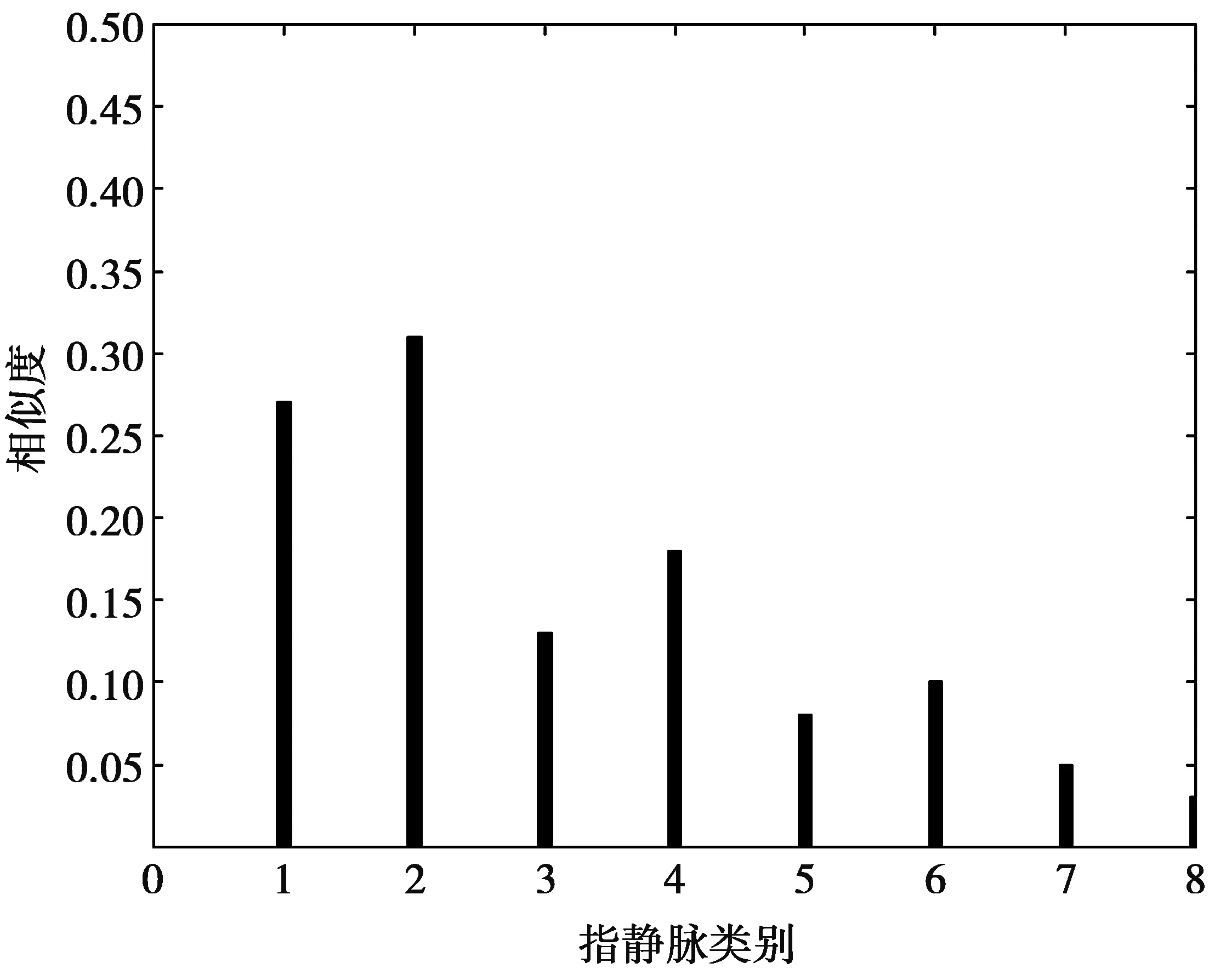
图14 干扰图与第1类第1张图的相似度Fig.14 Similarity between the interference pattern and the first graph of the first class
5.3 图库2上的实验
利用上述方法在实验数据库2上进行了实验。选取每类的前3个指静脉图像作为测试样本集,后3个指静脉图像选为测试样本集。同样选取相似性高的前三分之一类作为保留训练候选类。在实验2中,同样在每个候选类中混入一个干扰指静脉图像。图库2测试样本与每类第1张图的相似度如图15。
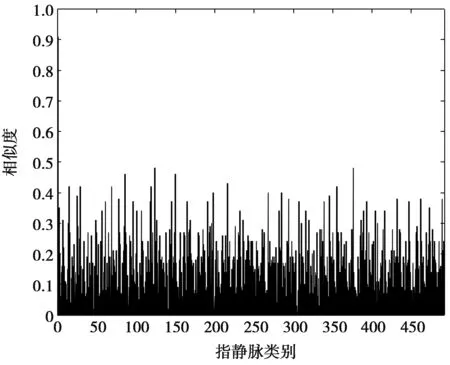
图15 图库2测试样本与每类第1张图的相似度Fig.15 Similarity between the test sample and the first graph of each class in gallery 2
为了更清晰地观察到相似度的变化,图16仅显示了前50类中第1张指静脉图像与测试样本的相似度。从图15中可看出,有21个相似性大于0.2,只有10个相似性大于0.3,而测试样本与第1类指静脉图像的相似度高达0.91,本实验中仍有超过三分之二的相似性小于0.2,那么仍然仅保留总类数的三分之一作为粗识别阶段训练候选类。
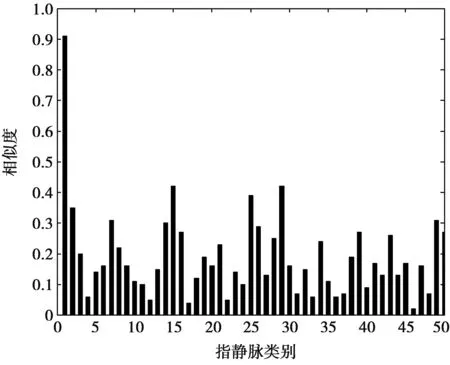
图16 图库2测试样本与前50类第1张图的相似度Fig.16 Similarity between the test sample and the first graph of the top 50 categories in gallery 2
5.4 实验结果及分析
5.4.1 算法有效性实验结果及分析
为进一步验证本文算法的有效性,将本文算法与传统的LBP,LLBP,LDP和改进前的算法WLD,WLCGP,SLGS,MSLGS和WLCGP-SLGS及最新提出的基于Gabor和Curvelet的近邻二值模式手指静脉识别方法[16],SCW-LGS算法和DBD[17]算法进行比较,结果如表2和表3。分析表中数据可知,在相同条件下,本文算法在实验1的单幅图像识别时间分别为0.018 8 s和0.025 1 s,在实验2的单幅图像识别时间分别为0.017 1 s和0.023 7 s,均小于其他算法所用时间。这种时间优势主要由于本文在粗识别阶段基于相似度简单而快速地排除了大部分指静脉类,从而大大降低了计算成本。WLCGP-MSLGS算法的鲁棒性及WSRC在数据线性和局域性方面的优点使得本文算法提取指静脉图像特征获得的CRR值大于传统算法及最新算法,由表3可看出,即使混入干扰的训练集样本也可得到较好的识别效果。有效表明本文算法更好地获取了指静脉图像纹理特征信息,使得系统识别性能更好,能够实现高效可靠的身份识别。
5.4.2 算法鲁棒性实验结果及分析
为验证本文算法对噪声的鲁棒性,将图像加入2种具有代表性的典型噪声,即噪声密度为0.05的椒盐噪声和均值为0、方差为0.01的高斯白噪声,结果如表4。分析表4中数据可知,在加入椒盐噪声和高斯白噪声的条件下,本文算法的识别率仍均大于其余算法,受噪声影响小,表现出对噪声较强的鲁棒性。这种鲁棒优势主要由于该算法首先利用Gabor小波变换的频率及方向选择性,提取出指静脉图像的多尺度多方向上的Gabor特征,多尺度多方向性可有效弱化噪声。提出的WLCGP不仅考虑了中心像素与径向周围像素间的灰度关系,并且考虑了径向周围像素之间的灰度关系,可得到更有鉴别性的受噪声影响小的信息,使本文算法的鲁棒性提高,具有可行性。

表2 2个图库中不同算法实验1的识别率和识别时间
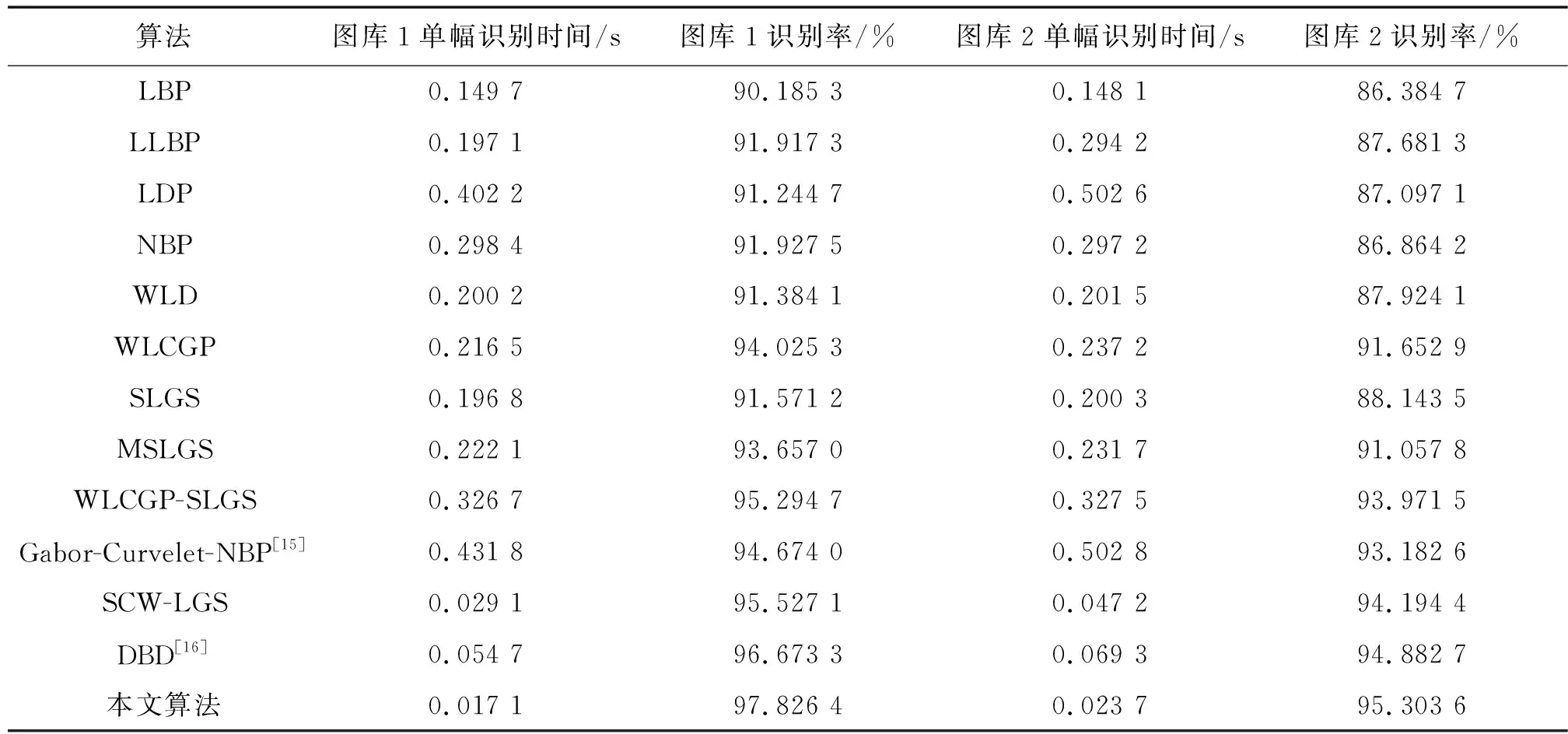
表3 2个图库中不同算法实验2的识别率和识别时间
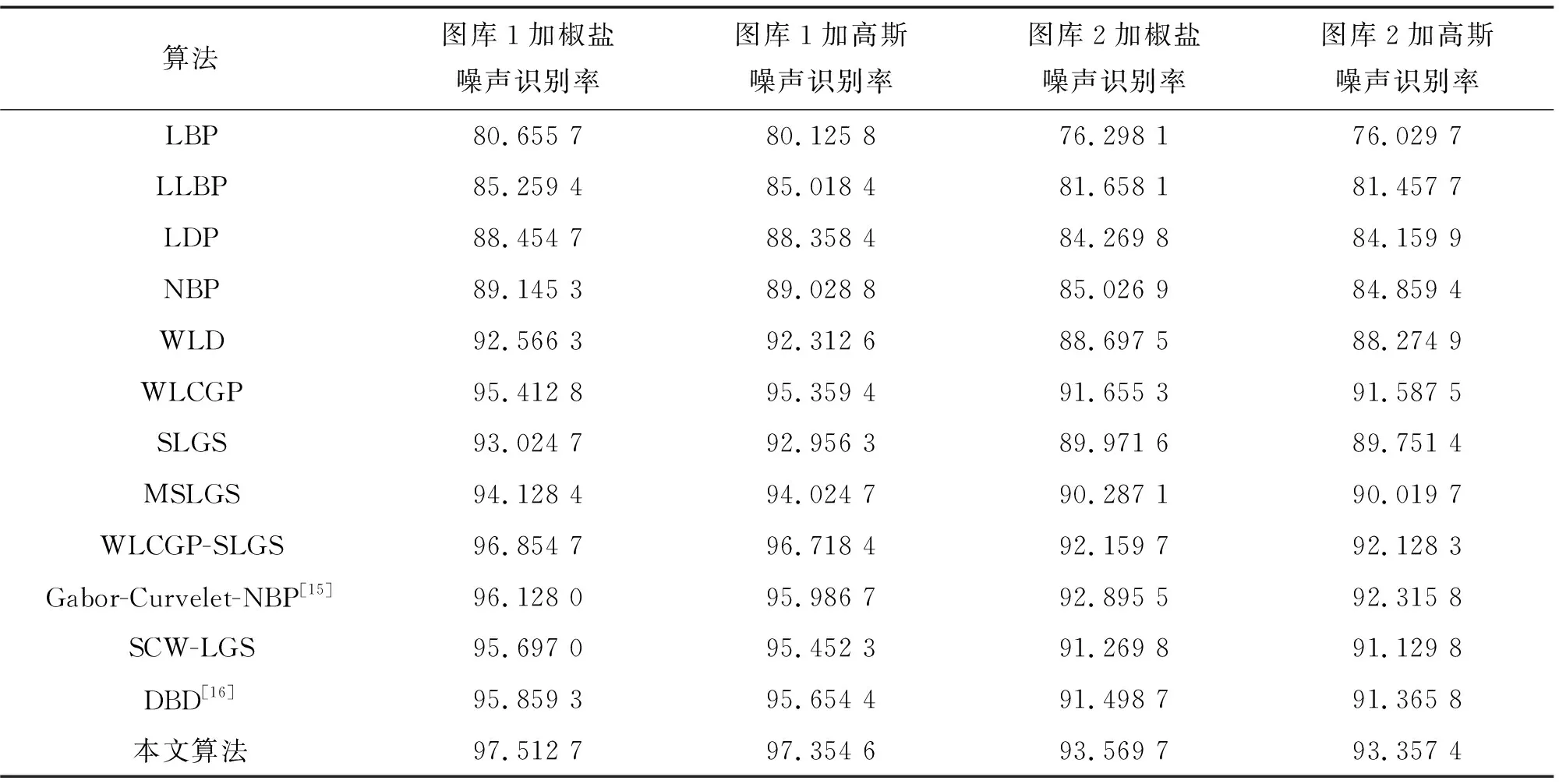
表4 2个图库中加入噪声后不同算法的识别率
4 结束语
为了在拓扑结构简单的指静脉图像上提取更完整的纹理信息并提高识别效率,本文提出了一种基于WLCGP-MSLGS结合WSRC的由粗到细指静脉识别算法。在粗识别阶段,确定测试样本的少数候选类别;在精识别阶段,确定测试样本的最终类别。该方法的主要原理是合理地将分类问题简化为类数较少的简单分类问题。在特征提取阶段,提出了WLCGP-MSLGS算法,能有效提取细化纹理。在匹配识别阶段,用加权稀疏来表示分类完成最终的识别匹配。在2个实验图库上进行对比实验,单幅图像识别时间分别为0.018 8 s和0.025 1 s,识别率分别为99.354 6%和97.384 2%。结果表明,该方法具有一定的优势,既满足了识别的实时性,又可获得较好的识别效果,具有实际应用前景。

