煤炭全自动制样系统精密度检验方法研究

何文莉，张太平，朱琦妮,白志军

(1.江西光明智能科技有限公司，江西 南昌 330096；2.国网湖北省电力有限公司电力科学研究院，湖北 武汉 430077;3.河北建设投资集团有限公司，河北 石家庄 050051)

0 引 言

煤炭全自动机械制样系统的精密度(以方差表示)估计并判定其是否符合预期目标值，此为1项重要的质量保证工作，对于交货验收、运行使用意义重大。

针对煤炭全过程的制样程序，美国标准ASTM D 2013-07[1]附录A2和国际标准ISO及其最新版本ISO 13909-7:2016 (E)[2]第9章分别给出了制样和化验总方差的测试与评定方法。与ISO标准相对应，国家标准GB/T 19494.3[3]第4.5章也有相同的内容。

国内无论人工制样程序还是半自动的破碎缩分联合制样以及全自动制样系统精密度试验均基本采用国家标准。但实际上机械制样包括全自动制样系统工作程序与ASTM、ISO和国标中列举的两阶段制样程序不同，精密度检验方法不能完全照搬国内外标准。此外ISO和国标中有关精密度检验判断方法的表述稍显简捷，有些内容还存在不同的理解。

以下针对煤炭全自动机械制样系统的精密度检验中存在的3个重要问题进行深入讨论：① 精密度的概念和点估计方法；② 制样和化验总方差目标值(期望值)确定；③ 制样精密度的合格判定等。

1 煤炭全自动制样系统组成和制样流程

煤炭全自动制样系统是将称重设备、破碎设备、缩分设备、干燥设备、除铁设备、除尘设备、试样分装标识设备、输送(搬运)设备等按规定工序和流程有机组合并在无人工辅助下通过控制系统自动完成一般分析试验煤样、存查煤样、全水分试样等的全部制备操作包括进样、称重、输送、除铁、破碎、缩分、干燥、粉碎、除尘以及留样转运、试样收集封装标识、废样回收等的1种高度自动化的机械系统。根据制样过程中样品转移方式究竟是斗提+胶带机还是工业机器人，自动制样系统可分为生产流水线型、工业机器人型。也有相关研究对该2种典型自动制样系统的结构、工艺流程和主要性能试验结果等进行了深度探讨[4-12]。

从本质上分析，全自动制样系统的整个制样过程实质上为三阶段的制样流程或四阶段制样和化验流程，如图1所示。

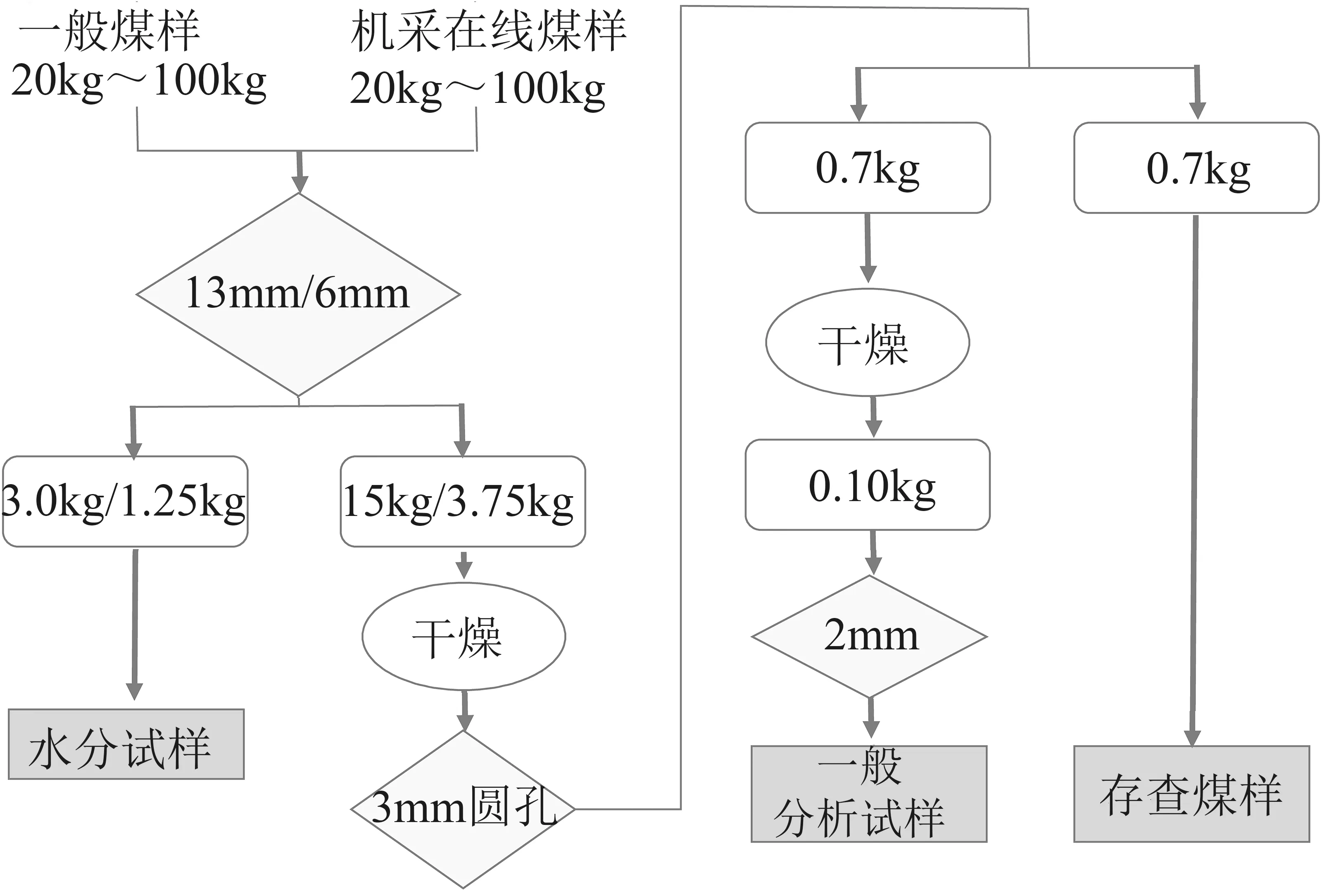
图1 全自动制样系统制样流程

2 全自动制样系统精密度的估计

2.1 制样精密度的概念与点估计方法

国内外标准均未给出制样精密度的定义。通常，精密度是指规定条件下独立测定结果之间的符合程度，取决于随机误差的概率分布，一般用总体标准偏差来度量。制样精密度可定义为规定的制样条件下所制备的独立试样测定结果间的符合程度，考虑到制样各阶段和化验过程之间随机误差的联系，用试样灰分或水分的总体方差(标准偏差的平方)来度量。“规定的制样条件”应指对于同一品种、同一批次大体相同特性的煤炭按同样的制样程序、在同一制样系统使用完全相同的运行参数进行制样的条件。“独立试样”指规定条件下所获得试样不相关且不受以前任一试样的影响。

但某一特定制样程序的精密度并非已知，需通过专门的试验来估计。结合统计学原理[13-16]，精密度(标准偏差)点估计通常有单样本重复试验法和多样本等精度联合试验法。

2.1.1 单样本重复试验法

对同一对象在相同条件下测定n次，由公式(1)计算样本标准差作为总体标准差σ(精密度)估计值：

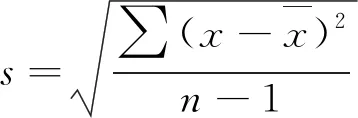
(1)

当样本容量较少时，也可用极差法按公式(2)计算总体标准差无偏估计：

(2)

式中，R为1组重复测定值极差；dn为与重复测定次数有关的极差系数，可从统计表中查得。

上述2个估计量也为随机变量。用公式(1)计算的总体标准差估计值的精度即标准差的相对标准差优于公式(2)估算精度[9]。

综合考虑总体标准差估计值计算准确度，当n<7～10时，用公式(2)计算总体标准差估计值简单方便，当n>10时则用公式(1)计算，准确度较高。

2.1.2 多样本等精度联合试验法

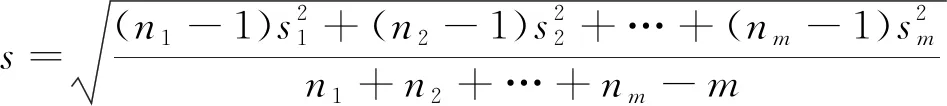
(3)

根据统计学原理按此公式估算方差的自由度：f=m(n-1)。

通常考虑使用多个样品在相同条件试验，可获得比单样品试验更准确可靠稳定的精密度估计值。

当n=2时，简称为双样试验法，公式(3)简化为：

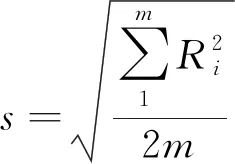
(4)

根据统计学原理按此公式估算的方差自由度：f=m。

同理，也可根据极差法按公式(5)计算总体标准差无偏估计值：

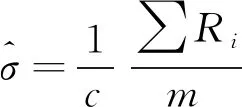
(5)

式中，c是m组极差平均值转换为标准差的系数。

根据统计学原理，按此公式估算方差的当量自由度：f=0.9 m。

国家标准和国际标准[2-3]中取c=1.128 38，1/c=0.886 2，即相当于m→∞、n=2情况，按公式(5)有：

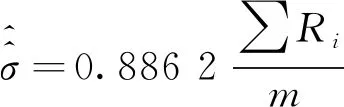
(6)

国际上制样精密度估算一般采用以下2种多样本等精度联合试验法：① ASTM D2013附录A.2指出，制样精密度估算需进行六组试验，每组5个煤样，每个煤样分成4份，重复测定4次。每个煤样按公式(1)获得1个方差值。按公式(3)计算每组平均方差的平均值和各组方差的平均值，若各个方差和各组方差符合规定要求，取六组平均方差的平均值作为制样精密度的估算值。② ISO 13909-7和GB/T 19494.3采用多样本双样试验法，连续进行两组试验，每组10个煤样，每个煤样重复测定2次，组成1对双样，获得1个极差值，按公式(4)或公式(6)计算每组方差并以此作为制样精密度的估算值。显然从实验样本量来看，按ASTM D2013获得的制样精密度值更精确。

2.2 制样精密度试验步骤

(1)制样系统预备检验。在精密度试验前，安装过程中或安装完成后应对有关设备性能参数进行检验，如各级破碎机出力和出料粒度，定质量缩分器或变比例缩分器调节性能、缩分比的稳定性、缩分器开口尺寸、切割速度等进行核查；安装完成后，制样系统应进行调试，并达到如下要求方可进行精密度试验。① 足够牢靠，能够在规定煤质条件(水分、粒度)、现场环境条件(温湿度、电磁场、粉尘)、设备工作条件下连续稳定运转，运转时无堵塞，很少进行维护或维修；② 操作安全，安全性符合现场安全规程要求；③ 制样过程中煤样残留少，通过清洗、吹扫、抽吸等避免试样污染；④ 制样过程中水分和煤粉损失少，且试样不产生明显的物理化学特性变化。

(2)准备试验煤样。选择日常主要用煤或日常用煤中变异性最大的煤作为试验用煤。从同一来源的一批或几批煤中，收集20个以上煤样，注意各煤样的粒度特性和灰分应大体相近，每个煤样的质量大约相当于预计的双份试验煤量，并将煤样破碎到全自动制样系统例常试验相同的粒度。

(3)连续进行双份试验。双份试验时，每次试验用煤量应接近制样系统单次标称制样量的上限，若制样系统中有变比例缩分器，应考虑调整该缩分器在最小缩分比的条件下工作。用二分器法或堆锥四分法从每个试验煤样中缩分出2个双份试验子样。对每个煤样按拟检验的制样程序重复试验，每个煤样获得1对一般分析试样，前10个煤样为一组，后10个煤样为另一组。分别化验灰分和空气干燥水分，得到1对干基灰分极差值。

(4)汇总试验结果。按公式(4)或公式(6)计算每组标准差值。试验应注意2个方面：①制样系统中有变比例缩分器，应将缩分比值调整到下限值；②双份样试验中的第2个试验煤样不能使用第1个试验煤样使用规定流程制样后除一般分析试验煤样(约100 g)外的全部弃样，因该样的粒度特性与原试验煤样显著不同，必定会影响试样结果。

3 精密度目标值或期望值确定

3.1 GB/T 474和ASTM D2013的规定

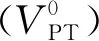
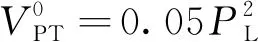
(7)

式中，PL为在连续采样时1批煤测定结果精密度估算值，该值可从国标GB/T 475—2008查到。

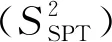
(8)

按照国标推荐的采样方案，一批煤采样精密度期望值(以干基灰分表示)在0.8%～2%，可推算出制样和化验总方差目标值处于0.04～0.2。

3.2 GB/T 19494.3和ISO 13909.7的规定

国际标准ISO 13909.7—2016和国标GB/T 19494.3—2004均未明确给出具体的制样精密度目标值，但给出了以下2种确定方法。

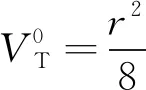
(9)

式中，r为灰分分析试验方法的重复性限。r可从GB/T 212查得，但在最坏情况下单个制样(缩分)阶段的方差不大于0.08。

整个制样系统制样和化验总方差目标值可按公式(10)确定：

式中，x为制样流程阶段数。

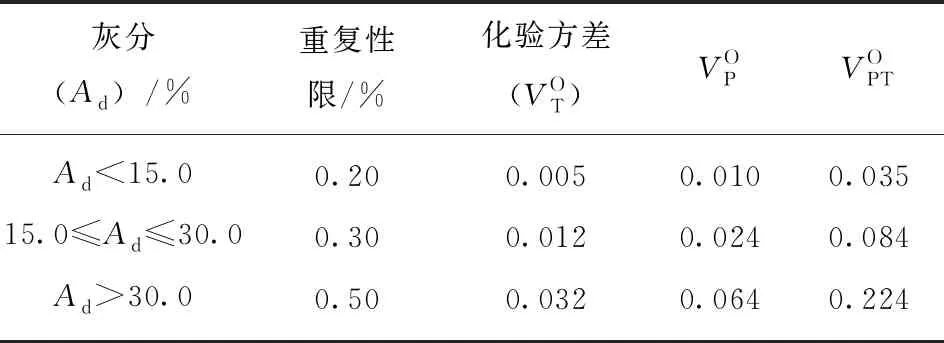
表1 制样和化验程序总方差目标值

(2)采用标准推荐的制样程序，在煤样缩分后留样量满足要求的条件下，以灰分表示的整个制样和化验总方差应不超过0.2。对于大多数煤来说，特别是当机械缩分器缩分煤样时的切割数高于规定值时可能获得更低的方差值。

按此规定，制样和化验的总方差目标值不与采样精密度和制样流程挂钩，也没给出具体值，但规定了制样和化验总方差目标值的最大值。

3.3 制样系统精密度目标值或期望值推荐

相较而言，ISO 13909.7—2016和GB/T 19494.3—2004对制样系统精密度目标值要求不超过0.2，此规定过于笼统，在实际中不便于操作；如按标准规定使用公式(10)所述确定的精密度目标值又不太合适，对于煤灰分Ad>30.0时偏大，而煤灰分15≤Ad≤30.0时显著偏小，同时与ASTM D2013和GB/T 475—2008规定的公式(7)也有所差别。

采用公式(7)确定制样和化验程序精密度目标值直接与采样精密度挂钩是正确的，其计算值也属恰当合理，实际执行时不会引起混乱，特别对于采样精密度要求较高时可合理控制制样误差。

对于某个制样(缩分)阶段方差目标值，可在制样和化验程序总方差目标值确定的条件下，按比例分解。例如，已知1批煤采样精密度期望值为1.6%，则其制样和化验程序总方差目标值为0.128，对于全自动制样系统该四阶段制样和化验程序，其各制样阶段和化验方差按2∶2∶2∶1分配，分别为0.036、0.036、0.036、0.018。

4 制样精密度合格判定

4.1 精密度判定的统计学原理

精密度试验所获得的方差估计值属随机变量，只有无数次试验结果才是试验条件下的精密度值。在实际试验中，样本数目应在60以上方可认为方差估计值的误差可忽略不计。但在小样本试验中，方差估计值的误差较大，不能将实际制样和化验方差值直接与目标值进行比较从而作出是否一致的判断，而应采用数理统计学中的χ2检验法进行判断[14-17]。

对于重复测定2次时的统计量χ2=ms2/σ2服从自由度为f=m的χ2分布，式中s2按公式(4)计算。

按χ2检验原理，作双侧检验其接受域为：

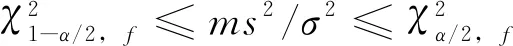
(11)

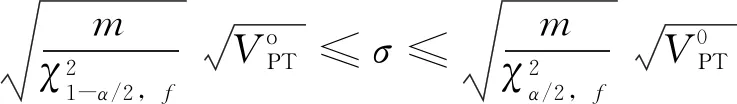
(12)

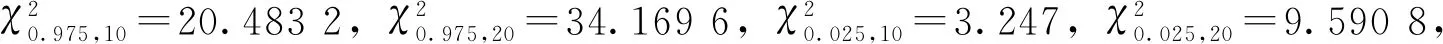
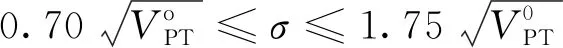
(13)

当m=20时，标准差置信范围按公式(14)计算：

(14)

从防范统计检验的风险考虑，自由度越大越好，一般自由度m应大于10。

4.2 精密度判定方法

4.2.1 直接比较法

由于实际试验为有限次，从统计学原理分析，较为精确的判定方法当属统计检验法。

4.2.2 国家(国际)标准法

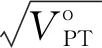
(15)

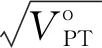
4.3 关于检验结论可靠性的讨论

为了提高检验结论的可靠性，国家(国际)标准规定了精密度判定公式(15)，同时又规定了精密度试验应连续进行两组，如果两组试验结论相同，则可作出最终结论。但若两组结论不同则如何作出最终结论以及如何处理，标准没有给出答案。笔者认为，在连续两组检验结论不同的情况下，首先应检查确认制样系统在设计制造和运行方面以及精密度试验过程中是否有问题，待解决问题后再重新试验。若无任何影响精密度的实质性原因，可按以下方法之一处理：

(1)加作一组试验，以三组中两组相同的结论作为最终结论。根据概率论中二项分布定理可推知，2次试验中，“结论相同”该事件的概率为0.9025，而3次试验中发生“不少于2次结论相同”此事件的概率为0.999 9。显然为了确认检验结论，在连续两组检验结论不同的情况下，如无其他原因，加作1次试验处理方式属于合理。

(2)直接将两组数据合并后处理，按一组20对数据进行χ2检验，仿照公式(15)即有公式(16)：

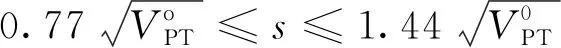
(16)

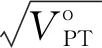
在两组数据合并之前应进行同质性检验，即用F检验法检验两组10个差值的方差是否具有一致性，用t检验法检验两组10对差值平均值是否具有一致性。

5 示 例

2)按国标法判断。① 按公式(4)计算2次制样系统制样和化验试验标准差分别为0.63、0.56，按公式(15)计算精密度目标值范围为(0.250、0.626)。② 由于2次试验有1次结果不满意，所以据此结果不能判定该制样系统精密度合格。③ 按公式(6)，按极差平均值计算2次制样系统制样和化验试验标准差分别为0.727、0.681，由于2次试验结果均不在范围(0.250、0.626)，所以据此可判定该制样系统精密度不合格。显然，同样试验数据采用不同的精密度估计公式计算值所得的结论不一致。

3)按文中建议给出试验结论。① 将两组20对试样的数据合并，按公式(4)计算制样系统制样和化验试验标准差为0.60。② 按公式(16)计算制样精密度目标值范围为(0.275、0.515)，故统计检验结论为：在95%置信概率下，制样系统实际精密度显著大于目标值，不合格。③ 按公式(7)通过极差平均值计算制样和化验标准差估计值为0.70，实际制样系统精密度显著大于目标值，不合格。

从以上计算也可看出，按极差平均值估算的标准差的偏大。

6 结论与建议

(1)煤炭全自动制样系统制样精密度试验方法可采用GB/T 19494.3和ISO 13909.7规定的多样本双样重复试验法，试验程序可按文中2.2所述进行。双份试样应是二分器法或堆锥四分法从每个试验煤样中缩分出的2个子样构成。

(3)煤炭全自动制样系统制样精密度与目标值或期望值是否具有显著性差异，可按GB/T 19494.3和ISO 13909.7规定进行判断。但当两组数据所得检验结论不一致时，应首先分析和查找原因，解决问题后重新试验。如未发现实质性的原因，可将两组数据合并后进行χ2检验，或增加一组试验，以三组试验中其中两组数据所得的相同结论作为最终结论。