基于POI动态推荐算法的融合时间序列分析

强蓉

（西南大学 重庆市 400715）

近些年，在实际应用中，大多会选择利用多种异构类型的上下文信息对不同用户的潜在偏好进行分析和挖掘，并为用户生成推荐列表，本文的研究提出一种融合时间序列的POI 动态推荐算法[1]。

1 基于用户的协同过滤算法与时间序列划分

在常规模式下，需要通过对不同用户访问情况的分析，来实现基于用户的协同过滤。这一模式下，需要分析、研究用户对相同位置访问的次数。并对不同用户之间的相似程度进行分析，即余弦相似度。协同过滤是一种十分经典的推荐算法，主要涉及到两个部分，即离线的过滤和协同的过滤[2]。分析协同过滤模型，通常情况下包含了若干用户和物品的数据信息。但是，评分数据并非存在于所有用户之间，其中仅有部分用户和数据间具有评分数据。而基于用户的协同过滤算法，通过引入一定的时间意识因子，综合各种地理位置信息进行分析，则可以构建起融合时间序列兴趣点动态推荐模型。

1.1 时间序列划分

在应用过程中，可以对时间序列进行不同的划分。在具体的划分方式上，有多种不同的情况[3]。例如，可以以小时为单位，将一天中的24 小时划分为24 个相等的时间槽。或者以天为单位，将每周7 天时间划分为休息日和工作日两个不同的时间序列。在本文的研究过程中，选择将一天划分为24 个小时。在不同的时刻，分别对用户相应的偏好情况进行分析。其中，时间t 代表了一定的整数，这些整数的取值范围为0~23。在对不同用户进行推荐的时候，在考虑用户喜好等情况的同时，也应综合考虑时间问题，结合不同时间段，为用户提供动态的推荐。而对不同时间段相似度度量的比较分析，可以掌握用户当前的时间信息，之后，便可以更为精确的为用户进行动态推荐。

通常情况下，用户在兴趣点访问方面的偏好与时间相关。因此，在不同的时间点，不同的兴趣点会对应具有不同的流行度。因此，对时间之间的关系进行分析有利于更好的对用户的喜好情况进行分析和描述。

1.2 时间序列度量方式

本文在应用基于用户的协同过滤算法时，应用时间序列对其实施了一定的改进。在从相似性角度对不同用户进行分析的时候，时间序列特征是十分重要的观察内容。假设不同的用户处于相同的时间范围内，但对同一个位置的访问频率存在一定的差异或者存在较为相似的情况。那么，则说明用户间所具有的相似度相对较低或者相对较高。具体进行分析的过程中，可以使用余弦相似度来衡量不同用户之间的相似度，计算公式如下所示：

在对不同时间序列相似性进行分析的时候，可以借助对全部用户任意两个时间点间相似度统计结果来进行判定。将收集到的相似度统计结果处理后获得平均值，即得到最终的统计结果，可用来进行相似度判定。具体情况如下述公式所示：

但是，在实际统计计算过程中，会出现一些孤立的时间点。这些时间点的存在会影响到最终的评估效果，降低了推荐效果。为此，还需要进行应的过渡处理。在进行处理的时候，可以选用平滑技术。

在研究中，设定在某一个时刻，即t 时刻，用户对位置l 进行了一定的访问。那么，对这一情况进行相关预测，计算出评分结果的方法参照如下公式，其中，与当前t 时刻的跨度之间的距离用n予以表示：

1.3 综合时间流行度与地理影响因子的算法

1.3.1 基于地理因子的推荐算法

从分布规律角度进行分析可以发现，POI 的访问情况与幂律分布情况相符合。具体来看，表现为POI 间距离越小，对应的用户访问的概率便越大。由此可见，在实际生活中，在兴趣点推荐领域，地理位置是一项十分重要的内容，会对相应的推荐效果产生很大的影响。在统计学中，幂律power law表示的是两个量之间的函数关系，其中一个量的相对变化会导致另一个量的相应幂次比例的变化，且与初值无关：表现为一个量是另一个量的幂次方[4]。例如，正方形面积与边长的关系，如果长度扩大到两倍，那么面积扩大到四倍。幂律分布是一种概率分布，在幂律分布中，事件发生的概率与事件大小的某个负指数成比例。也就是事件越大，发生的可能性越小。因此，在幂律分布中，小事件的数量要比大事件要多得多。幂律分布对两个兴趣点之间距离和用户签到几率之间存在的关系进行了描述，具体情况可以如下的公式进行表示：

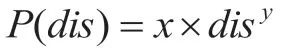
其中，dis 表示的为POI 之间的距离，P 代表的是签到POI 的概率。如果取对数，则可以得到如下的公式：

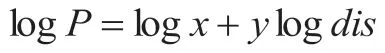
对其中的各项参数进行计算，计算方法采用最小二乘回归法。之后，可以选择应用一定的分类算法得出推荐结果。本次研究中，选择使用朴素贝叶斯分类法。朴素贝叶斯分类是一种十分简单的分类算法，在该算法的具体应用过程中，解决思路十分简单。在研究中可以设定特定的待分类项，之后，对此项出现情况下不同类别所出现的概率进行分析和统计，比较统计结果的大小，结果虽大的类别便为此待分类项所属的类别。在整个数据集中，利用P 来的表示全部的兴趣点集合，利用Pu 来表示用户已经访问过的兴趣点。那么，在计算用户未访问过的兴趣点P'的时候，其被用户访问的概率可以表示为：P( P' | Pu)。

如果现在前提条件是用户已经访问过Li，那么，在对其访问Lj的预测值进行计算的时候，综合应用基于地理影响因子所计算出的评分结果，可以采用的计算公式为：

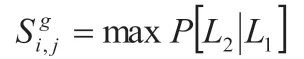
1.3.2 基于流行度信息的推荐算法

基于流行度信息进行计算的过程中，首先需要以时间为基础，掌握流行度特征的分布情况。为得到这一分布情况，还需要对在时间序列划分的基础上，处理各种兴趣点的流行度信息。之后，结合所获得的流行度特征分布情况，可以对用户对兴趣点的评分情况进行预测。具体来看，相应的计算公式如下：

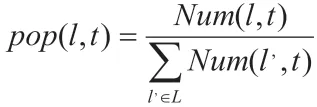
其中，所有的兴趣点集合用L 进行表示，在t 时刻兴趣点l 被用户所访问过的次数总和用公式中的分子部分进行表示。

将流行度信息与地理因子综合在一起，评分结果计算方法为：

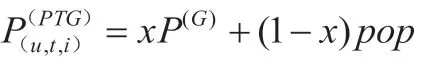
1.4 UTPG 模型与算法流程

建立UTPG 模型，假设某一个用户u 在某一个时刻（t 时刻）对l 进行访问。则相应的预测评分计算方法所参考的方式为下述公式所示内容：

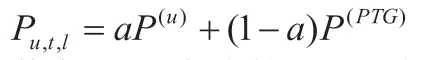
其中，a 所代表的是调节参数，其取值范围为0~1。

具体的算法流程如表1所示。

表1：算法流程

2 结果分析

2.1 数据集

在对本研究所提出的算法结果进行评估的时候，需要借助一定的数据集。在本文中，选择使用Gowalla 的用户签到数据集。在这一数据集中，会对不同用户的每一次签到情况进行相应的记录，并对其中涉及到的不同属性指标予以记录，包括用户的签到时间和用户ID 等。同时，还会涉及到一些地理位置相关属性指标，例如用户签到地所处的精度和维度等等。该数据集是一种真实、可靠的数据集，在兴趣点推荐领域的应用十分广泛。本文在应用这一数据集的时候，将其中20%作为测试集，其余80%的数据则列为训练集。

2.2 评价标准

衡量推荐结果的质量需要进行科学的评估，在进行结果评估的时候，本文选择使用召回率与精度这两个常用的指标。在对不同算法的应用效果进行评估的时候，算法所具备的覆盖能力是一个十分重要的观察指标。算法的覆盖能力越强，所对应的算法的应用效果越好。其中，召回率这一指标便可以用来对算法的覆盖能力大小进行评估，进而帮助人们更好的对算法的效果进行判定。在对不同算法的准确性进行评估的时候，大多会选择应用精度这一指标。在本文的研究中，在对推荐结果的质量进行评估和判定的时候，即选择使用上述两个指标。在计算精度的时候，应用的方式如下所示：

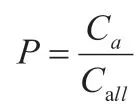
其中，Call与Ca代表的分别为全部集合与预测正确的集合。

在召回率进行计算的时候，计算方式如下所示：

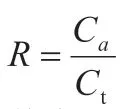
其中，Ct与Ca代表的分别为实际正确的集合以及预测正确的集合。

3 结束语

在本文中，综合考虑了4 种异构信息，提出了基于时间序列的POI 动态推荐算法。相关异构信息主要包括如下的内容：

（1）不同用户间偏好影响信息。这一类型的信息可以用来分析不同用户在偏好方面的具体情况；

（2）兴趣点时间特征信息。借助这类型的信息，能够实现对兴趣点不同时刻所具备的时间特征的分析研究。

（3）地理位置信息。对用户的不同访问兴趣点之间的关系进行分析，应用的分析方法为幂律分布函数。

（4）流行度信息。在研究中，通过对不同时刻不同兴趣点所具备的流行度信息进行分析，并将其融合到一定的算法当中，可以得到对用户访问兴趣点的预测信息，得出对应的预测概率结果。

另外，在实际生活中，进行兴趣点实践分析研究的时候，有时会受到现实条件等因素的影响，无法获取到充足的数据信息，进而影响到最终的推荐效果，降低推荐的精确性。而本次研究中所提出的推荐算法在改善推荐性能方面具有良好的效果，可以很好的应对实际生活中数据稀疏等问题，确保推荐结果的准确性。另外，通过本文的结果分析和验证也发现，研究中所应用的UTPG 算法在召回率以及精确度等指标方面均十分优秀，可以获得理想的推荐，具备一定的现实参考价值。