结合贪心策略的RGV动态规划调度模型

丁飞阳 张逸博 邱洪斌 陈勇

（浙江工业大学机械工程学院 浙江省杭州市 310032）

随着控制工程、信息技术、机电一体化等多个领域的快速发展，工业与新兴制造业开始向自动化、无人化、智能化发展，RGV（railguidevehicle）轨道式自动引导车作为一种集各种高新技术于一体可自主运行的系统，被广泛应用于现代化生产流水线中。RGV可用于各类高密度储存方式的仓库，其通道可设计成任意长。使用RGV 可以提高整个仓库储存量，并且代替传统叉车驶入巷道，使其安全性更高。RGV 的应用可以有效提高仓库的运行效率，并且可以十分方便地与其他物流系统实现自动连接，按照计划进行物料的输送。

如何合理调度RGV，提高 RGV 系统的运行效率，是促进制造业高速发展的一个重要问题。目前有刘丰瑞等人提出的基于各种模型而形成的高效率调度策略[1]；Liu YK 等人研究了RGV-CNC 系统的作业策略[2]；Dotoli M 和Fanti MP 研究了RGV 系统的死锁[3]；冯倩倩等人针对两道工序的调度问题，以CNC 任务分配和RGV 路径为决策变量，以物料剩余加工时间和RGV 状态建立了对应的数学模型[4]；江唯等人建立了以RGV 路径最短和移动过程中堵塞最少为目标的优化模型[5]；张明鹏等人以RGV 移动用时最短和RGV等待与工作时间最短为目标，得到了鲁棒性较好的调度策略[6]；徐晓龙得出了RGV 在CNC 加工一道和两道工序情况下的最优路径[7]。

针对本文相同或类似背景问题，也已经有许多人建立了各式的算法和模型。牛艺璇设计了混合编码粒子群优化的约束优化模型，虽然求解速度块，但是推广性差，对于更为复杂的调度情况其搜索精度会下降，容易陷入局部最优解或者无法得到可行解[8]；朱志斌等人设计了基于工序编码的粒子群算法，但是求解得到一个班次内的加工总数并不理想[9]；李昊哲基于对蚁群算法的优化，提出了优秀指标的概念，利用指标的归一化协助判定最优调度策略并构建了模型，但是模型中的RGV 无法在CNC 完成前或完成时到达上下料处，造成了时间浪费[10]；田继宏等人利用最短作业优先调度算法、遗传算法以及轮盘赌算法设计了模型，最后得到的调度策略中优先度仅依据单次作业执行的时间排序，在一些特殊情况下RGV 可能会比实际需求耗费多余的时间进行移动[11]；贾艳武等人使用最短路径法，根据线性规划建立了具有通用性的优化模型，但是在模型中出于清洗环节耗时相对较短而将其忽略了，导致最后调度策略与实际存在偏差[12]。

本文通过引入最短距离原则和尽快响应原则的贪心策略，对建立的动态规划数学模型进行改进，加速了解空间的搜索进程，在保证结果可靠性的同时加快了算法的求解效率，提高了模型的实用性。

1 问题描述及分析

本文研究的问题如下，有一个智能加工系统如图1所示，由8台计算机数控机床（以下简称CNC）、1 辆轨道式自动引导车（以下简称RGV）、1 条RGV 直线轨道、1 条上料传送带、1 条下料传送带等附属设备组成。RGV 的轨道两边等距分布四台数控机床。其中每台CNC 只能同时加工一个物料。RGV 根据指令能自动控制移动方向和距离，并自带一个机械手臂、两只机械手爪和物料清洗槽，两只机械手可各自抓取一个物料完成上下料作业，CNC 加工完成的熟料经过清洗放至下料传送带即视为加工完成。RGV 在上下料、清洗过程中均不能移动。本文研究在仅一道工序情况下使加工完成一定数量物料用时最短的RGV 调度策略。

图1：智能加工系统示意图

对RGV 工作流程进行分析，可以发现：除了最开始的阶段只需要给8 台CNC 上生料但不需要清洗环节，剩下的工作流程中，对于RGV 车而言始终都是上下料、清洗、等待（也可以不等待，即等待时间为0）、移动四个流程的不断重复，从而可根据每个成料加工完成的时刻将整个工作流程划分为一个个相似的阶段，每个阶段都是一个子问题。而这些子问题满足重叠性，因此可以尝试采用动态规划的数学思想在给定一个初始阶段的规划方案后对后续的调度进行规划，找到最优的调度策略。

2 建立动态规划数学模型

2.1 模型假设

（1）假设RGV 车前一阶段的状态只对相邻的后一阶段的状态产生影响，即无后效性。因为实际生产过程中有较多不可控因素无法被状态变量概括，从而使状态变量失去无后效性，导致动态规划模型失效；

（2）假设导轨两侧CNC 等距排列，间隔距离记为一个单位，且编号如图1所示；

（3）假设作业过程中RGV 车和CNC 均不发生故障；

（4）假设RGV 车移动过程不能中断。

2.2 符号说明

如表1所示。

表1：符号说明表

2.3 阶段划分

设需要加工n 个物料，由此前的分析，RGV 车始终都是上下料、清洗、等待、移动四个流程的不断重复且每个阶段都完成了一个物料的加工过程，从而可以将整个过程划分为n 个阶段。每个阶段内RGV 车都是完成上下料、清洗、等待、移动四个流程，如图2所示。

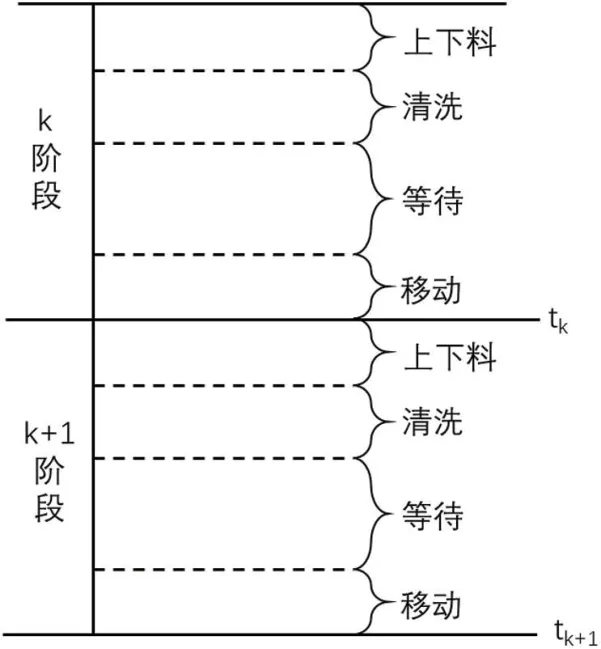
图2：加工阶段划分示意图

2.4 确定状态变量

对于每一个阶段，其状态就是这个阶段开始时RGV 所在位置以及阶段的起始时刻。这里不妨用RGV 车所在机床编号表示其位置。若RGV 车在第k 阶段开始时为第tk秒在i 号机床处，那么第k阶段状变量如下：

2.5 确定决策变量

这里用uk(sk)表示第k 阶段当状态变量为sk时的决策变量。RGV 车在完成清洗作业后经若干时长等待后可选择前往1 至8 号CNC 中的任意一个，即允许决策集合Dk(sk)={1,2,3,4,5,6,7,8}。各阶段决策确定后，整个问题决策序列就构成一个可行策略p1,n{u1(s1),u2(s2),…, un(sn)}。

2.6 确定状态转移方程

这里下一个阶段状态中RGV 车的位置就是上一阶段决策变量的值，起始时刻为上一阶段起始时刻加上一阶段所花时间。每一阶段所花时间为上下料及清洗作业时长、等待时长、移动时长之和。由此可写出状态转移方程如下：

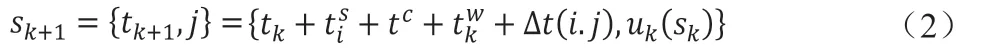
其中，表示RGV 车从i 点移动到j 点的所需时间，在本文所研究的情况下，RGV 车移动时间与移动距离有关，设tmx表示移动x个单位所需时间，Δ t(i,j)可写成如下表达式：

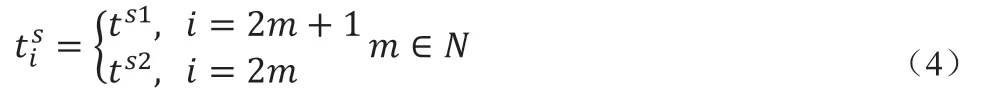
2.7 确定指标函数

设RGV 车在第k 阶段从sk出发，采用uk时的效益为：d(sk,uk)。由上述分析，这里的效益即时间，并且希望时间最短。因此d(sk, uk)为RGV 车在第k 阶段上下料、清洗、等待、移动所花时间之和：

设V1,k(sk, p1,k)表示从初始阶段到第k 阶段采取策略p1,k下的时间，若fk(sk)表示从初始状态到第k 阶段状态sk所花的最短时间，则可得以下表达式：

设RGV 从第0 秒开始工作，所以f1(s1)=0。

2.8 最终数学模型

综上所述，以完成n 个物料加工时间最短为目标的动态规划数学模型如下：

3 引入贪心策略

上述模型理论上可以求解得到加工n 个物料用时最短的调度策略，但这是一个具有指数复杂度的问题[13]，求解时间实测在1 小时以上。实际应用中往往将调度求解耗时也算在工作时间内，尤其在中途发生意外需要重新计算调度策略时，花费大量时间求解得不偿失。因此需要找一种求解效率较高并调度策略相对较优的调度策略。

本文第二节已经将整个问题转换为一个多阶段决策问题，在每一个阶段能让RGV 根据当前CNC 状态、RGV 自身所处位置以及调度规则直接做出一个在大多数情况下都是最优的决策，是一个更加贴合实际情况的方案。为此基于贪心算法的思想，引入了对每一个阶段内的调度优化策略。

（1）最短距离原则：若当前有多个CNC 需要服务，则选择最近的服务。因为选择更远的会使RGV 移动使用的总时间增加，导致CNC 等待时间变长，使总体效率降低。

（2）尽快响应原则：若当前暂时没有需要服务的CNC，则前往最早完工的CNC 处。这个原则在多数情况下确实是响应最早完工的CNC 效率高。但出现以下情况：当最早完工的CNC 离当前的RGV位置很远，又有比较近的CNC 完工时间稍晚于最早的那个，在这种情况下选择最早完工的CNC 可能并不是最优解，在特定状况下先去最近的CNC 可使CNC 总等待时间减少。但在实际过程中由于上下料也是由RGV 处理，正常情况下两个CNC 完工时间差会大于CNC 的移动时间，因此这种情况比较少见，尽快响应原则仍然有效。

4 算法流程

4.1 初始状态的确定

当系统开始运行时，所有CNC 都没有熟料，即RGV 刚启动时的唯一任务就是分别给8 台CNC 上料。根据这一点，将启动后的这一段过程进行分析，采用排列组合的方式求出RGV 给CNC 上料的所有组合。

刚启动时RGV 位于1 号和2 号CNC 之间，显然应该优先给这两台CNC 中的一台进行上料，然后再去为剩余的CNC 上料，所以可得初始的组合方案数量为NUM：

4.2 算法流程

（1）对初始启动阶段排列组合生成初始调度计划，即通过排列组合的方式求解出初始8 个阶段的状态变量集合{s1, s2,…, s8};

（2）随机选取一个初始状态变量集合，根据“最短距离原则”求解出此种初始解条件下的所有可行调度策略；

（3）重复（2），找出所有可行的调度策略，完成第一轮调度；

（4）给定任意一个确定的成料数n，已完成确定数量的成料所需的总加工时间最短为目标进行优化得到完成此数量的成料要求的最佳调度策略pk,n;

（5）重复步骤（4），且规定每次要求的成料数不同，计算不同成料数的最优调度策略，比较这些策略，找到出现次数最多的策略作为最终的最优调度策略;

算法的流程图可见图3。

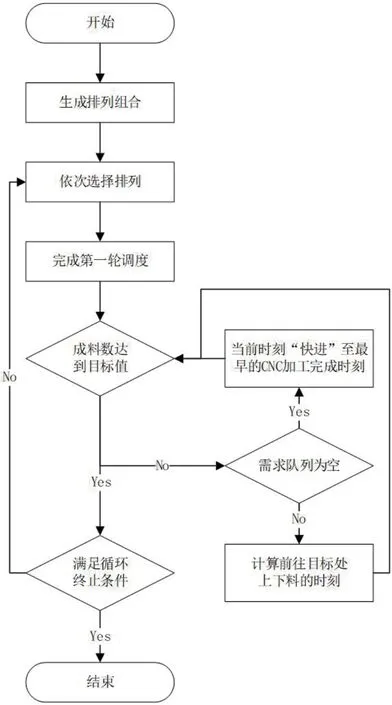
图3：算法流程示意图

5 求解结果与对比分析

5.1 MATLAB求解结果

本文采用2018年高教社杯全国大学生数学建模竞赛B 题中附件的相关数据，使用MATLAB 进行编程计算。得到的三组最优调度策略结果如表2至表4所示。

表2：第一组求解结果

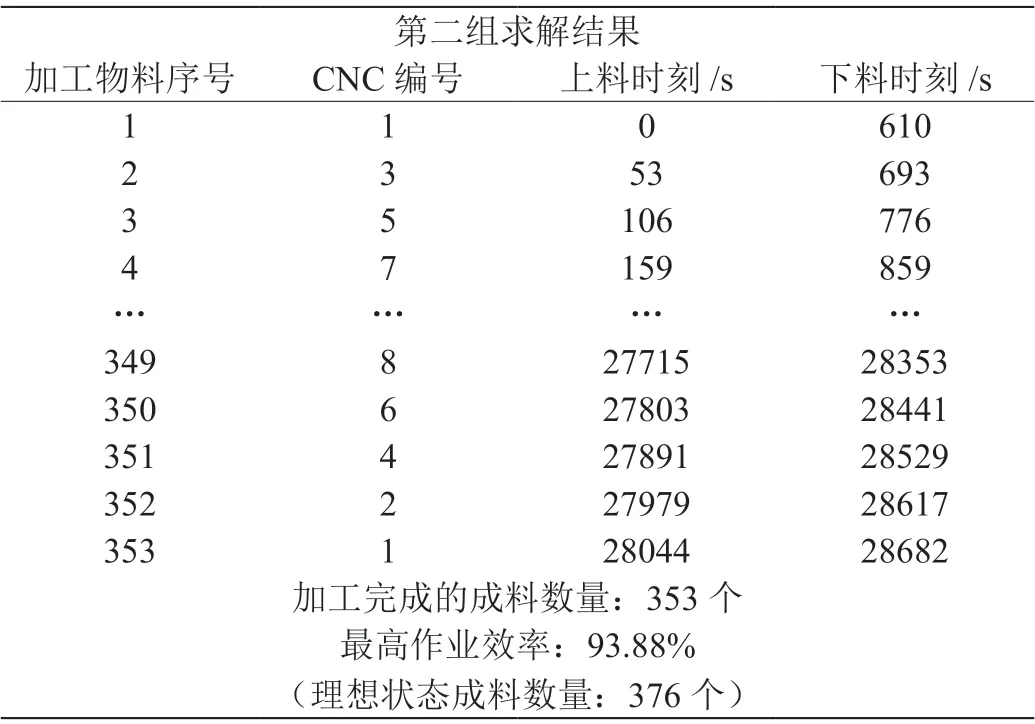
表3：第二组求解结果

表4：第三组求解结果

第一组调度结果中，最后剩余88 秒的加工时间未得到利用；CNC 加工顺序按照1 →3 →5 →7 →8 →6 →4 →2 进行循环。

第二组调度结果中，最后剩余188 秒的加工时间未得到利用；CNC 的加工顺序同第一组，按照1 →3 →5 →7 →8 →6 →4 →2进行循环。

第三组调度结果中，最后剩余52 秒的加工时间未得到利用；CNC 的加工顺序依然按照1 →3 →5 →7 →8 →6 →4 →2 进行循环。

综上可得，通过该模型和算法流程得到的8 台CNC 最佳调度策略，是按照1 →3 →5 →7 →8 →6 →4 →2 的策略进行循环加工物料。

5.2 计算结果对比

史爱武等人也基于贪心算法设计针对相同问题的调度算法[14]，他们通过不断寻找局部最优解来企图获取全局最优；潘舒曼等人结合动态调度，设计了纯贪心和基于二分图的贪心算法[15]。将上述两种模型的求解结果和重复10000 次的蒙特卡洛仿真得到的平均结果与本文的计算结果进行对比，详见表5。由此表对比结果可知，本文提出的模型得到的RGV-CNC 调度方案效果更好。（本文利用Anylogic 仿真软件实现蒙特卡罗仿真实验，详见图4和图5。

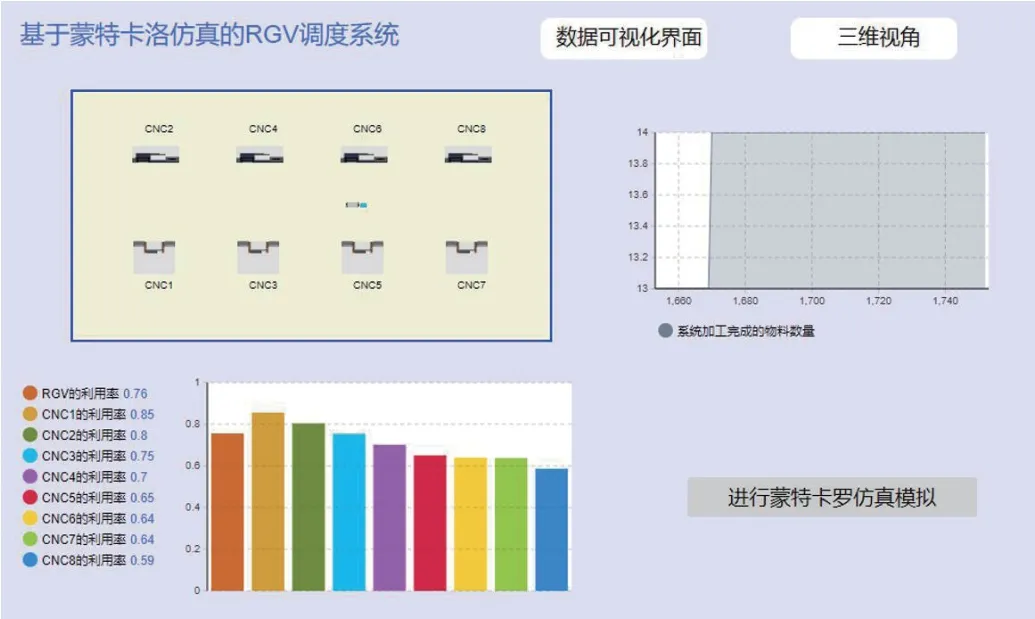
图4：Anylogic 仿真模型运行过程示意图

图5：Anylogic 仿真逻辑示意图

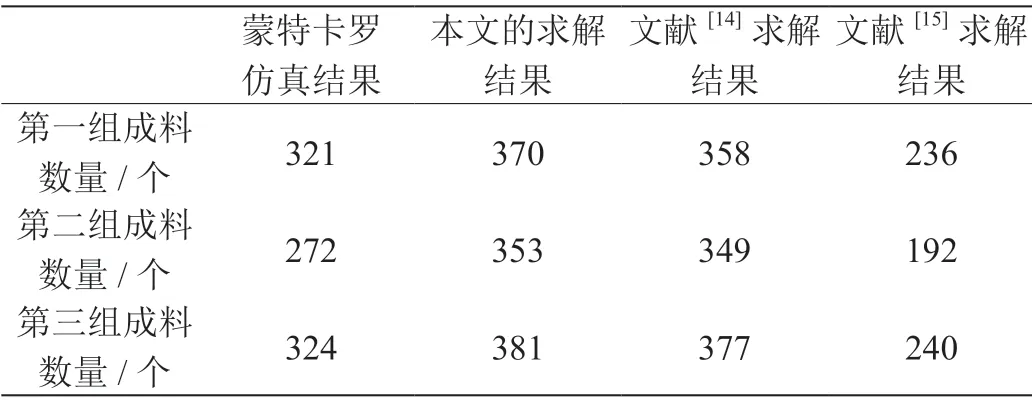
表5：求解结果对比

6 结论

本文针对一道工序的RGV-CNC 调度问题，基于贪心策略和动态规划思想，建立了RGV 动态调度的优化模型。将本文的计算结果与其他使用同一数据集的论文结果以及蒙特卡罗仿真结果进行对比，优异的表现验证了本文所建立模型的实用性。

目前国内智能车间布局逐步普遍，本文的研究对于RGV-CNC系统的动态调度策略的制定具有一定的实际参考意义。