基于改进型混合粒子群算法的船舶航向控制

胡春洋 胡杰 贾文鹏

（中船航海科技有限责任公司 北京市 100070）

目前航运业在全球经济一体化影响下发展的朝气蓬勃，由于船舶的自身运动惯性较大，时滞性强，加之在海上航行时，风、流和浪对船舶航行的干扰是无规律的导致航向不易控制[1]。为解决上述问题，PID 控制算法应运而生。其控制简单，控制效果好，应用广泛。但PID 参数整定需要按照方法查各种表，还要根据建立的数学模型做人工调整[2]。这个过程需要反复调整，时间较长，而且最终得到的很可能也不是最优的参数[3]。如果输入的变量很多，那么调节的可能性组合就会随之变多，这个工作常常不是非专业人士所能胜任的[4]。

粒子群优化算法可以不需要知道内部原理来调整PID 参数，而且调整的思路是朝着参数最优的方向进行，寻优速度快，所得结果精度高[5]。但是标准粒子群算法易陷于局部极值，针对此问题，很多学者提出了各种改进型粒子群算法。任子武等[6]在算法中引入变异因子，对每次迭代过程中得到的最优粒子进行变异，使其跳出局部最优；金翠云等[7]考找出每次迭代中位置最差的粒子，对其位置值进行更新，防止陷入局部最优；南杰琼[8]利用正弦变化规律来动态调整粒子的惯性权值，在搜索初期加大粒子群的全局搜索能力。改进型粒子群优化算法的目的都是为提升粒子的全局搜索能力，加快了粒子群优化算法的收敛速度为目标。

1 船舶运动数学模型

实际中船舶运动数学模型比较复杂，需要综合考虑舵机、舵、风、流等因素，得出非线性模型。为简化计算，便于研究，本文以野本数学模型作为船舶模型进行航向控制研究[9]，该模型将复杂的非线性模型化简为较为简单的一阶数学模型，如式（1）所示。

野本把船舶的转向运动看成是一个大质量物体的缓慢转首运动，因此船舶的转向运动方程可以用一个惯性环节来表示，式（1）中T 称为稳定性参数；K 为回转性参数，这两个参数可以通过船舶的“Z”形试验测得。

2 改进型混合粒子群算法

粒子群优化算法(PSO)是一种利用种群进化理念形成的一种计算技术，最初源于对鸟群捕食行为的研究。该算法的核心思想是利用群体中粒子的相互协作，共享信息，不断趋向食物，从而得到最优位置值。

粒子群算法将粒子模拟为鸟群中的鸟，朝着食物前进，不断更新粒子的速度和位置，粒子间也会进行沟通交流。每个粒子会把自己所经过位置的最优值记录下来，通过和种群中其他粒子的最佳位置值进行对比，得到相对最佳位置值，然后根据该值进行自身的速度优化和位置优化，继续朝着最佳位置前进[10]。在整个过程中，粒子不断调整自己的位置和速度，去趋向食物所在的方向。粒子通过下面的公式来更新自己的速度和位置。

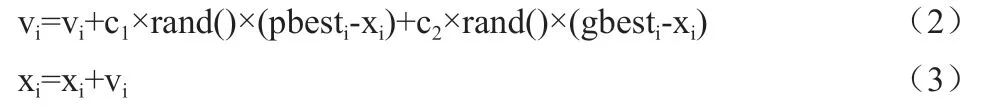
在公式（2）和（3）中，i=1,2,3……N，N 是此群体中粒子总数；vi是粒子的速度；rand()是介于（0,1）间的随机数；xi是粒子的当前位置；c1和c2是学习因子；vi的最大值为Vmax（大于0），如果vi＞Vmax，则vi=Vmax。公式（2）由三部分相加得到，第一部分为粒子的自身惯性，保留上次的速度值；公式（2）的第二部分为粒子最优值，表示粒子已运动过的位置记录，是目前得到的粒子的位置最优值；公式（2）的第三部分为社会因子[11]，是整个粒子群中的位置最优值，粒子间通过相互交流分享比较，得到了整个种群的最佳位置，代表粒子群的运动方向和趋势。由于公式（2）易陷入局部最优，需对其进行改进，改进后如下式所示：

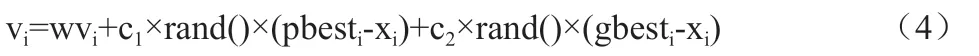
其中，w 为惯性因子，其值为非负。若其值较大，则全局寻优能力强，局部寻优能力弱；若其值较小，则全局寻优能力弱，局部寻优能力强。粒子群算法在迭代的过程中部分粒子有时会反向运动，这是由于粒子的惯性速度过大导致的，在迭代点附近，如果惯性因子过大，会导致很长时间无法收敛到一个点，同时也很难找到相比上一次迭代更优的解。为了解决该问题，本文采用随着迭代次数增加减小惯性因子的策略，如下式所示：

式中，i 为当前迭代次数，n 为总代数。将式（5）应用到式（4）中，增强了粒子的全局和局部搜索能力。

同时，继续对标准粒子群算法进行改进，将社会因子分解为了两部分——局部社会因子和全局社会因子，如下式所示：

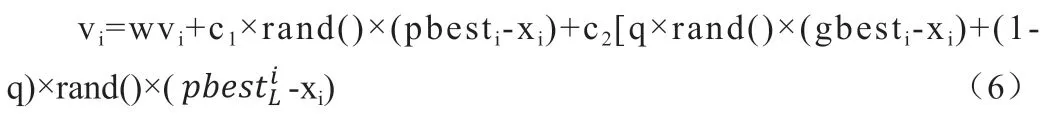
全局社会因子代表粒子的速度矢量向全局最优解方向运动，而局部社会因子则代表该粒子在局部范围内在朝着最优的方向运动，是该粒子一定范围内的最优解，一般这个范围是固定的，而包含的粒子数量（如果为1，则是粒子本身）不确定。

式（4）和式（6）的区别在于，式（4）收敛速度快，但是对于多极值问题容易收敛到一个局部最优解；式（6）由于要计算局部最优解，导致收敛速度相对较慢，但可以很好地解决式（4）收敛到局部最优解的问题。

3 PID参数整定

确定参数整定过程中的评价函数，本文选取绝对误差时间积分（ITAE）指标PID 控制器的性能评价指标，如式（7）所示：

式（7）中，Jmin越小，代表系统性能越好。

基于改进型混合粒子群算法的船舶航向控制原理图如图1所示。

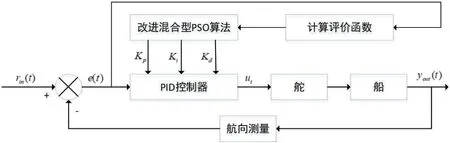
图1：MPSO-PID 控制算法原理图

由图1可知，PID 控制算法为：

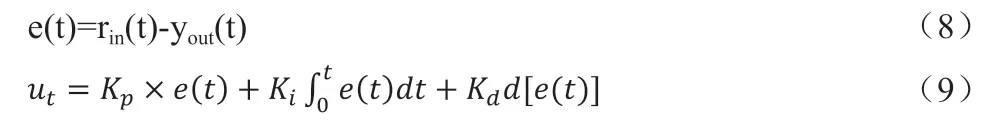
e(t)为输入与输出之间的误差，ut为控制对象的输入，t 为时间常数。

对PID 参数的寻优，就是利用本文提出的算法对式（7）求最小值的过程。其中粒子的位置信息代表PID 三个参数值，寻优的过程中，每次迭代都会产生一组最优的粒子位置信息，该信息中包含了单个粒子的最优值和整个种群的最优值，算法的不断迭代就是寻找最优值的过程。在整个寻优过程中，当求得式（7）的最小值或达到终止条件时，会产生一个相对位置最佳的粒子，该粒子的位置值即代表了PID 参数的最优值。

Step1：初始化粒子群，设置迭代次数，种群大小，飞行速度限值[Vmin, Vmax]，位置限值[xmin, xmax]；

Step2：将初始化的粒子的位置值作为粒子的最优值，计算每个粒子的评价函数值，得到最小的J 值，并将其作为全局最优值；

Step3：根据公式（5）计算粒子的权重值，并带入式（6），计算得到粒子的速度值；

Step4：将式（6）得到的结果带入式（3）中，得到粒子的位置值，如果粒子的速度vid＞Vmax, vid=Vmax；vid＜Vmin，vid=Vmin；xid＜Xmin，xid=Xmin；xid＞Xmax，xid=Xmax；

Step5：更新完粒子的位置和速度值后，将每个粒子的位置值与Step2 中的pbest 比较，从而更新个体最优值；将每个粒子的最优值与Step2 中的J 值比较，从而更新全局最优值。

Step6：判断是否达到终止条件，否，则跳至Step2，继续循环执行，反之跳出循环；

Step7：达到终止条件时，得到全局最优粒子，该值的位置值即为全局最优PID 参数值。

4 仿真研究

采用MATLAB 仿真试验，对本文提出的算法进行验证。设置系数c1=c2=2，惯性权重取值wmin=0.3，wmax=0.9；粒子的初始位置设置为[0,0,0]，最大位置为[30,0.5,120]；迭代次数设为100，粒子的飞行速度取值范围为[-1,1]。选取“育龙”号为研究对象，控制对象的数学模型选取Nomoto 模型：

式中，∅表示船舶航向角，δ 表示舵角，T、K 为系统参数，K=0.42，T=261.73，结果如图2-图4所示。

图2：航向控制效果图

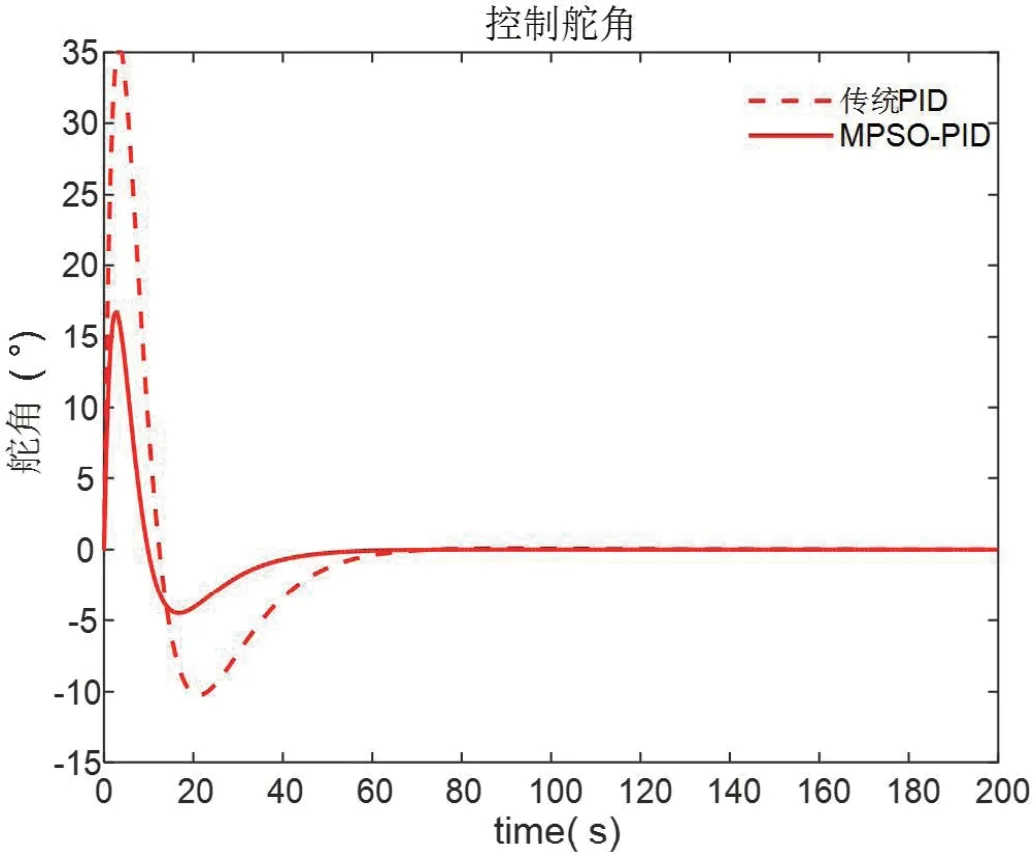
图3：控制舵角图

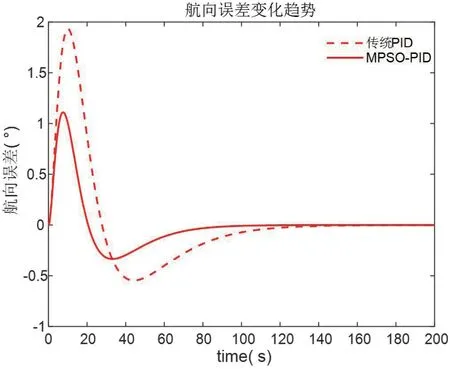
图4：航向误差图

5 结论

本文采用改进型混合粒子群算法优化PID 参数，将寻优后的控制效果与手工整定的控制效果进行对比，MPSO-PID 算法跟踪速度更快，控制精度更高，且无超调，打舵幅度更小，跟踪误差更小。证明了该算法的可行性与实际可操作性，无工程经验人员也可实现良好的控制效果。