双质体振动系统的周期运动与分岔特性

南向曈 邹烨

（湖南铁道职业技术学院 湖南省株洲市 412001）

含间隙和约束的机械设备在工作时会产生机械振动，引发机构不同部件之间及设备与地面、墙面之间发生机械碰撞，从而导致设备零部件的磨损及噪音的产生，影响设备运行可靠性及使用寿命。因此，对碰撞振动问题的研究存在重要应用价值，双质体冲击振动成型机就是一类典型的碰撞振动设备，对其振动问题的研究具有一定的代表性。目前多采用系统动力学方法，将机械设备简化为含间隙的振动系统动力学模型，进而研究其碰撞振动特性，进行动力学优化设计。冲击振动系统的非线性动力学研究对于具有冲击振动和运动限制约束的机械系统动力学性能优化和噪声抑制的匹配设计具有实际意义[1]。近几年各学者在相关方向持续作了深入研究[2-3]，侍玉青等用双参图呈现研究数据，分析含间隙振动系统低频周期冲击振动的模式类型及分岔特征[4]；张晓蓉等研究了两自由度赫兹接触碰撞振动系统在低频率、小间隙下存在的非完全颤振、迟滞区域共存等现象，得出高频下对称周期运动转迁到非对称的周期运动的变化规律[5]。

1 力学模型

将Hertz 接触理论与双质体冲击振动成型机的传统模型相结合，将振动系统两质体间的碰撞处理为弹性碰撞，并考虑碰撞面间的等效阻尼，以Kh表示两质体碰撞面间的刚度，Ch表示两质块碰撞面间的阻尼，得到该振动系统的简化非线性动力学模型如图1所示。

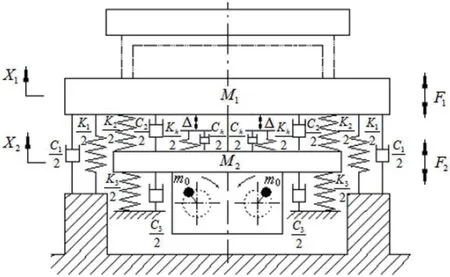
图1：双质体冲击振动成型机的弹性碰撞模型

图中其他参数的含义如表1所示，两质体间的碰撞条件为X2-X1=Δ。

表1：碰撞模型中各参数含义

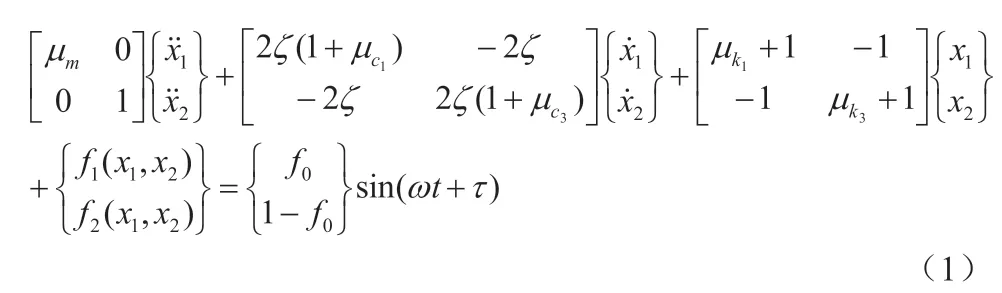
其中f(x1,x2)为两碰撞面间Hertz 接触力[6]的无量纲化形式，其具体表达式如（2）式所示。

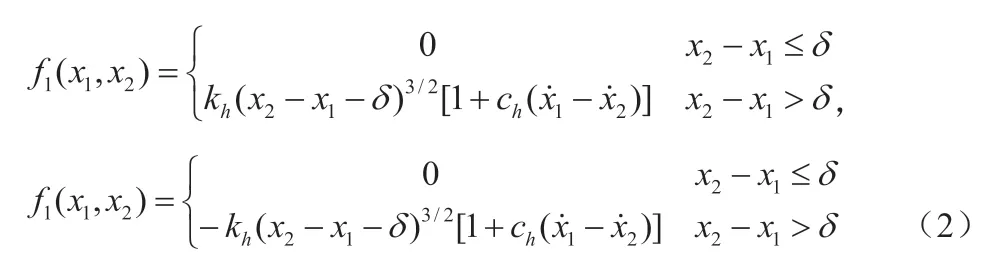
引入碰撞恢复系数R，由碰撞理论和动量守恒定律，两质体碰撞前、后的瞬时速度和满足：

2 Poincaré映射及分岔特性

取（5）式所示Poincaré 截面，并建立相应周期运动的Poincaré映射如（6）式所示。

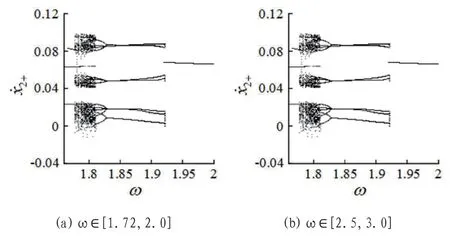
图2：局部分岔图

随激振频率ω 的增大，系统在ω∈[1.72,2.0]频域内由周期2 运动状态经历瞬间激变进入混沌状态，其后经历逆周期倍化分岔逐渐转迁到多周期运动状态，再经历瞬间激变进入稳定的周期1 运动状态，如图2(a)所示；在ω∈[2.5,3.0]频域内系统的运动特性类似，也是先处于混沌状态，而后经由Feigenbaum 逆倍周期序列由长周期多冲击运动状态逐步过渡到周期1 运动状态，其间依次经历概周期-周期8-周期4-周期2-周期1 等典型运动状态，如图2(b)所示。

借助相平面图观察激振频率ω=2.9 时系统的瞬时运动特性，对比两质体在这一碰撞瞬间的振动模式，如图3所示。可见质体M1的相图为一条封闭曲线，即处于周期1 运动模式，由右侧竖线可知质体M1在位移接近0.004 位置与质体M2发生碰撞，如图3(a)所示；此时质体M2的位移接近-0.02，且其碰撞后未直接进入下一运动周期，而是又经历了一次未发生碰撞的小幅振动，运动特性比质体M1丰富，如图3(b)所示。其对应速度随时间的响应图如图4，显然质体M1在相邻两次碰撞间只经历一次振动，从平衡位置一侧运动到平衡位置的过程中速度逐渐降到0，其后速度反向增大并向平衡位置另一侧运动，达到最大距离后返回，完成一次完整的振动，如图4(a)所示；质体M2则在对应两次碰撞间发生两次幅值不同的振动，如图4(b)所示，与图3分析结果相对应。

图3：ω=2.9 时两质体的相平面图

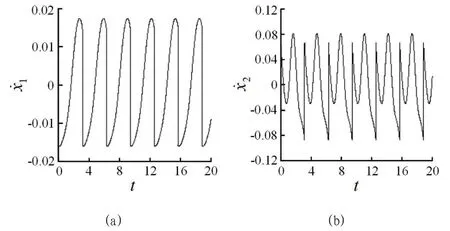
图4：ω=2.9 时两质体的时间历程图

图5所示为质体M2在不同外激励频率下的Poincaré 截面投影映射图，呈现出典型的混沌吸引子，可见此时系统处于混沌状态，两质体的碰撞振动特性无明显规律性。但随激振频率增大，混沌吸引子由图5(a)所示的整体聚集状态逐步过渡到图5(c)所示的三块聚集状态，预示系统由混沌运动向多周期运动的演化过程，与图2分岔特性相对应。

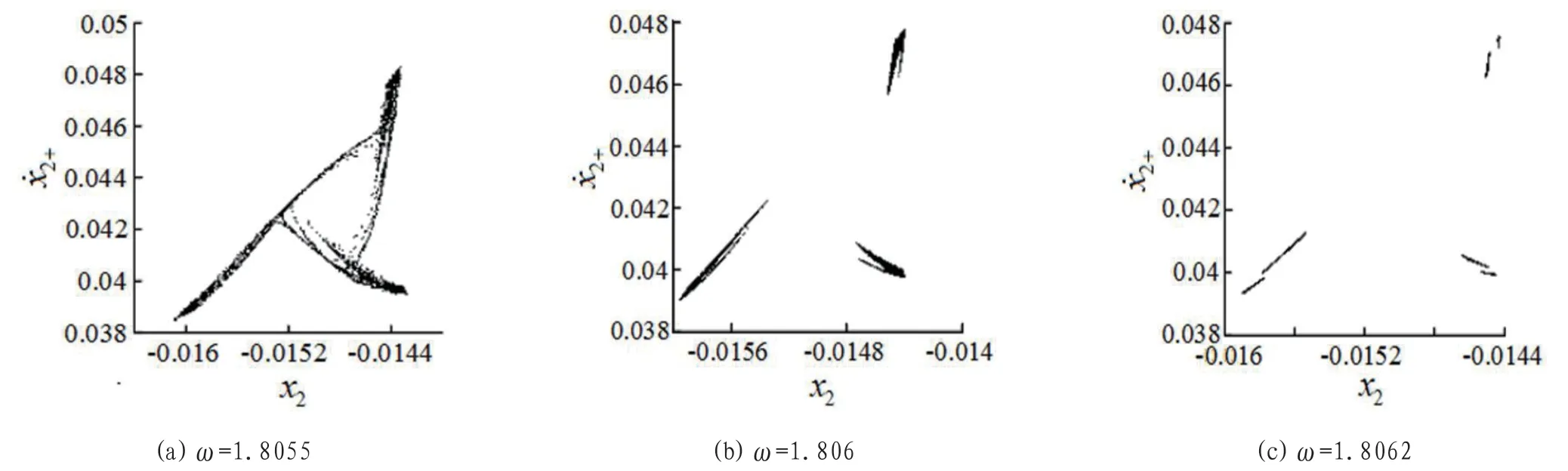
图5：混沌状态下的Poincaré 截面图

3 结论

文章对双质体冲击振动成型机的传统模型进行改进，引入Hertz 接触理论，将系统两质体间的碰撞关系处理为弹性碰撞，并同时考虑碰撞面间的等效刚度和阻尼对碰撞特性的影响。在所选基准参数下，揭示了系统在所选Poincaré 截面下的周期冲击振动模式及相应分岔特性。研究显示，系统在外激励频率ω＜3.0 频域内表现出复杂多样的非线性动力学特性，在混沌、瞬间激变、倍化分岔及其他多周期等振动模式之间相互转变，平稳的周期1 运动窗口很窄，两质体的振动模式均不稳定。