高中立体几何中多面体外接球的多维理论

钟景明

摘 要：立体几何是高中数学中的重要内容，而外接球问题不仅涉及到了球本身的性质，而且侧重考查学生对于内部几何体的结构与性质的理解与掌握，有力地考查了学生的学科素养.因此，近年来，该问题常常受到全国卷与省地区的命题者的青睐.针对该类问题的复杂性，笔者将从理论与题型这两个方面重点研究，提出一套完整的理论与相关的方法，促使理论与实践、经验与手段、题型与解法均可相互融合与促进，以达到教与学、学与用均可相得益彰.

关键词：多面体;外接球;多维理论;方法

研究高中立体几何，自然离不开平面几何的相关概念.平面多边形的外接圆，顾名思义，就是指“与多边形各顶点都相交的圆”。对于一个多边形，若其外接圆存在，则就只有一个，其圆心与半径是确定的，而外接圆的圆心自然到每个顶点的距离均相等。据此，我们对于立体几何中，外接球的定义就非常明朗。

一、立体几何中外接球的定义

定义  若一个多面体的各顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球。

显然，要解决外接球的问题关键是抓住外接的特点，即球心到多面体的各顶点的距离均等于球的半径。

二、外接球问题的多维理论

解决外接球问题，关键需要借助以下的相关结论：

结论一：数轴上，到两点A、B的距离相等的点就是线段AB的中点。

结论二：平面内，到两点A、B的距离相等的点的轨迹就是线段AB的垂直平分线（过AB的中点），简称为中垂线。

结论三：平面内，到不共线的三点A、B、C的距離相等的点就是△ABC的外心。

结论四：空间中，到两点A、B的距离相等的点的轨迹就是过其中垂线且垂直AB的一个平面，简称为中垂面。

结论五：空间中，到不共线的三点A、B、C的距离相等的点的轨迹就是过△ABC的外心且垂直于平面ABC的一条直线，简称为外垂线。

结论六：对于一般的三棱锥，其中两个三角形的外垂线的交点就是该三棱锥外接球的球心。

根据以上六个结论，不难看出，寻找外接球球心的关键核心就是弄清楚维度的变化与点数之间的递进关系.另外，确定球心位置后，所有求外接球半径最初或最终几乎都归结到三角形中的勾股定理.因此，我们需要熟知以下特殊三角形外心的若干题型与规律。

1.等边三角形的外心为其中心（四心合一）。

2.直角三角形的外心为斜边的中点。

3.锐角等腰三角形的外心在三角形内部，且在顶角的角平分线上，可由关系式：求出外接圆的半径r，其中L为底边长，h为底边上的高。

4.钝角等腰三角形的外心在三角形外部，且在顶角的角平分线上，可由关系式：求出外接圆的半径r，其中L为底边长，h为底边上的高。

5.对于给定任一边边长及其对角的三角形，则可由正弦定理求出外接圆的半径rv

6.针对结论六，对于一般的三棱锥，其外接球的半径可由以下公式（*）求出：

其中，l1、l2分别是三棱锥其中两个三角形的外接圆圆心到其交线的距离，L为交线长，α为该两个三角形所在半平面所形成的二面角的平面角大小。

特别地，若三棱锥有两个三角形互相垂直时，公式（*）则变为，其中，r1、r2分别是两个垂直的三角形的外接圆半径。

三、外接球问题的若干题型与解决方法

例1 （正方体或长方体的外接球问题）一个长方体的各顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为3、4、5，求该球的体积。

分析：易知，正方体或长方体的外接球的球心位于其体对角线的中点，

则半径，故该球的体积为.

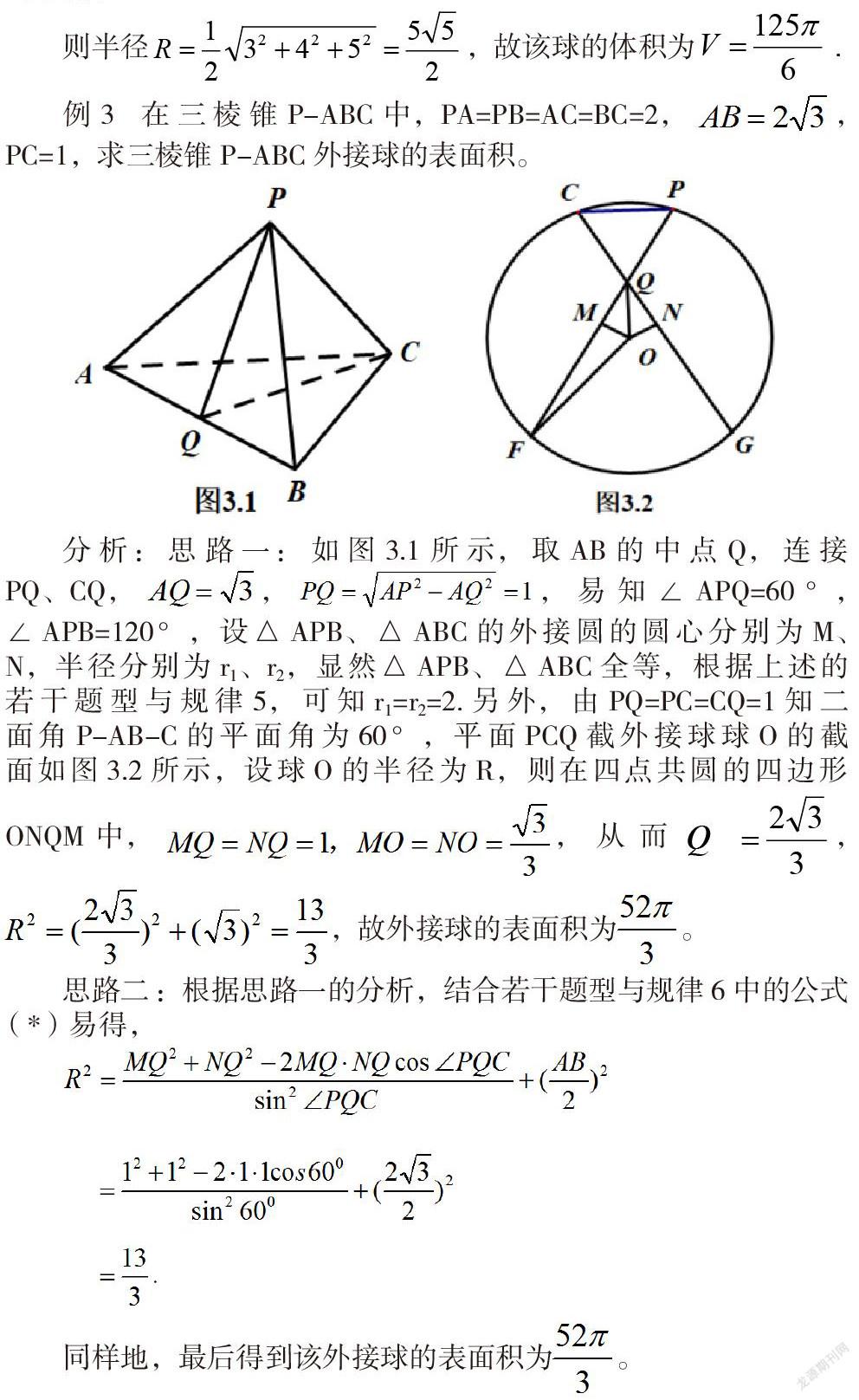
思路二：根据思路一的分析，结合若干题型与规律6中的公式（*）易得，

同样地，最后得到该外接球的表面积为。

事实上，思路二只是对思路一的高度概括与提炼，两者并没有明显的差异，都绕不开正余弦定理的应用。

解决该问题，关键核心还是“定心”，包括确定三角形的外心，或其他多边形的中心等，借助多维理论，不难确定出“球心”，最后往往利用勾股定理、正余弦定理求半径。该多维理论能够促使学生深刻而严谨地理解平面几何与立体几何之间本质上的联系，从而系统性、科学性、有效性地去掌握外接球问题。

参考文献：

[1]武增明. 确定简单多面体外接球的球心的策略[J]. 数理化学习：高中版， 2013（2）：8-9.

[2]苏旭景. 高中数学中外接球问题的解题策略[J]. 吉林画报（学术版）， 2013（6）.

1966501705250