基于逻辑表格法的水电站电气主接线可靠性分析

李鸿儒，杨文韬，朱志刚, 郭 宁

(1.中国电建集团昆明勘测设计研究院有限公司,昆明 650000；2.北京博超时代软件有限公司，北京 100000)

0 前 言

随着新能源的迅速发展，抽水蓄能电站的建设显得尤为重要，而抽水蓄能电站装机容量大，基本都需要对电气主接线可靠性进行评估。可靠性是指元件和系统在规定条件下和预定时间内，完成预定功能的概率[1]。水电站电气主接线可靠性是指在设计水平年(或规定时间)和规定条件下完成向电力系统发送或吸收预定电量的概率。可靠性分析的方法有很多，常用的主要有逻辑表格法、最小割集法、故障模式与后果分析法、蒙特卡罗(Monte Carlo)模拟法等[2]。

逻辑表格法由苏联学者于19世纪70年代提出，与其他方法相较，该方法比较简单直观、易于理解，也是较早应用于中国电力系统可靠性分析的方法之一，但由于该方法计算机程序不易编制，目前基本上处于手工计算阶段[3]。鉴于此，中国电建集团昆明勘测设计研究院有限公司与北京博超时代软件有限公司进行合作，基于AutoCAD进行二次开发，实现了适用于水电站、抽水蓄能电站高压侧电气主接线可靠性分析的逻辑表格法的程序化，并对分析所需的电气设备可靠性基础统计数据进行收集和整理，可提高工程设计中的工作效率。

1 逻辑表格法程序化

1.1 水电站电气主接线可靠性分析特点

DL/T 5186-2004《水力发电厂机电设计规范》中规定装机容量750 MW及以上的水电厂应对电气主接线可靠性进行评估。水电站电气主接线按电压等级可分为发电机电压接线和升高电压侧接线，发电机电压接线方式简单明了，易于判别可靠性。

水电站升高电压侧接线主要涉及的电气设备有断路器、隔离开关、互感器及避雷器等，隔离开关和互感器的数量较多，如果所有设备都被考虑，分析将变得相当复杂，通常采用把其他元件故障率合并到断路器的简化处理方法。考虑到隔离开关、互感器及避雷器故障率与断路器相差一个数量级[4]，本文中只考虑断路器、母线和送出线路的故障与检修情况。

1.2 逻辑表格法

电气主接线可靠性分析用的逻辑表格法，在文献[5]中有较详细的介绍，以连通性作为判据，根据电气主接线的接线方式，考虑单重及一个元件处于检修，另外一个发生故障的所有可能情况，将其发生概率及造成的停运时间一一列出，再根据所需的可靠性指标进行汇总，得到决策事件表。逻辑表格法依赖于接线方式，不易编程，不适合用于大规模的电力网分析，但能很好的用于元件数量不多，接线简单的网络，在水电站、抽水蓄能电站电气主接线可靠性分析中具有很好的适用性。

1.3 基础参数定义

(1) 平均故障率及检修率

故障率是指可修复设备在单位时间内的平均故障次数，用λ表示，单位为次/(台·a)。

平均检修率是指可修复设备在单位时间内的计划检修次数，用μ表示，单位为次/(台·a)。

(2) 故障平均停运时间及检修平均停运时间

故障停运时间是指为了发现和消除一次故障所必须的修复时间，用Tg表示，单位为h。

检修平均停运时间是指设备检修一次所需要停运的平均时间，用Tj表示，单位为h。

(3) 计划检修系数

计划检修系数是指设备处于计划检修状态的时间概率，按下式计算[5]：

(4) 计划检修时间

计划检修时间指1a内设备检修需要停运的时间，h/(台·a)。

1.4 断路器故障率修正

断路器的操作次数及故障率和与其连接的元件相关，由于统计所得的故障率是断路器的平均故障率，因此有必要采用合适的故障模型，对主接线中处于不同位置及不同运行条件的断路器故障率进行修正。

(1) 有出线的中间断路器

有出线的中间断路器指位于两个断路器之间且两侧分别连接有送出线路和发变组的断路器，其修正如下：

(2) 无出线的中间断路器

无出线的中间断路器指位于两个断路器之间且两侧都接有发变组的断路器，其修正如下：

式中：λx为修正后的断路器平均故障率；λp为统计的断路器平均故障率；Kj为断路器静态系数，一般取0.3；Kq为断路器切短路系数，一般取0.3；Li为送出线路长度，百公里；Lp为平均线路长度，百公里；Kc为断路器操作系数，一般取0.4；Np为断路器年平均操作次数，次/(台·a)，我国取24；Nc为高压断路器因机组的启停，每年增加的操作次数，次/(台·a)，当Nc难以确定时，可取Nc=Np；λG、λT及λGB分别为水轮发电机组、主变压器及发电机断路器平均故障率，次/(台·a)；λL为送出线路平均故障率，次/(百公里·a)。

线路侧断路器、主变压器-机组侧断路器修正详见文献[6]。母联断路器、分段断路器及联络变压器断路器故障率不做修正，取λp。

1.5 机组和线路停运时间计算

水电站、抽水蓄能电站作为电能输出元件，其电气主接线的始端为水力发电机组，末端为送出线路，其可靠性主要考核机组和线路的停运情况。造成机组或线路的停运的情况可按如下分类：

机组或线路的停运分为可通过配电装置倒闸操作即可恢复运行和不可通过倒闸操作恢复运行2种情况。倒闸有效时，设备停运时间为：

Tt=Tf+mTc

(4)

式中:Tf为运行维护人员发现故障时间，取0.3h；Tc为隔离开关操作时间，取0.1h；m为需要操作的隔离开关个数。

倒闸无效的情况，其停运可能由单个元件造成，也可能因2个元件引起。由单个元件造成的，如线路自身停运或与机组串联的设备停运，其停运时间取决于停运设备的修复时间Tg或Tj。因2个元件引起的停运指某个元件处于检修时另一个元件又发生故障的情况，该情况又分为2个元件的共同作用和双重作用2种，共同作用指2个元件同时停运才会造成不连通，2个停运元件中只要有一个被修复就可以恢复运行，其造成的停运时间为[5]：

双重作用是指2个元件中只要有一个停运就会造成不连通，只有2个停运元件都被修复才能恢复运行，其造成的停运时间为：

1.6 逻辑表格编制

用于可靠性分析的逻辑表格如表1所示。

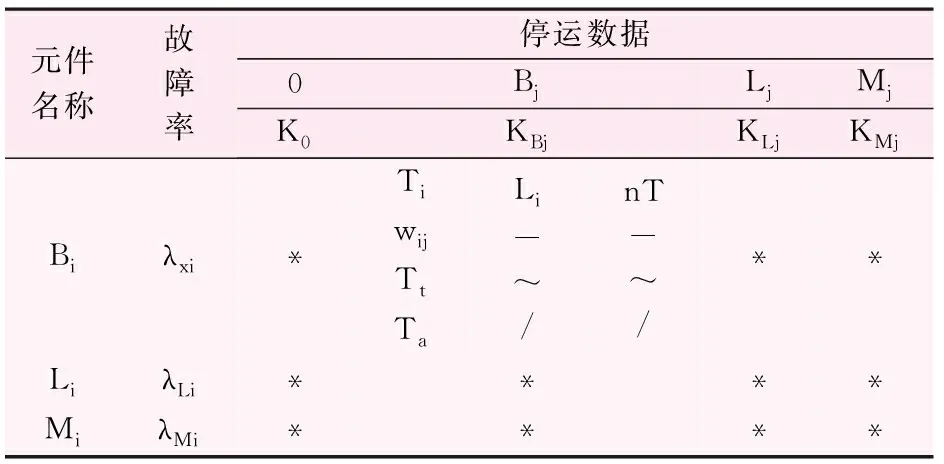
表1 逻辑表(i=1,2,3,…,n;j=1,2,3,…,n)

表中，第一列为故障元件名称，Bi、Li及Mi分别表示第i个断路器、第i回送出线路及第i条母线，需把所有考虑的断路器、出线及母线都列出；第二列为元件故障率，λxi、λLi及λMi分别表示第i个断路器、第i回送出线路及第i条母线的故障率；第一行为检修元件名称，Bj、Lj及Mj分别表示第j个断路器、第j回送出线路及第j条母线，需把所有考虑的断路器、出线及母线都列出；第二行为元件计划检修系数，KBj、KLj及KMj分别表示第j个断路器、第j回送出线路及第j条母线的计划检修系数；“0”表示没有元件在检修的情况，对应的状态系数(概率)为：

第j个元件在计划检修，又碰上第i个元件故障时，其造成的停运数据填写在第i行与第j列交叉的表格内，表1中只列出了Bj元件在检修碰上Bi元件故障时造成的停运数据，其余用“*”简化表示。

停运数据，第一行为停运设备名称，Ti、Li及nT分别表示第i个主变压器-机组单元、第i回出线及n个主变压器-机组单元同时停运的情况，需把所有需要考虑的停运情况列出；第二行为设备停运的频率，如wij表示Ti设备停运的频率，其值为[5]：

wij=λxiKBj

(8)

其余用“-”简化表示，如果有造成对应设备停运则填写，没有则不填；第三行为设备停运的时间，如Tt表示Ti设备停运的时间，其余用“～”简化表示，如果有造成对应设备停运则填写，没有则不填；第四行为一年内元件停运总时间，如Ta表示Ti设备一年内停运的总时间，其值为：

Ta=wijTt

(9)

其余用“/”简化表示，如果有造成对应设备停运则填写，没有则不填。

水电站、抽水蓄能电站内部双重故障出现机率较小，表1中未考虑双重故障，即2个设备同时发生故障的情况，如果进一步考虑双重故障，可对表格进行扩展，在表格第一、二行中增加故障元件名称及故障率，并在对应交叉表格中填写停运数据加入统计分析。

1.7 逻辑表格程序化

逻辑表格的计算机程序是基于VisualStudio开发环境，运用ObjectARX开发软件包对AutoCAD平台进行二次开发完成的，最终生成arx文件，加载到AutoCAD中进行使用。程序流程如图1所示。通过模型及参数输入流程可在AutoCAD中绘制用于可靠性分析的电气主接线简图及输入设备的基础参数。程序将根据电气主接线简图对断路器(CB)类型进行判定，并基于输入的基础参数对断路器故障率进行修正，接着对故障情况进行分析，并计算出机组和出线的停运时间，最后在Excel中生成逻辑表，并基于逻辑表汇总出决策事件表。有了决策事件表之后，其余可靠性分析用表是比较容易编制的，也可以根据不同的关注点，制作不同的比较用表。

图1 程序流程

程序流程中，机组和出线停运时间计算的关键是对故障影响进行分析，涉及到的一些基本运行规则如下：

(1) 元件处于检修状态时，元件本身不连通，但与检修元件隔离开的其他设备可以正常运行;

(2) 元件发生故障时，会跳开两侧所有的断路器，通过操作隔离开关把故障元件隔离后，跳开的断路器可恢复运行;

(3) 同一设备计划检修与故障不会重叠，对应的交叉表格停运数据不填写;

(4) 并联的元件，当其中的一个停运时，可以通过另外一个元件进行连通，所有的并联元件同时停运将造成不连通。

2 实例分析

2.1 设备可靠性基础统计数据整理

设备可靠性统计数据是进行可靠性分析的基础，目前采用逻辑表格法进行可靠性分析所基于的数据大多还是20世纪90年代的。文章对我国近些年发布的设备可靠性指标进行了收集，整理如表2所示。

表2 设备可靠性基础统计数据

表中，1992年的数据来自《水电厂电气主接线可靠性计算导则》，其中括号内为GIS设备数据，相应的括号外为敞开式设备数据；1995—1999年的数据来自文献[7]，文献未提供330kV的数据及母线故障平均停运时间；2001—2005年的数据来自文献[8]；2011—2016年的数据来自文献[4]和[9]；2017年的数据来自文献[4]。表2中的数据都是基于文献近似处理所得，近似认为故障率等于强迫停运率或非计划停运率(1992年数据除外)。关于强迫停运率和非计划停运率的定义详见DL/T837-2003《输变电设施可靠性评价规程》。

从表2中可以看出，相比过去，设备故障率已有明显降低。文章以时间较近的2017年可靠性统计数据进行的实例分析，发电机断路器λGB平均故障率取0.003次/(台·a)[10]，平均线路长度Lp取0.798百公里[11]。

2.2 电气主接线绘制

金沙江观音岩水电站装机定为5台600MW的混流水轮发电机组，发电机与主变压器连接采用单元接线，发电机出口装设专用断路器，主变压器高压侧电压等级为500kV，初期出线2回至仁和变电站，单回送出线路长度约84km，另备用1回出线，文中按相同的送电距离考虑。电站高压侧拟采用4串3/2接线、2串4/3和1串3/2接线及双母线接线3个方案中的一种，需进行可靠性分析比选。在开发的程序中绘制的电气主接线如图2～4所示。

图2 4串3/2接线(方案1)

2.3 结果分析

程序计算结果如表3所示，从决策事件表中可以看出不同方案下电站某台机组、某回送出线路或多台机组同时停运的概率和平均停运时间。表中 “停任一发变组”项包含了多台机组同时停运的情况，此时，电站送出容量将受阻，代表着电站的可靠性水平，是主要分析指标。从表3中可以看出电站高压侧接线采用方案2时，机组发生停运的概率和对应的停运时间最小，分别为0.0954次/a和0.0539h/a，方案1次之，方案3最差。

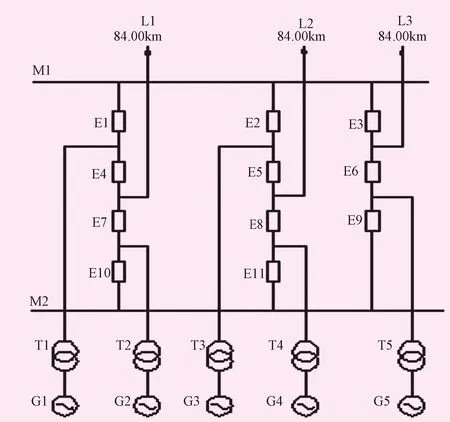
图3 2串4/3和1串3/2接线(方案2)

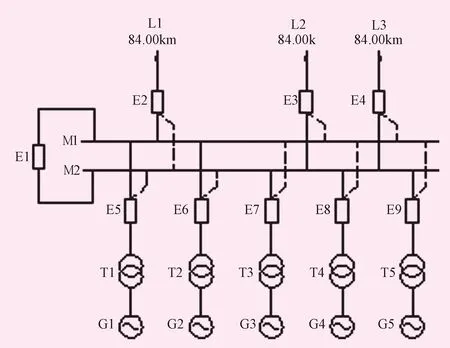
图4 双母线接线(方案3)

方案2相比方案1可靠性差别不大，但投入的断路器个数少一个，方案3可靠性最差，但投入的断路器数量最少，具体哪个方案最合适，需要把可靠性和经济性结合进行综合比较。

基于决策事件表并结合电站装机和送出线路情况可以得出包含受阻电量的指标汇总表，再结合设备投资和上网电价可以得出经济比较表，最后汇总出综合比较表。该部分内容在有了决策事件表后是比较容易编制的，且比较灵活，文中不再论述。

值得一提的是，可靠性分析结果除了跟接线形式有关，还与基础统计数据、送出线路长度及机组台数等诸多因数有关。相同的比选方案可能因送出线路长度不同，或是基于的元件故障率随时间发生了变化，分析结果都有可能不一样。

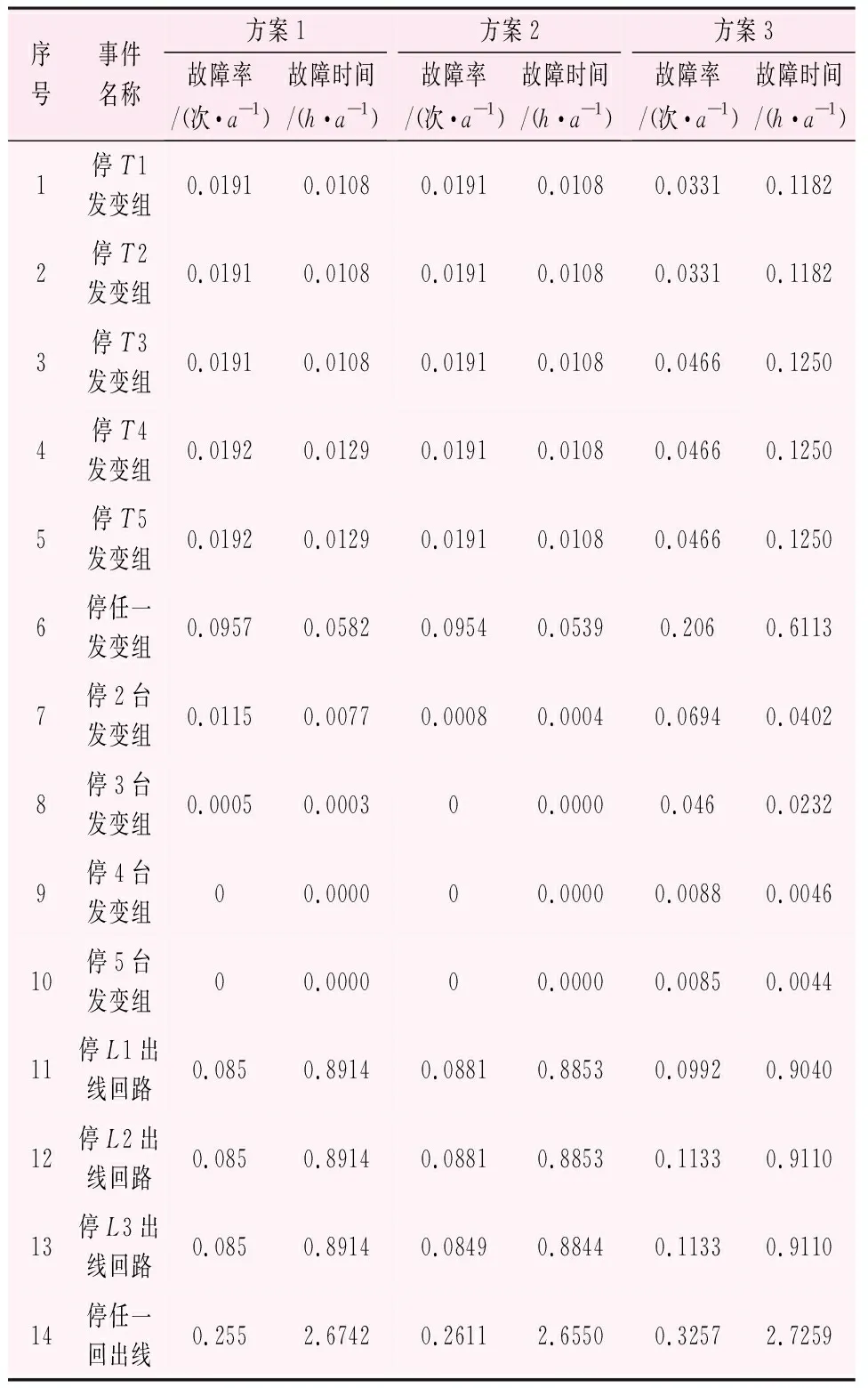
表3 决策事件

3 结 语

文章根据逻辑表格法在水电站、抽水蓄能电站可靠性分析中应用较广，但基本采用手工计算的现状，对AutoCAD进行二次开发，实现逻辑表格的程序计算，并对我国近些年发布的设备可靠性指标进行了收集与整理，可作为可靠性分析的设备基础数据。

文中收集的可靠性基础统计数据只到2017年，发电机断路器平均故障率和平均线路长度相关数据较少，在之后的工作中将对相关的数据做进一步的收集与整理。