基于四阶Newton-Cotes公式优化背景值的灰色自记忆模型研究及应用
张高锋,马 艳,程 龙,苟耀峰,孙小敏
(1.中国电建集团西北勘测设计研究院有限公司,西安 710065;2.西安市二次供水管理中心,西安 710016;3.西安市高新区农业农村和水务局,西安 710076)
0 前 言
水是生命之源、生产之要、生态之基,随着经济社会快速发展,地区用水需求呈现快速增长趋势,水资源供需矛盾日益凸显。科学合理的预测经济社会发展用水需求,是地区水资源规划的基础和前提,对于保障地区经济社会发展用水,合理确定供水工程规模具有重要意义。目前水资源规划主要采用定额法、趋势法等进行经济社会发展需水预测,但现有方法计算成果往往与实际存在较大偏差。为进一步提高规划设计中需水预测成果的准确性,急需探索新的预测理论与方法,为地区用水量预测提供科学依据。
始于20世纪80年代的灰色预测技术,以其对需水预测等研究对象存在的“小样本”“贫信息”有效处理,而受到国内外学者的广泛关注[1-2]。为了进一步提高模型精度和稳定性,2003年范习辉[3]率先将灰色预测模型与自忆性原理相结合,构建了具有记忆功能的灰色自记忆模型,随后灰色自记忆模型在径流预报[4]、凌汛水位预报[5]、降水量预测[6]、地下水位变化[7]、水电站入库径流预报[8]、城市用水量预测[9]等领域得到应用,取得一定成效,但模型精度仍有待提高。
众所周知,灰色自记忆模型的回溯阶和灰色系统动力核形式是影响灰色自记忆模型预测精度的2个重要因素,其中回溯阶选取可采用试算法确定,灰色系统动力核的形式则取决于灰色微分方程的发展系数a和灰作用量b,而a和b两个参数求解又依赖于灰色微分方程背景值的构造形式[9]。因此,构建更加科学合理的背景值成为提高灰色自记忆模型精度的关键。本文从影响灰色自记忆模型精度的动力核形式出发,通过对灰色微分方程的背景值进行优化,在此基础上构建基于背景值优化的灰色自记忆模型,并将其应用于地区需水预测中,以期为水资源规划中需水预测提供新的依据。
1 灰色自记忆模型
设有原始时间系列X(0)={x(0)(1),x(0)(2),…,x(0)(n)},将其按照下列累加生成新的数列:
X(1)={x(1)(1),x(1)(2),…,x(1)(n)}
(1)
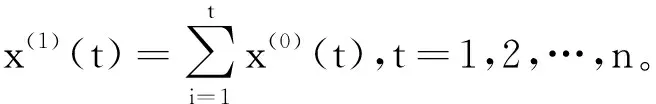
对于新数列建立一阶线性微分方程:
其中:a为发展系数,b为灰作用量,按照公式(3)计算。
(4)
计算出灰色微分方程参数a、b后,将公式(2)移项得到dX(1)(t)/dt=-aX(1)(t)+b,将此微分方程作为动力核,运用自忆性原理即可建立灰色自记忆模型:
式中: αi,θi为记忆系数,yi=1/2(xi+xi+1),f(x,i)为动力核,p为回溯阶。
若令

则公式(5)可写成如下的矩阵形式
X=YA+FW
(7)
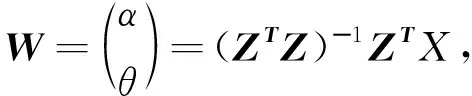
2 基于四阶Newton-Cotes公式优化背景值的灰色微分方程
从灰色自记忆模型的建模理论可知,灰色微分方程背景值的构造形式,对于灰色自记忆模型的精度具有重要影响,传统灰色微分方程背景值采用原始系列一阶累加值相邻数据均值进行计算,即采用梯形公式进行构造,而实际背景值为一条曲边梯形(如图1),图中阴影部分即为采用梯形公式构建背景值所产生的误差。为了进一步提高模型精度,应用四阶Newton-Cotes求积公式对灰色微分方程背景值进行优化。

图1 实际背景值与构造背景值对比
将区间[n-1,n]=[a,b]划分为n等分,则区间上任一等距节点xk=a+kh,k=0,1…,4,步长h=(b-a)/n,则曲边梯形面积z(1)(n)可近似按照下式计算:
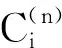
当n=4,b-a=1时,则得:
+7f(t4)]+Rn(f)
公式(10)即为四阶Newton-Cotes求积公式优化后的背景值公式,将公式(10)带入灰色微分方程即可得到四阶Newton-Cotes公式背景值优化后的灰色微分方程:
将公式(11)作为动力核,即可构建基于四阶Newton-Cotes公式优化背景值的灰色自记忆模型,并进行拟合及预测。
3 应用实例
城市需水既包含已知信息,又包含未知信息或未确定信息,属于灰色系统[9]。根据上述建模思路,选取北京市1995—2015年用水量作为建模样本,建立基于四阶Newton-Cotes求积公式优化背景值的灰色微分方程如下:
将公式(12)作为动力核,进一步建立基于四阶Newton-Cotes求积公式优化背景值的灰色自记忆模型。取回溯阶p=6,则模型记忆系数为:
α=[0.1600 -0.4112 0.5893 -0.9702 0.9352 -0.9179 1.6290]T
θ=[0.0756 0.0832 0.0623 0.1039 0.0370 0.1285 0.0032]T
(13)
求出记忆系数后,即可用所建模型对北京市2016—2020年用水量进行预测。模型拟合及预测结果见表1、图2。由于回溯阶取p=6,所以1995—2001年用水量无拟合值。

表1 基于四阶Newton-Cotes求积公式优化背景值的灰色自记忆模型拟合及预测值
从表1可知,基于四阶Newton-Cotes求积公式优化背景值的灰色自记忆模型拟合和预测效果较好,模型最大相对误差3.93%,平均相对误差-0.4%。采用后验差法[15]对所建模型精度进行评价,检验标准见表2,评价结果见表3。从检验结果可知,模型拟合部分后验差比值C=0.30,小概率误差P=1.00,模型精度好;模型预测部分后验差比值C偏大(C=0.62),小概率误差P减小(P=0.80),模型精度合格,这主要因为2019年实际用水量发生较大突变,出现了极值,加之预测部分样本较少,一旦某个预测值与实际值相差较大,都会极大的影响预测部分精度。但总体上来看,模型后验差比值C=0.4,小概率误差P=0.95,模型精度等级合格,能够满足实际应用要求。

图2 基于四阶Newton-Cotes求积公式优化背景值的灰色自记忆模型拟合及预测

表2 后验差检验标准

表3 模型拟合结果检验统计
4 结 论
本文针对现有需水预测方法计算成果往往与实际存在较大差距问题,从城市需水的灰色特性出发,通过对灰色微分方程的背景值进行优化,在此基础上构建基于背景值优化的灰色自记忆模型进行城市需水模拟和预测,得出结论如下:
(1) 需水预测属部分信息已知,部分信息未知的灰色系统,以往的灰色自记忆模型采用的灰色微分方程背景值按照原始系列一阶累加值相邻数据均值进行计算,而灰色微分方程实际背景值为一条曲边梯形,探讨灰色微分方程背景值优化方法,对于提高模型精度具有重要意义。
(2) 采用四阶Newton-Cotes求积公式对灰色微分方程背景值进行优化,并结合自记忆理论,构建了基于四阶Newton-Cotes求积公式优化背景值的灰色自记忆模型;通过在用水量预测值应用,表明模型精度总体较好,可作为水资源规划设计中需水预测的依据。
(3) 从模型拟合和预测部分精度看,拟合部分精度好,达到一级标准,预测部分受样本数较少以及2019年用水量发生突变等影响,精度有所降低,达到合格等级,这也表明对于极值预测效果,该模型精度有待进一步提高。

