倾斜角对片状样品太赫兹光谱的影响

杨 颀，秦凡凯，孟昭晖，杨义勤,陈 儒，李 超，詹洪磊，苗昕扬，赵 昆

(中国石油大学(北京) a.新能源与材料学院;b.中国石油和化工联合会油气太赫兹波谱与光电检测重点实验室，北京 102249)

太赫兹波通常指频率在0.1～10 THz之间的电磁波，其波段介于微波和红外之间，具有瞬态性、相干性、低能性等特点，在诸多领域已有广泛的应用. 在太赫兹光谱测试时，通常将块状、颗粒状、粉末状的样品制为片状，如岩石切片、农业种子压片、生物样品制片等[1-4]. 在实际制样中会在样品前后表面引入微小的倾斜角度，以致样品的实际形状为楔形，倾斜角对太赫兹波的传播和材料参量的计算产生影响. 由于太赫兹波在楔形样品表面和内部传播过程中的反射、折射及通过样品时光程的变化容易被忽略，因此探究楔形样本对太赫兹波传播过程的影响至关重要.

基于菲涅耳公式，建立了透射式太赫兹时域光谱的传递函数模型，并利用该模型提取出材料的光学参量，该方法广泛应用于对太赫兹吸收较弱的材料，但必须满足一定条件：样品前后表面必须平行且厚度均匀，待测样品表面是磁性各向同性的，太赫兹光束垂直入射样品[5-6]. 建立在太赫兹频率范围的全变差最小化模型[7]、材料色散模型[8]、双层结构模型[9]等，利用准直空间法[10]、单纯形法[11]等光学参量的优化算法，消除了厚度误差、Fabry-Perot震荡和信号噪声的影响，并同时计算未知均匀样品的厚度和复折射率，提取出更准确的材料参量. 现有的计算模型均需要保证样品前后表面平行、厚度均匀，而实际待测片状样品的厚度非均匀性很难完全消除，太赫兹波通过表面存在倾角的楔形样品时，太赫兹光束的方向和能量、太赫兹光谱波形及提取得到的光学参量的变化规律还有待研究.

本文建立了太赫兹波通过楔形样品的传递函数模型并做理论模拟，利用3D打印机制造不同倾斜角度的丙烯腈-丁二烯-苯乙烯共聚物(ABS)楔形样品用于实验分析，探究楔形样品对太赫兹时域光谱的影响，得到表面倾角对太赫兹波透过率振幅和相位的影响规律，修正楔形样品的光学参量计算模型. 在物理教学中，通过光学知识推导传递函数、光学参量的理论模型，利用3D打印技术制备所需参量的样品，结合实验验证，使复杂的太赫兹波在介质中传播过程易于理解.

1 原理分析

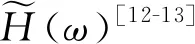
(1)

楔形样品和太赫兹光束通过楔形样品光路如图1所示. 由于样品表面倾斜，太赫兹辐射的入射角非零，从样品出射的太赫兹辐射将有复杂的光束几何关系，光束方向相对于光轴发生偏折，透过样品的太赫兹波的能量也将发生变化[15-17].

(a)楔形样品示意图

其中，γ，β，γ-β，θ分别为太赫兹脉冲通过样品的前表面和后表面的入射角和折射角，由Snell定律得到这些角度之间的关系为

sinγ=nsamsinβ,

sinθ=nsamsin (γ-β).

太赫兹波在样品中的传输距离l与样品中心厚度d和楔形样品表面倾角有关，

(3)

(4)

ρ(ω)和φ(ω)分别为复透过率的振幅和相位，经过推导可以得到楔形样品的参量，如折射率n(ω)、消光系数k(ω)和吸收系数α(ω).

当楔形样品的表面倾斜度增大时，太赫兹波传播的偏移量和通过样品的光程均增大. 由式(2)～(4)可知，在楔形样品中，折射率和消光系数、样品表面倾斜角度、太赫兹波在样品中的传输距离决定太赫兹时域波形的相位和主峰幅值. 实验中利用太赫兹光谱振幅和相位计算样品折射率、吸收率及消光系数时，如忽略样品表面倾斜角度引起的入射角和通过样品光程变化对计算结果造成的影响则会出现较大误差，由于误差对光学参量的影响呈以e为底的幂指数增长[18-21]，则楔形样品表面倾斜角度越大，计算值的误差越大，对实验结果造成的影响越大，因此需要对光学参量的计算方法进行修正.

一般光学参量计算模型计算折射率、消光系数和吸收系数时，只考虑光学参量与信号的振幅与相位关系，而楔形样品的测量结果受制于样品的倾角和通过样品的光程，利用式(3)～(4)解得包含倾斜角度相关项的光学参量的计算模型，使计算结果更准确.

2 理论模拟

图2 楔形样品透过率的振幅比随表面倾角变化

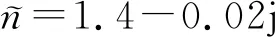
图3为楔形样品相位随表面倾角(0°～10°)变化. 由图3可以看出，相位φ(ω)随折射率n的增加而增加，在样品折射率确定时，相位随楔形样品表面倾斜角度的增加而呈指数增大，n=1.500，1.504，1.508时，相位随表面倾斜角度变化的幅度分别为0.081 8 rad，0.082 9 rad，0.084 0 rad，随折射率的增加楔形样品表面倾斜角度对相位的影响增大. 楔形样品表面倾斜角度的变化会影响太赫兹波在样品前后表面的入射角和出射角，使样品前后表面的折射和反射发生变化，同时改变了太赫兹波通过样品的光程，通过模拟数据可以看出楔形样品透过率的振幅和相位变化明显受到表面倾斜角度影响.

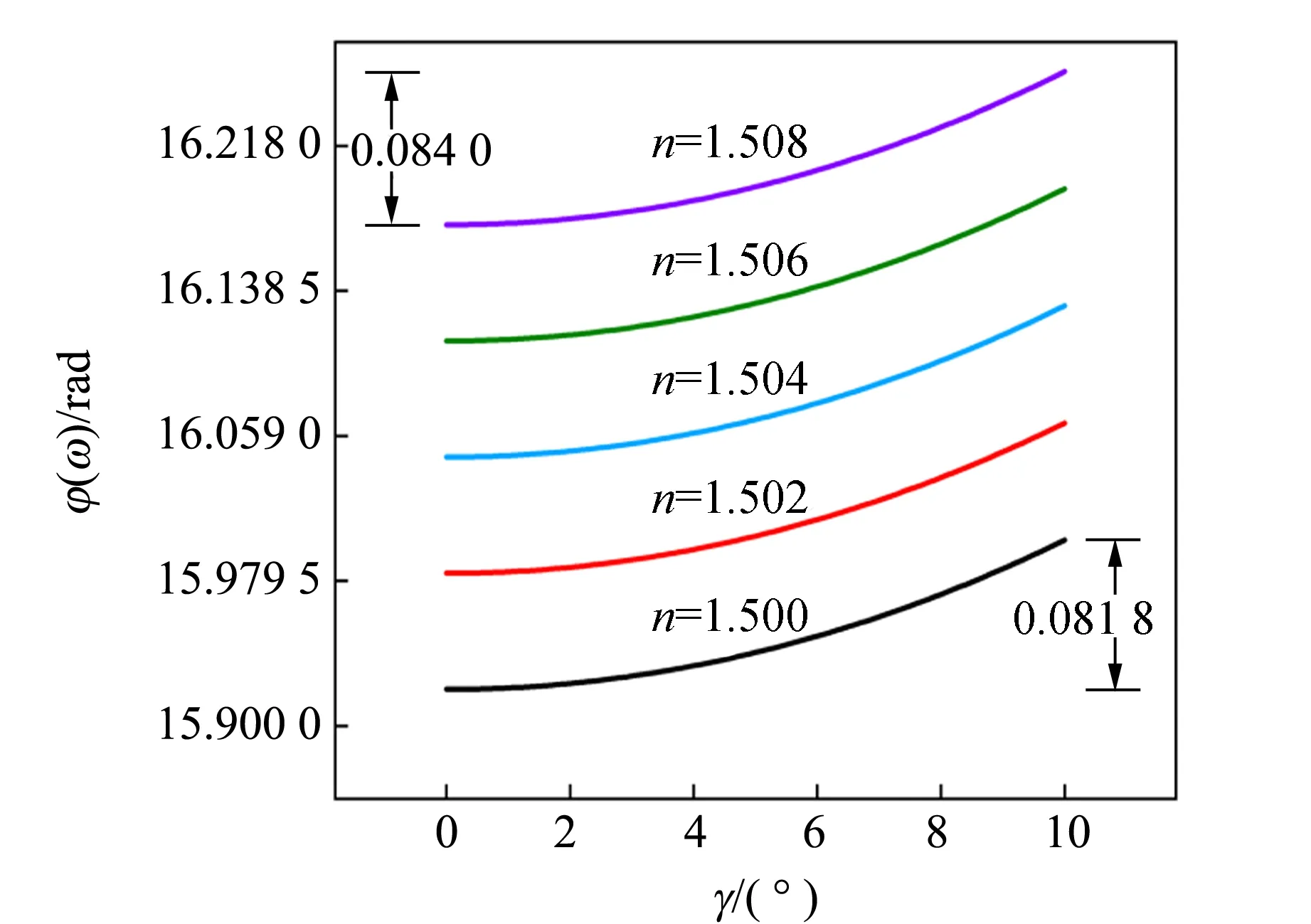
图3 楔形样品相位随表面倾角变化

在0.8 THz频率下，折射率n=1.5，消光系数k=0.02，中心厚度不同的楔形样品对太赫兹波透过率振幅比和相位的影响，如图4所示.

(a)

由图4可见：倾斜角度为0°时，随着样品中心厚度从1.900 mm增加到1.920 mm，振幅比由0.507 9降低到0.504 5，相位由15.920 6 rad增加到16.087 5 rad，随着样品中心厚度的增加，透过率振幅逐渐降低，而相位逐渐增加. 当样品厚度一定时，随楔形样品倾斜角度的增加振幅逐渐降低，且楔形样品厚度越小，表面倾斜角度对透过率振幅的影响越大；而相位随楔形样品倾斜角度的增加呈指数增长，样品厚度越大，倾斜角度对相位的影响越大.

通过理论模拟结果可以看出：当楔形样品中心厚度相差较大，而倾斜角度相差较小时，透过率振幅大小主要由厚度决定；当楔形样品中心厚度相差很小或相同时，样品表面倾斜角度会对透过率振幅造成很大影响. 不同折射率材料的楔形样品表面的倾角均会对太赫兹时域光谱幅值和相位产生影响，且影响程度不同.

3 实 验

楔形样品的透射式太赫兹光谱检测原理如图5所示，测试过程中温度为22～25 ℃，湿度为32%～36%，测试前先测试空气作为参考信号. 保证样品位置固定，太赫兹波穿过样品中心. 太赫兹源辐射的太赫兹波首先经过第1面反射镜，照射到样品中心位置，再经第2面反射镜后被探测器接收. 每个样品重复测量10次，保证每个样品测量时摆放位置、倾斜角朝向一致，得到样品太赫兹时域光谱数据，利用快速傅里叶变换获得与频率相关的振幅和相位信息，进一步计算得到样品的光学参量，例如吸收系数、消光系数及折射率.

图5 太赫兹光谱检测原理示意图

使用3D打印机制备2个表面倾角确定的均质丙烯腈-丁二烯-苯乙烯共聚物(ABS)楔形样品进行实验：楔形样品ABS1的表面倾斜角为8.8°，厚度为5.300 mm；楔形样品ABS2的表面倾斜角为2.2°，厚度为5.200 mm. 利用太赫兹光谱系统对2个不同倾角的ABS楔形样品进行测试，结果如图6所示.

(a)时域谱

从太赫兹时域光谱图中可知，利用太赫兹光谱系统对ABS1和ABS2楔形样品进行测试时，波形的峰值有明显的变化，ABS1的太赫兹时域谱峰值明显低于ABS2，延迟时间变化不明显. 对时域谱进行快速傅里叶变换得到太赫兹频域谱，在0.1～1.0 THz频率下通过ABS2的太赫兹信号强度大于ABS1，楔形样品表面倾斜角度越大，太赫兹信号强度越小，由于楔形样品表面倾斜角不同，使太赫兹波与样品表面入射角和出射角发生变化，在楔形样品表面太赫兹波的反射、折射不同，同时经过样品的光程发生变化，对太赫兹光谱透过率的振幅产生影响.

实验以及模拟ABS1和ABS2样品在0.4～1 THz下的相位谱和计算得到的各光学参量如图7所示.

1)从图7(a)中可以看出随着频率增加相位差线性增大，ABS2的相位差略高于ABS1，模拟数据和实验数据趋势相同，在频率为0.6 THz处模拟数值与实验数值吻合度最好，在0.6 THz处ABS1和ABS2的相位相差0.018 4 rad.

(a)相位谱

2)利用一般光学参量计算模型通过相位差计算得到样品的折射率，如图7(b)所示，实验测得ABS1楔形样品折射率略小于ABS2样品.

3)消光系数的计算受到振幅和相位的共同影响，在0.4～1.0 THz下ABS1和ABS2的消光系数有明显差别，表面倾斜角较大的ABS1样品的消光系数大于ABS2样品，在0.7 THz处ABS1和ABS2消光系数的实验计算值分别0.039 5和0.028 6，理论模拟值分别为0.038 1和0.028 0，实验值与理论值基本相符.

4)由图7(d)可以看出，吸收系数随频率的增加呈线性增加，ABS1的吸收系数计算值明显高于ABS2，在0.7 THz处ABS1和ABS2的吸收系数相差295.

通过对ABS1和ABS2的振幅、相位和光学参量的实验和模拟计算，可以看出模拟数据与实验数据基本吻合，随频率变化的趋势相符，说明建立的传递函数模型可以反映出太赫兹波通过楔形样品时的变化，同时可以看出楔形样品倾斜角度的变化在实验中会对太赫兹波透过率的振幅和相位产生影响，所以一般的光学参量计算模型并不适用于楔形样品，不同倾斜角度样品计算光学参量时会产生误差，需要在楔形样品光学参量计算模型中加入与样品表面倾斜角度有关项对计算模型进行修正.

4 结 论

对于片状材料的太赫兹时域光谱测试而言，上下表面的微小倾角会对测试结果造成较大影响. 通过理论和实验研究可知:不同折射率材料的楔形样品对太赫兹时域光谱影响程度不同，随样品倾斜角度的增加透过率的振幅和相位变化均呈指数增长;对于中心厚度相近的样本，倾斜角度对太赫兹波形有较大影响，计算得到的光学参量存在误差，应在计算时加入倾斜角度相关项进行修正，提高实验结果的准确性. 通过建立楔形样品的传递函数模型进行模拟计算，结合3D打印样品进行太赫兹时域光谱测试，相位及各光学参量的模拟与实验结果相符，得到楔形样品的太赫兹光谱响应特征.