基于改进蚁群算法的二维MUSIC多谱峰搜索研究

陈 宇，王 彪

(江苏科技大学，江苏镇江212003)

0 引 言

空间信号到达方向(Direction of Arrival, DOA)作为声呐阵列信号处理的一个重点，其作用在于确定搜索空间信号源的位置。Schmidt[1]在 1979年提出的基于特征分解的多重信号分类(Multiple Signal Classificaion, MUSIC)算法真正突破了瑞利限，实现了超分辨DOA估计，以MUSIC算法为代表的基于特征分解的子空间算法得到了研究者的认可，该类算法一般需要在算法所对应的空间谱函数上进行谱峰搜索，计算量巨大。如何进行快速有效的谱峰搜索一直是研究的热点，可将谱峰搜索算法分为两类：无策略搜索算法和策略搜索算法。无策略搜索方法是指这类算法遵循固定的搜索方法来进行谱峰搜索，代表算法为传统的均匀遍历法，该算法根据预设的精度要求来对解空间进行遍历搜索，计算量大，且计算量随着精度要求的提高而增大。策略搜索算法中，有一类算法是采用分步搜索的办法，这类算法的特点是先进行粗搜索，再对部分区域进行细搜素，如文献[2]提出的算法，该算法将噪声子空间进行分块，逐步收敛到谱峰附近，再进行细搜素，但是空间中的信号并不能保证服从某一分布，所以分块的依据有待商榷；如果分块不合理，会在无信号空间进行搜索从而造成计算资源的浪费。文献[3-4]提出设置一个门限，然后通过大步进搜索，寻找出高于门限的谱峰所在的一个大致范围，再在该范围内进行小步进搜索，寻找出准确的谱峰。但是文中也表示，门限设置的好坏直接影响了算法的成功率。与上述策略算法不同，群智能算法充分利用了空间谱函数的形状[5-6]，确定相应的搜索策略从而快速收敛到谱峰附近；同时，群智能算法并不需要对空间进行分块，这大大加强了算法的鲁棒性。如文献[7]提出的基于遗传算法的MUSIC谱峰搜索技术，文献[8]提出的基于鸡群优化算法的谱峰搜索，都取得了很好的效果，但是由于群智能算法属于全局优化算法，所以鲜有文章考虑空间中存在多个信号源的情况，也即多谱峰搜索问题。

在实际应用中，水下或者水面经常存在多个信号源，同时有些信号源相距很近，例如海战中的航母编队。在该实际背景下如何快速准确地估计出所有信号源的波达方向是本文的研究重点。蚁群算法作为群智能算法中的典型算法，已有非常完善的应用背景与数学理论依据，本文利用蚁群算法来进行DOA估计的研究，并且针对传统蚁群算法的一些缺陷，提出了更加适合多谱峰搜索的改进蚁群算法，并利用仿真实验，证明了本文算法的有效性。

1 二维MUSIC算法

1.1 接收信号模型[9]

1.2 MUSIC推导[9]

通过特征分解可以将阵列协方差矩阵R划分为信号子空间与噪声子空间两个空间，即：

2 蚁群算法改进

2.1 蚁群算法介绍[10]

蚂蚁在寻找食物时，会在其经过的路径上释放一种可以称之为“信息素”的物质，蚁群内的蚂蚁对“信息素”具有感知能力，它们会沿着“信息素”浓度较高的路径行走，而每只路过的蚂蚁都会在路上留下“信息素”，这就形成一种类似正反馈的机制，通过这种机制可以快速找到食物源。而蚁群算法正是利用了这种特性来进行全局优化。

2.2 蚁群算法的改进

2.2.1 聚类分析思想

蚁群算法为全局优化算法，在迭代过程中会不断收敛到最优解附近。但是DOA估计为多谱峰搜索问题(当存在多个信号源的情况下)，每个谱峰的幅值不一样，所以蚁群往往聚集到幅值最高的谱峰附近，从而使得其他谱峰处蚂蚁较少，影响了估计的精度，也容易造成估计失败。针对该问题，本文创新地将机器学习中的聚类思想与传统的蚁群算法相结合，将每个谱峰周围距离该谱峰最近的蚂蚁归为一类，通过这种方式，使得蚁群可以互不干扰地分开搜索不同的谱峰。该改进的步骤为：假设蚁群规模为，在蚁群迭代开始之前利用信源数K，根据信息素最大且距离较远的原则从蚁群中找出K个聚类质心点[9-11]{C1,C2,… ,CK}，然后根据误差平方和最小准则将所有的蚂蚁进行聚类。则在第t次迭代中，误差平方和函数为

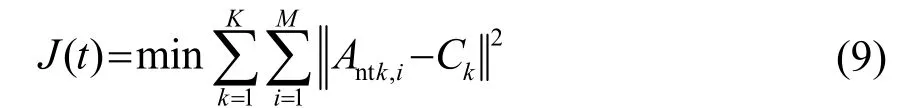
聚类完成后再进行算法的剩余部分，一次迭代完成之后再进行重新聚类，重新选取信息素更高的点作为质心点，所以本文提出的算法既是蚁群算法，同时也是完整的聚类算法。通过引入聚类思想，让属于不同族的蚂蚁去寻找不同的谱峰，从而避免了最高谱峰对蚁群算法性能的影响。

2.2.2 动态调整搜索范围

本文的蚁群算法采用了局部搜索和全局搜索两种搜索模式。在一次迭代中，蚂蚁采取哪一种搜索方式是由转移概率决定的；在第t次迭代中，第i个蚂蚁的转移概率公式为[7]

式中：T(…)表示信息素，Ci表示第i个蚂蚁所属族的质心点。则当该蚂蚁距离所在质心点较近也即Pi,t较小时，采用局部搜索，其搜索谱峰公式为

当该蚂蚁距离所在质心较远也即Pi,t较大时，采用全局搜索，其搜索公式为

式(11)～(12)中，co,t为第t次迭代后第i个蚂蚁的坐标，rnd为0～1之间的随机数，λt为第t次迭代的步长。dt-1为上次迭代后的搜索范围的上下边界差，转移概率Pi,t的大小往往用一个转移概率常数来衡量，本文取概率转移常数为0.05。设置上下边界可以防止蚂蚁跑出搜索范围，在传统的蚁群算法中，上下边界是固定不动的，比如需要搜索 -90°～90°范围的 DOA，则上界设置为 90°，下界设置为-90°。本文创新地随着蚁群算法的迭代调整搜索的边界，从而达到动态调整搜索范围的效果，调整的准则如下：

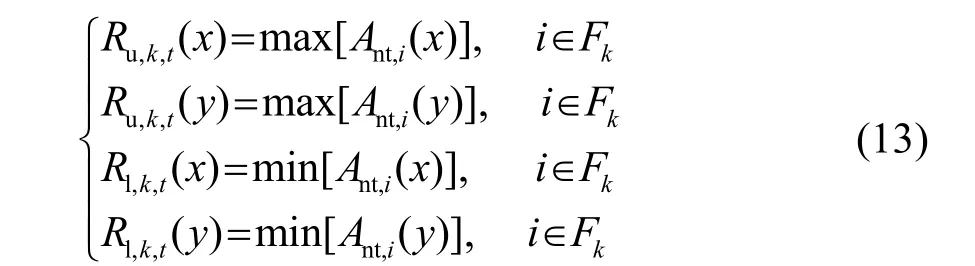
在同等仿真条件下，利用Matlab软件绘制出未使用和使用动态调整搜索范围的最终蚂蚁分布的投影图，其中图1(a)未采用动态调整搜索范围，可以看出蚁群可以分别收敛到三个谱峰附近，但是并不集中，这会造成虽然估计成功，但是收敛速度较慢、误差较大的问题，而图1(b)采用了动态调整搜索范围，可以看出蚁群不仅可以找到三个谱峰，而且收敛得非常紧密，通过这两张图的对比，可以看成该改进方法的有效性。

图1 采用与不采用动态搜索策略蚁群投影图Fig.1 Ant colony projection diagrams with and without dynamic search strategy

2.3 算法流程

结合了上述两个改进方法后，蚁群算法流程可以描述为：

(1) 设置最大迭代次数T，蚁群规模为A，目标误差为ET，信息素挥发常数Rau，转移概率常数p0，初始化迭代次数T为1，上边界为Ru,1，下边界为RL,1。

(2) 随机设置蚂蚁的初始位置，设置每只蚂蚁的初始信息素为其空间谱函数上对应的函数值。

(3) 运用聚类分析的思想在蚁群中找出K个质心点，将其余蚂蚁分成K个族。

(4) 计算每只蚂蚁的状态转移概率Pi,t。

(5) 更新每个族的上边界和下边界为Ru,k,t(x)，Ru,k,t(y)，Rl,k,t(x)，Rl,k,t(y)。

(6) 通过状态转移概率选择搜索模式。

(7) 对超出搜索范围的蚂蚁进行越界处理。

(8) 更新信息素，更新公式为

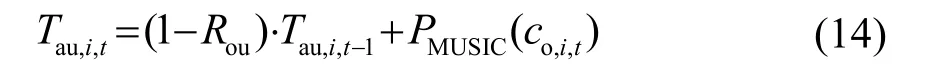
式中Tau,i,t为第i个蚂蚁在第t次迭代中的信息素，由两部分组成，加号前为经过挥发后残余的信息素，加号后为该次迭代中新留下的信息素。

(9) 得出本次迭代估计的谱峰值，即为各个族的质心点Ck,t，计算误差Et；如果误差Et小于目标误差ET，则结束；如果误差大于目标误差则转到步骤(3)，直到达到最大迭代次数或者误差小于目标误差。定义均方误差为

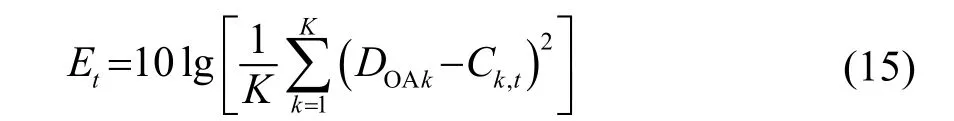
式中：DOAk表示与Ck,t相对应的实际波达方向。通过对误差取对数可以更好地绘制误差曲线图。

3 仿真与结果分析

3.1 实验设计

主要参数如下：阵元数为M=N=8，为 8×8的均匀面阵；快拍数为500；蚁群规模为400。

3.2 实验结果

设置信噪比为10 dB，迭代次数为100次，空间存在三个信号源，其波达方向分别为(10°, 15°)、(20°, 35°)和(30°, 55°)，绘制出空间谱函数与迭代前后蚁群分布图如图2所示。

图2(a)为迭代前的蚁群分布图，可以看出蚂蚁随机地分布在空间谱函数上，图2(b)经过50 次迭代后，所有的蚂蚁被分成了三个族，分别用红、黄、绿这三种颜色来区分不同的族，并且都收敛到了每个族对应的谱峰上，直观地说明了算法的有效性。实际DOA估计结果如表1所示。

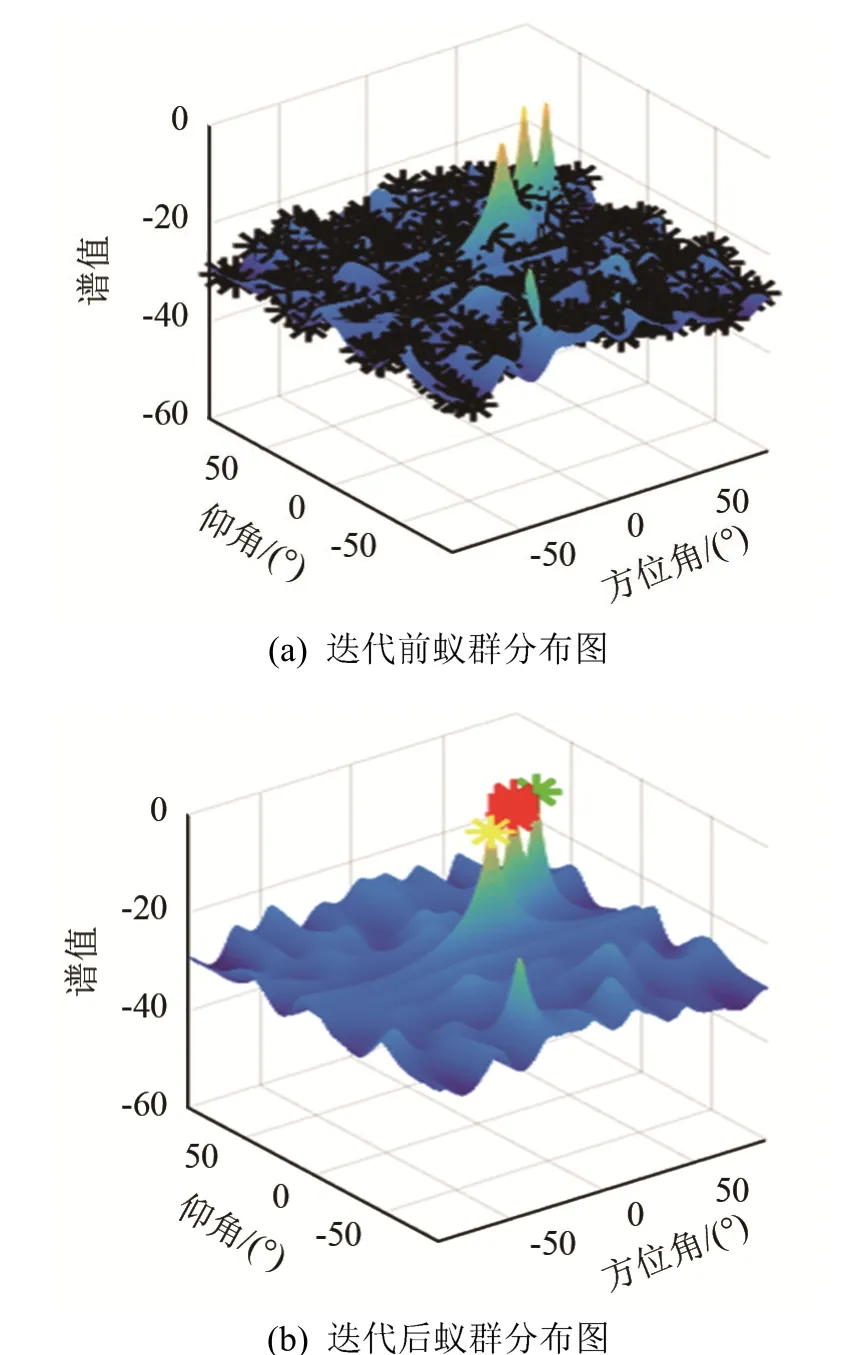
图2 迭代前后蚁群分布图Fig.2 Ant colony distribution maps before and after iteration

表1 DOA估计结果Table 1 DOA estimation results

设置信噪比为20 dB，迭代次数为100次，空间存在三个信号源，其波达方向为(10°, 15°)、(20°, 35°)和(30°, 55°)。本文提出的蚁群算法与传统蚁群算法的误差对比如图3所示，其中红色为传统的蚁群算法，蓝色为本文改进后的蚁群算法。从图3可以看出，迭代开始时，两种算法的误差大约都为25 dB，经过大约10次迭代后，本文算法的误差下降到0 dB，快于传统蚁群算法，经过大约40次迭代后，本文算法的误差下降到了大约-18 dB，体现出了该算法很高的估计精度。此后，由于受MUSIC算法分辨率限制，误差基本不再下降。而此时传统蚁群算法误差大约为6 dB，在接下来的迭代中，传统蚁群算法不能保持误差持续下降的趋势，最终误差为3 dB左右，精度明显低于本文提出的算法。这说明传统的蚁群算法并不能稳定且快速地进行多谱峰估计，而改进后的蚁群算法能够很好地完成任务。

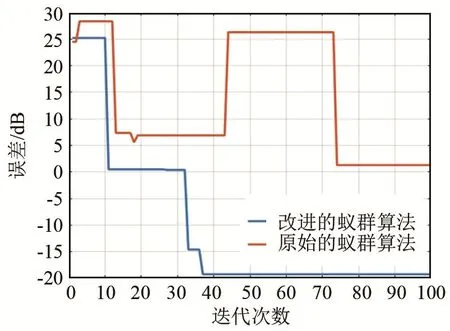
图3 算法改进前后误差对比图Fig.3 Comparison of DOA error before and after the algorithm being improved

为了探究信噪比与算法性能的关系，对本文在不同信噪比下多谱峰搜索进行了100次蒙特卡洛仿真，设置波达方向为3个，设置目标误差为5 dB，最大迭代数为 500。如果在最大迭代数之前达到目标误差，则认定该次实验成功，反之认为该次实验失败。统计结果如表2所示。

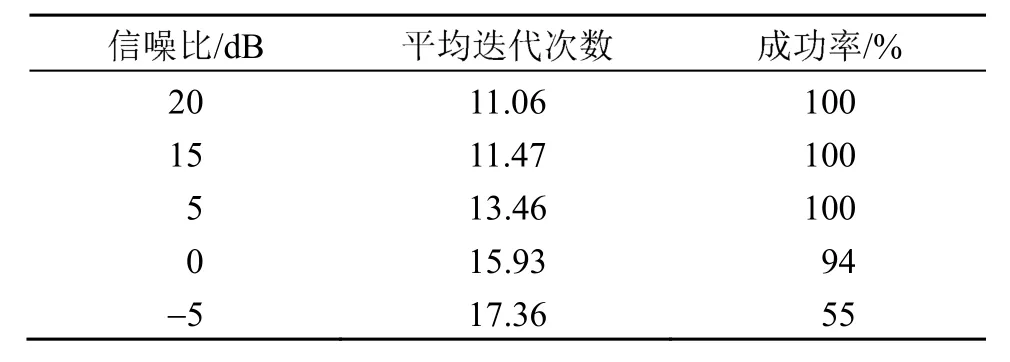
表2 不同信噪比下本文算法性能Table 2 Algorithm performance table under different SNRs

从表2可以看出，本文提出的算法在不同信噪比下迭代次数相差并不大，保证了不同信噪比下快速估计DOA的需求，且在高信噪比的情况下成功率均为100%，体现出本文算法具有较高的鲁棒性。但是在低信噪比情况下估计成功率较低，主要原因是低信噪比情况下二维MUSIC算法性能下降较快，有时甚至不会出现明显的谱峰。在这种情况下，本文的算法往往不能正确找到所有的波达方向，但可以找到空间谱函数中较为明显的谱峰所对应的波达方向。

为了探究在两个相近信号源情况下本文算法的性能，设置空间信号源的数量为 2，信噪比为20 dB，假设其波达方向分别为，则两信号源角度距离D定义为

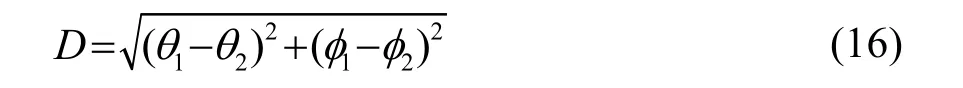
设置单次实验最大迭代次数为 100，进行 100次蒙特卡洛实验。谱峰靠近时搜索结果如图 4所示。从图4可以直观地看出，两个信号源非常靠近，其谱峰重叠部分非常大，仅可依稀分辨出两个峰尖。但是利用本文的算法依然可以准确地找到这两个信号源的波达方向。

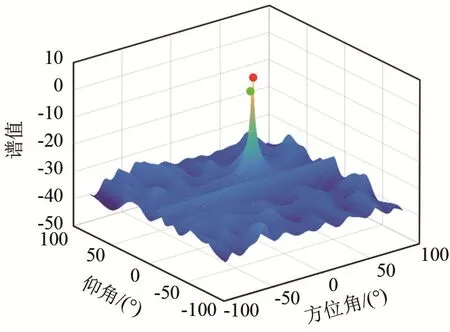
图4 谱峰靠近时搜索结果Fig.4 Search result graph when the peaks are close to each other

信号源靠近情况下，DOA估计的结果如表 3所示。

通过计算可以得出，表 3所示的估计误差为-1.3 dB，表明本文的算法可以正确估计出两个相近信号源的波达方向。

表3 信号源靠近情况下DOA估计结果Table 3 DOA estimation results when the signal sources are close

进一步探究多个空间信号源与信号源之间的角度距离对于算法性能的影响，设置空间信号源数量为2，改变两个信号源之间的角度距离，进行100次蒙特卡洛实验，实验结果统计如表4所示。

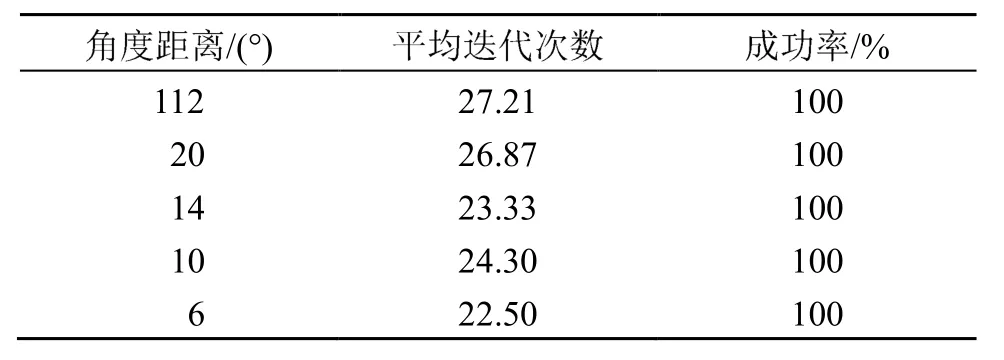
表4 不同角度距离下算法性能表Table 4 Algorithm performance table at different angle distances

从表4的结果可以看出，本文改进后的算法的估计成功率不受信号源之间角度距离的影响，可以应对不同的实际情况。

4 结 论

本文针对二维MUSIC算法多谱峰搜索存在的计算量大、容易失败等问题，提出了将蚁群算法与二维MUSIC相结合的解决办法，并针对多谱峰搜索的问题对传统蚁群算法进行了改进，包括与机器学习中的聚类分析相结合以及动态调整搜索范围。通过仿真可以看出，本文的改进蚁群算法可以很好地按照改进思路进行正确的聚类，并且可以在空间中存在多个信号源以及信号源比较靠近时正确地估计出他们的波达方向。与传统蚁群算法相比，改进后的蚁群算法可以完成多谱峰搜索且具有更高的估计精度，并且在较高信噪比环境下具有较高的鲁棒性。下一步的工作是改进该算法在低信噪比情况下的估计成功率。