预白化与小波变换联合的混响抑制方法研究

杨天霖，杜选民，周胜增

(上海船舶电子设备研究所，上海201108)

0 引 言

主动声呐在浅海环境工作时，受到各种各样的干扰，其中，以混响为主要干扰。非平稳、非高斯特性是混响的固有特征[1]，并且混响与主动声呐的发射信号具有强相关的特性。

在混响抑制方面，国内外学者开展了大量的研究。文献[2]利用自回归(Auto-Regressive, AR)模型，提出了对混响进行预白化处理的方法，此方法对混响没有约束条件，有一定的自适应功能。文献[3]在前者的研究基础上，利用混响的非高斯特性，基于混合高斯模型利用期望最大化(Expectation Maximization, EM)等算法对其进行参数估计，使混响背景高斯化。文献[4]利用水下声信道的多途特性，提出了模基匹配方法，相比常规处理获得了3 dB增益，这种方法的缺点在于需要提前获得水声环境的特性，声场需要准确计算。文献[5-6]利用分数阶傅里叶变换的聚焦性质抑制混响，但该方法只适用于线性调频(Linear Frequency Modulation,LFM)信号，且要求较高的信混比。文献[7]通过目标几何声散射成分与混响在Wigner-Ville时频面的形态特征表达式，利用图像形态学滤波去除Wigner-Ville中的混响，仿真表明在信混比为-5 dB的条件下可有效抑制混响。文献[8]提出了一种混合块归一化匹配滤波算法(Trimmed Mean Block Normalization of Matched Filter, TM-BNMF)，试验数据表明效果优于标准块归一化匹配滤波算法。文献[9]在混响背景下，利用预白化后的二分奇异值分解(Singular Value Decomposition, SVD)对匹配滤波器性能进行研究，提高了混响背景下匹配滤波性能[9]。

通过预白化能够有效提高匹配滤波器的检测性能[10]，而小波变换是在傅里叶(Fourier)分析之后发展起来的一种新的数学工具。在信号处理领域有着广泛的应用，具有多分辨特性(多尺度特性)，可以由粗到精地逐步观察信号。小波变换在水声中也有着广泛的应用。文献[11]给出了小波分析在水声非平稳信号中的应用，将小波变换用于舰船调制信息的检测。文献[12]提出了一种基于小波变换的阈值相关去噪算法。本文通过预白化联合小波尺度变换的算法，将混响和回波变换到不同的尺度空间，在不同的尺度下对数据进行处理，使得混响被有效抑制。仿真和试验数据处理结果验证了该方法的有效性。

1 AR模型预白化

匹配滤波器是在白噪声背景下的最佳检测器，预白化抗混响算法是将混响看成局部平稳的有色高斯随机过程，采用AR模型对混响进行建模，利用AR模型系数对原始数据进行“白化”处理[13]。无论x(n)是确定信号还是随机信号，对于线性系统，输入u(n)和输出x(n)之间的关系为

常用于估计AR参数的方法有自相关法、最大似然法、协方差法等，也有利用高阶累积量建立AR模型。AR参数估计中一种较为简易的方法是自相关法[14]，因其计算量小，易于工程实现，得到了广泛的应用。本文亦采用此算法进行混响预白化处理。该算法求解 Yule-Walker方程来估计模型的参数[14]，如式(3)所示：

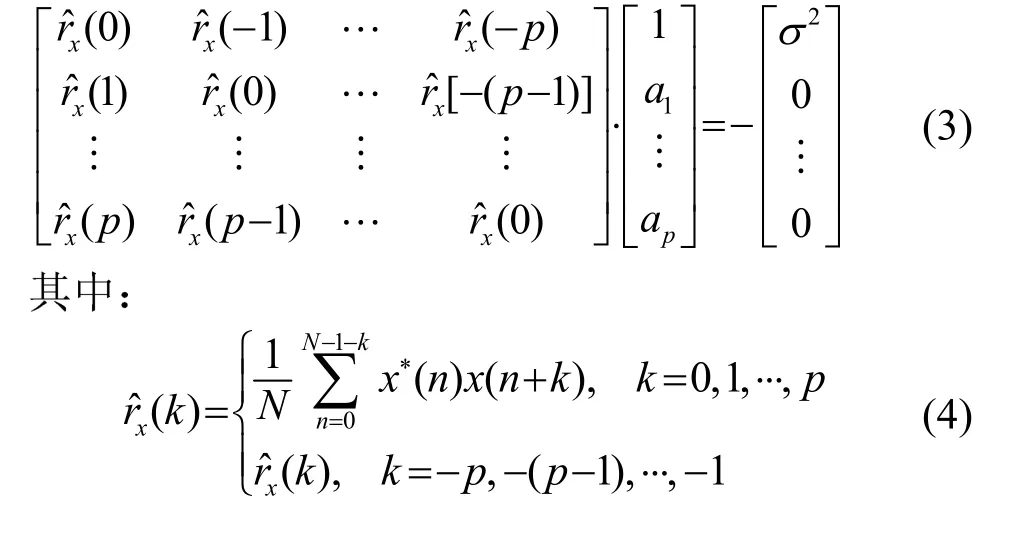
可以看出，一个p阶的AR模型由p+1个参数构成，即，只要估计出x(n)的p+1个自相关函数，然后通过高斯消元的方法即可直接求解方程。对于AR模型阶数的选择，通常由最终预测误差准则(Final Prediction Error Criteria, FPE)和信息论准则(Akaike Information Theoretic Criteria, AIC)结合工程实际经验共同得出。在本文中，AR模型阶数的选择，结合上述两个准则的参考，选定阶数为 20阶。若后文不特别说明，本文的仿真、海试数据处理对AR模型的阶数选择皆是20阶。

平稳随机信号的参数模型是AR模型的约束条件，因为混响的非平稳特性，在对混响预白化处理之前，通常假设混响信号局部平稳。一般混响的局部平稳性可用相邻两段混响功率谱的 Itakura距离来衡量[13]，其值大小反映了信号平稳与否。对于数据的功率谱分别为，非对称的Itakura距离[9]为

经过AR模型的预白化处理之后，混响背景具有类白噪声特性，更接近匹配滤波器作为最佳检测器的约束条件。但在信混比很低的背景下，因为混响完全淹没信号，白化后的输出信混比依然很低，这种检测结果也不甚理想。因此本文提出在预白化的基础上进一步利用小波变换的尺度特性进行联合处理，从而改善强混响背景下匹配滤波器的检测性能。

2 预白化与小波变换联合处理方法

本文利用小波变换的多尺度特性，通过选取尺度因子和平移因子，可以得到一个伸缩窗；通过合理选择小波，再经小波变换就可以表征信号的局部特征。因此在对混响预白化后进行小波变换，使得在强混响中匹配滤波器也能搜索到相关峰，提高混响抑制能力。

由连续小波变换的定义式可知，小波变换同傅里叶变换一样，都是一种积分变换，我们称WT，z(a,b)为小波变换系数，小波基具有尺度因子a和平移因子b两个参数。

离散小波变换是对小波基函数φa,b(t)中的a，b限定在一些离散点上取值。一般离散化方法是将尺度按幂级数进行离散化，即取，对b进行均匀离散取值，以覆盖整个时间轴[15]，这样小波基函数可以变为式(8)：

从小波变换的定义式可以看出，小波变换可以理解为把函数分解至位于不同的尺度分量上，这就是小波多尺度分解的原理。而小波变换的多尺度系数，有以下两点特性：

(1) 对于空间分布不均匀的函数，其小波系数只在少数部分有较大的值，而其他部分值很小。

(2) 对于均匀白噪声，它对所有小波系数的影响是一样的。

这样，利用小波的多尺度系数特性，能够有效提取干扰中的弱目标信号。

回波数据可以分为混响干扰和目标信号两种成分。通过预白化处理后，混响干扰被白化，而信号未被完全白化，通过小波变换的多尺度特性，能够有效提取其中的信号成分。小波变换将预白化后的数据分解到不同的尺度下，并进行阈值量化处理，从而在干扰中提取目标信号。

小波变换可利用的小波十分丰富，因为不同的小波对不同的信号形式、环境有不同的效果。对于小波的具体选取，没有一个标准，通常依据具体的问题进行具体分析选择。本文选用声信号处理中经常使用的Daubechies(db)小波进行分析[15]。

db小波具有较好的正则性，即该小波作为稀疏基所引入的光滑误差可以忽略，使得信号重构后比较光滑。Ndb表示的这个小波函数的消失矩，消失矩越大，它的支撑长度就越大，小波越光滑。同时频域的局部化能力就越强，频带的划分效果就越好，但会使时域紧支撑性减弱。考虑到主动声呐发射信号一般为宽带信号，对小目标探测的频率一般较高的特点，通过研究发现选取较高阶数的 db小波会更加有利。本文利用 db19小波进行分析，分解层级为7。

阈值量化处理包括软阈值和硬阈值。令M表示阈值，硬阈值信号y的形式为式(10)所示，软阈值信号y的形式为式(11)所示。硬阈值是最简单的处理方法，但硬阈值容易丢失信号中一部分有用的成分。而软阈值具有很好的数学特性。本文选取软阈值处理方法。

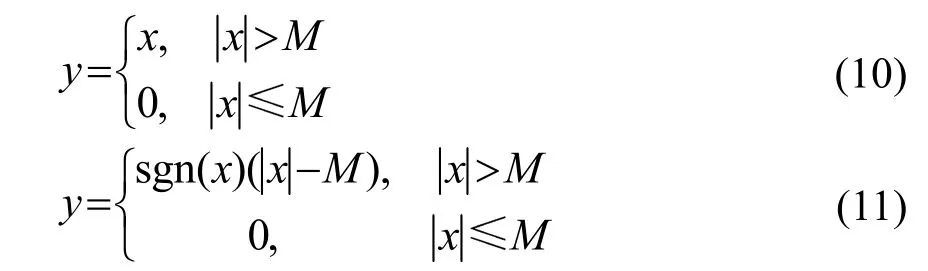
基于 Stein无偏似然估计原理的自适应阈值选择是一种软阈值估计[11]，选择准则相对保守，当信号的高频信息在干扰混响内时，这种准则能够保留信号的有用成分，最大限度保证信号的完整。本文选取该准则作为阈值的确定准则。

本文提出的算法的流程图如图1所示。其处理步骤如下：

图1 本文提出的算法处理框图Fig.1 Block diagram of the algorithm proposed in this paper

(1) 将接收数据分段并利用 AR预白化模型将数据预白化。

(2) 利用选取的db19小波进行7层分解，将预白化后的数据进行分解并提取系数。

(3) 小波尺度分解系数的阈值量化，依据上文所选准则计算得到一个阈值，并对各个分解尺度下的系数进行阈值量化处理。

(4) 小波重构。将尺度分解阈值处理后的数据进行重构。

(5) 对重构后的信号进行匹配滤波输出。

3 数据分析验证

3.1 仿真数据分析验证

本节通过仿真试验来验证本文所提方法的有效性。首先，基于 Middleton混响统计模型仿真混响[16]。仿真线性调频信号生成的混响，中心频率为7.5 kHz，带宽为5 kHz，脉宽为10 ms，周期为2 s。仿真混响的时域波形如图2所示，将混响进行分段(每段4 000 个点)，每段重叠50%，其Itakura距离[13]如图3所示。在随机某段的2 000点处加入LFM 信号作为目标回波，信混比为-8 dB。利用本文算法流程，分析对比常规匹配滤波、预白化匹配和本文处理方法，处理结果分别为图4、图5、图6所示。

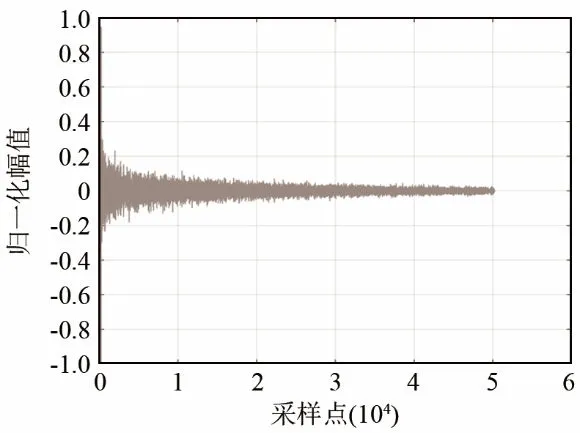
图2 基于Middleton模型的仿真混响Fig.2 Simulated reverberation based on Middleton model

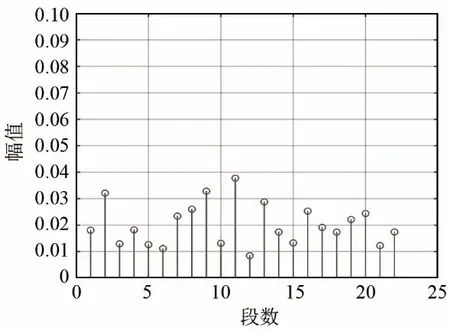
图3 仿真混响的Itakura距离Fig.3 Itakura distance of the simulated reverberation

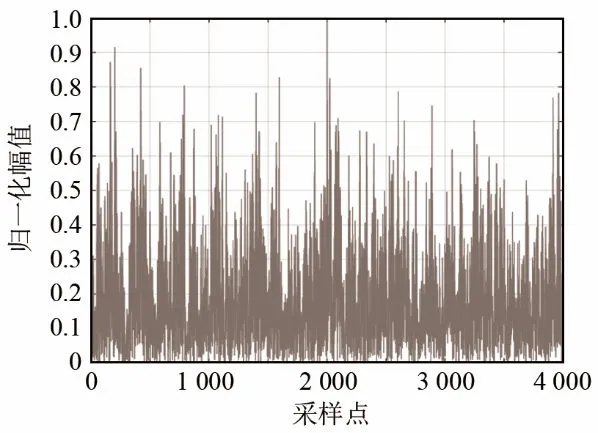
图4 常规匹配滤波器输出Fig.4 Output of the traditional matched filter

图5 预白化处理后的匹配滤波器输出Fig.5 Output of the matched filter after pre-whitening processing

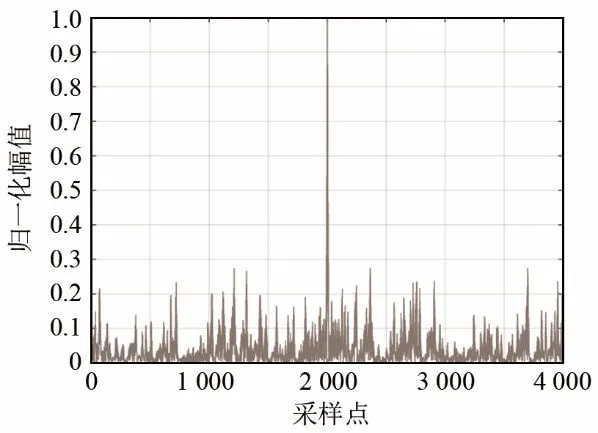
图6 本文算法处理结果Fig.6 Processing result of the proposed method in this paper

通过3种处理方法的结果比较可知，常规匹配滤波结果在信混比-8 dB 的情况下干扰已经十分严重；AR预白化匹配结果能够获得相关峰；从文本方法可以看到，相关峰出现的位置明显，并且通过本文方法的处理，混响干扰与前两种方法相比，有了明显的抑制效果。通过分析计算信混比可知，在-8 dB 信混比的情况下，本文方法较预白化处理的结果，有约4 dB的增益。

进一步量化比较，通过蒙特卡洛1 000次仿真实验，在虚警概率不大于0.1的条件下，得到性能比较结果如图7所示。

由图7中的比较结果可知，本文方法效果优于前两种方法。

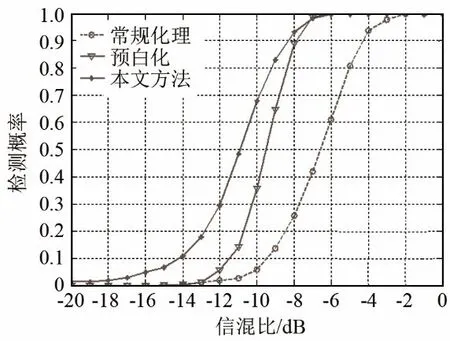
图7 3种信号检测方法的性能比较Fig.7 Performance comparison of three different signal detection methods

3.2 试验数据分析

3.2.1 单通道阵元数据分析

试验数据选用某次海试中某通道一周期阵元域混响数据，如图8所示。为了计算方便，将数据按6 000个点、重叠50%进行分段。图9为该通道某段混响数据。图 10为实验数据按上述分段后计算得到的Itakura距离。从图10中可以看到，当将数据按6 000个点、重叠50%分段时，其各段之间的Itakura距离都小于0.2，可认为在该段数据内混响满足局部平稳条件。

图8 单通道海试测得的混响数据Fig.8 The reverberation data measured in a single channel sea trial

图9 实测混响的某段数据Fig.9 A segment of the measured reverberation data

图10 混响数据分段后Itakura距离Fig.10 Itakura distances of the segmented reverberation data

将混响数据分段后，随机选取一段，加入与发射信号带宽相同的LFM信号，信号出现在2 000点，对试验的阵元域数据在信混比为-13 dB的情况下分别进行3种处理方式对比：直接匹配滤波、预白化后匹配滤波、经过预白化小波降噪后匹配滤波处理，结果如图11、图12、图13所示。

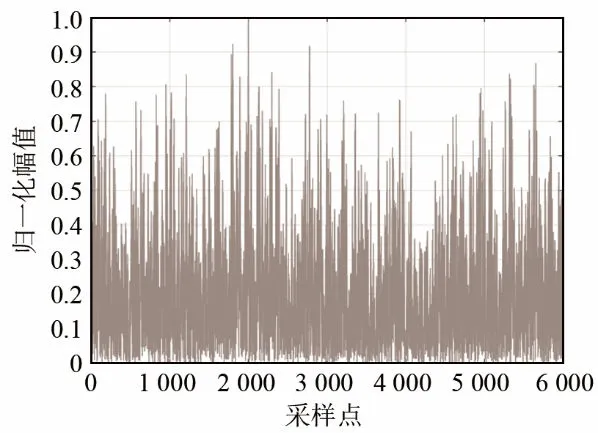
图11 实测混响背景下常规匹配滤波器输出Fig.11 Output of the traditional matched filter under the measured reverberation background

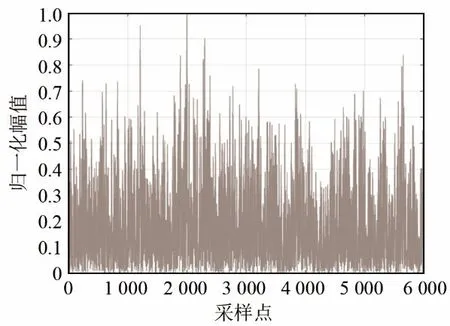
图12 实测混响背景下预白化处理后的匹配滤波器输出Fig.12 Output of the matched filter after pre-whitening processing under the measured reverberation background

图13 实测混响下本文方法处理后的匹配滤波器输出Fig.13 Output of the matched filter after using the proposed method in this paper under the measured reverberation background

通过3种处理结果的对比可以看出，在海试试验数据中，当信混比为-13 dB时，直接匹配滤波的处理峰值和AR预白化后匹配滤波的处理峰值已经淹没于附近的干扰之中了，几乎无法从中找到信号的相关峰；本文算法能够在采样点2 000 点附近有效提取峰值，通过分析计算信混比增益，性能较预白化方法提高约3 dB。

3.2.2 波束域海试数据分析

选取某次海试试验数据进行分析，对其先做常规波束形成。因为本文目的是验证算法的有效性，仅比较本文算法、预白化和常规处理之间的结果，不考虑后续处理。图14、图15、图16分别为常规匹配滤波、预白化后匹配滤波和本文算法处理后匹配滤波结果。预白化得到的结果已出现一定的偏差，因为海试数据中的目标为开式蛙人，而在蛙人行进过程中，产生大量的气泡，因此主动声呐探测的回波数据，通过匹配滤波处理之后，并没有呈现“一根线”的状态，而预白化处理出现的误差，是蛙人产生的气泡以及海域中散射体的混响对预白化算法产生了影响，从而产生了一定的偏差。而本文算法通过小波的尺度分解等处理，避免了这个偏差的产生。

图14 对实际目标检测的常规匹配滤波器输出Fig.14 Output of the traditional matched filter for real target detection

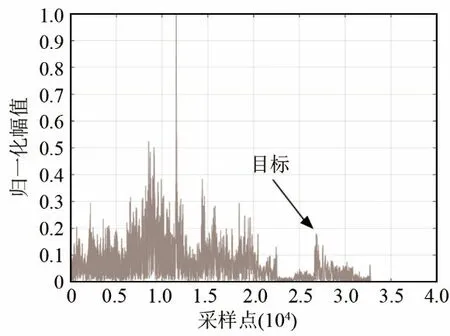
图15 对实际目标检测的预白化处理后的匹配滤波器输出Fig.15 Output of the matched filter after pre-whitening processing for real target detection

图16 对实际目标检测的本文方法处理后的匹配滤波器输出Fig.16 Output of the matched filter after using the proposed method in this paper for real target detection

本文算法相比其他两种算法能够有效提高匹配滤波器对目标的检测能力，但本文算法同时也会增强前面部分的干扰，其原因在于海试环境中存在的固定干扰的回波也被算法增强，后续可通过多帧联合处理的方法进行抑制。

4 结 论

针对混响背景下匹配滤波器性能下降的问题，本文提出了预白化与小波变换联合处理的方法，通过选取合适的小波，对小波变换后得到的尺度空间进行阈值化处理，算法的灵活度高，能够有效地改善强混响背景下匹配滤波的检测性能。仿真和试验数据处理结果验证了算法的有效性，本文算法较预白化算法，能提高约3 dB的增益。本文算法为主动声呐混响抑制提供一个有效的途径，有一定的工程实用价值。

下一步工作将结合实际海试数据中出现的现象进行深入研究，验证该方法的普遍适用性。由于方法的约束条件为混响相邻之间局部平稳，对非平稳的情况有待进一步研究分析。