基于强度折减法的河道边坡稳定性研究

王腾飞，常 赜

(珠江水利委员会珠江水利科学研究院，广州 510611)

0 前 言

河道边坡的稳定和安全一直都是岩土边坡研究的重点，如何定量的描述河道边坡当前的稳定程度是重中之重，传统的做法是通过开展野外观察测量河道边坡的滑动量和河流水位来评判的，但这种做法工作量太大，效率较低，对人员数量需求较多，采样精度容易受到环境因素的不利影响。鉴于此，专家学者们提出了能满足一定精度要求的强度折减法来计算边坡稳定，文章也是基于该理论来开展对河道边坡稳定性的定量化研究，将通过各关键因素对稳定系数的影响来进行具体分析。

1 强度折减法基本原理

河道边坡的稳定系数取自强度折减法下的等效换算结果，计算有限元模型时，每一次迭代步都对河道边坡填充体的黏聚力C和材料内摩擦角φ等进行比例折减，同时判断边坡的稳定状态，当河道边坡出现滑动失稳时，也就是河道边坡填充体的应力无法与其塑性应变匹配时，填充体内部就形成了弧形连续滑动面，初始黏聚力C0与此状态下的黏聚力Cn的比值就是河道边坡的稳定系数。文章判断河道边坡滑动失稳的标准是：边坡填充体形成了贯通性塑性区(塑性应变最大且贯通边坡的区域)。

(1)

(2)

式中：C为填充体的黏聚力；Ci由上一步迭代计算得到；φ为填充体的内摩擦角；φi也由上一步迭代得到；i为等比例折减的次数；F为折减系数。若河道边坡经历了n次迭代后发生滑动失稳，则此时的折减系数Fn就是河道边坡的稳定系数，即：

(3)

式中：σ为填充体的法向应力；C0和φ为材料初始状态的参数。

2 河道概况

郁江是珠江流域西江水系最大支流，位于广西壮族自治区南部，流域总面积89357km2。北源右江为正源，发源于云南省广南县境内的杨梅山；南源左江源于越南境内。拟分析河道边坡距离上游西津水利枢纽81km，距离下游贵港航运枢纽23 km。左右岸均为水田、旱地，以10a一遇洪水位线(49.95m)作为河道管理范围控制线，河宽10a一遇时约为364.67m，河床高程一般在20m-45m，平均坡降为0.1‰。

3 建立河道边坡有限元模型

以商用有限元软件ABAQ US为平台建立河道边坡平面模型，如图1所示，模型采用八节点四边形单元，并细化了边坡潜在滑动区的单元尺寸。边坡坡度分别设置为15°和30°，坡度15°的河道边坡常水位1.3m，地下水位1.4m，单元数量为388个。坡度30°的河道边坡常水位0.5m，地下水位0.6m，单元数量为412个。填充体所用材料的干密度为1.26g/cm3，静杨氏弹性模量为26MPa，泊松比为0.25，黏聚力为9kPa，内摩擦角为16.7°，孔隙比设置为0.71，渗透系数考虑3.22×10-7m/s[1]。

(a)15°坡度

模型荷载考虑水和填充体的自重。对模型左右断面及底部设置固定约束。渗流边界条件是自由水面以上的边坡为自由渗流，左断面及其他自由水面以下的边坡受河流自由水头作用，右断面受地下水位影响。初始条件是填充体内的孔隙水压力随埋深的增加而线性增加。

4 算例验证

为验证强度折减法对本研究课题的可行性，文章在ABAQUS和GEO-studio软件中建立了同样尺寸和边界条件的河道边坡平面模型，前者基于强度折减法来计算和判断河道边坡的稳定性，后者则利用极限平衡法。如图2、图3所示，对坡度15°且水位降落期为48h的河道边坡滑动失稳的计算结果表明：水位降落过程中，潜在滑动区的地下水渗流场围绕其顺时针流动，渗流流速均朝着下坡向，且靠近坡面渗流场的流速基本与坡面平行，两个软件计算的地下水最大渗流速率差异较小；从滑动面的分布情况可以看出，ABAQUS计算滑坡带的深度较GEO-studio的浅，但两个滑动带的形状和位置基本一致。由此可认为强度折减法适用于研究本课题。

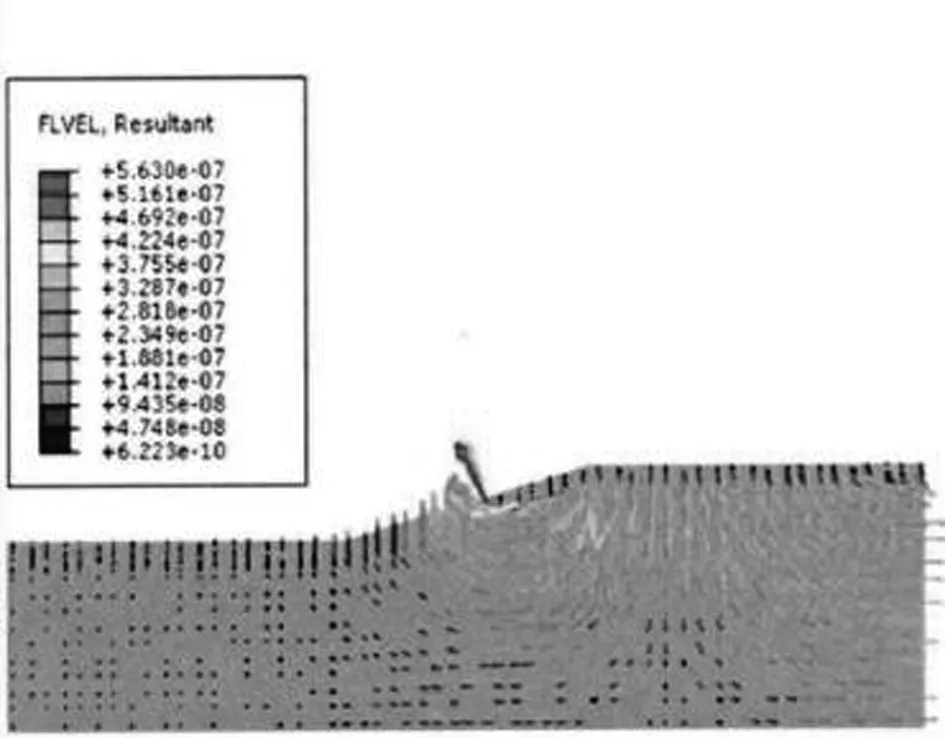
(a)ABAQUS的计算结果

5 河道边坡的稳定性分析

有研究表明水位降落会影响河道边坡的稳定和安全，文章设置了15°和30°坡度以及24h、48h、72h三个水位降落期来开展河道边坡稳定性的数值模拟。

5.1 15°河道边坡稳定性分析

15°河道边坡渗流场，如图4所示。

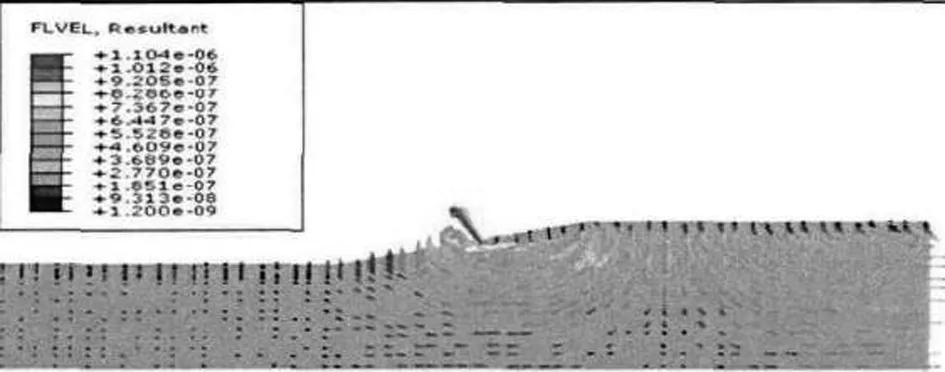
(a)24h水位降落期

从图4可以看出，24h、48h和72h水位降落期下的边坡地下水渗流场形状较相似，最大渗流速率随水位降落期的延长而降低，不同水位降落期对应的最大渗流速率依次为1.1-6m/s、5.6-7m/s、3.8-7m/s，造成这一结果的原因主要是：较长的水位降落期会让边坡填充体的孔隙水水位降落得更缓慢，孔隙水对地下水的渗流有阻碍作用，进而减缓了渗流速率。

图5是河道边坡滑动失稳时的塑性区分布图，在不同水位降落期影响下，边坡塑性区的位置、面积存在一定差异性，边坡塑性区面积随水位降落期的延长而缩减，其位置也沿竖直方向向上转移，贯通性塑性区中心到坡面的距离也越来越小。这一结果的主要影响因素是原滑坡体的负孔隙水压力随水位降落期的延长而增高，边坡的极限承载力逐渐恢复。由河道边坡填充体形成贯通性塑性区的判断标准可求得15°河道边坡在水位降落期24h、48h、72h下的稳定系数依次为3.32、3.34、3.35。

(a)24h水位降落期

5.2 30°河道边坡稳定性分析

30°河道边坡渗流场分布如图6所示，可以看出水位降落期24h、48h、72h影响下的河道边坡渗流场的形状、位置均与图4的结果相似，但由于本工况的坡度增加了一倍，这就使得填充体的孔隙水水位降落速率较15°坡度的模拟结果更快，很大程度上削弱了孔隙水对边坡渗流的阻碍作用，导致30°河道边坡的最大渗流速率达到4.8-6m/s、2.9-6m/s、1.9-6m/s，远>15°河道边坡的结果。

(a)24h水位降落期

图7是河道边坡发生滑动失稳时的塑性区分布图，与图5的结果对比后发现，图7的河道边坡塑性区的应力水平有所下降，塑性区位置也更靠近坡面，其深度较浅，相同水位降落期下的贯通性塑性区中心到坡面的距离稍大，其稳定系数分别降至2.31、2.33、2.34，衰减幅度约为30%。

(a)24h水位降落期

6 结 论

文章以强度折减法为理论依据，在有限元软件ABAQUS的支撑下展开了河道边坡稳定性的仿真研究，得到以下结论：

1)对比ABAQUS和GEO-studio计算的河道边坡渗流场的结果，可以发现二者无明显差别，其渗流场形状、位置较相似，最大渗流速率基本相等，滑动带的形状、深度相似，所以强度折减法对本研究课题的可行性得到了验证。

2)同一坡度下，水位降落期是影响河道边坡稳定的关键因素，具体表现为水位降落期越长，孔隙水的退散速率越小，边坡极限承载力的恢复程度越高，其稳定系数就越大。

3)水位降落期相同时，河道边坡的坡度越陡，孔隙水的退散速率越大，边坡极限承载力的恢复程度越低，稳定系数越小。

4)对于具体河道边坡案例，可以在强度折减法的基础上，通过模型精细化、材料分区、考虑植被覆盖等措施来增加数值模拟的可靠性。