气压对压力容器前壁超高速撞击损伤的影响*

迟润强，段永攀，庞宝君，才 源

（1. 哈尔滨工业大学空间碎片高速撞击研究中心，黑龙江 哈尔滨 150001；2. 黑龙江科技大学理学院，黑龙江 哈尔滨 150022）

航天器上的充气压力容器为储能部件，一旦遭受空间碎片撞击，可能发生泄漏或爆炸，造成航天器部分功能丧失甚至整个系统失效[1]。压力容器在超高速撞击下的损伤失效行为非常复杂，前壁损伤是其中一类重要模式，主要包括前壁穿孔和穿孔处的裂纹失稳破坏。高压气体在容器壁上产生的预应力以及气体介质的存在，对前壁失效可能产生不同的影响机制。

在一些压力容器超高速撞击实验中，未将压力容器的前壁穿孔特性作为重点研究对象，仅列出并简单描述了零散工况下的前壁穿孔尺寸[1-2]。有些研究开展了有针对性的前壁穿孔特性分析，基于实验和数值模拟手段，或多或少讨论了前壁穿孔尺寸随弹丸直径、前壁厚度、撞击速度等参数变化的规律，而对气体压强的影响考虑较少[3-4]。庞宝君等[5]指出，气体压强对前壁穿孔影响较小，但在其数值模型中，气体压强是通过应力边界条件施加在容器内壁上，忽略了高压气体的建模。

针对前壁穿孔处的裂纹失稳破坏问题，Igor 等[6]认为，弹丸穿透前壁之后产生的碎片云压缩容器内的气体，形成气体冲击波并在容器后壁反射，再通过气体介质传到容器前壁，在前壁产生一个瞬时压力加载，导致前壁穿孔处发生裂纹失稳破坏，并且在文章中定性描述了冲击波反射后到达前壁的传播过程。然而，多数学者仅以碎片云头部气体冲击波特性为研究对象，如Schäfer[1]、Smirnov 等[7]探讨了碎片云与气体的相互作用，对碎片云头部气体冲击波的运动特性进行了分析，而对反射冲击波的运动特性及其对前壁裂纹失稳破坏影响的研究较少。

本文中，以球形铝合金充气压力容器超高速撞击前壁损伤为研究对象，开展实验与数值模拟计算，分析内充气体压强对容器前壁穿孔形貌、穿孔尺寸的影响规律与影响机理，探讨碎片云压缩内充气体形成的冲击波在容器内的传播行为及其与前壁裂纹失稳破坏的关系，分析不同撞击条件下气体冲击波对容器前壁穿孔边缘最大环向应力的影响。

1 实验与数值模拟

1.1 实验

在二级轻气炮上开展了压力容器超高速撞击实验。实验布置如图1 所示，球形压力容器通过靶架固定在真空靶舱中，由靶舱外气瓶经后部充气接口充入压强为p0的氮气，弹丸经二级轻气炮发射后，超高速撞击压力容器前壁，在靶舱侧面布置高速摄影机，测量弹丸撞击速度。真空靶舱内的气压低于200 Pa。实验所用压力容器如图2 所示，所用材料为6061-T6 铝合金，外径为250 mm，容器壁厚度 δ 名义值为2.5 mm，因加工误差并非完全相同。弹丸为2017-T4 铝合金球，直径D 为6.35 mm，撞击速度v0名义值为3.55 km/s，实际略有差别。有效实验共4 次，具体实验参数如表1 所示。

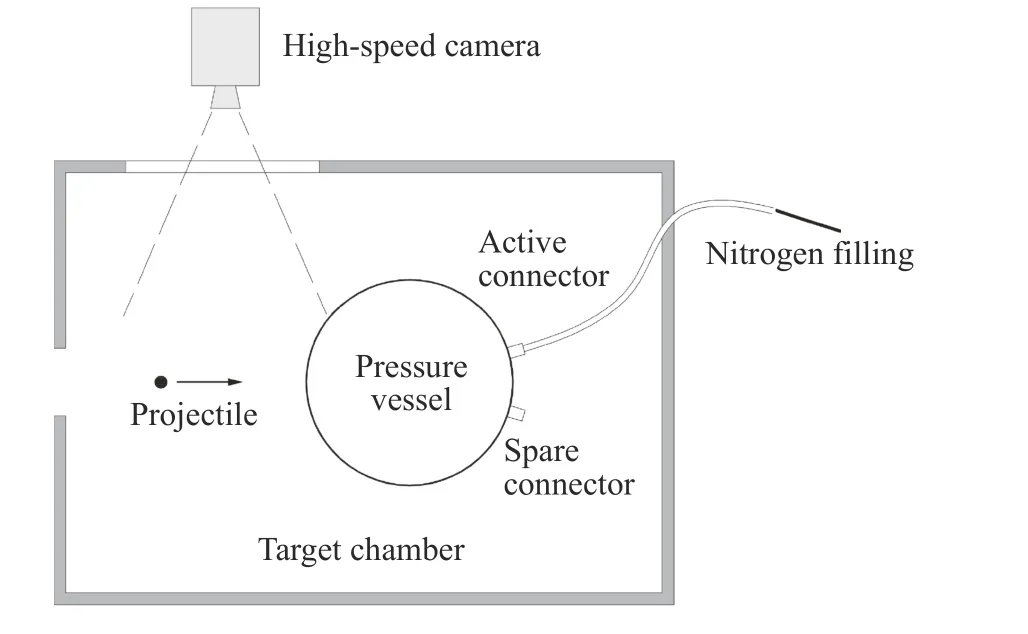
图1 实验布置示意图Fig. 1 Schematic diagram of experimental setup

图2 球形压力容器Fig. 2 Spherical pressure vessel

1.2 数值模拟

采用非线性动力学分析软件AUTODYN 建立2D 轴对称模型，模型包括3 部分：弹丸、压力容器壁和内充气体，撞击区域局部模型如图3 所示。容器壁与弹丸采用Lagrange 有限元方法建模，采取删除畸变单元的方式应对材料大变形和破碎问题。为了平衡计算精度与效率，在容器壁模型前壁弹着点附近一定区域内设置网格加密区，四边形单元尺寸为0.05 mm×0.05 mm，其余区域单元尺寸沿环向按比例放大。弹丸模型中的四边形单元尺寸为0.05 mm×0.05 mm。气体采用SPH 方法建模，应对气体大范围流动问题。容器壁和弹丸材料模型均采用Shock 状态方程、Johnson-Cook 强度模型和最大拉应力失效模型，材料参数引自文献[8]。内充气体采用AUTODYN材料模型库[9]中氮气的理想气体状态方程进行描述。除以上通用参数设置，根据数值模拟目的不同，将充气压力容器模型分为A、B 两类。

压力容器模型A 如图4 所示，包括容器壁和全部气体，能够真实反映压力容器中气体与容器壁的相互作用。在显式动力学软件AUTODYN中，通过设置初始气体压强及静态阻尼系数，模拟容器壁与气体之间的准静态加载，实现二者静力平衡，如图5 所示。将此时的压力容器模型作为后续弹丸撞击的对象。

压力容器模型B 如图6 所示，包括容器壁和局部气体，为等效模型。预先进行的数值模拟结果显示，在弹丸穿过后较短时间内，容器前壁穿孔便完全形成，远早于气体冲击波自后壁反射回前壁的时间及气体大规模泄漏的时间。因此，仅模拟前壁穿孔特性时，不需要压力容器模型A 这种全模型，为减小计算量，本文中建立了简化的等效压力容器模型B。该模型中，压力容器前壁具有区别于真空中薄板的两种典型特征：（1）容器壁承受气体压力，处于弹性膨胀状态；（2）容器壁内侧存在具有一定密度的气体介质。

对于典型特征（1），在容器壁模型内侧施加等同于气体压强p0的应力边界条件，如图6所示。利用与压力容器模型A 相同的准静态加载方式，使容器壁与应力边界条件达到静力平衡。结果表明，在相同气体内压作用下，压力容器模型B 中的最大主应力稍高于模型A，如图5 所示，主要原因为模型A 设置的是气体初始压强，待静力平衡后容器膨胀，作用在容器内壁上的压强略小于初始压强。因两种模型不同时使用，本文中忽略二者差别。需要说明的是，应用此方法计算弹丸穿孔直径时，待穿孔稳定形成以后，需删除应力边界条件，并继续计算至容器壁内无薄膜应力，以便符合真实气体泄漏后的情形。

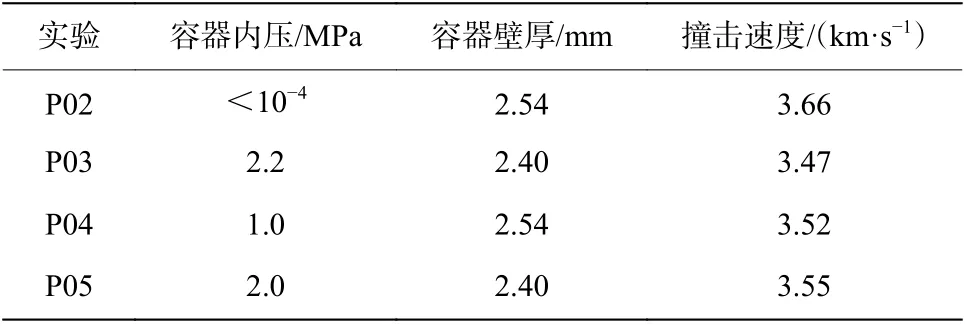
表1 实验参数Table 1 Experimental parameters

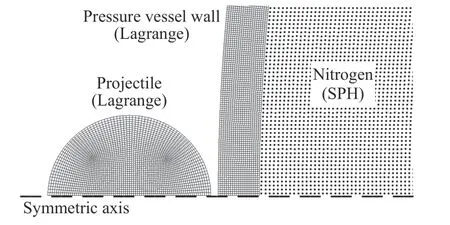
图3 二维轴对称模型局部Fig. 3 Local domain of two-dimensional axisymmetric numerical model

图4 压力容器模型AFig. 4 Numerical model A of pressure vessel

图5 球形压力容器壁中最大主应力时程曲线Fig. 5 Evolution of maximum principle stress on the spherical vessel wall

对于典型特征（2），在容器前壁内侧添加如图6 所示的局部气体模型，二者相互接触。局部气体模型为扇形，处于以模型对称轴为起始位置绕球壳中心顺时针旋转12.5°的区域内，外径与容器壁内径相同，内径为容器半径的1/2。通过设置气体材料模型中的压强修正值，使其具有与实际高压气体相同的密度而无内压。

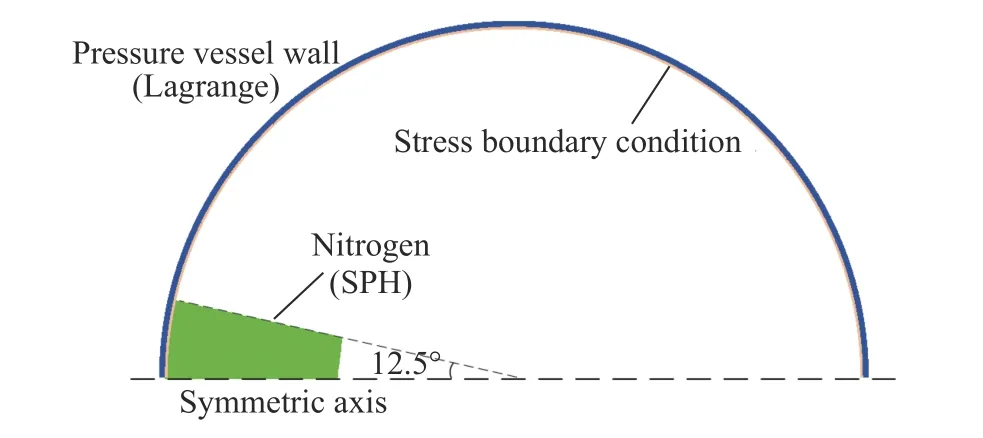
图6 压力容器模型BFig. 6 Numerical model B of pressure vessel

2 数值模型的实验验证

超高速撞击实验后，对压力容器进行观测，容器前壁的损伤形貌如图7 所示。由图7 可以看出，压力容器前壁损伤均为圆形穿孔，与超高速撞击薄平板形成的穿孔形貌相似。穿孔直径dh的实验与数值模拟结果如图8 所示。

图7 容器前壁穿孔外侧正视图Fig. 7 Photographs of holes shown from the impacted side of the front vessel wall

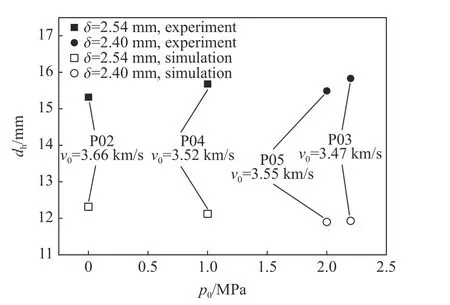
图8 容器前壁穿孔直径实验与数值模拟结果Fig. 8 Experimental and numerical hole diameters

由图8 可以看出，当容器壁厚 δ =2.54 mm 时，相较于实验P02，实验P04 具有较高的内压、较低的撞击速度和较大的前壁穿孔直径；当 δ=2.40 mm 时，实验P03 和P05 的撞击参数和前壁穿孔直径也观察到相同的现象。在相同容器壁厚度条件下，前壁穿孔直径受撞击速度和内充气体共同影响，根据典型的薄板穿孔特性，穿孔直径与撞击速度成正比。因此，上述现象初步说明，增加内压能够在一定程度上增大压力容器前壁穿孔直径。另外，比较P04 和P05 两次实验结果可以看出，实验P05 具有较高的撞击速度和两倍于前者的内压，但穿孔直径小于实验P04。这主要是由于实验P05 中的容器壁厚度略小于实验P04，可见容器壁厚度的微小差别导致的穿孔直径变化与内压的影响相比不可忽略。

总体来看，尽管不同工况实验中内压变化明显，但容器前壁穿孔直径改变量并不明显，最大差别仅3.46%，且明显受到撞击速度及容器壁厚度微小变化的影响。因而可以得到初步结论，内压变化对容器前壁穿孔直径的影响远小于撞击速度及容器壁厚度变化的影响。在实验中，压力容器加工精度、容器壁材料性能、弹丸发射速度等不可避免存在微小误差，导致对前壁穿孔直径随内压变化规律的判别难度较大。因此，本文中将基于数值模拟方法对此问题进行进一步分析。

关于容器前壁穿孔形貌，由图9 中Exp.1、Exp.2 的照片可知，穿孔边缘光滑，局部材料发生大变形，形成朝向容器壁内外两侧的翻边。观察发现，在4 个工况中，内翻边与容器前壁的夹角θ 明显不同，称θ 为内翻角，如图9(a)中第1 幅图片所示。图10 给出了图9 中每个工况两个剖面的内翻角平均值θ，由图10 可以看出，当内压从接近0 MPa 增高到2.2 MPa 时，内翻角θ 从37.2°增大到54.4°，可知内翻角与内压正相关（相关系数R=0.99），内翻角 θ随内压的增加而增大，撞击速度和容器壁厚度存在的微小差别对内翻角θ的影响并不明显。

图9 容器前壁穿孔截面Fig. 9 Cross sections of holes in front vessel walls

观察内翻边形貌，在实验P02 和P04 中，内压较低，内翻边整体凹向容器壁；而在实验P03 和P05 中，内压较高，内翻边凹向穿孔一侧，且如图9(b)中第1 幅图所示，当内压为2.2 MPa时，内翻边出现了反向弯折。上述现象均说明，内压越大，对超高速撞击穿孔内翻边向内弯折的阻力就越大。

为了检验数值模型的有效性，基于压力容器模型B，建立了4 个实验工况的数值模型。其中，因工况P02 的内压小于200 Pa，在数值模型中未设置气体及应力边界条件，忽略了气体的作用。将计算获得的前壁穿孔直径、内翻边形貌及内翻角等与实验结果进行对比。

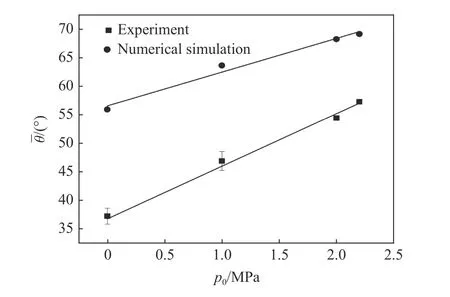
图10 内翻角θ 随内压p0 的变化Fig. 10 Variations of θ with p0

前壁穿孔直径的数值模拟结果见图8，所有工况均小于实验结果，误差介于24.5%～33.0%，较稳定。工况P05 和P03 的穿孔直径数值模拟结果相同，反映出工况P03 具有的较高内压对穿孔直径的影响抵消了较低撞击速度的影响，说明穿孔直径与内压成正比，但内压的影响并不显著。尽管数值模拟与实验结果存在一定差距，但由其获得的关于内压影响穿孔直径的结论与实验一致。

图9 中的第3 幅图给出了数值模拟的穿孔形貌，可以看出，随着内压增加，内翻边的形态由凹向容器壁一侧逐渐转变为凹向穿孔一侧，与实验现象一致。图10 中给出了数值模拟得到的内翻角θ 值，尽管与实验值相比较大，但同样表现为与内压呈正相关（相关系数R=0.99）。

以上比较说明，数值模拟结果与实验结果之间存在稳定的系统误差，分析其原因为实验中压力容器的铝合金可能与标称的材料标号及热处理状态不一致，实际材料强度低于6061-T6 铝合金的理论强度。尽管此系统误差影响数值模拟结果的准确值，但数值模拟得到的现象及规律性结果与实验结果一致，因此应用压力容器模型B，可进行内压对前壁穿孔形貌、穿孔直径等的影响规律与机理研究。

3 前壁穿孔数值模拟结果

为了进一步分析内充气体对压力容器前壁穿孔的影响，基于压力容器模型B，开展了多种参数下压力容器的超高速撞击数值模拟研究。压力容器外径为100 mm，壁厚为1.00 mm，弹丸直径为4.00 mm，撞击速度范围为1.00～9.00 km/s，内充气体压强范围为0～6.0 MPa。

本部分数值模型编号规则为：模型系列代号-撞击速度（km/s）-内压（MPa）。模型系列代号包括CI、CM、CG，CI 表示压力容器中包含内壁应力边界条件及局部气体模型；CM 表示仅在压力容器内壁施加了应力边界条件，无局部气体模型；CG 表示仅在压力容器内添加了局部气体模型，无内壁应力边界条件。

3.1 穿孔形貌

25 次CI 系列数值模拟结果显示，随着撞击速度的不同，容器前壁穿孔形貌可分为3 种类型，图11以撞击速度为1.00、3.00、7.00 km/s 的工况为例，分别给出这3 种典型形貌及其受容器内压的影响。

图11 CI 系列数值模拟穿孔截面Fig. 11 Cross section of holes in the numerical simulations using a series of CI models

当撞击速度较低时，如图11(a)所示，穿孔形貌为类型Ⅰ，即穿孔边缘材料的塑性变形较小，穿孔边缘光滑，在容器壁两侧仅形成环绕穿孔的塑性凸起，未出现明显的翻边现象。塑性凸起的高度低、厚度大，整体强度高，内充气体对其作用不明显，其形态并未随内压的变化而改变。

当撞击速度增大到一定程度时，如图11(b)所示，穿孔形貌转变为类型Ⅱ，即穿孔边缘的材料塑性变形较大，在容器壁两侧形成明显的翻边，穿孔边缘仍然保持光滑。内翻边厚度从根部向头部逐渐减小，强度降低，中部以上形貌受内充气体影响明显。如图11(b)所示，当无内充气体时，内翻边保持正常弯折角度；当内压为1.5 MPa 时，内翻边头部出现凹向穿孔一侧的形貌；当内压增加到3.0、4.5 和6.0 MPa 时，内翻边出现明显反向弯折，且弯折位置逐渐向根部靠近，图11(b)的第3 幅和第5 幅图中的反向弯折材料因单元变形过大而在数值模拟计算中被删除。这说明内压越大，内充气体对内翻边在形成过程中的反向阻力越大。

当撞击速度更高时，如图11(c)所示，穿孔形貌为类型Ⅲ，在容器壁厚度方向上包含中间楔形体与两侧翻边，穿孔边缘不再保持光滑。其形成的原因是，穿孔边缘材料发生严重的塑性变形，材料弯曲产生的应力超过材料强度，翻边根部与截面中心材料之间发生断裂。内翻边截面形状不规则，总体上看，可将内翻边从中间分为上下两部分：下半部分与容器壁相连，根部因发生断裂而导致厚度小于图11(b)所示的情况；上半部分厚度远小于下半部分。另外，随着内压增加，内翻边与楔形体之间的断裂位置从靠近容器壁内表面逐渐向容器壁厚度中心方向移动，导致内翻边根部的厚度总体上呈现逐渐变大的趋势。内翻边形状同样受到内充气体的影响，上半部分随内压增加发生反向弯折，且内压越大，反向弯折角度越大，图11(c)的第3 幅和第4 幅图中反向弯折部分因单元变形过大被删除。

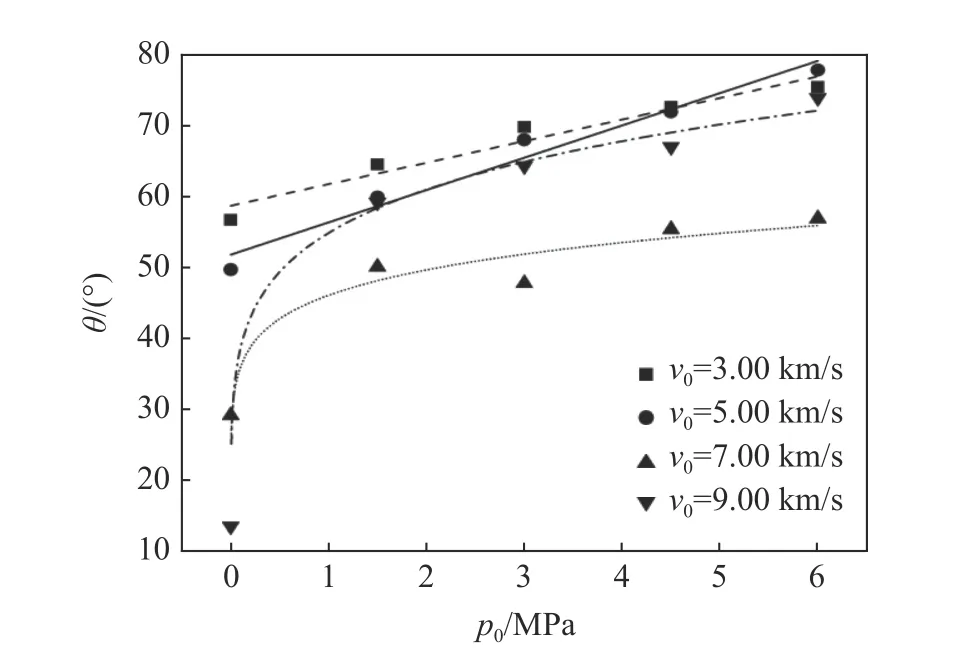
图12 CI 系列数值模拟穿孔内翻角θ 随内压p0 的变化Fig. 12 Variations of θ with p0 in the numerical simulations based on the CI models

图12 给出了除撞击速度为1.00 km/s 以外其他工况的内翻角θ。当撞击速度为3.00 和5.00 km/s 时，随着内压从零增加到6.0 MPa，内翻角值基本呈线性增大趋势，相关系数R＞0.97。当撞击速度为7.00、9.00 km/s 时，内翻角与内压整体呈非线性关系；但当内压介于1.5～6.0 MPa时，内翻角与内压之间线性关系较好；当内压介于0～1.5 MPa 时，内翻角变化速率更大。上述现象说明，对于穿孔形貌类型Ⅱ或Ⅲ且内压较高时，内翻边根部厚度较大且基本一致，内翻边的弯折程度主要受内充气体压强大小的影响，内翻角与内压呈线性关系；对于穿孔形貌类型Ⅲ，当内压较低时，内翻边根部厚度较小，其变化导致的强度改变较为明显，内翻边弯折程度同时受其强度与内压值的影响，呈非线性变化规律。

为了探究内充气体压强影响内翻角大小及造成内翻边反向弯折的具体机制，以v0=3.00 km/s、p0=6.0 MPa工况为例，利用压力容器模型B 对两种典型特征的建模方法，分别建立了两个数值模型：CM-3.00-6.0 与CG-3.00-6.0，将容器壁承受气体压力与容器壁后存在气体介质这两种影响因素解耦。图13 给出了模型CM-3.00-6.0、CG-3.00-6.0、CI-3.00-6.0 在同一时刻的内翻边形貌。图13(a)中，容器壁仅承受气体内压，内翻边出现明显反向弯折；图13(b)中，容器内仅存在与6.0 MPa 气体相同密度的无压力气体，内翻边呈现出凹向穿孔一侧的趋势，但并未反向弯折；图13(c)中，内翻边反向弯折程度大于图13(a)中的情况。三者比较说明，内翻边在形成过程中会以一定速度向容器壁方向转动，承受气体介质的气动阻力，但此作用力随着运动速度的降低而减小，对内翻边运动的影响小于气体内压的影响；内翻边的最终形貌是气体内压与气动阻力共同作用的结果，但气体内压产生的作用力为主要影响机制。

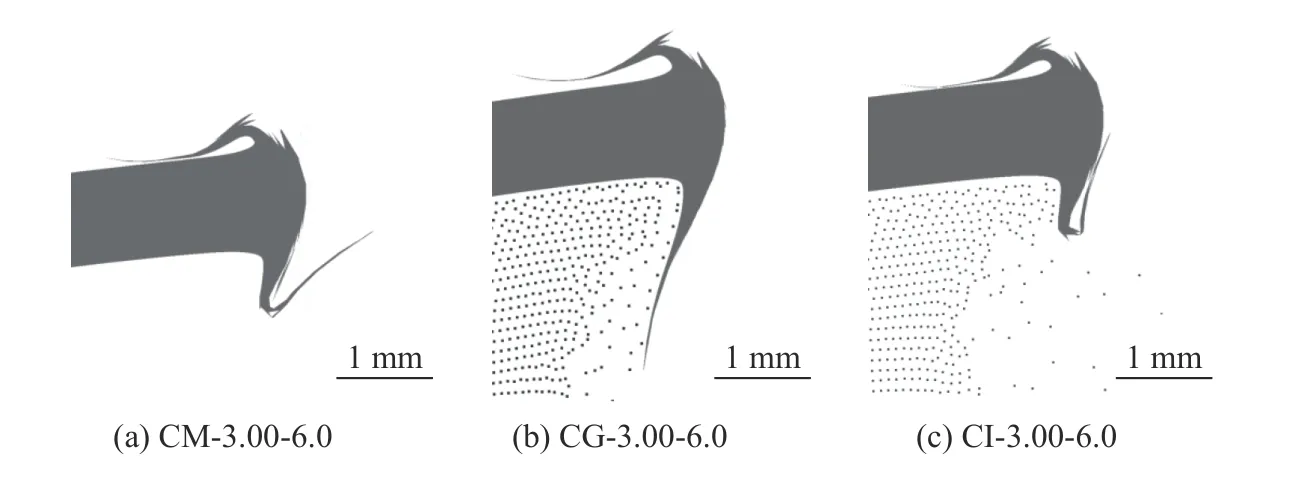
图13 3 种数值模型内翻边形貌比较（v0=3.00 km/s, p0=6.0 MPa, t=15 µs）Fig. 13 Comparison on inner flanging morphology among three types of numerical model (v0=3.00 km/s, p0=6.0 MPa, t=15 µs)

3.2 穿孔直径

图14 给出了25 个数值模拟工况的前壁穿孔直径。对于边缘不光滑的穿孔形貌类型Ⅲ，穿孔直径dh指楔形体之间的最小距离，如图11(c)的第1 幅图所示。

图14 CI 系列数值模拟穿孔直径dh 随内压p0 的变化Fig. 14 Variations of dh with p0 in the numerical simulations based on the CI models

图15 给出了不同形貌类型穿孔的Δdh与内压的关系。图15(a)中穿孔形貌为类型Ⅰ和Ⅱ（撞击速度为1.00～5.00 km/s），此类穿孔边缘光滑，孔径测量误差小；图15(b)中穿孔形貌为类型Ⅲ（撞击速度为7.00 和9.00 km/s），此类穿孔边缘不规则，孔径测量值随机误差较大。分别对图15(a)和图15(b)中的数据进行线性拟合，相关系数R 分别为0.95 和0.84，均说明穿孔直径与容器内压相关性强，其中图15(b)中相关系数相对较低的原因是在孔径变化很小的情况下，不规则孔边缘带来的随机测量误差影响较大。

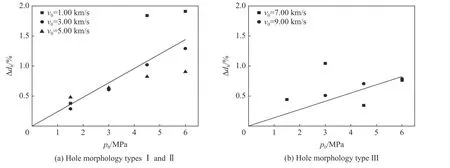
图15 CI 系列数值模拟中Δdh 随内压p0 的变化Fig. 15 Variations of Δdh with p0 in the numerical simulations based on the CI models

图15 中Δdh与内压的关系为：

由式(2)可知：穿孔直径随内压的增加而增大。

内充气体对前壁穿孔直径的作用机制可能来源于两个主要因素：容器壁内存在的薄膜应力和容器壁后存在的气体介质。为此，借助CM-3.00-6.0 与CG-3.00-6.0 模型将两种机制解耦，与无内充气体作用的压力容器模型及CI-3.00-6.0模型的计算结果进行对比分析。图16 给出了4 种模型中穿孔直径dh的时间历程曲线，在4 种模型中，弹丸撞击容器前壁后，在2.8 µs 左右穿孔直径达到最大值，然后经历较大幅值的弹性震荡过程，在60 µs 之后震荡幅值减小，可认为孔径基本达到稳定。由图16 可知，CM-3.00-6.0、CG-3.00-6.0、CI-3.00-6.0 模型的孔径均大于无气体作用模型，且从最大值开始各孔径随时间的变化趋势基本一致，因此，前3 种模型中各因素对孔径的作用主要体现在影响了穿孔形成初期孔径最大值。

由于容器直径远大于弹丸直径，撞击点处的容器壁曲率较小，近似为薄平板。基于薄板穿孔理论[10-11]，可将穿孔的形成分为两个阶段：第1 阶段，在弹壁开始接触的极短时间内，产生近似平面冲击波，压缩材料向容器壁内表面运动，形成初始穿孔；第2 阶段，冲击波开始沿容器壁面内运动，压缩材料产生扩孔作用，最后衰减为弹性波，扩孔结束。第一阶段中的冲击波在容器壁内表面反射形成稀疏波，同样会在容器壁面内运动，“追赶”并卸载面内冲击波对材料的压缩。若容器壁内侧存在气体，其波阻抗大于零，反射稀疏波幅值比无气体时低，对面内冲击波的卸载程度相对较弱。因此，CG-3.00-6.0 模型中的最大孔径大于无气体作用情况，但由于铝合金的阻抗远大于6.0 MPa 气体的阻抗（约554 倍），其影响并不显著。

在CM-3.00-6.0 模型中，孔径比无气体作用时大的可能原因为，容器壁内已存在薄膜拉应力，穿孔从出现到孔径达到最大值的短时间内，孔边缘区域应力重新分布，开始产生环向拉应力，有助于扩大孔径。但因短时间内应力值较低，扩孔效果有限，由图16 可知，相对于容器壁内侧气体阻抗带来的冲击波强度变化，薄膜应力的扩孔效果更弱。

相对于无气体作用时的孔径，CM-3.00-6.0 与CG-3.00-6.0 两种模型中的孔径增加值之和为0.034 mm，而综合两种影响因素的CI-3.00-6.0 模型中的孔径增加值为0.067 mm。这说明两种因素并非独立影响穿孔，存在耦合效应，使得二者综合作用时的孔径大于单独作用时的线性叠加值。

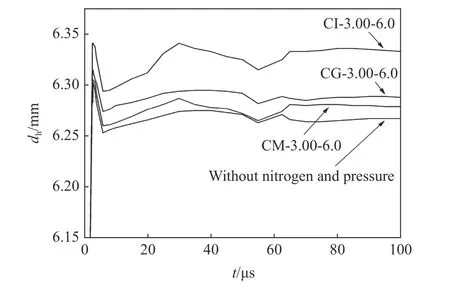
图16 穿孔直径dh 的时间历程曲线（v0=3.00 km/s，p0=6.0 MPa）Fig. 16 Variations of dh with time (v0=3.00 km/s, p0=6.0 MPa)

4 气体冲击波及其作用的数值模拟结果分析

球形压力容器前壁被撞击穿孔后，碎片云高速运动并压缩气体形成冲击波，在内压及气体冲击波作用下，穿孔边缘可能会形成较大的环向拉应力，若存在裂纹，则当应力值达到裂纹失稳扩展阈值时，容器前壁将会自穿孔边缘撕裂。为了分析碎片云与气体相互作用对前壁穿孔边缘环向应力 σh的影响，基于压力容器模型A，开展了多个工况的数值模拟。为了减小计算量，容器外径为50.0 mm，壁厚为0.5 mm，弹丸直径为4.0 mm，内压为3.0 和6.0 MPa，撞击速度为1.00、3.00 和5.00 km/s。

以内压3.0 MPa、撞击速度3.00 km/s 的工况为例，冲击波在容器内气体中的传播过程如图17 所示。为了排除弹丸撞击容器前、后壁产生的应力波在容器壁内传播带来的影响，对模型进行处理。当高压气体与容器壁达到静力平衡后，删除以撞击点为中心，稍大于弹丸直径的圆形区域内的前壁材料，如图17(a)所示。开始弹丸撞击计算，待弹丸前端运动到距离后壁1.0 mm 时，手动删除弹丸，仅剩余气体及容器壁模型继续计算，如图17(c)所示。对于所有工况，前壁圆孔直径取2.2 mm，与实际撞击穿孔尺寸不同，将其作为一个统一标准，评价气体冲击波对相同位置应力幅值的影响。

弹丸高速运动压缩气体形成典型的锥形冲击波如图17(b)所示。弹前冲击波S1 与弹丸保持相同的速度向后壁运动；侧向冲击波S2 以相对较低的速度侧向传播，其压缩的气体介质在短时间内即被卸载，随着传播距离的增大，波阵面增大，能量被分散；S2 在形成初期便开始与容器前壁相互作用，反射形成冲击波S3，向后壁运动。当S1 到达容器后壁后，便开始反射形成冲击波S4，向前壁运动，如图17(d)所示。待S2 完全到达容器壁侧后方时，反射形成朝向弹道中心传播的冲击波S5，如图17(e)所示。S3、S4、S5 各自运动，继续与容器壁相互作用形成新的冲击波，并在传播过程中能量逐渐耗散。图17 中弹道附近气体压强升高的原因为，弹丸压缩导致此区域内气体温度升高，内能增加，根据数值模型所采用的理想气体状态方程，压强随内能增加而增大。

图17 气体冲击波运动过程（p0=3.0 MPa, v0=3.00 km/s）Fig. 17 Shock wave propagation in the gas (p0=3.0 MPa, v0=3.00 km/s)

在冲击波传播过程中，容器壁中的应力状态受其影响而产生变化，图18 为两种内压工况前壁圆孔边缘的环向应力在弹丸相同速度撞击下前200 µs 的时间历程曲线。结合冲击波传播过程分析，可将应力历程分为3 个阶段。

阶段Ⅰ为冲击波产生开始，至冲击波S2 全部到达容器壁侧后方的过程。在此过程中，冲击波S2 先后作用于容器前后壁上两个较窄的环形区域上，作用过程清晰，主要在容器壁中产生拉压周期变化的环向应力。因此，图18 中显示前壁圆孔边缘处环向应力呈现为规则的大周期变化，这是冲击波S2 作用于容器前壁的结果。另外，最初的高频应力震荡是由手动删除材料引起的。

阶段Ⅱ为阶段Ⅰ结束时刻至冲击波S4 完成与容器前壁作用的过程。在阶段Ⅱ初期，冲击波S2 剩余部分整体作用于容器侧后壁，反射形成S5。在阶段Ⅱ中期，所有气体冲击波基本未与容器壁接触，容器壁内已产生的应力自由传播并相互作用。在阶段Ⅱ后期，冲击波S4 开始持续作用于前壁。整个过程中，冲击波与容器壁作用过程复杂，导致圆孔边缘环向应力持续震荡。图18 中的PS4点为冲击波S4 作用于圆孔附近容器壁时σh的幅值。

阶段Ⅲ为冲击波S4 在前壁产生的反射波完全脱离前壁之后的过程。容器内的各气体冲击波状态及其对容器壁的作用更为复杂，叠加容器壁内已存在的应力波动，圆孔边缘的应力震荡更加无规律。考虑到冲击波能量不断耗散，本文未对此阶段及以后过程进行分析。

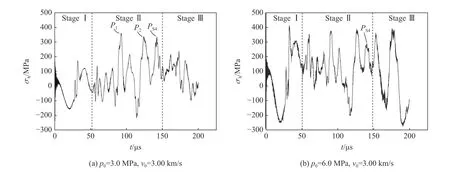
图18 环向应力 σh的时间历程曲线Fig. 18 Variation of σh with time

由图18 可见，环向应力历程中通常出现多个幅值与最大值σh,max接近的时刻，主要集中在阶段Ⅱ，如图18(a)中的P1、P2、PS4，其中前两点在冲击波S4 到达前壁（PS4点）之前就已出现。在图18(b)中，PS4点甚至低于其他几个幅值高点，且差距较大。可见，冲击波对前壁穿孔边缘应力的贡献，不仅体现于冲击波S4 在穿孔附近的作用，还包括其他时刻容器壁内应力波的传播与相互作用，导致应力出现多次大幅值高点。在其他工况的数值模拟中，也发现类似现象。

图19 给出了本文研究范围内6 个工况的σh,max。由图19 可以看出：σh,max 随撞击速度 v0的增大而增大，但增大的速率减小；另外，σh,max亦随容器内压 p0的增加而增大，但增大的速率与内压 p0成反比。以上数据仅作现象与规律分析，由于实际航天器用球形压力容器具有更大的直径与内压，因而存在多种影响前壁承受的气体作用力的机制：直径越大，内压形成的初始环向应力越大，但气体冲击波能量耗散更严重，可能减弱其对环向应力的影响；内压越大，初始环向应力越大，冲击波的作用也更明显；弹丸在实际撞击前壁时会破碎形成碎片云，相对于本文中采用的完整弹丸，其能量更分散，速度降低得比较快，产生的冲击波强度较低。

分析过程中，未考虑容器后壁被弹丸撞击损伤，适用于碎片云在高压气体中做减速运动而无法到达后壁的情况。若碎片云能够对后壁造成撞击损伤，后壁损伤应发生于冲击波S2 到达侧后壁之前，根据图18，此时前壁穿孔边缘环向应力历程处于阶段I，尚未出现由气体作用引起的多次大幅值应力；另外，后壁撞击损伤区同时遭受冲击波S1 的直接作用，承受载荷较大，并且后壁由碎片云造成的穿孔更不规则，裂纹失稳破坏阈值更低；因此，相对于前壁破裂，充气压力容器后壁破裂所需内压更低，这个分析结论与实验观察现象[1]一致。

图19 不同撞击速度和内压下的最大环向应力 σh,maxFig. 19 Variation of σh,max with impact velocity and initial pressure in the vessel

5 结 论

针对内充气体压强对球形压力容器前壁损伤的影响，开展了球形弹丸超高速撞击实验和数值模拟研究，得到如下结论：

（1）在撞击速度高于一定值后，高压气体的存在会影响容器前壁穿孔边缘内翻边的形貌，内压越高，内翻角越大，甚至出现内翻边反向弯折现象。

（2）前壁穿孔直径与内充气体压强正相关，但气压的影响很小，弹丸尺寸与速度、容器壁厚度等是前壁穿孔的决定性因素；研究气压对碎片云及其毁伤能力、气体喷射对周边设备的影响更具有工程价值。

（3）高压气体存在的主要特征为，气体压力作用于容器壁及容器壁内侧存在一定密度的气体介质，气压对前壁穿孔形貌及孔径的影响是二者综合作用的结果。

（4）在前壁穿孔边缘，因气体冲击波产生的环向应力最大值随撞击速度和内压的增加而增大；但并不一定是由从后壁反射的冲击波作用于穿孔附近时产生，亦可能是其他冲击波作用导致的容器壁内应力波传播及相互作用的结果。