二维空间离散化的FitzHugh-Nagumo格点系统的全局吸引子的上半连续性

姜 红

（商丘工学院，河南 商丘 476000）

1 引言

无穷维动力系统在很多领域上有广泛的应用，主要是研究具有耗散性的动力系统当时间趋于无穷大时的渐近行为.一般都是通过全局吸引子来描述, 因而全局吸引子成为研究的重点.研究全局吸引子又要通过研究动力系统解的结构来体现.本文是在证明了二维空间离散化的FitzHugh-Nagumo格点系统的全局吸引子([1])的存在性的基础上研究其上半连续性。

2 主要工作

在本章中,我们研究如下二维空间离散化的FitzHugh-Nagumo格点系统

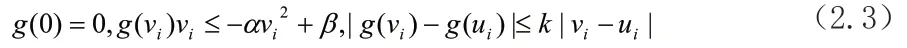
为了研究全局吸引子的上半连续性，我们先证明当0→ε时，全局吸引子εA是一致有界的。这也是本文的主要工作.

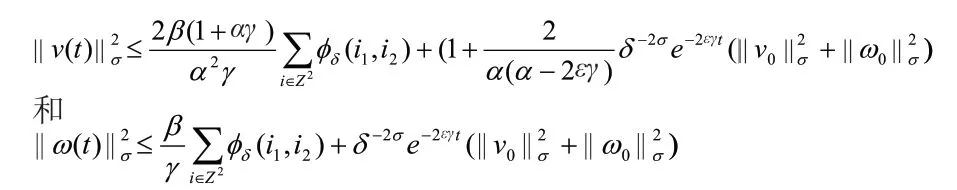
其中，β,α满足文献([1]).

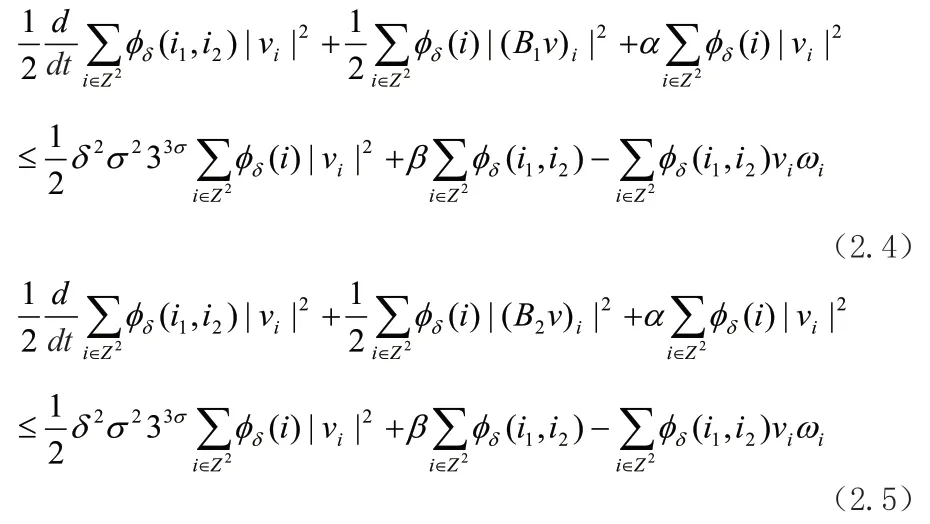
相加，得

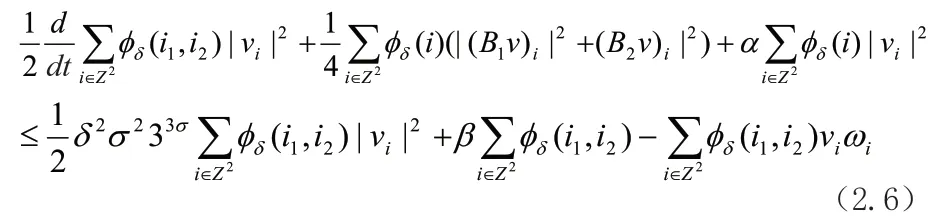
由（文献[1]）中的（2.1.5）可得，式子（2.6）右边第一项是有界的

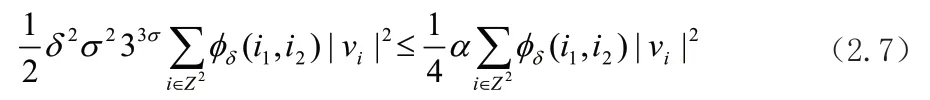
且（2.6）右边最后一项满足

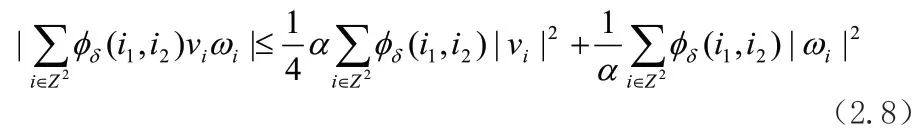
由（2.6）-（2.8）可得

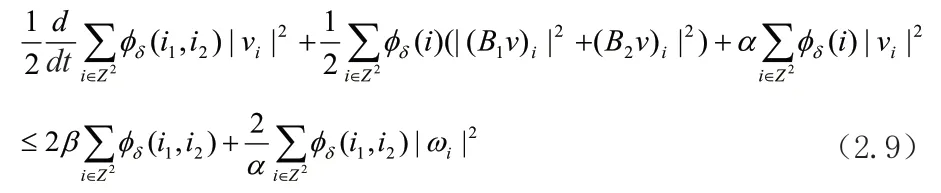
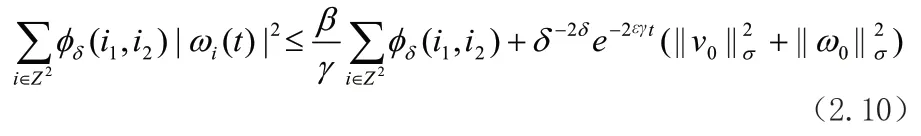
将（2.10）代入（2.9），有

既而

3 总结

本文为证明全局吸引子的一致有界性做了铺垫，下一步读者可考虑证明全局吸引子的一致有界性。