某沉管隧道洞口减光建筑通风特性分析

杜江梅

(云南省交通投资建设集团有限公司，昆明 650200)

由于沉管隧道具有不影响航运、天气适应性强等特点，已逐步成为跨越大面积水域的首选方案。沉管隧道一般暗埋里程较长，车辆通过隧道出入口时，驾驶人会经历明暗交替变化的视觉冲击[1]，极易产生“眩晕”与“瞬盲”，行车安全隐患较大[2]。针对这一问题，国内外较为普遍的做法是设置洞口减光建筑[3]。

目前，国内外针对减光建筑的研究主要围绕遮光棚亮度、材料折光率、驾驶人适应性等方面[4-6]。但隧道洞口减光建筑的设计除要满足视觉适应需求外，还应兼顾隧道通风效果。由于沉管隧道结构特点，不同行车方向的进、出口间距很小，出口方向排出的气体污染物极易被相邻进口吸入造成“二次污染”，因此，对其通风特性的研究极为必要。而目前有关隧道洞口减光建筑通风特性的研究多集中于通风型式的定性分析，缺少对通风特性及污染物窜流规律的定量计算。汤召志[7]采用数值模拟方法，分析了减光建筑隔墙长度和顶棚镂空面积对隧道进、出口污染空气窜流形式的影响。杨秀军等[8]采用数值模拟手段对沉管隧道洞口减光建筑不同形式下的污染物窜流量进行了计算。彭余华等[9]运用标准k-ε双方程模型，得到了毗邻隧道洞口减光建筑污染物扩散规律。傅向祥[10]采用CFD方法分析了不同通风开口方案的隧间减光建筑通风特性，得到了其通风开口高度的最优设计值。综上所述，现有减光建筑通风特性的研究对象主要是普通公路隧道，针对洞口相邻、浅埋的沉管隧道，其洞口减光建筑通风特性的适用性缺乏实验室相似模型对比验证，计算结果存在不确定性。

为此，本文针对沉管隧道出口特点，制定减光建筑设计方案，建立SST-组分运输模型，通过室内相似试验对模型进行了验证，并以某海底沉管隧道为研究对象，定量分析了大断面沉管隧道洞口减光建筑不同设计方案对其通风效果的影响，得到减光建筑通风特性及污染物窜流规律，以期供类似沉管隧道洞口减光建筑设计参考。

1 减光建筑设计

常用隧道洞口减光建筑形式主要有遮光棚和遮阳棚2种[11]。其中遮阳棚因其顶部封闭，遮阳效果好、可适应多种复杂天气环境，非常适合沉管隧道。但由于全封闭的环境对隧道的通风设计影响较大，因此在减光建筑设计过程中需考虑洞口通风特性。

减光建筑结构可分为钢结构和钢筋混凝土结构2种。钢筋混凝土结构减光建筑耐久性强、运营成本低，但对洞口亮度调节能力较差。钢结构减光建筑施工方便、通用性强，但运营期间维护成本高。结合沉管隧道出口暗埋的特点，其洞口减光建筑设计采用“钢筋混凝土-钢结构”组合模式。底层采用钢筋混凝土结构与隧道洞口连成一体，便于维护；上层部分采用钢结构形式，充分发挥其镂空特点，增强隧道的通风性能，且在紧急情况方便逃生、救援。

隧道洞口减光建筑设计长度S可依据以下公式计算[12]：

(1)

式中：D为隧道进出口照明过渡段长度，m，可根据国内公路隧道照明标准取值；V为隧道设计速度，km/h；T为视觉适应时间，根据该海底隧道最不利情况洞内外照度差69 000 lx，取值为17 s[13]。由此，计算可得不同设计速度时隧道洞口减光建筑设计长度，如表1所示。

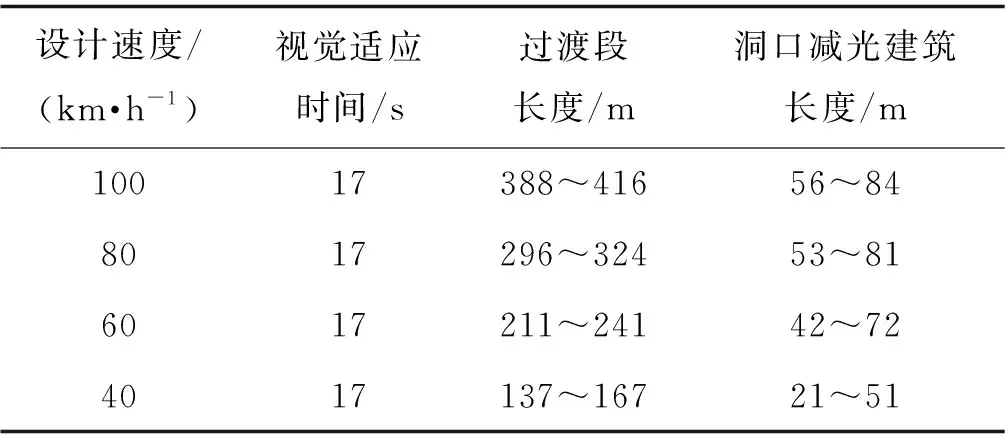
表1 隧道洞口减光建筑长度合理设计参数

本文以某海底沉管隧道洞口遮阳棚减光建筑通风设计为依托，该隧道洞口为双向12车道，断面为矩形，设计减光建筑净高7.85 m～10.66 m，净宽57 m，坡度2.3°。沉管隧道设计速度100 km/h，对照表1可知，其洞口减光建筑设计长度为56 m～84 m。减光建筑顶棚采用蓝色有机玻璃遮阳棚，以便隧道洞口亮度可控；中间设置隔墙；两边边墙镂空，由于下部边墙与隧道相连，仍处于暗埋段，因此镂空只能设计在边墙上部。其三维设计如图1所示。

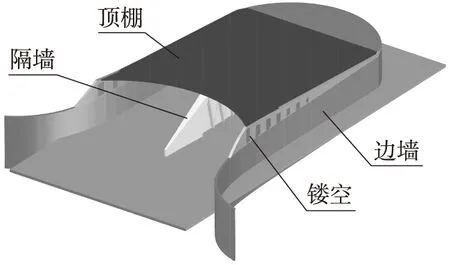
图1 某海底沉管隧道洞口减光建筑三维设计

根据该海底沉管隧道工程实际情况，分析减光建筑3个主要设计参数对其通风特性及污染物窜流规律的影响。具体设计如下：1) 隔墙长度分别为0 m、14 m、28 m、42 m、56 m；2) 减光建筑长度分别为56 m、63 m、70 m、77 m、84 m；3) 边墙镂空面积分别为0 m2、30 m2、40 m2、50 m2、60 m2。共15种设计工况。

根据实测隧道洞内车辆通行条件下全年风速平均值，拟定右线进口风速为7.0 m/s，左线出口为4.7 m/s。隧道洞口污染物窜流的计算区域为减光建筑外30 m×139 m×80 m。根据现场初步勘测数据，计算区域是大气环境，静压力为101.325 kPa。全年大多数情况，洞外自然风速为0.1 m/s～0.5 m/s。隧道内全年平均温度为27 ℃，空气密度为1.165 kg/m3，动力粘度为1.845×10-5Pa·s，重力加速度为9.8 m/s2，比热容为1 005 J/(kg·K)，导热系数为0.025 6 W/(m·K)，壁面粗糙度为0.022。隧道出口污染物包括CO、氮氧化物、SO2及PM 2.5等。由于CO浓度的测量比其他污染物更准确，且各污染物分布大致相同，因此CO的浓度分布即可代表污染气流的分布，故本文选择CO作为代表，对污染物分布特性进行分析。现场测定出口污风中CO浓度为20 cm3/m3，进口及大气为新鲜风。

2 风流分析模型

由于标准k-ε模型计算量适中，且已有较多试验数据验证，其在通风特性计算中应用广泛[14]。但标准k-ε有2个不足：1) 耗散低、特征长度大，导致压力梯度流中的剪切应力计算偏大；2) 需要使用低雷诺数阻尼函数进行近壁面修正。近年来，各种风洞试验表明，与标准k-ε模型相比，SST模型更适于研究空气边界层中的流动[15]。

SST模型是一个两方程模型，结合了内边界层模型和边界层外区域模型。在边界层内部通过公式使模型适用范围从粘性层扩展到近壁面，因此SST模型可精确计算远离壁面充分发展的低雷诺数湍流，如隧道通风。SST模型通过联合近壁区域k-ω模型和自由剪切层的改进k-ε模型进行计算，实现步骤为：1) 将原始k-ω模型乘以混合函数F1；2) 转换后的k-ε模型乘以(1-F1)；3) 将两者相加。模型之间的切换调用由混合函数F1控制，其在近壁区为1(k-ω模型)，在自由剪切层则向0趋近(k-ε模型)，从而实现近壁区域k-ω模型到自由剪切层k-ε模型之间的过渡。此外，考虑到湍流剪应力传输效应在逆压流动计算中的重要性，引入了涡粘性修正。SST模型表达形式如下：

(2)

(3)

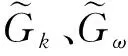
φ=F1φ1+(1-F1)φ2

(4)

本例混合气体中的各组分之间不发生化学反应，因此可采用多组分运输模型，其组分输运方程为：

(5)

式中：mj为第j种物质的质量分数，所有废气的质量分数之和为1；Smj是单位容积内组分j的生成率，假设无其他新污染源，则其值为0。本文以CO气体代表污染物，与空气混合进行计算，隧道内各气体组分的基本参数如表2所示。

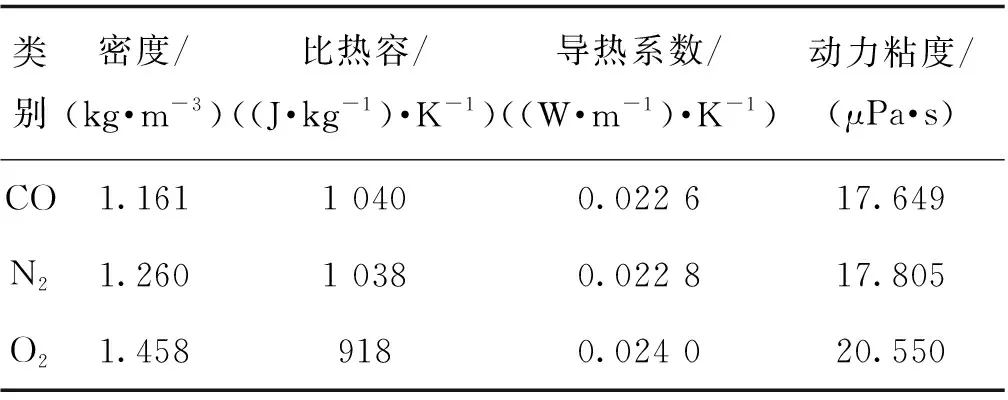
表2 减光建筑内各气体参数

此外，隧道洞口减光建筑内的气流流通和污染物扩散还受质量、动量和能量守恒方程的控制。本文采用有限体积法对上述方程组联立求解。

3 模型验证

为了验证SST模型的可靠性，进行了不同工况下隧道污染物窜流规律相似模拟试验研究，试验装置如图2所示。以Froude准则为依据，参考国内外学者建立的相似模拟试验系统，以前述某海底隧道工程实例为原型，在室内搭建了1/20 减光建筑模型，进行通风特性试验分析。减光建筑模型高0.39 m～0.53 m，宽2.85 m，长3.5 m，坡度2.3°。单个隧道模型的宽度为1.4 m，远大于美国消防协会得到的模型试验最小尺度0.3 m[16]，气流可充分发展，保证了试验结果的准确性。试验共设置不同进口风速、洞外风速、隔墙长度的12组工况，试验结果如表2所示。模型选用材质与实际设计相同，通过风机将按比例混合好的风流从隧道出口送出，同时在隧道进口匀速吸入。利用传感器实时采集风速及CO浓度。待风速及浓度稳定后，记录风速及CO浓度值，并计算出CO窜流率λ，计算公式如下：

(6)

式中：Qin为进口窜入的CO量；Qout为出口排出的CO量。

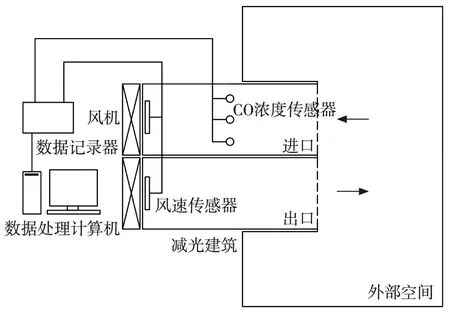
图2 试验装置

采用SST-组分运输模型对各试验工况进行计算，同样得到CO窜流率λ的值。模型计算结果与试验结果的对比如表3所示。从表3数据可以看出，计算结果与实测值的最大偏差为5.2%，属于±6%的允许误差范围，表明本文采用的数学模型合理，使用该数学模型进行实际工况隧道通风特性分析准确、可靠。

4 结果分析

以该海底沉管隧道为例，为定量分析减光建筑设计形式对其通风特性及污染物窜流规律的影响，采用SST-组分运输模型对隧道出口减光建筑风流情况进行计算，并导出各计算工况中距该海底沉管隧道洞口35 m(纵向Z=-35 m)截面处，离地高度分别为1.5 m、4.5 m、7.5 m处的CO浓度值。

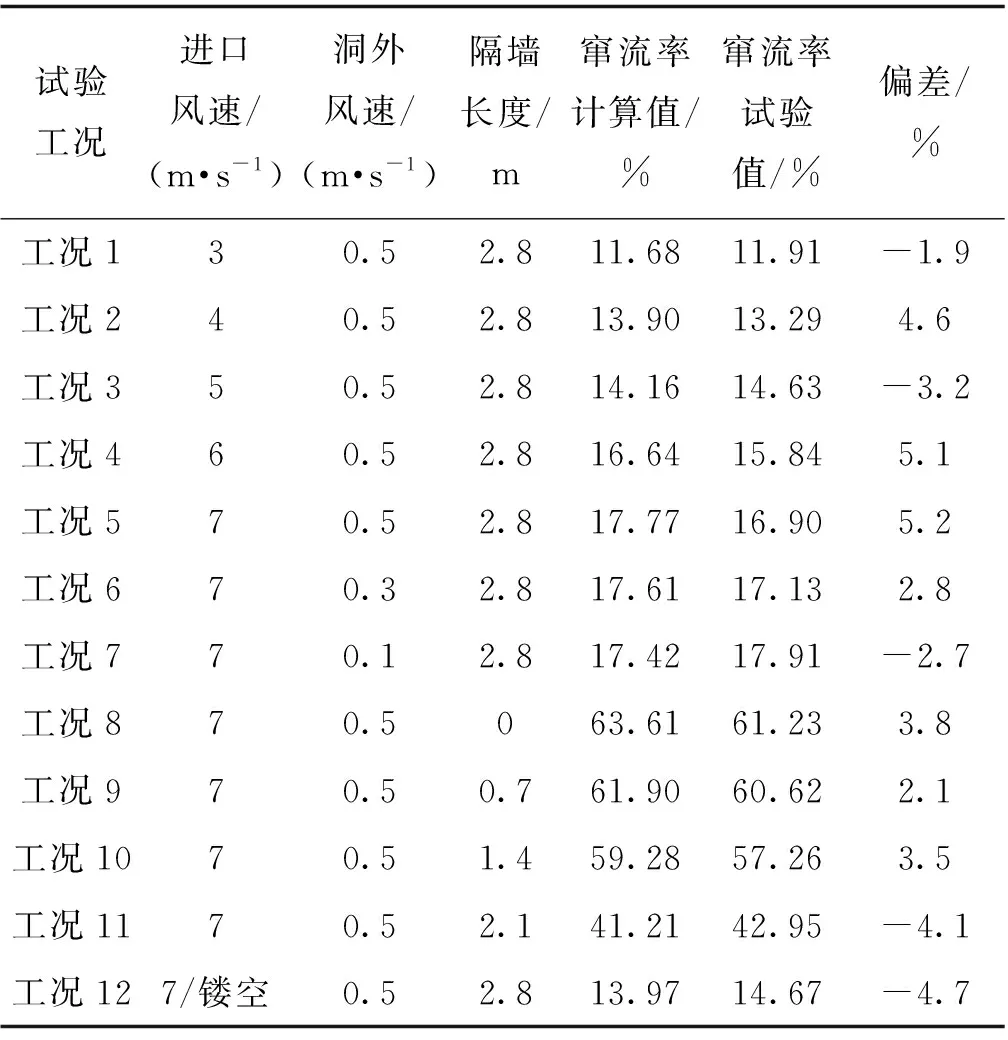
表3 试验结果

4.1 中间隔墙对风流的影响

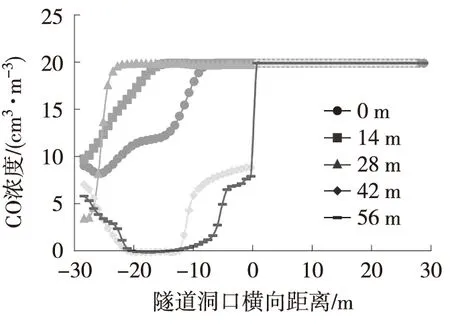
不同隔墙长度减光建筑距该海底沉管隧道洞口35 m(纵向Z=-35 m)截面不同高度处的CO浓度如图3所示。隧道洞口横向距离0 m～30 m为隧道出口侧，风流中CO浓度为20×10-6cm3/m3，隧道洞口横向距离0 m～-30 m为隧道进口侧。由图3可以看出，隧道出口的污染物会对进口的洞内环境造成污染。提取隧道进口侧不同位置的CO浓度，如表4所示。设置隔墙后，隧道进口中部及顶部的CO浓度显著降低，分布范围也明显减小，中间几乎没有污染物。这主要是由于减光建筑无中间隔墙时，负压区仅集中在隧道出口附近，导致减光建筑外的新鲜空气无法吸入。设有中间隔墙时，隔墙两侧形成了均匀的负压带，可保证进口有效吸入减光建筑外的新鲜空气，从而减少对出口污风的吸入。

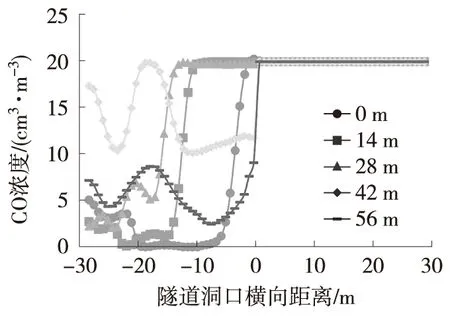
(a) 底部Y=1.5 m

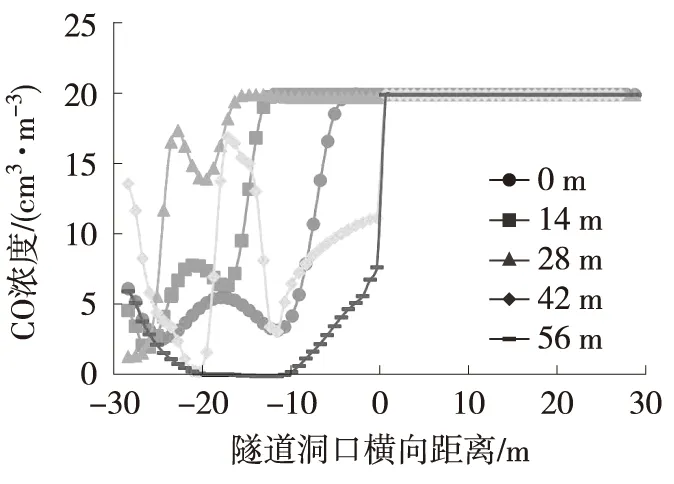
(b) 中部Y=4.5 m

(c) 顶部Y=7.5 m

为进一步评价隧道洞口减光建筑污染物扩散特征，以该海底沉管隧道为例，采用窜流率对计算结果进行定量分析，如图4所示。结果表明，中间隔墙设计长度低于28 m时，污染物窜流率保持在66.5%以上。当隔墙设计长度分别为42 m、56 m时，污染物窜流率分别降低至43.1%、17.7%。由图4可见，设置隔墙对于改善隧道进口侧的空气环境有很大帮助，且长度应尽可能长。

4.2 减光建筑长度对风流的影响

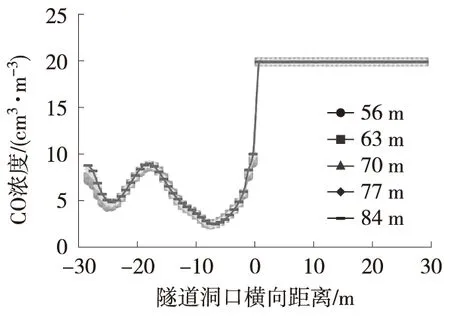
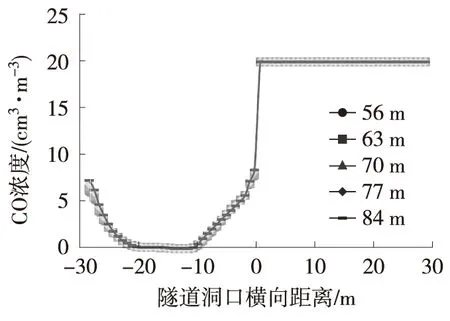
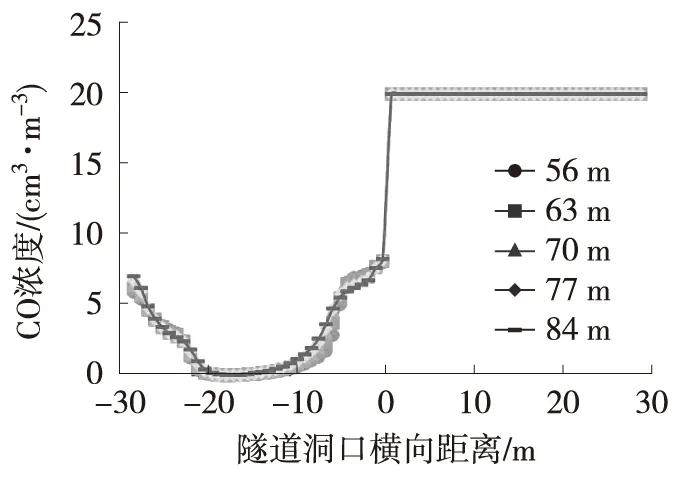
不同长度减光建筑距该海底沉管隧道洞口35 m

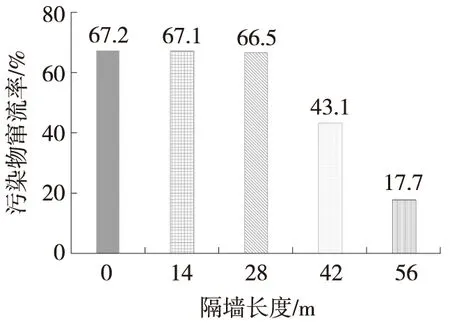
图4 不同隔墙长度减光建筑污染物窜流率

(纵向Z=-35 m)截面不同高度处的CO浓度如图5所示。在减光建筑底部水平截面上，隧道进口CO浓度在左侧、中间、右侧达到峰值，而在中部、顶部水平截面上则呈两侧高、中间低的分布特征。隧道进口不同位置的CO分布情况如表4所示。从表4可知，减光建筑长度变化对隧道进口污染物分布影响不大。

采用窜流率针对不同长度减光建筑对进出口污染物的影响结果进行定量分析，如图6所示。结果表明，减光建筑长度为56 m、63 m、70 m、77 m、84 m时，污染物窜流率分别为17.7%、17.9%、18.2%、18.3%、18.5%。由此可进一步验证上述结论，即设计速度100 km/h的矩形大断面隧道洞口减光建筑长度变化对隧道相邻进口污染物窜流影响不大；对隧道整体通风效果进行分析，减光建筑长度较小时，进口风速较快，形成明显的剪切效应，出口风流更容易进入进口，对其造成污染。而减光建筑长度较大时，风流沿程损失增加，须在进口增加通风设备以保证风量，导致通风效率低。为了减少污染物窜流产生的二次污染，同时减少不必要的压力损失，实际工况下隧道洞口减光建筑长度最优值建议取长度设计值范围的中值。

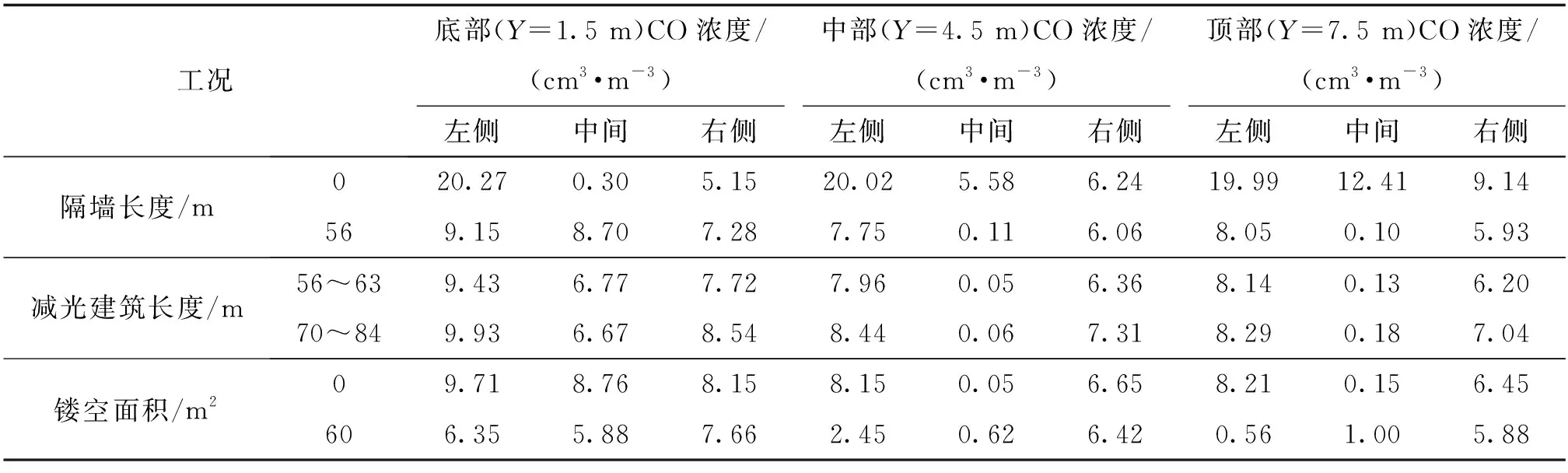
表4 右线进口污染物分布情况

(a) 底部Y=1.5 m

(b) 中部Y=4.5 m

(c) 顶部Y=7.5 m

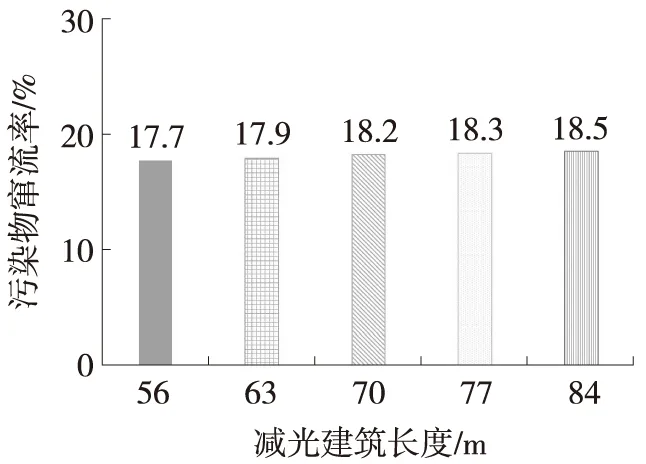
图6 不同长度减光建筑污染物窜流率

4.3 边墙镂空对风流的影响

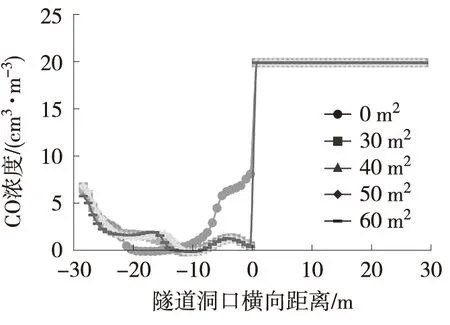
不同边墙镂空面积减光建筑距该海底沉管隧道洞口35 m(纵向Z=-35 m)截面不同高度处的CO浓度如图7所示。隧道进口不同位置的CO分布情况如表4所示。由图7可见，减光建筑边墙镂空可显著降低隧道进口底部、中部及顶部左侧的CO浓度，从而有效改善进口污染情况。这主要是由于减光建筑进口侧边墙镂空后，外部新鲜风流大量流入进口，从而减少了对相邻出口污风的吸入。此外，减光建筑边墙镂空后，出口、进口风流通道增加，风流易于流通，隧道洞口负压较小，整个减光建筑的压损较小，通风效率高。

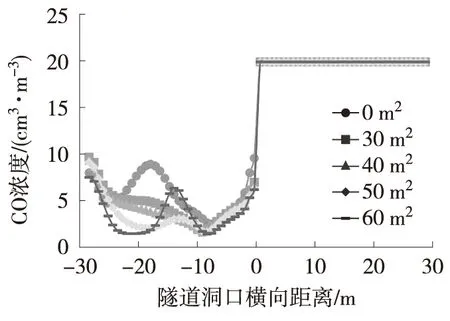
(a) 底部Y=1.5 m

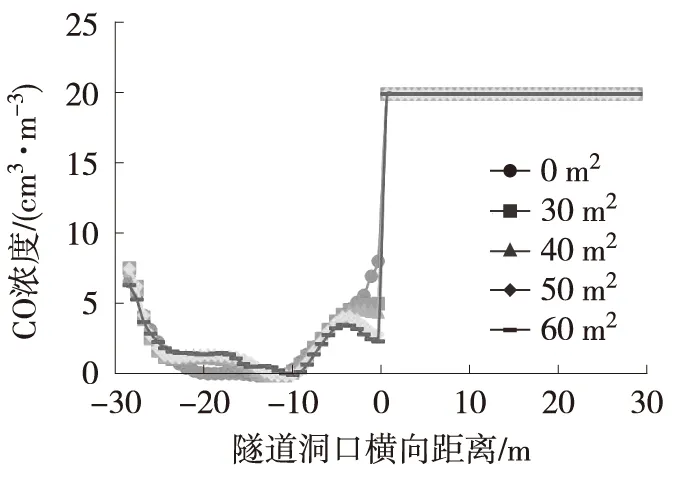
(b) 中部Y=4.5 m

(c) 顶部Y=7.5 m

采用窜流率针对不同边墙镂空面积减光建筑对污染物的影响结果进行定量分析，如图8所示。结果表明，相较于70 m长度减光建筑边墙不镂空时，边墙镂空可将污染物窜流率从18.2%降至12.5%，且随着边墙镂空面积增加，污染物窜流率线性降低。对于其他长度减光建筑的计算结果也与此相同。综上所述，在减光建筑两侧边墙进行镂空，可有效减少污染物窜流产生的二次污染，同时降低风流压损，提高通风效率。

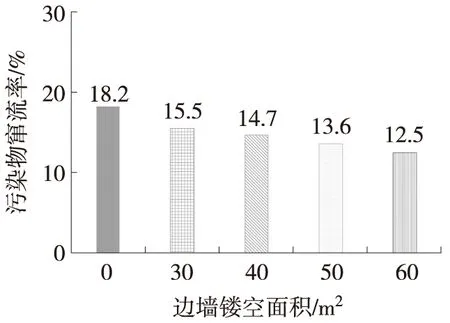
图8 不同边墙镂空面积减光建筑污染物窜流率

5 结论

1) 在减光建筑中间设置隔墙，可在其两侧形成均匀负压带，保证其进口侧有效吸入减光建筑外的新鲜空气，从而有效降低污染物窜流率。

2) 减光建筑长度较小时，出口风流更易进入进口，对其造成污染。而减光建筑长度较大时，风流沿程损失增加，导致通风效率低。综合考虑，减光建筑长度最优值建议取长度设计值范围的中值。

3) 随着边墙镂空面积增加，污染物窜流率线性降低。减光建筑两侧边墙镂空可有效减少污染物窜流产生的二次污染，同时降低风流压损，提高通风效率。