孔径比和动量比对双股射流撞击式雾化影响分析①

王宇奇，勾文进，陈明慧，张 帅，郑 耀

(1.浙江大学 航空航天学院，杭州 310027；2.上海飞机设计研究院，上海 201210)

0 引言

双股射流撞击雾化喷嘴具有结构简单、制造成本低、雾化性能较好、混合效率高等优点，已广泛应用于液体火箭发动机中。喷嘴的雾化过程会影响后续的蒸发、燃烧过程，继而影响发动机的燃烧效率与燃烧稳定性。因此，针对双股射流撞击式的雾化过程与雾化机理的研究对于发动机的设计具有重要意义。

已有双股射流撞击式喷嘴雾化特性研究以实验手段为主。Heidmann等[1]对射流撞击进行了大量实验研究，揭示了不同射流速度、喷嘴直径以及流体性质对喷雾结构的影响。Dombrowski等[2]对液膜破碎的原因进行了研究，研究表明撞击产生的不稳定波导致了液膜的破碎，且只有在射流超过临界韦伯数的时候才会出现，与雷诺数无关。Lai等[3]试验研究了流体的物理性质对双股撞击雾化特性的影响，通过改变流体粘度和表面张力得到了多达10种的喷雾模式。张蒙正等[4-5]用激光全息及图像处理技术研究了双股撞击式喷雾的撞击夹角、孔径比和动量比变化对雾化性能的影响，并通过对实验数据的分析整理获得了索特尔平均直径的经验公式。邓寒玉等[6]实验分析了射流自由长度对凝胶推进剂撞击雾化的影响，结果表明,根据射流速度合理选取自由长度可以获得更好的雾化效果。刘晓伟等[7]研究了鲁泊数和孔径比对直撞击式喷注器性能的影响，试验表明兼顾两者才能使氧化剂和燃料达到最佳混合效果，提高燃烧效率。

近年来，雾化的数值模拟技术发展很快。与实验研究相比，数值模拟能够获取雾化过程的更多细节，可以与实验结果相互补充互相验证，有助于更加深入地研究雾化机理。Inoue Chihiro等[8]运用CIP-LSM方法模拟了双股射流撞击雾化，发现液膜的动态特性对下游的液丝和液滴分布有重要影响。Ma Dongjun等[9]利用VOF方法结合AMR技术，对射流撞击雾化形式和液膜破碎等现象进行了数值模拟。郑刚等[10]基于CLSVOF方法对双股互击式喷嘴雾化进行了数值模拟，并详细考察了动量比对液膜特性的影响。李佳楠等[11]基于开源程序Gerris完成了撞击式喷注单元雾化过程的仿真模拟，与试验数据进行对比，验证了计算的有效性，给出了数值求解精度。但是，雾化过程的数值模拟往往涉及多相、多尺度流动问题，需要处理大变形、自有界面问题，因此计算量很大。

无网格粒子法是一种全Lagrange方法，在处理具有大变形、自由面等问题的时候，具有网格法无法比拟的巨大优势。强洪夫等[12-13]将SPH方法探索性地应用于射流撞击形成液膜和凝胶推进剂一次雾化仿真研究，解决了传统网格法难以解决的自由面、大变形等问题，模拟结果与实验结论基本一致。韩亚伟等[14]运用SPH方法对双股液体射流撞击雾化问题进行了三维数值模拟。勾文进等[15]将MPS方法应用于直流撞击式喷嘴雾化模拟，成功模拟了雾化的三个模态，但受限于MPS方法较大的计算量，缺乏定量分析。国内还未见将MPS方法应用于双股射流撞击雾化孔径比和动量比的分析相关文献。

为解决MPS方法计算量大的问题，可以将GPU并行加速技术应用于MPS方法。GPU是一种新的可应用于大规模并行计算的处理器和计算机集群的计算架构，最初主要作为游戏行业中的图形计算处理器，随着统一计算设备架构(Compute Unified Device Architecture，CUDA)的发布，GPU在并行计算中有着巨大优势，被越来越多地应用于大规模科学计算。基于GPU的高性能计算主要采用异构架构，即CPU+GPU模式。计算过程中使用CPU执行串行工作，控制主程序的复杂流程，将需要批量处理的向量数据传输给GPU存储器，由GPU的众多处理器执行快速的并行计算。目前在国内公开发表资料中，采用GPU异构并行技术优化加速MPS方法的研究总体较少。

本文基于CUDA开发异构并行加速MPS雾化程序，实现了双股射流撞击雾化模拟。通过对典型工况下的雾化现象进行模拟，分析了孔径比和动量比对雾化特性的影响规律。

1 方法

1.1 MPS方法控制方程与离散

MPS方法是一种完全拉格朗日粒子方法，界面始终清晰，不需要传统网格方法在模拟过程中存在的界面追踪或捕捉，在自由面模拟和大变形流动的模拟方面有自己的优势。

MPS方法中，不可压缩流体的控制方程为

▽·u=0

(1)

(2)

式中ρ为流体的密度；u为速度矢量；t为时间；F为体积力；p为压力；ν为运动粘度。

MPS方法基于核函数对控制方程进行离散，其方程为

(3)

式中re为核函数影响域；r为两个粒子之间的距离。

粒子数值密度为

(4)

式中rj和ri分别为粒子j和粒子i的坐标。

MPS方法采用梯度算子模型与拉普拉斯算子模型离散控制方程。梯度算子模型为

(5)

式中d为空间维数；n0为初始粒子数密度；φi为粒子i的物理量；φj为邻居粒子j的物理量。

拉普拉斯算子模型为

(6)

其中

(7)

MPS方法采用了SMAC算法对控制方程进行求解。其压力泊松方程PPE(Pressure Poisson Equation)为

(8)

式中n*为显式阶段粒子移动后的粒子数密度；Δt为时间步长；pn+1为下一时间步压力值。

压力求解后，速度修正量为

(9)

最后更新速度和位置：

(10)

(11)

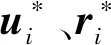
本文在进行显式计算时，加入表面张力的计算。本文采用一种基于自由能的表面张力模拟[16]，该模型非常易于应用到MPS中。

1.2 GPU并行加速

利用所述的梯度模型和拉普拉斯模型将流体的控制方程离散并求解，求解流程如图1所示。

图1 GPU加速MPS方法流程图

粒子法虽然能够较容易地模拟自由面和大变形流动等问题，但是计算量太大。一方面，不同于基于欧拉观点的网格方法，MPS计算过程中粒子自由移动，每个时间步需要对领域粒子进行检索；另一方面，不同于显式的SPH方法，MPS方法需要求解大型稀疏矩阵。这两部分在MPS方法的求解过程中占据时间较长，同时也是程序并行的难点。本文采用Simon[17]提出的Link-list算法实现领域粒子的搜索，该方法不仅可以高效搜索领域粒子，而且优化了后续步骤在GPU内存上的使用效率。为最大限度的发挥GPU的优势，在程序开发时遵循了包括最小化GPU-CPU数据传输、最小化warp内线程分支、优化显存访问模式以及多使用共享显存等原则。为减少设备端主机端数据传输，所有计算均在GPU上执行，数据只有需要保存时才会被传输到主机端。

GPU加速程序在典型算例中，最大加速比为16，取得了较好的加速效果[18]。

2 结果与讨论

2.1 计算模型

根据直流撞击式雾化试验，本文数值模拟如图2所示，夹角为2θ的两股射流位于XOY平面，以初始速度V沿各自轴线方向运动，在撞击点O处发生撞击，进而在YOZ平面形成液膜、液丝和液滴。

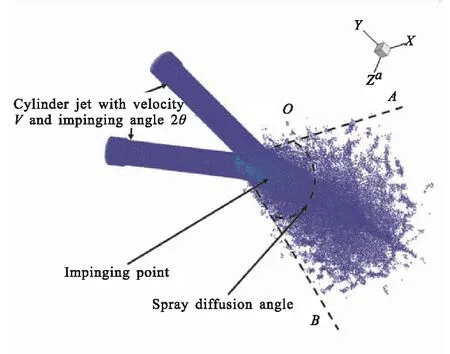
图2 双股射流撞击雾化计算模型

本文计算中涉及的物性参数主要有密度、粘性系数以及表面张力系数等，如表1所示。

液滴的索特尔平均直径(Sauter Mean Diameter，SMD)是燃烧流场中常用的性能评价指标[19]。对液滴粒径的统计方法为在某一时刻，统计位于撞击点下游10 mm和20 mm处高度为1 mm的长方体区域内的液滴数目Ni和尺寸Di，如图3所示。根据索特尔平均直径的计算公式：

(12)

表1 物性参数总结

得到该区域内的索特尔平均直径，并近似认为是该平面该时刻的索特尔平均直径。对不同时该平面的索特尔平均直径进行算术平均即认为该平面的索特尔平均直径。液膜破碎长度Lp定义为自撞击点到液丝从液膜上完全剥离时的长度，见图3。

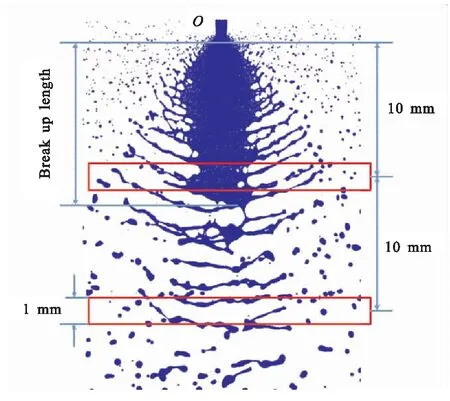
图3 液膜破碎长度和SMD统计方法

喷雾扩散角β定义为垂直于撞击平面内，在撞击点下游以撞击点为顶点的具有一定夹角的雾化区域，如图2所示。

计算模拟了双股射流喷注单元在典型工况下的雾化过程，并与试验数据进行了对比分析。喷嘴的初始直径为1 mm，孔径比为1，动量比为1，撞击夹角为60°，单股射流质量流量为10 g/s，则可计算得到射流速度为12.75 m/s。

如图4所示，计算得到了两股射流撞击形成液膜，液膜在撞击波作用下发生破碎形成液丝，液丝进一步破碎形成液滴的全过程。图4给出了雾场达到稳定状态后的图像与相同条件下的试验结果[11]的对比图，模拟结果与试验结果吻合较好。

2.2 孔径比的影响

孔径比是双股射流撞击式雾化的重要工作参数。实际工程中，由于燃料与氧化剂的密度不同，当要求同时满足推进剂最佳混合效果以及燃烧效率的时候，会将燃料孔与氧化剂孔设计成不同的大小，即双股射流孔径比不为1。本文模拟了一系列不同孔径比的双股射流撞击雾化过程。撞击夹角均为60°，射流的动量比为1，射流孔的尺寸、孔径比以及射流的质量流量之比如表2所示。

图4 雾场模拟和试验对比图

表2 射流孔尺寸、孔径比和射流质量流量

孔径比为1.6时的正面雾场图片如图5所示，与相同条件下的试验拍摄的雾场[11]结构一致：都观察到了雾场存在明显的偏斜；射流孔径比越大，雾场的偏斜程度就越大；液膜的形状是凹形的，有将孔径较小的射流包围的趋势。

图5 孔径比为1.6时模拟结果与试验结果对比

由表2可知，孔径较小的射流速度较大，撞击时的穿透能力较强。虽然两股射流的喷射动量相同，孔径较大的射流动量没有全部用来与孔径较小的射流发生撞击，实际发生撞击的流体动量是不相同的，这导致了合成射流偏向撞击动量较小的射流，即偏向于孔径较大的射流。孔径较大射流的边缘区域由于未参与撞击沿着射流方向继续运动，因此形成了凹形液膜。

孔径比的变化对喷雾扩散角的影响如图6所示。可见，孔径比的增大会引起喷雾扩散角的增大，但是增大幅度不明显，验证了文献[4]的试验结论。

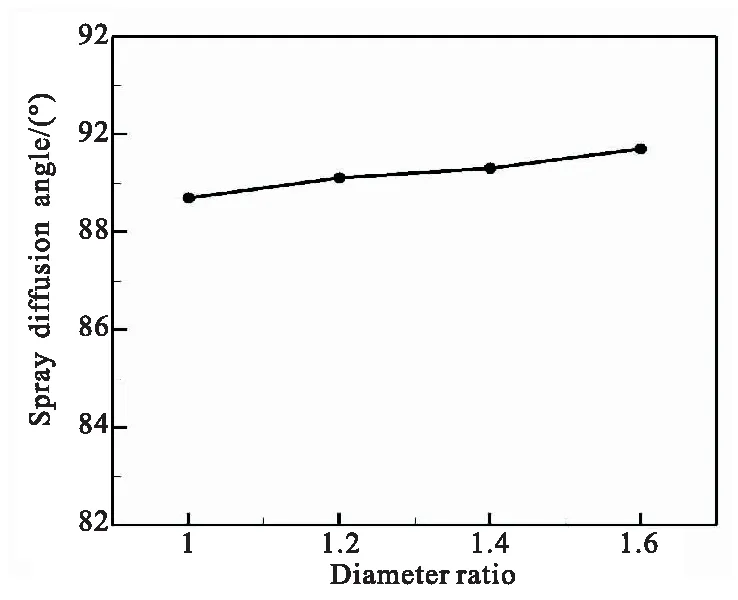
图6 不同孔径比下喷雾扩散角的变化

由图7可知液膜破碎长度随孔径比的增大而增大，而且在大孔径比的时候增加较快，这是因为孔径加大，大孔径射流没有参与撞击的部分增加，参与撞击的射流的相对动量减小，造成了不充分的雾化，因此液膜会在更长的距离内达到破碎临界点。

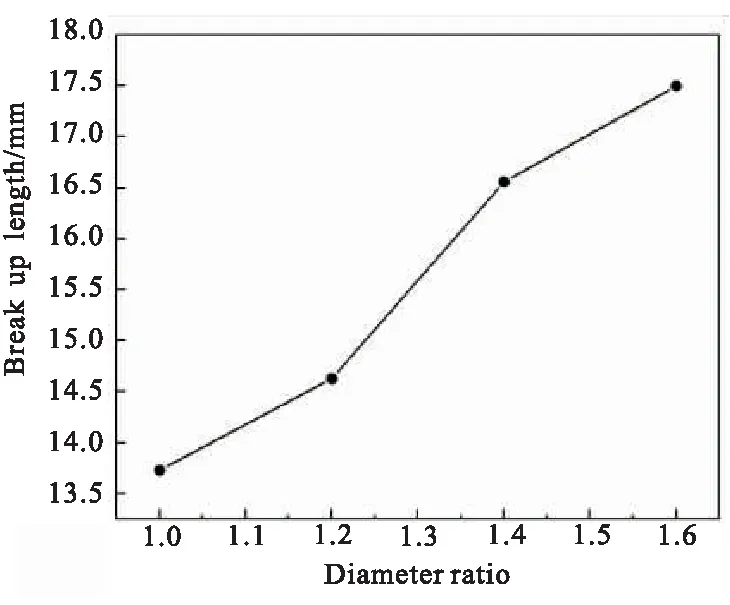
图7 不同孔径比下液膜破碎长度的变化

对不同孔径比的雾化液滴的索特尔平均直径进行了统计，结果见图8，随着孔径比的增加，雾化场的索特尔平均直径也会增加。射流孔径比对液滴尺寸的影响是正变的，这与文献[20-21]结论一致。

由以上分析可知，孔径比的增加将会导致两股射流混合的不均匀，同时也导致了雾化变差。因此，考虑双股射流撞击式雾化的时候，孔径比取值不宜过高。

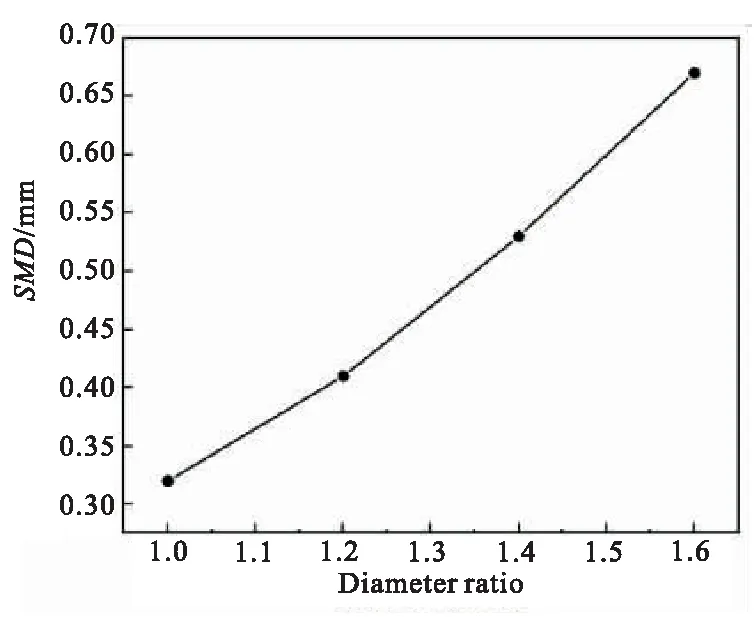
图8 不同孔径比下SMD的变化

2.3 动量比的影响

动量比也是双股射流撞击式雾化的重要工作参数。当孔径比为1时，在实际工程中，为满足需要的混合比时，由于燃料与氧化剂的密度以及射流速度的差异，两股射流的动量比可能不为1。因此，本文模拟了一系列不同动量比的雾化过程，研究不同动量比对雾化结果的影响。计算中，撞击夹角为60°，射流孔直径为1 mm且孔径比为1，射流动量比以及射流质量流量之比如表3所示。

表3 射流动量比和射流质量流量统计

动量比为1.5、1.75和2.0时雾场的正面模拟结果图像分别如图9(a)～(c)所示。图9的雾场模拟结果与相同条件下文献[11]试验拍摄雾场变化趋势一致，都观察到了雾场向动量较小的一侧出现了明显的偏斜。且随着动量比的增加，偏斜程度有所增加。雾场的偏斜角α定义为以液膜和液丝为代表的的雾场主体所在的平面与经过撞击点且与双股射流平面垂直的平面之间的夹角。当动量比为2.0时，模拟得到的偏斜角为21°，根据文献[11]，试验所得的偏转角为24°，模拟得到的偏斜角误差为12.5%。

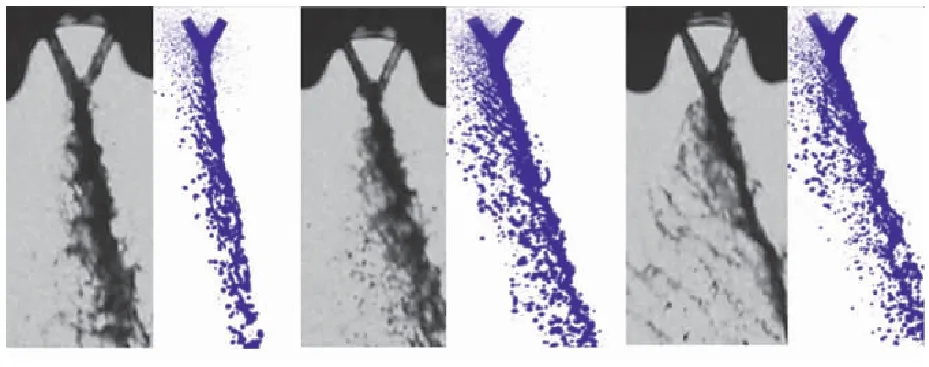
(a)Momentum (b)Momentum (c)Momentum

对模拟得到的雾场偏斜角度进行测量统计，结果如图10所示。可以看到随着动量比的增加，雾场的偏斜程度增大，偏斜角度相应的增大。当动量比由1.5增加到2.0时，雾场的偏斜角度由9°增加到了21°。

动量比的变化对喷雾扩散角的影响如图11所示。随着动量比的增加，喷雾扩散角也会增加，但增加幅度不明显，因此动量比对喷雾扩散角的影响较小，这与文献[4]试验结论一致。

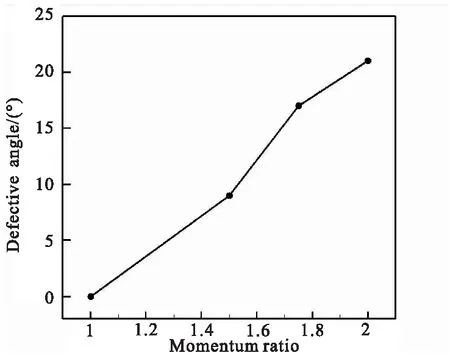
图10 不同动量比下雾场偏斜角的变化

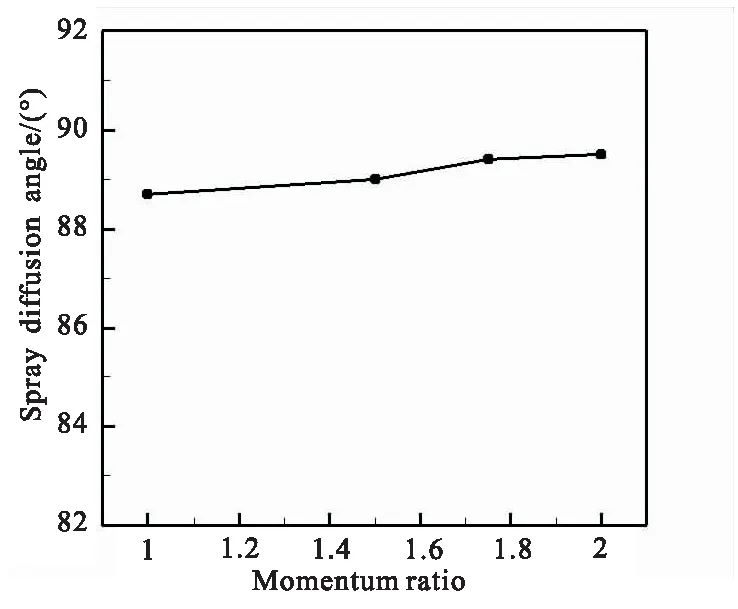
图11 不同动量比下喷雾扩散角的变化

由第2.2节分析可知，孔径比变化的影响实质上是双股射流参与撞击的动量比发生了变化。因此，当孔径比保持不变的时候，随着动量比的增加，未参与撞击部分的动量一直在增加，导致了雾化撞击不充分，雾化结果变差。因此，动量比的增加会导致液膜破碎长度增加，如图12所示。图13统计了不同动量比下的雾化液滴索特尔平均直径。由图可知，雾化液滴的索特尔平均直径随着射流动量比的增加而增加。

图12 不同动量比下液膜破碎长度的变化

图13 不同动量比下SMD的变化

3 结论

本文基于GPU加速的移动粒子半隐式法，对双股射流雾化过程进行了直接数值模拟，成功模拟了液膜变成液丝，液丝破碎成液滴的一次雾化过程。分析模拟结果，得到结论如下：

(1)孔径比通过改变参与撞击的射流动量的变化来影响雾化过程。孔径比不为1的时候，雾场会存在明显的偏斜，同时会形成凹形液膜。

(2)动量比主要影响雾场的偏斜程度，且动量比越大，雾场偏斜程度越大。本文计算中，撞击夹角为60°、孔径比为1时，动量比由1.5提高到2.0，雾场偏斜角由9°提高到21°。

(3)孔径比和动量比的增大都会造成喷雾扩散角的增大，但是变化幅度较小。

(4)孔径比和动量比的增大都会造成雾化撞击不充分，因此液膜会在更长距离内到达临界破碎点，所以使得液膜破碎长度和雾化液滴的索特尔平均直径增大。

后续将进一步改进模拟的精度，对多股射流雾化开展研究，分析各喷注单元之间的干涉关系，并对多股射流雾化进行数值的研究。