弹性环-鱼雷涡轮转子动力学特性分析

张盼盼，史小锋，伊 寅，宋 文

(中国船舶集团有限公司 第705研究所，陕西 西安 710077)

0 引 言

随着高新技术不断地应用，鱼雷正朝着高航速、远航程、大航深、低噪声和精确制导方向发展，有必要研究一种功率近1MW级别的动力推进系统。燃气涡轮机是设计大功率热动力推进系统的最佳选择，由于结构和体积的限制，燃气涡轮机一般采用单级、短叶片、部分进气、冲动式构型，轴承转子是其中重要的组成部件，转子的转速可以达到50 000 r/min[1]。

轴承转子部件的工作环境相对恶劣，当转子主轴高速运转时，它承受着作用于涡轮盘的扭矩，转子重量产生的弯矩和离心力带来的应力等，转子系统设计和制造方面的误差，都会产生重大问题并导致事故发生[2]。包括振动噪声，转子失稳，轴系断裂等，这些事故发生的部分原因是转子系统产生过大的振动。振动过大的原因之一就是转子系统的临界转速设计不合理[3]。

在转子系统结构已经确定的情况下，采用弹性支承能够降低支承刚度，从而降低转子系统的临界转速，最后使转子系统的工作转速远离临界转速并且平稳运行[4]。

常见的弹性支承有弹性环式和鼠笼式，弹性环结构简单，重量轻，占用空间较小[5]，且具有良好的刚度特性，调整弹性环的结构参数就可以改变支承刚度来调节转子的临界转速，所以分析弹性环的刚度特性是非常重要的环节[6]。

曹磊等[7]分别利用解析法和有限元方法研究了弹性环的刚度特性，分析总结了弹性环结构参数对刚度特性的影响；刘勇等[8]利用Ansys参数化语言apdl建立了弹性环的非线性有限元模型，分析结构参数对等效刚度的影响规律，结合实际使用要求，提供了优选的弹性环结构参考方案。解析法计算刚度时精度较低，无法考虑结构参数的影响[9]，本文将基于有限元法对弹性环刚度特性进行研究。

1 刚度分析

1.1 弹性环结构

弹性环属于径向弹性支承，其内外表面有数量相同的凸台，凸台沿着圆周等距交错分布。外凸台跟轴承座的内环面接触，内凸台跟轴承外圈接触，工作状态如图1所示。弹性环的弹性模量为2.11E5 MPa，泊松比为0.3，轴向宽度为16 mm，结构如图2所示，基本设计参数如图3所示，某弹性环结构数据见表1。

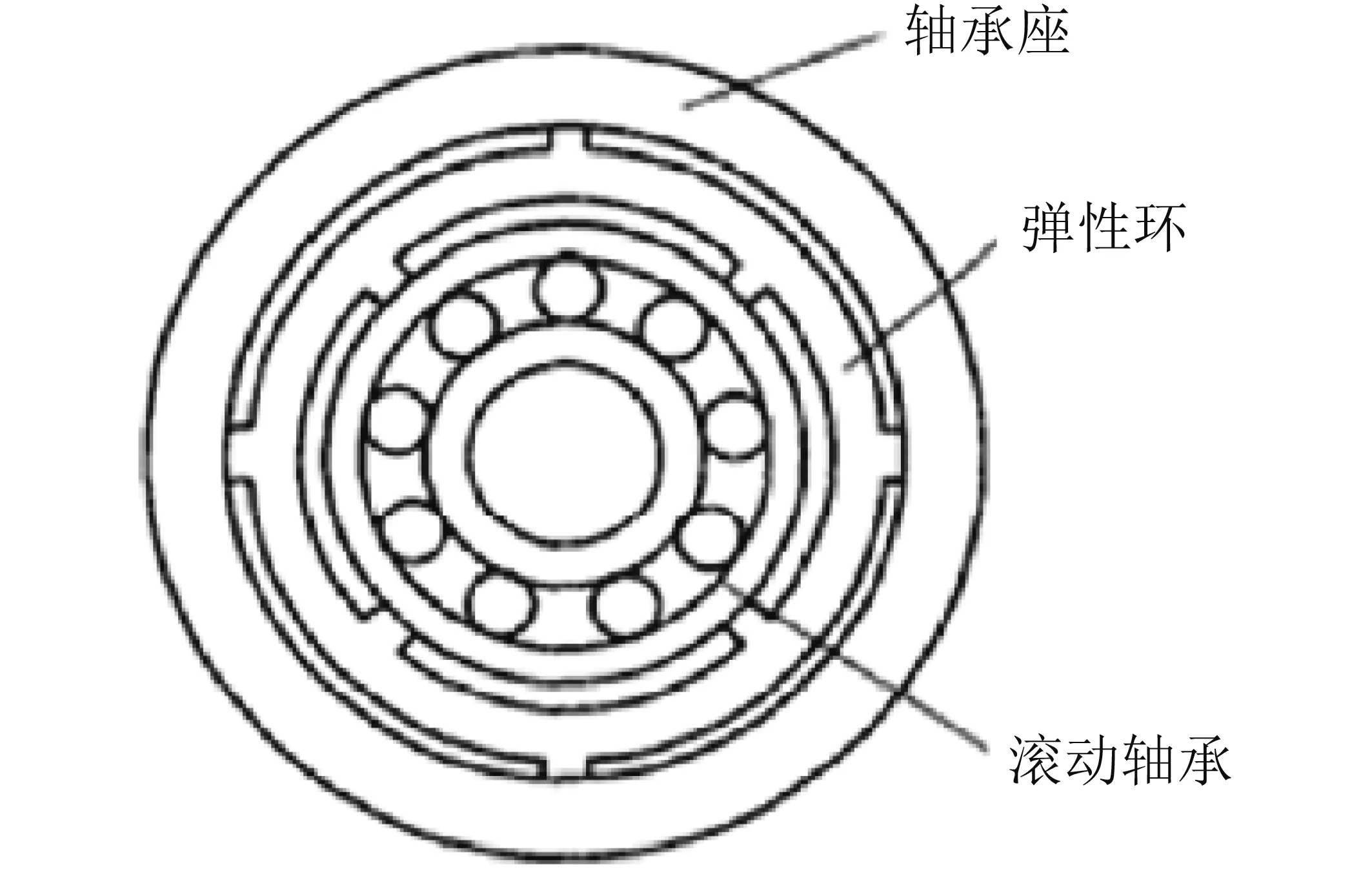
图1 弹性环工作状态示意图Fig.1 Working state diagram of elastic ring

图2 弹性环结构图Fig.2 Structure diagram of elastic ring

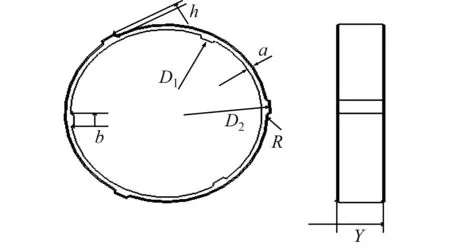
图3 弹性环结构参数示意图Fig.3 Schematic diagram of structural parameters of elastic ring

1.2 有限元模型

弹性环结构是三维弹性固体结构，依据结构形式及受力特点，三维弹性固体受力问题可简化为平面应力问题、平面应变问题或轴对称问题，这些特殊形式弹性固体问题仍属于弹性力学研究范畴。

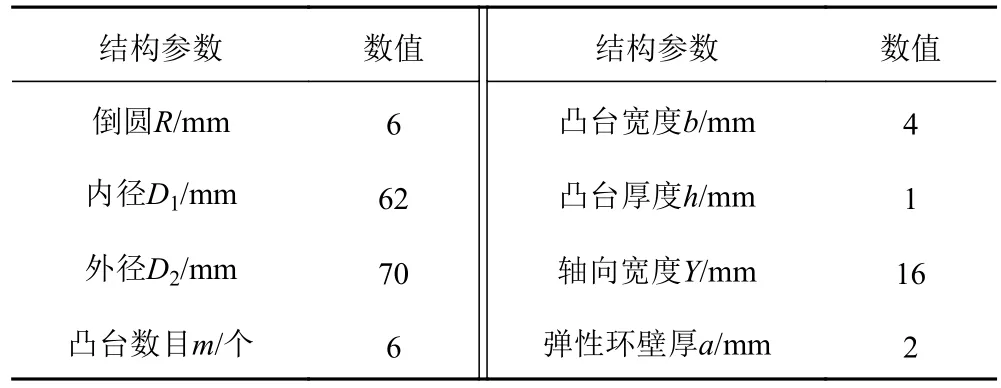
表1 弹性环主要结构参数Tab.1 Main structural parameters of elastic ring

在弹性环刚度计算中：

1）x与y向的尺寸远远大于z向；

2）受力方向为径向；

3）受力均匀分布在凸台周边。

由于弹性环结构的特殊性，可以将其简化为平面应力问题进行处理，进行刚度特性分析。文献[6]中的计算结果表明，凸台倒圆角R对弹性环刚度计算结果影响不大，为了编写程序简便，此变量忽略不计。弹性环的内径D1，外径D2，轴向宽度Y为固定参数，凸台数目m，凸台宽度b，凸台厚度h为设计变量。通过改变以上3个设计变量就可以调节弹性环的刚度，采用控制变量法研究弹性环的结构参数对其刚度变化的影响规律，借此揭示弹性环的刚度特性，为进一步研究转子系统中弹性环刚度变化对转子动力学特性的影响规律奠定基础。

将弹性环简化为平面应力问题来研究弹性环刚度特性，首先对弹性环截面进行网格划分，进行有限元建模。弹性环网格图如图4所示，依据有限元法的基本原理编写相应求解程序，计算求得弹性环的刚度。

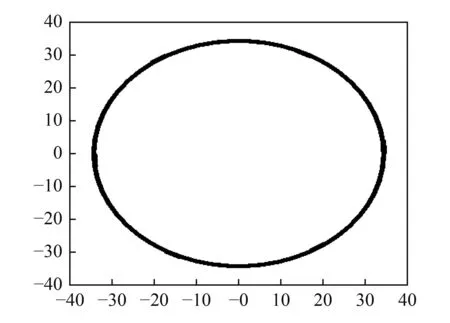
图4 弹性环网格图Fig.4 Mesh graph of elastic ring

1.3 分析结果

采用径向力加载形式，对内凸台处的某个节点加载径向力，通过有限元静力分析求解得到该节点处的径向位移，利用刚度计算式（1）得到弹性环不同节点位置的刚度值。由于弹性环是周向对称结构，故计算弹性环在一个周期内不同位置处的刚度值，取其平均值作为弹性环的刚度，弹性环结构参数为表1时，计算得到弹性环的刚度值为4.3939E+05 N/m，计算数据见表2。

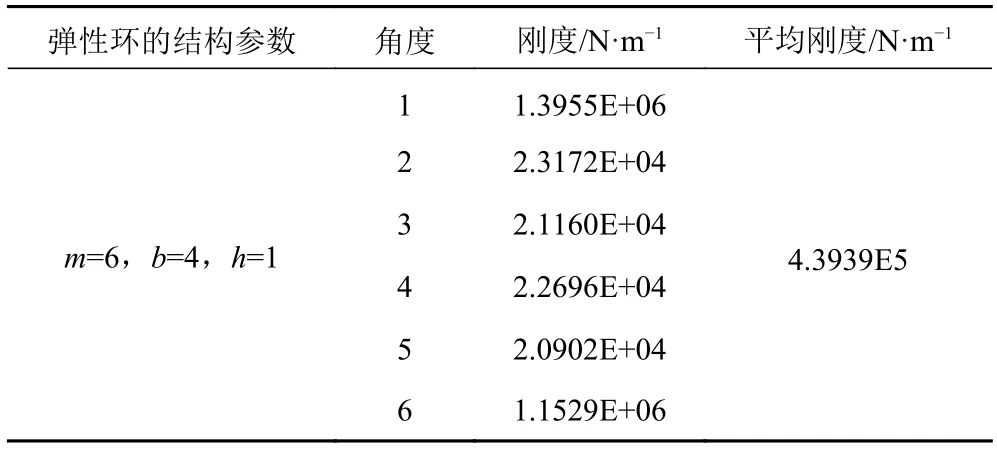
表2 弹性环刚度值Tab.2 Elastic ring stiffness value

式中：k为结构的静刚度，F为加载径向力，S为径向位移。

1.4 验证模型

以文献[6]中的算例为模型验证本文弹性环刚度计算方法的可靠性。文献[6]中弹性环的基本设计参数为：内、外凸台数m=8，弹性环宽度Y=15 mm，内径D1=65 mm，外径D2=68 mm，壁厚h=1 mm，倒圆R=10 mm，凸台宽度b=5 mm，该弹性环使用的材料为1Cr11Ni2 W2MoA，弹性模量为1.96E5 MPa，泊松比为0.3。本文计算所得的刚度值和文献[6]数据对比见表3。

表3 弹性环刚度计算结果对比（N/m）Tab.3 Elastic ring stiffness value（N/m）

通过模型验证表明本文将弹性环简化为平面应力问题来计算弹性环刚度是一种可行的方法。本文所用方法的精度高于传统的近似解析法，在弹性环刚度的计算过程中，可以把弹性环的结构参数化，方便后续分析弹性环的凸台数目、凸台宽度、凸台厚度等结构参数对弹性环刚度的影响。

2 结构参数对刚度的影响研究

当弹性环的内径D1，外径D2，轴向宽度Y为固定参数，弹性环的刚度由凸台数目m，凸台宽度b，凸台厚度h决定。本文研究中弹性环结构有3个可变参数，凸台宽度b取4，5，6，7，凸台数目m取6，8，10，12，14，凸台厚度h取 0.5，0.6，0.7，0.8，0.9，1，为了分析每个变量对刚度的影响规律，采用控制变量法进行研究。结合上述有限元静力分析的方法，进行弹性环结构参数对刚度的影响规律研究。

2.1 刚度随涡动角的变化规律

弹性环是周向对称结构，当转子系统稳态运转时，内外凸台受到的力是周期性变化的，相邻内外凸台之间为1个周期，弹性环的刚度值随涡动角的改变而改变。分别计算3个不同结构参数的弹性环在1个周期内的刚度值，1个周期内刚度的平均值可以作为弹性环的平均刚度，计算结果见表4。

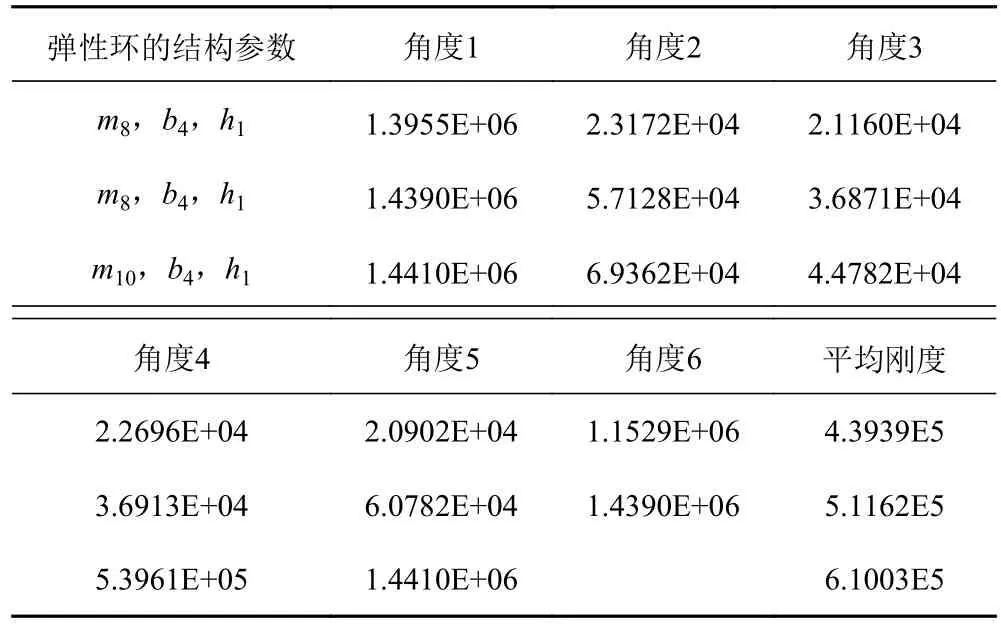
表4 弹性环刚度值（N/m）Tab.4 Elastic ring stiffness value（N/m）

2.2 刚度随凸台数目的变化规律

其他结构参数不变，改变凸台数目m，得到弹性环的刚度随凸台数目的变化曲线，如图5所示。取h=1，当凸台宽度b分别为4，5，6，7时，凸台数目m分别取6，8，10，12，14。通过对不同结构弹性环进行有限元静力分析，得到4组弹性环刚度随凸台数目m变化的曲线，如图6所示。

图5 弹性环刚度随凸台数目的变化规律Fig.5 The change law of elastic ring stiffness with number of bosses

通过对图5和图6进行分析表明，弹性环的刚度随凸台数目m的增大而增大，这是因为弹性环中的每一个环段可以看做两端固支的梁段，中间受到集中力的作用，当凸台数目m越大时，环段也越短，其承载力越高，所以弹性环的刚度值越大。而且弹性环的凸台数目越大，刚度值的增大速度越快，两者之间有着复杂的非线性关系。

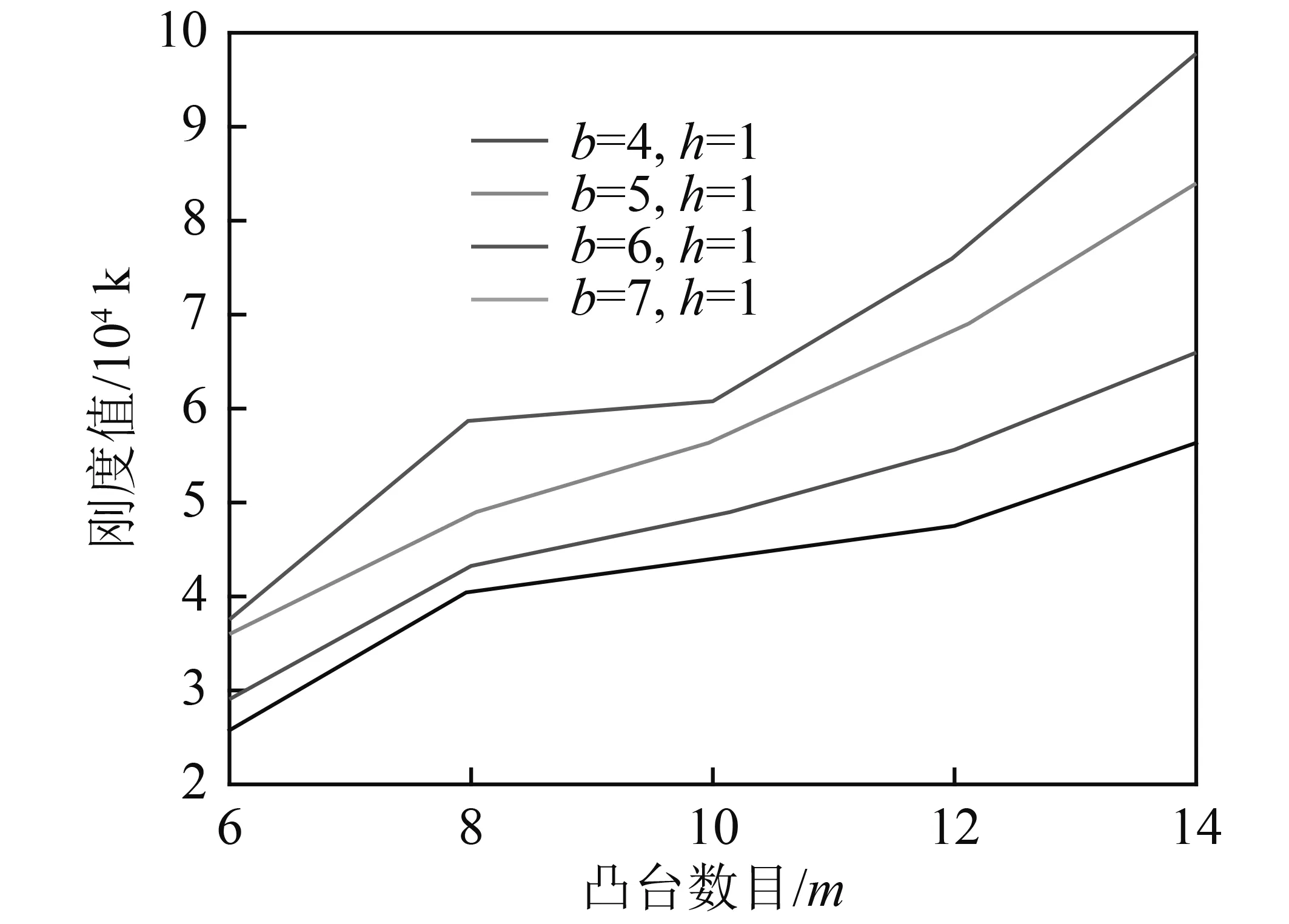
图6 弹性环某一节点刚度值随凸台数目和凸台宽度的变化规律Fig.6 Variation of stiffness of a joint of elastic ring with the number and width of boss

2.3 刚度随凸台宽度的变化规律

其他结构参数不变，改变凸台宽度b，得到弹性环的刚度随凸台宽度的变化曲线，如图7所示。取h=1，当凸台数目m分别为6，8，10，12，14时，凸台宽度b分别取4，5，6，7。通过对不同结构弹性环进行有限元静力分析，得到5组弹性环刚度随凸台宽度b变化的曲线，如图8所示。

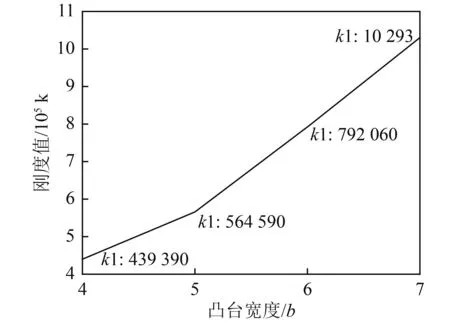
图7 弹性环刚度随凸台宽度的变化规律Fig.7 The variation law of elastic ring stiffness with boss width

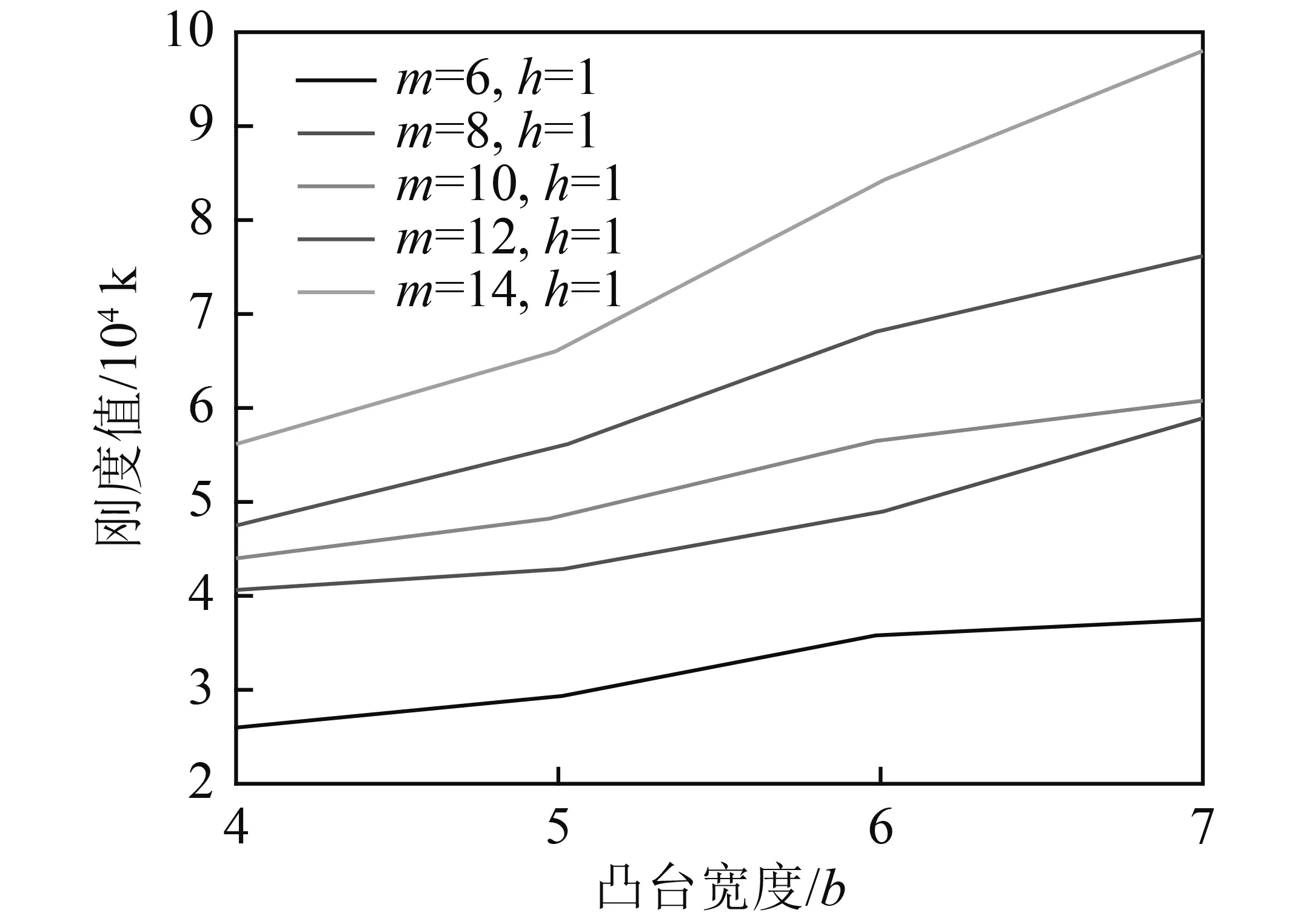
图8 弹性环某一节点刚度值随凸台数目和凸台宽度的变化规律Fig.8 Variation of stiffness of a joint of elastic ring with the number and width of boss

通过对图7和图8进行分析表明，弹性环的刚度值随凸台宽度的增大而增大，这是因为凸台宽度增大，相当于弹性环每一环段的凸台宽度占每一环段的比例增大，所以会导致弹性环的刚度增大，弹性环刚度增加趋势接近线性变化。

2.4 刚度随凸台厚度的变化规律

其他结构参数不变，改变凸台厚度h，得到弹性环的刚度随凸台厚度的变化曲线。取凸台数目为8，凸台宽度为4，凸台厚度h分别取0.5，0.6，0.7，0.8，0.9，1。通过对不同结构弹性环进行有限元静力分析，得到弹性环刚度随凸台厚度h变化的曲线如图9所 示。

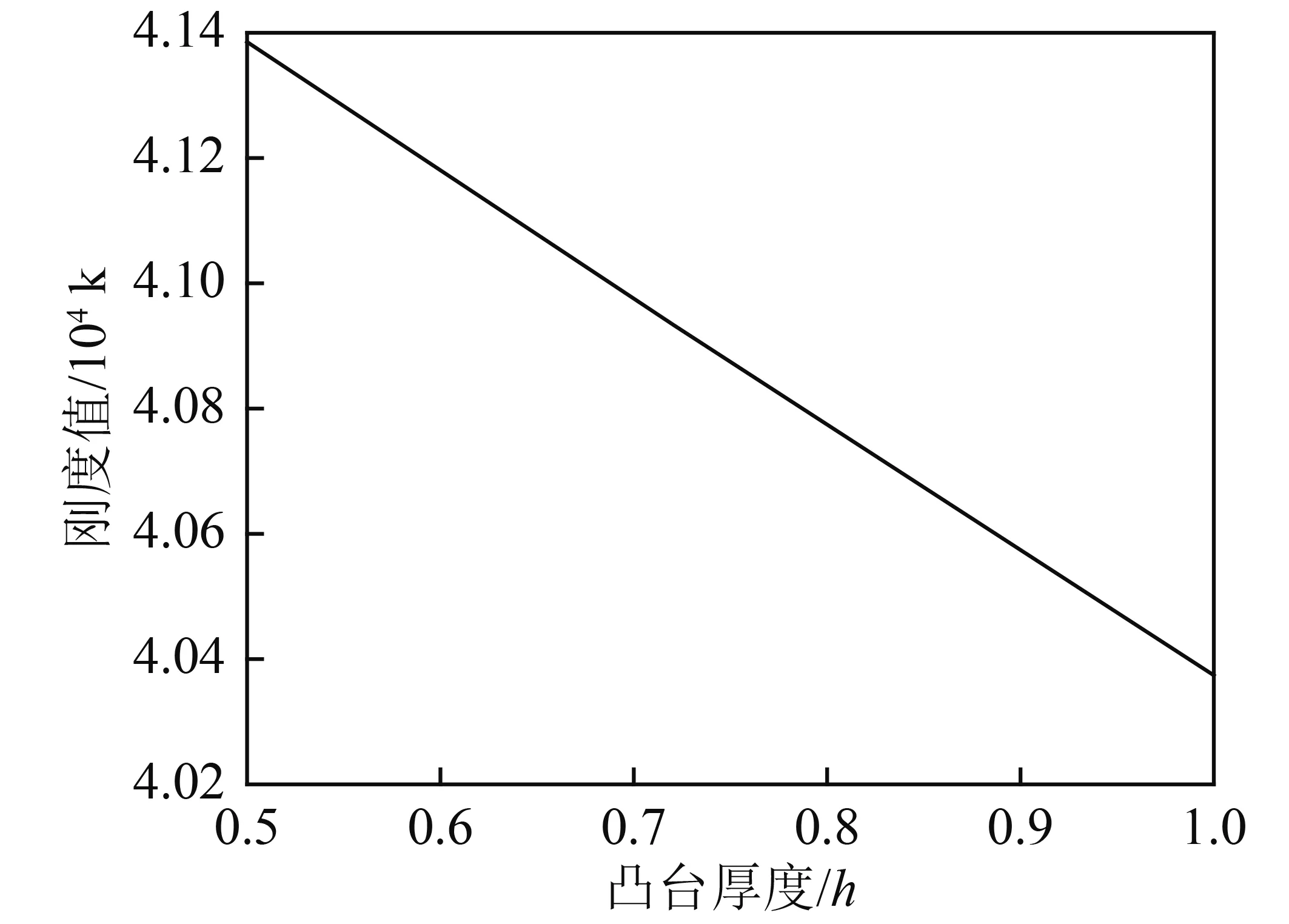
图9 弹性环某一节点刚度随凸台厚度的变化规律Fig.9 Variation of stiffness of a joint of elastic ring with the thickness of boss

通过分析图9可以看出，随着弹性环凸台厚度h的增大，弹性环的刚度随之减小，刚度减小的幅度不是很大，并且近似于线性变化。

2.5 刚度随参数变化的三维图

本文弹性环的结构参数有3个可变参数，从以上3个参数对弹性环刚度值的影响规律可以看出，随着凸台厚度h的增大，弹性环的刚度随之减小，但是相比较凸台数目m和凸台宽度b这2个参数，弹性环刚度变化随凸台厚度h的幅度可以忽略，故在弹性环结构优选设计中，只考虑凸台数目和凸台宽度这2个参数。当凸台厚度h=1 mm时，弹性环的刚度随凸台数目和凸台宽度变化的三维图如图10所示。

3 支承刚度对临界转速的影响

本文的转子系统是两支点支承的悬臂转子，在转子系统的结构构型已经确定的情况下，支承对转子系统动力学特性有重要的影响，从以往研究中发现，计算转子系统的临界转速主要有2种方法：传递矩阵法和有限元法。传递矩阵法程序设计简单、占用内存小，适用于链式结构系统[10]，所以本文采用传递矩阵法计算转子系统的临界转速，进一步分析支承刚度对临界转速的影响规律。

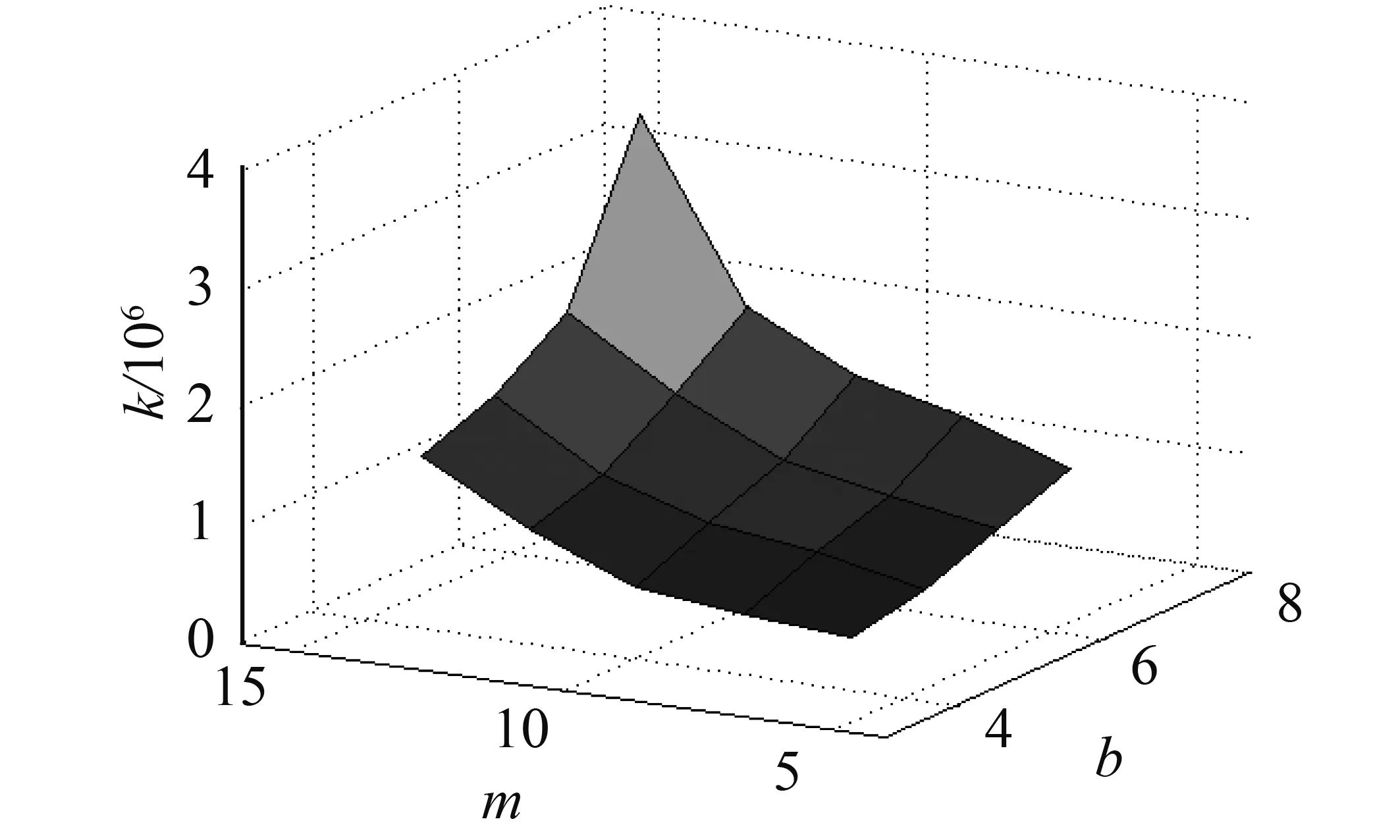
图10 弹性环平均刚度变化三维图Fig.10 Three dimensional diagram of average stiffness change of elastic ring

3.1 临界转速计算

燃气涡轮机转子系统主要由涡轮盘、主轴、输出轴、花键和深沟球轴承组成。属于单盘悬臂转子系统，燃气涡轮机转子系统结构见图11。

图11 燃气轮机转子系统Fig.11 Gas turbine rotor system

依据传递矩阵法的分段原则将该燃气涡轮机转子系统分成13段有质量的均质轴段，1个涡轮盘，4个弹性支承，简化之后得到转子动力学模型，如图12所示。图中从左向右第1个和第2个弹性支承依次命名为前支承和后支承。

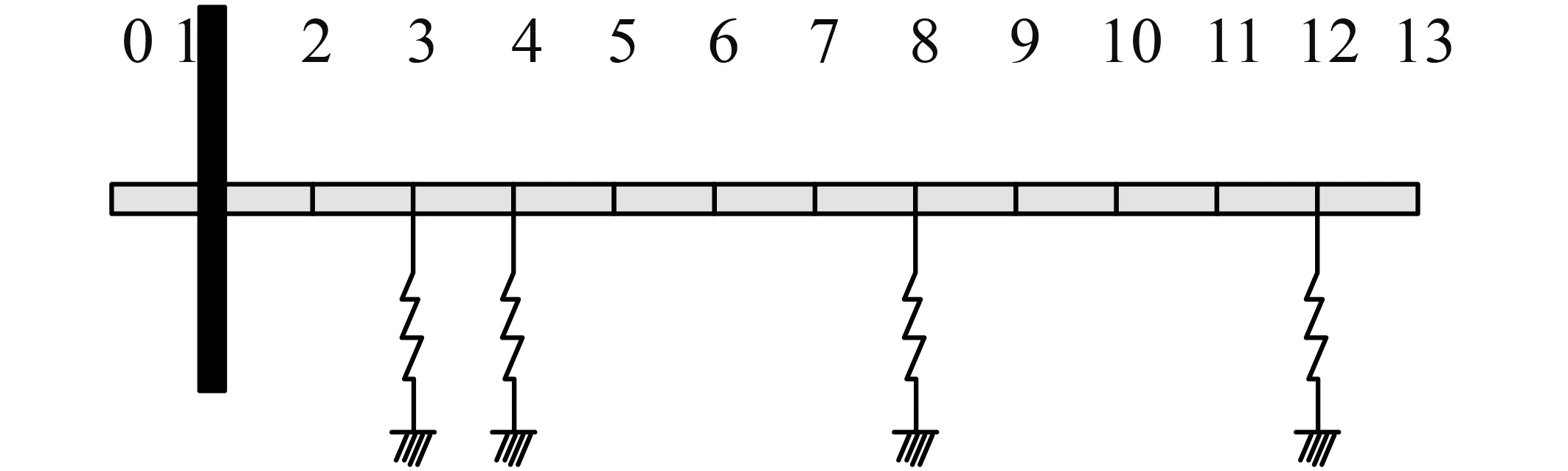
图12 燃气轮机转子系统动力学模型Fig.12 Dynamic model of gas turbine rotor system

利用传递矩阵法计算转子系统的临界转速，通过Riccati传递矩阵法得到剩余量曲线，如图13所示，从图中可以得到前3阶临界转速。

曲线与纵坐标零点的交点对应的转速就是转子系统临界转速。从图13得知，1阶临界转速为2 585 rad/s，2 阶临界转速为 13 291 rad/s，3 阶临界转速为 16 983 rad/s。临界转速与转子系统的质量分布和弹性支承有关系，工程上主要看前3阶临界转速。

3.2 支承刚度对临界转速的影响

3.2.1 临界转速随前支承刚度的变化规律

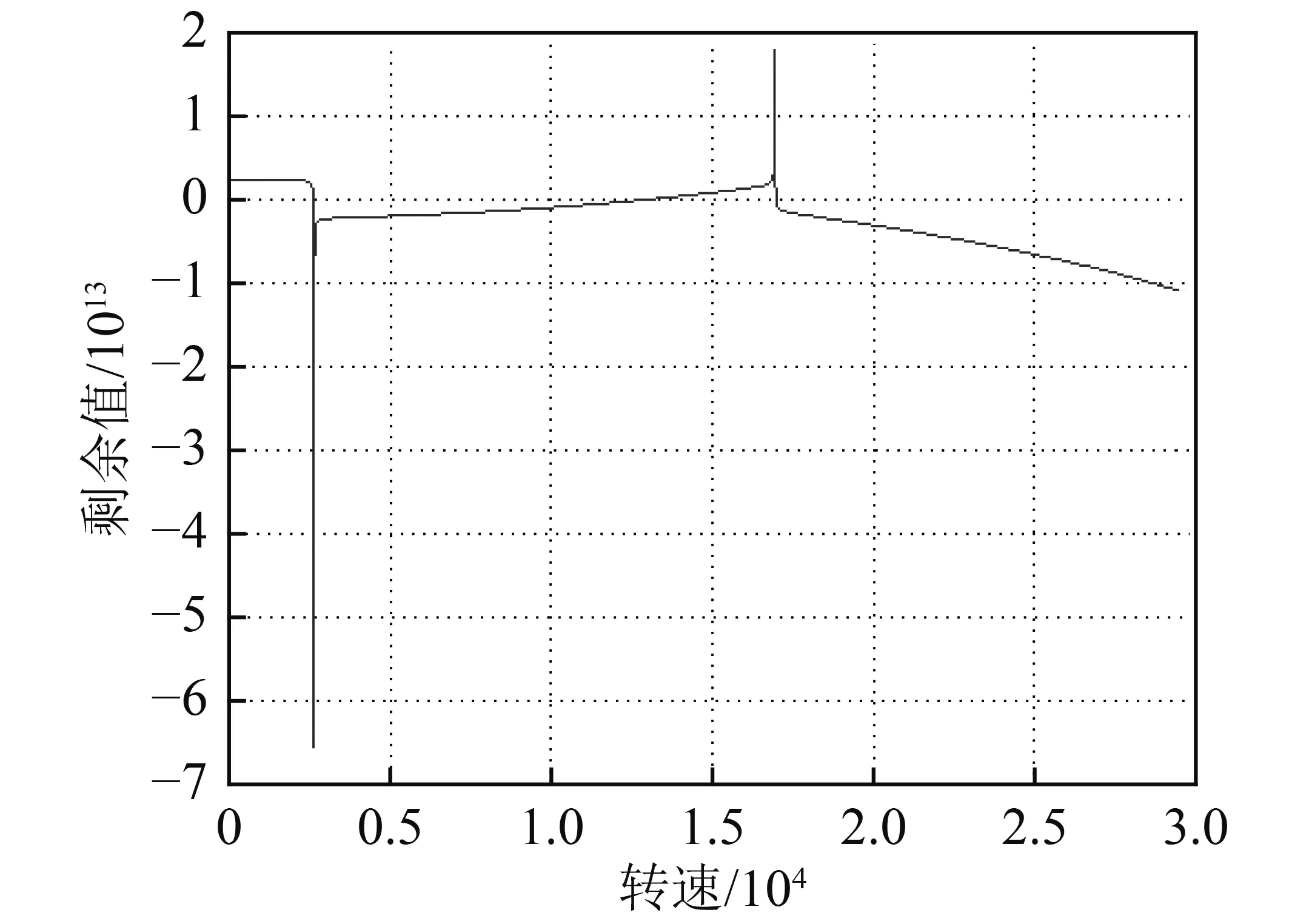
图13 临界转速-剩余量曲线Fig.13 Critical speed residual curve

改变前弹性支承的刚度，变化范围为1E5～5E7 N/m，通过计算得到燃气涡轮机转子系统前3阶临界转速随前弹性支承刚度变化的曲线如图14所示。

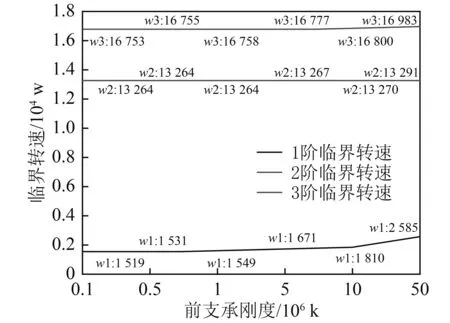
图14 临界转速随前支承刚度的变化Fig.14 Change of critical speed with front support stiffness

从图14可以看出，改变前弹性支承的支承刚度，3阶临界转速均有增大，第1阶增大的幅度大于第2阶和第3阶，第2阶和第3阶临界转速几乎没有太大的变化，前3阶临界转速的变化率见表5。

表5 前3阶临界转速的变化率/%Tab.5 Change rate of the first three critical speeds

3.2.2 临界转速随后支承刚度的变化规律

改变后弹性支承的刚度，变化范围为1E5～5E7 N/m，通过计算得到燃气涡轮机转子系统前3阶临界转速随后弹性支承刚度变化的曲线如图15所示。

由图15可知，随着后支承刚度增大，转子系统的临界转速均增大，但是第1阶、第2阶和第3阶临界转速增大的幅度都不是很大，所以后支承刚度对转子系统的动力学特性没有显著的影响，前3阶临界转速的变化率见表6。

3.3 前后弹性环参数对临界转速的影响

通过以上分析可以看出：前弹性支承的刚度变化对转子系统的第1阶临界转速影响较大，对第2阶和第3阶临界转速的影响几乎为0；后弹性支承的刚度变化对转子系统的前3阶临界转速的影响很小，在弹性环结构优化设计时可以不用考虑后弹性环支承结构参数的改变。

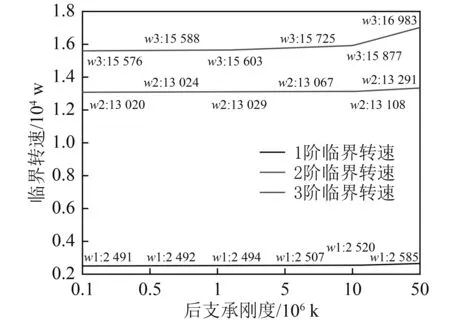
图15 临界转速随后支承刚度的变化Fig.15 Change of critical speed with rear support stiffness

表6 前3阶临界转速的变化率/%Tab.6 Change rate of the first three critical speeds

综上所述，转子系统的第1阶临界转速随着前弹性环参数的改变而改变，第2阶和第3阶临界转速几乎不受弹性环参数变化的影响。本文燃气涡轮机转子的转速可达到50 000 r/min，所以仅考虑弹性环结构参数变化对转子系统第1阶临界转速的影响，表7为前支承处弹性环结构参数变化对第1阶临界转速的影响。

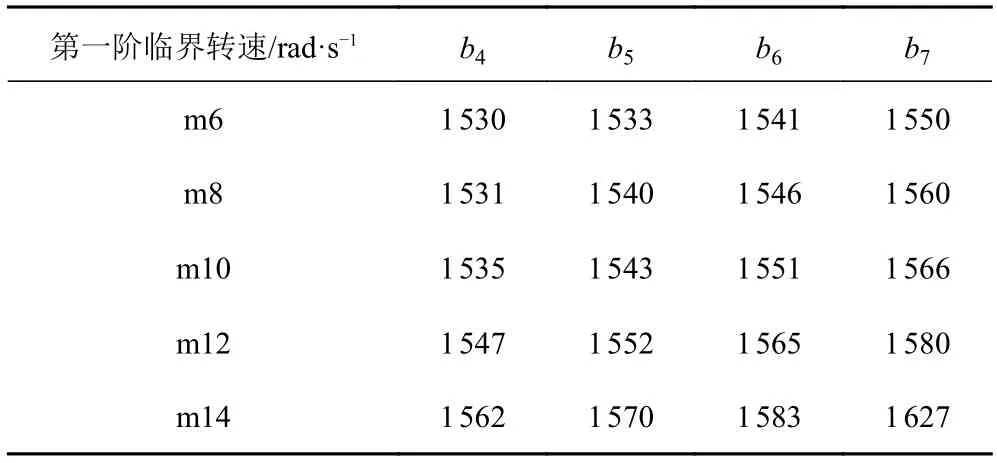
表7 第1阶临界转速随前弹性环参数的变化Tab.7 The change of the first critical speed with the parameters of the front elastic ring

4 结 语

将弹性环刚度特性问题简化为平面应力问题，结合有限元方法编程对其刚度特性进行分析，研究弹性环的凸台数目、凸台宽度以及凸台厚度对其刚度特性的影响。弹性环刚度随着凸台数目增大而增大，凸台数目越多，弹性环刚度的增大速度越快，弹性环刚度与凸台数目之间是一种较为复杂的非线性关系。随着弹性环宽度的增大，弹性环的刚度也随之增大，并且近似于线性变化。随着弹性环凸台厚度的增大，弹性环的刚度随之减小，刚度减小的幅度不是很大，近似于线性变化。

转子系统的第1阶临界转速随着前支承处弹性环结构参数的改变而改变，第2阶和第3阶临界转速几乎不受弹性环结构参数变化的影响。可以通过调整前支承处弹性环结构参数来改变转子系统的第1阶临界转速，给出不同弹性环结构参数时转子系统的第1阶临界转速，对弹性环结构的选优具有一定的指导意义。