支撑架顶部构造对其承载力的影响分析
索小永,金华超
(1.安徽工程大学 建筑工程学院,安徽 芜湖 241000;2.开封市天开市政园林工程有限公司 工程部,河南 开封 475000)
扣件式支撑架是工程中常用的临时结构,其中,《建筑施工模板安全技术规范》JGJ 162-2008,《建筑施工扣件式钢管脚手架安全技术规范》JGJ 130-2011,《混凝土结构工程施工规范》GB 50666-2011,《建筑施工临时支撑结构技术规范》JGJ 300-2013,《建筑施工脚手架安全技术统一标准》GB 51210-2016等多本规范标准对其搭设构造、承载力计算有明确要求,但各本规范之间构造搭设不统一、不协调。例如竖向剪刀撑设置间距,水平剪刀撑间距各本规范要求不一,另支撑架顶部水平杆步距加密构造称为加强层,有些规范并未要求设置。虽有学者进行了支撑架的缺陷对其承载力影响的研究,但加强层设置对承载力影响的研究较少。亦有学者根据施工现场支撑架搭设情况,对其承载力进行分析,但其研究的现场搭设的支撑架未设置加强层。加强层虽是构造,但搭设过程中存在漏设或设置不合理情况,反映出工程技术人员对其作用认识不充分。以加强层设置情况不同,对支撑架承载力的影响进行研究,使其作用清楚地展示出来,引起工程技术人员重视。
1 模型建立
根据《危险性较大的分部分项工程安全管理规定》(建办质[2018]31号)文件要求,施工中支撑架搭设高度大于8 m,属于存在重大危险源,需搭设“使用中”标志引起足够警示,其技术方案要进行专家论证。本次建模以高度超8 m支撑架为例进行分析,因实际工程结构高度多变,导致支撑架搭设时,立杆顶部加强层难按标准设置,故本次建模高度为12.5 m、13 m两种情况,以反映加强层设置以后发生的变化。支撑架平面布置图如图1所示。由图1可知,立杆间距0.9 m×0.9 m,步距1.5 m,架体搭设宽度5.4 m×5.4 m,支撑架高宽比均小于2.5,不存在倾覆隐患,竖向剪刀撑沿四周设置,水平剪刀撑设置三道与竖向剪刀撑形成格构柱。高12.5 m的支撑架立面布置情况如图2所示。此高度中支撑架步距均为1.5 m,无加强层如图2a所示,按标准设置加强层如图2b所示。高13 m的支撑架立面布置情况如图3所示。因高度变化,此处顶部加强层不能按照标准设置。钢材采用Q235,弹性模量E
=2.06×10N/mm,钢材强度采用标准值,屈服强度235 N/mm,屈服时应变为0.001 14。为真实反映支撑架边界条件,模型中立杆底部与地面只能传压力,不能传递拉力,受拉退出工作。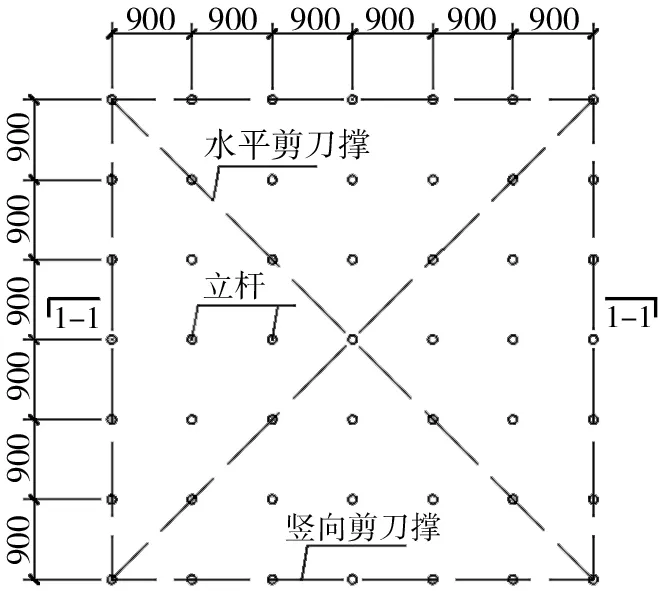
图1 支撑架平面图(单位:mm)

图2 12.5 m高的立面布置图(单位:mm)

图3 13 m高的立面布置图(单位:mm)
2 计算分析
所建立的3个模型均为空间整体模型,分两步进行计算,首先进行屈曲承载力分析,提取第1阶失稳模态,引入100 mm缺陷,然后进行几何、材料双重非线性分析,研究其稳定极限承载能力。这两步主要计算结果如表1所示。由表1可以看出,支撑架一阶屈曲分析,有加强层时,12.5 m和13 m支撑架承载力基本相同,顶部加强间距0.75 m和1.0 m对一阶屈曲承载力影响不明显,但两者均高于无加强层支撑架承载力7.9%。由于一阶屈曲分析对应的是支撑架的理想状态,不考虑缺陷及钢材屈服情况,决定支撑架的承载力上限。为较真实反映支撑架承载力变化情况,应考虑几何、材料双重非线性后的稳定极限承载力,根据表1中计算参数12.5 m高支撑架设置加强层后极限承载力为30.09 kN,比不设加强层承载力25.76 kN提高12.4%,这一结果在工程中不可忽略。12.5 m高支撑架顶部加强层间距0.75 m和13 m高支撑架顶部加强层间距1.0 m,两者极限承载力基本一样,承载力差别4.6%,可认为加强层间距变化对结果影响不大。支撑架失稳破环时立杆顶部竖向沉降位移,基本相等22.5~24.1 mm,而失稳形态中鼓曲侧向位移变化范围较大87.3~101.3 mm,相差15.7%,但无论竖向沉降,还是侧向位移,均超出工程允许偏差范围。

表1 支撑架极限承载力计算结果
表1中有加强层的12.5 m高支撑架和13 m高支撑架最终承载力和变形性能相近,承载力均大于无加强层的12.5 m高支撑架。3个模型支撑架失稳最终形态相近,无加强层12.5 m支撑架失稳形态、有加强层12.5 m支撑架失稳形态、有加强层13 m支撑架失稳形态分别如图4所示。从图4中可以看出,三者均为中部鼓曲而引起的整体失稳,最大鼓曲位置随着顶部加强层设置情况不同而有变化,无加强层最大鼓曲位置靠近上部,加强层设置后使最大鼓曲位置下移,图4a中12.5 m高无加强层支撑架最大鼓曲位置最靠上,图4c中13 m高有加强层(其间距1.0 m)最大鼓曲位置已经下移,图4b中12.5 m高有加强层(其间距0.75 m)最大鼓曲位置最靠下。这是由于顶部设置加强层,加强层所在位置刚度增加,此处抵抗变形能力增强,故使得最大鼓曲位置下移,同样由于加强层的设置使得抗侧移刚度增加后,最终支撑架达到稳定极限承载力时其侧向位移随刚度增加而减小,如表1所示,12.5 m高支撑架无加强层鼓曲最大侧移101.3 mm,设置加强层后,12.5 m高有加强层(其间距0.75 m)最大鼓曲位移87.3 mm,侧向位移减少13.8%,13 m高有加强层(其间距1.0 m)最大鼓曲位移89.2 mm,侧向位移减少11.9%,表明加强层的设置在一定程度改变了支撑架失稳时的力学行为。
进一步研究支撑架随荷载增加其力学行为的变化,为工程监测评判提供依据,提取荷载-变形时间历程如图5所示。由图5a中可以看出,有加强层的12.5 m高支撑架(加强层间距0.75m)和13 m高支撑架(加强层间距1.0 m),两者的侧向鼓曲位移与承载力性能高度接近,加载初期其抗侧刚度明显优于12.5 m高无加强层支撑架。宏观上无论有无加强层,支撑架荷载-侧向位移曲线的力学行为均表现出非线性关系,无加强层的支撑架达到极限承载力时侧向变形大于有加强层支撑架;由图5b中可以看出,有加强层的12.5 m高支撑架(加强层间距0.75 m)和13 m高支撑架(加强层间距1.0 m),两者的竖向沉降位移与承载力性能基本接近。加载初期三者竖向刚度基本接近,随着荷载增加,有加强层支撑架竖向刚度明显大于无加强层支撑架,但三者达到极限承载力最终破环时竖向沉降位移基本接近。
支撑架加载的过程中,宏观表现为立杆位移增加,微观伴随着立杆应变增加,引入缺陷进行全过程分析时,荷载-应变关系曲线、位移-应变关系曲线也是分析过程中应该考虑的重要因素。荷载-应变关系曲线、位移-应变关系曲线如图6所示。扣件式钢管支撑架所用钢材为Q235,此钢材屈服强度标准值为235 N/mm,屈服时应变为0.001 14,从图6a中可以看出,在立杆应变达到屈服应变以前,无论有无加强层,荷载-应变关系呈现弹性特征,有加强层支撑架弹性阶段承载力略高于无加强层支撑架;在立杆屈服以后,支撑架随着荷载增加,应变快速增加。从图6b中可以看出,在立杆应变达到屈服应变以前,无论有无加强层,侧向位移-应变关系呈现弹性特征;立杆进入屈服以后,支撑架随着荷载增加,侧向位移-应变关系呈现明显非线性特征,表现出应变增加速度明显快于侧向位移增加速度,有加强层的12.5 m高支撑架(加强层间距0.75 m)和13 m高支撑架(加强层间距1.0 m),两者侧向位移-应变关系全过程基本一致。从图6c中可以看出,在立杆应变达到屈服应变以前,无论有无加强层,竖向位移-应变关系呈现弹性特征,立杆进入屈服以后,支撑架随着荷载增加,竖向位移-应变关系亦呈现明显非线性特征,应变增加速度明显快于竖向位移增加速度,有加强层的12.5 m高支撑架(加强层间距0.75 m)和13 m高支撑架(加强层间距1.0 m),两者竖向位移-应变关系全过程较为接近。

图4 3个模型支撑架失稳形态

图5 荷载-变形时间历程
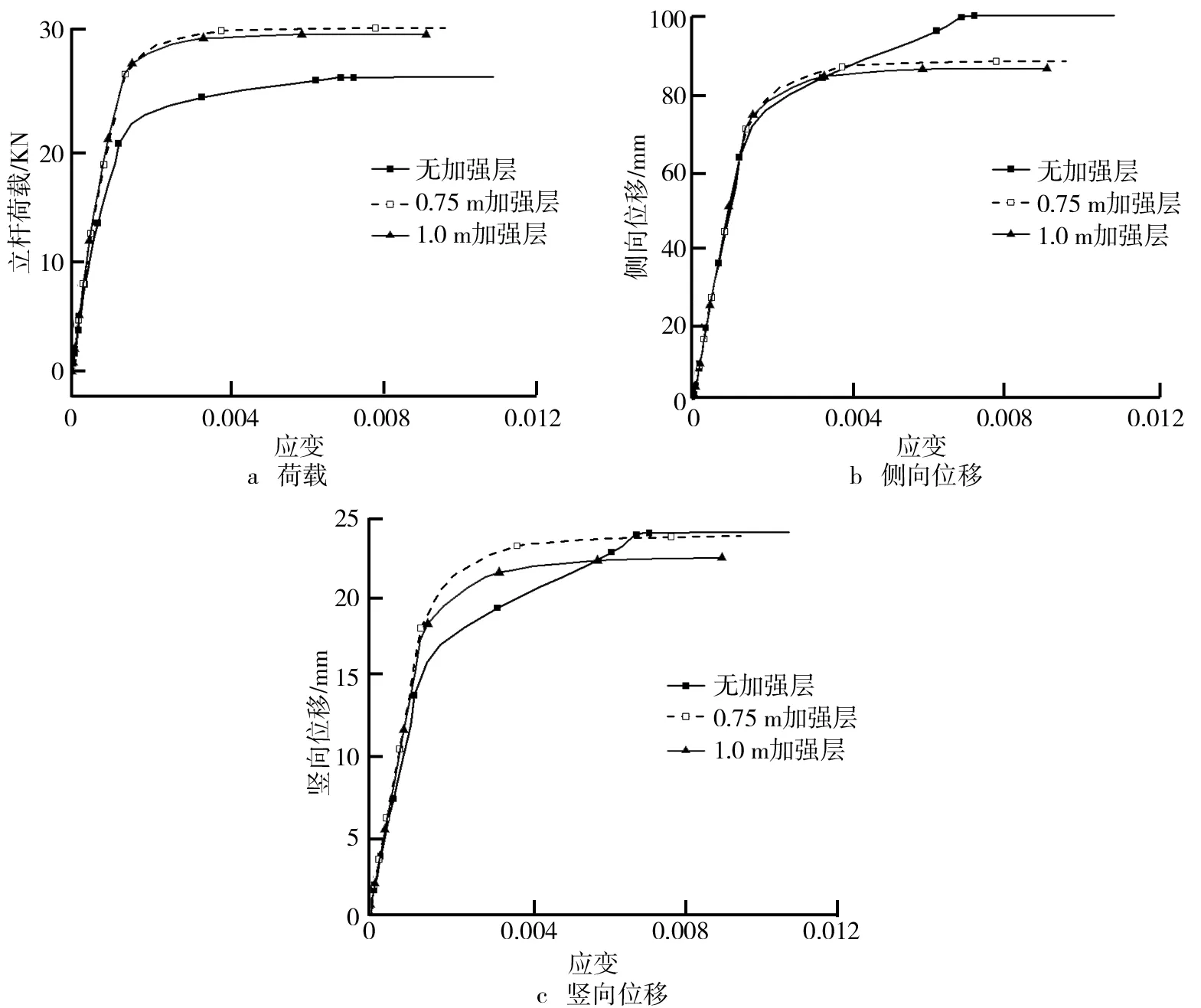
图6 荷载、位移-应变关系
结合上述分析,提取出支撑架刚进入屈服应变时对应的关键数据如表2所示。

表2 支撑架屈服时计算结果
将表1和表2中数据对比分析,进入屈服阶段和达到极限荷载破环阶段,承载力位移变化如表3所示。从表3中可以看出,屈服时对应承载力基本上是极限承载力的70%~75%,变化范围不大,加强层设置对其影响不明显;屈服时支撑架竖向位移基本上是达到极限承载力阶段竖向位移的50%~60%,变化范围亦基本稳定,加强层设置使支撑架屈服阶段竖向位移占极限承载力阶段竖向位移的比例提高;屈服时支撑架上部最大鼓曲位移基本上达到极限承载力阶段的55%~66%,变化范围亦基本稳定,加强层设置使支撑架屈服阶段上部最大鼓曲位移占极限承载力阶段比例提高。根据各阶段对比分析,工程监测应以立杆屈服以前作为控制荷载,通过观测顶部立杆沉降变形进行监测,对于高度在10 m以上支撑架,不论是否设置加强层,其立杆顶部竖向沉降变形控制值均为极限承载力阶段的50%~60%。为方便工程应用,对于10~15 m范围支撑架,建议可以偏安全地取立杆屈服时对应竖向沉降位移的70%进行监测控制。

表3 支撑架屈服阶段和极限阶段结果对比
3 小结
扣件式钢管支撑架加强层的设置对改变支撑架整体失稳形态影响不大,但对提高支撑架稳定承载力不容忽视,可以提高支撑架整体稳定承载力10%以上;扣件式钢管支撑架加强层的设置提高了支撑架屈服阶段,竖向沉降位移占支撑架整体极限承载力阶段竖向沉降位移的比例,对支撑架屈服阶段承载力占支撑架整体失稳极限承载力比例影响不明显;扣件式钢管支撑架加强层的设置与否,均建议工程监测应以支撑架立杆进入屈服时的支撑架顶部沉降位移的70%作为控制值。

