一种新的高精度全球对流层天顶延迟模型
黄良珂, 陈华, 刘立龙*, 姜卫平
1 桂林理工大学测绘地理信息学院, 桂林 541004 2 广西空间信息与测绘重点实验室, 桂林 541004 3 武汉大学卫星导航定位技术研究中心, 武汉 430079 4 武汉大学测绘学院, 武汉 430079
0 引言
对流层中蕴含着丰富的气体,当电磁波信号穿过对流层时,会使这些电磁波信号产生延迟,称为对流层延迟.对流层延迟是空间大地测量中最主要的误差源之一,其也是制约高精度全球导航卫星系统(GNSS)导航定位的重要因素.在GNSS精密数据处理中,常采用对流层延迟经验模型来估计出对流层天顶静力学延迟(ZHD)或ZTD作为初始值,如果模型计算的ZHD或ZTD初始值不精确,最终也会影响GNSS定位的精度.由此可见,高精度的对流层延迟经验模型显得尤为重要,尤其在全球坐标参考框架建立等GNSS 应用中.因此,建立实时高精度全球对流层延迟模型具有重要的现实意义.
对流层延迟改正模型主要可分为两大类,即需要实测气象参数的模型和实时对流层延迟模型(非气象参数模型).在依赖实测气象参数的对流层延迟模型中,国际上比较经典的有Hopfield(1971)、Saastamoinen(1972)和Black(1978)等对流层延迟模型.由于难以获取全球任意位置实时的实测气象参数,从而限制了需要实测气象参数的对流层延迟模型在GNSS导航和实时定位中的应用.为了满足对流层延迟应用需求的实时性,利用大气再分析资料构建区域或者全球的实时对流层延迟模型获得广泛关注,如UNB系列模型(Leandro et al.,2006,2008)和EGNOS模型(Penna et al.,2001)等.近年来,随着GPS/GNSS导航定位技术的发展,诸多学者对实时对流层延迟改正模型的构建给予了极大的关注.如国外学者构建的TropGrid系列模型(Schüler,2014)和 GPT系列模型(Böhm et al.,2007,2015; Lagler et al.,2013).与此同时,中国学者在这方面也取得了丰硕的成果,Song等(2011)利用多年欧洲中尺度天气预报中心(ECMWF)大气再分析资料,构建了适用于中国区域的对流层天顶延迟模型(简称SHAO模型),其在中国地区的改正精度相对于EGNOS模型提升显著.黄良珂等(2014)使用数年IGS站的高精度ZTD数据对EGNOS模型在亚洲地区进行了单站精化,构建了亚洲地区的精化模型(SSIEGNOS模型),SSIEGNOS模型能取得较好的单站ZTD改正效果,且在长期的ZTD预报中能保持稳定的性能.李薇等(2012)在分析ZTD时空特性基础上,利用多年的美国环境预报中心(NCEP)再分析资料建立了一种全球格网ZTD新模型——IGGtrop模型,该模型在全球范围内获得了较好的精度.Li等(2015)对IGGtrop模型进行改进,发展了IGGtrop_ri(i=1,2,3)模型,新模型对赤道区域进行了简化,并极大地减少了模型参数,使新模型更好地应用于北斗/GNSS的对流层延迟改正.姚宜斌等(2013)利用GGOS大气中心提供的2°×2.5°(纬度×经度)分辨率ZTD格网数据,结合球谐函数构建了全球非气象参数GZTD模型, GZTD模型表现出了良好的对流层修正效果.此外,姚宜斌等(姚宜斌等,2015; Yao et al.,2015)先后构建了高时间分辨率的GZTD-6h模型和ITG格网模型,新模型相比于GZTD模型其精度有一定的改善,并提高了时间分辨率.赵静旸等(2014)利用ECMWF中心提供的ERA-Interim资料,构建了顾及垂直剖面函数的全球非气象参数对流层延迟模型(SHAO-H模型),该模型具有精度稳定、可适用于任意高度对流层延迟修正等优点.姚宜斌等(2016)联合GGOS大气格网ZTD和IGS中心提供的精密ZTD产品,以Delaunay三角网的形式存储模型参数,进而构建了多源数据联合的全球ZTD模型,新模型表现出全球适用和区域增强的优点.Sun等(2017)基于非线性假设,利用GGOS大气ZTD格网产品构建了顾及ZTD年周期、半年周期、4个月变化和季度变化的全球ZTD格网模型(GZTDS模型),并结合GZTDS和VMF1模型建立了GSTDS模型,结果表明GZTDS模型计算ZTD的性能与GPT2w模型相当.Li等(2018)分别采用指数函数和多项式函数去表征ZTD垂直剖面函数的平均值和振幅,最终构建了两个非气象参数的全球ZTD模型,即IGGtrop_SH和IGGtrop_rH模型,这两个新模型均表现出良好的ZTD改正性能,IGGtrop_SH模型的性能略优于IGGtrop_rH模型.Sun等(2019)利用长期的ERA-Interim数据分析了对流层垂直递减率的精细季节变化,在此基础上构建了高水平分辨率的全球格网对流层模型(GTrop模型),结果表明该模型较好地改善了在高海拔地区的ZHD估计精度.
尽管上述区域或全球对流层延迟模型均表现出各自的优越性,但仍存在模型方程未同时顾及高程和纬度因子的影响,且模型构建仅使用单一格网点数据等不足.相关研究表明ZTD与高程和纬度均存在显著的相关性,为此,本文提出引入滑动窗口算法将全球剖分为大小一致的规则窗口,使用多年的全球GGOS大气格网ZTD产品及对应的椭球高数据,构建全球每个窗口同时顾及高程、纬度和季节变化的ZTD模型,最终建立一种新的高精度全球ZTD格网模型(简称GGZTD模型),并以未参与建模的全球GGOS大气格网ZTD数据及全球IGS站精密ZTD产品为参考值,验证GGZTD模型在全球的适用性.
1 ZTD时空特性分析与GGZTD模型构建
1.1 ZTD时空特性分析
相关文献研究表明ZTD时间序列主要表现为年周期和半年周期变化,同时在部分地区也表现出一定的日周期变化(姚宜斌等,2013),为了进一步验证ZTD值的年周期、半年周期和日周期振幅在全球的分布,利用2010—2015年水平分辨率为2°×2.5°、时间分辨率为6 h的全球GGOS大气格网ZTD数据,采用式(1)来计算出全球各格网点ZTD值不同周期的振幅值,结果如图1所示.
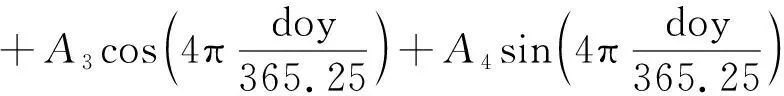
(1)
式中,A0表示ZTD年均值,(A1,A2)、(A3,A4)和(A5,A6)分别表示ZTD的年周期、半年周期和日周期的系数,doy表示年积日,hod表示UTC时间.
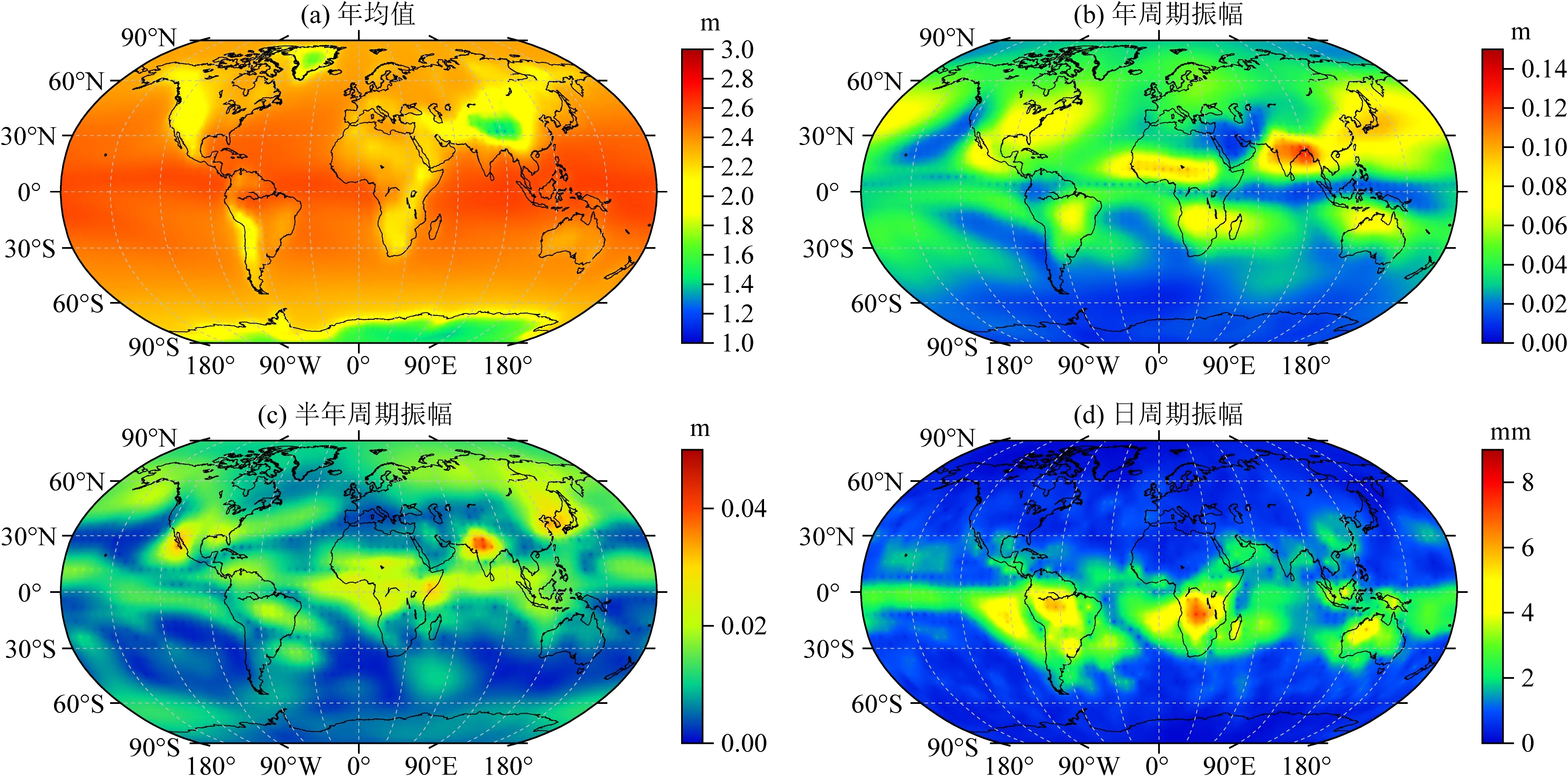
图1 GGOS格网ZTD数据计算全球ZTD平均值、年周期、半年周期和日周期分布Fig.1 Distributions of the mean value, annual, semi-annual and diurnal amplitudes of ZTD derived from GGOS Atmosphere gridded ZTD products over globe
由图1可知,ZTD平均值的分布与高程和纬度存在较大关系,其在青藏高原、南极和格陵兰等高海拔地区的值较小,在海洋地区其平均值较大;对于ZTD年周期振幅,其在北半球的年周期振幅值高于其在南半球的值,在太平洋西部、亚洲东部和南部、北美洲东南部、非洲、澳大利亚北部等地区表现出显著的年周期振幅值,在南半球的中高纬度地区其值相对较小;对于ZTD的半年周期振幅,其在北半球的值仍然大于南半球,在中国东北部、亚洲东南部和低纬度的部分地区存在显著的半年周期振幅值,在南半球的中高纬度地区仍表现出相对较小的值;对于ZTD的日周期振幅,其在低纬度的部分地区表现出相对较大的日周期振幅值,尤其在南美洲中部和非洲南部地区存在4~8 mm的日周期振幅值,但是在全球大部分地区ZTD的日周期变化较小,其值低于2 mm.由于在低纬度地区,ZTD的年周期和半年周期相对较为显著,此外,该地区的气候较为复杂,其引起的ZTD的变化也较为剧烈,尽管在该地区的部分区域存在4~8 mm的日周期变化,那么在ZTD建模时,这些相对较小的ZTD日周期变化容易被ZTD年周期和半年周期的模型化残差及其他非季节性信号淹没.因此,为了优化ZTD建模的模型参数,提高模型的计算效率,本文模型构建时对ZTD的季节变化只考虑其年周期和半年周期.
对于ZTD在高程上的变化关系方面,常用的ZTD垂直剖面函数主要有二次多项式和负指数函数.Song等(2011)指出在10 km以下用二次多项式来表达ZTD的垂直剖面可获得较好的ZTD高程改正效果.赵静旸等(2014)提出了ZTD的分段垂直剖面函数,在17 km以下的大气层范围内利用多项式来表达ZTD的垂直剖面,17 km以上采用负指数函数来进行表达,该分段ZTD垂直剖面模型获得了良好的ZTD高程改正效果.由于本文构建全球ZTD模型时采用的是全球GGOS大气格网ZTD产品及对应的地表椭球高数据,为了进一步探究地表至17 km高度范围内ZTD在高程上的变化,本文选取了全球具有代表性的MERRA-2分层大气资料的4个格网点数据,利用积分法计算出4个格网点(地表至17 km高度范围内)2015年1月1日0时刻的ZTD分层剖面信息,并采用二次多项式对其进行拟合,结果如图2所示.图2表明在地表至17 km高度范围内,利用二次多项式可较好地反映ZTD值在高程上的变化.同时,为了进一步分析ZTD在纬度上的变化,选取经度为170°W和170°E的所有格网点数据,针对每个格网点均从500 m开始积分到MERRA-2再分析资料最顶层,进而分析ZTD随纬度的变化关系,结果如图3所示.由图3可知,在一定纬度范围内ZTD在纬度上的变化可表示为近似线性关系.因此,在本文ZTD建模中将采用二次多项式来描述ZTD的垂直剖面改正,ZTD在纬度上变化采用线性函数.

图2 ZTD在高程上变化关系Fig.2 ZTD changes with altitude
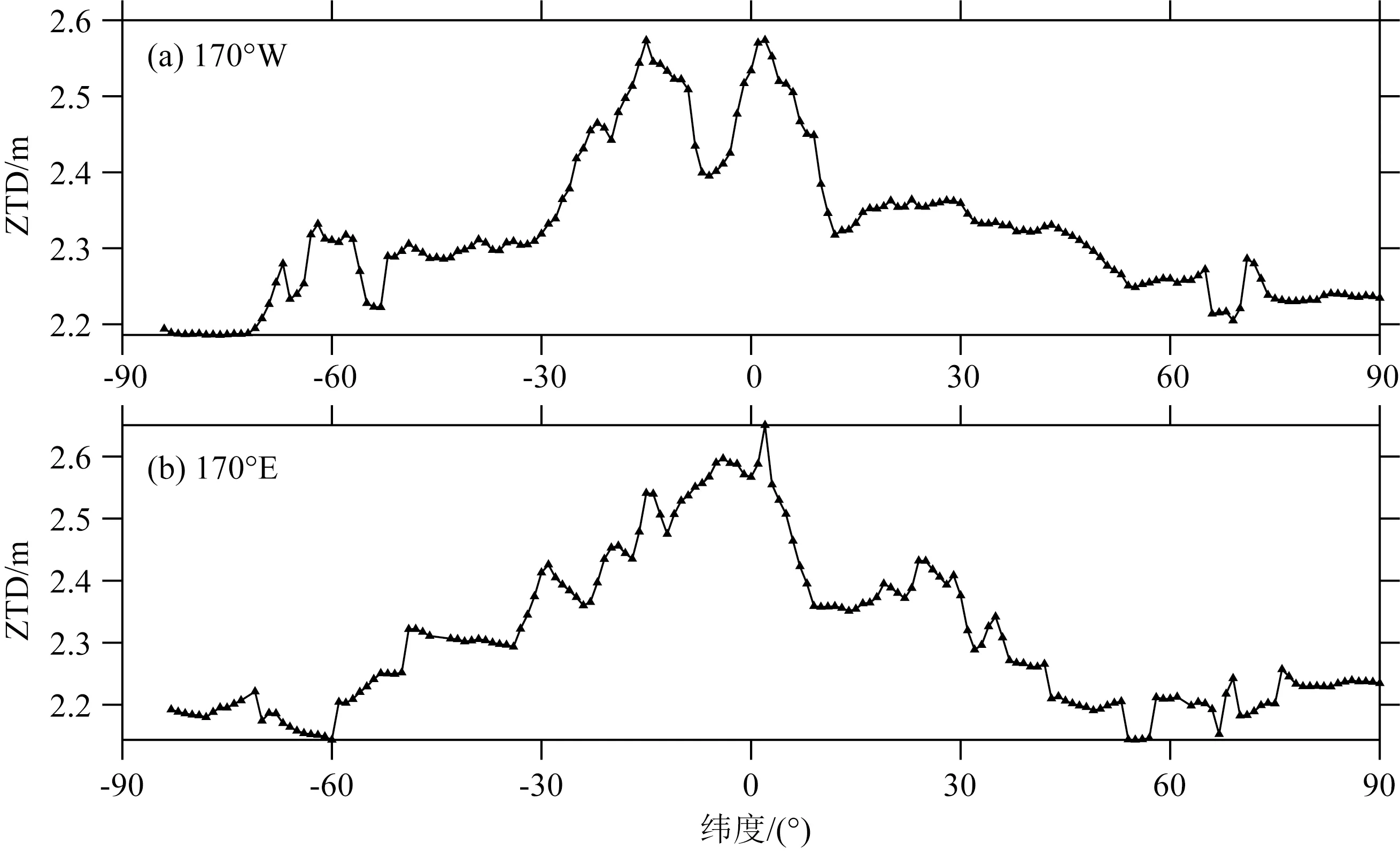
图3 ZTD在纬度上变化关系Fig.3 ZTD changes with latitude
1.2 GGZTD模型建立
针对当前全球对流层经验模型的模型方程未同时顾及高程和纬度的变化及模型构建仅使用单一格网点数据等问题,结合上述对ZTD的时空特性分析,引入滑动窗口算法来解决以上问题.在此,先对滑动窗口的算法做如下简述.
首先以平面分辨率为2°×2.5°(纬度×经度)进行全球格网剖分,得到与GGOS大气格网产品相同大小水平分辨率的格网.滑动窗口算法的关键需要确定其窗口的大小及其滑动步长,滑动窗口大小的确定需顾及全球窗口剖分个数的整数性、窗口的连续性及窗口内模型参数的可求解性等原则.根据以上原则,本文以3行3列(4°×5°的区域范围)为一个滑动窗口大小来举例说明滑动窗口算法,其流程如图4所示.具体过程为:首先利用格网左上角第一个窗口N1内(每个框表示一个滑动窗口大小)的数据求出其窗口内的相关模型参数,并将其作为窗口N1中心格网点(框内黑点)的结果;然后将窗口向纬度东向移动2个格网点,求解新窗口N2内的相关模型参数,将其作为窗口N2中心格网点的结果,依次类推求出这一纬度上所有窗口内的相关模型参数;然后窗口移动到下一纬度(向下移动两个格网点),以同样的方法求出该纬度所有窗口内的相关模型参数,以此类推直到求出全球所有窗口内的相关模型参数.最终获得全球所有窗口内的相关模型参数,并将其作为各自窗口中心格网点的结果,最后将全球所有窗口中心格网点组建新的全球格网,如图4中的黑点和虚线所示.
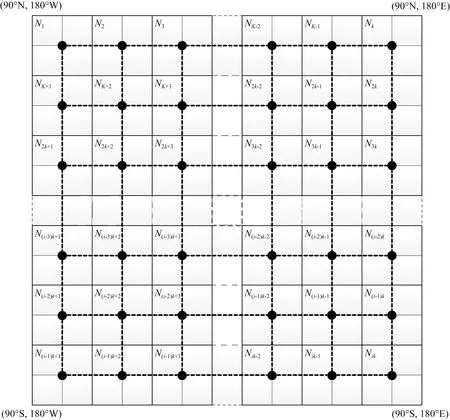
图4 滑动窗口算法示意图Fig.4 The schematic of sliding window algorithm
本文仅探索使用固定的窗口大小(4°×5°)和滑动步长来构建全球ZTD模型,即每个窗口包含了9个格网点,针对每一个窗口,GGZTD模型在时间尺度上主要考虑ZTD的年周期和半年周期特性,在空间尺度上同时顾及ZTD在纬度和高程上的变化,由此可确定全球每个窗口内的ZTD模型方程如下:
ZTD(φ,h,doy)=f1(φ,h)+f2(doy),
(2)
其中φ,h分别表示纬度和高程,doy表示年积日,f1(φ,h)表示纬度和高程对ZTD的共同影响,f2(doy)表示ZTD的季节变化,其分别可表示为
f1(φ,h)=a0+a1φ+a2h+a3h2,
(3)
(4)
最终可将式(2)改写为
ZTD(φT,λT,h,doy)=C0(φi,λi)+C1(φi,λi)·φT+C2(φi,λi)·h+C3(φi,λi)·h2
(5)
式中,(φi,λi)表示第i个窗口的几何中心的纬度和经度,单位均为度;φT,λT和h分别表示目标点的纬度(单位是°)、经度(单位是°)和高程(单位是m).C0表示ZTD的年均值,C1表示纬度改正系数,C2和C3表示高程改正系数,(C4,C5)和(C6,C7)分别表示ZTD的年周期和半年周期系数.利用2008—2015年水平分辨率为2°×2.5°的全球GGOS大气格网ZTD地表数据和对应的全球椭球高数据,根据式(5)采用最小二乘算法即可求解出全球每个窗口的模型系数,最终GGZTD模型的模型系数以4°×5°的格网形式存储.GGZTD模型在全球包含了3240个格网点.
GGZTD模型的使用非常简便,其使用过程如下:(1)用户提供doy和目标点位置信息,根据目标点位置信息查找与目标点最近的模型参数格网点;(2)根据获得的最近的模型参数格网点的模型参数,并利用式(5)即可计算出目标点的ZTD信息.
2 GGZTD 模型精度验证
为了验证 GGZTD 模型在全球的精度和适用性,选取未参与建模的全GGOS 大气格网 ZTD 产品和全球 IGS 中心提供的 GNSS ZTD 产品为参考值来验证 GGZTD 模型的精度,并与目前精度标称最优的 GPT2w 模型(Böhm et al., 2015)和全球广泛使用的 UNB3m 模型(Leandro et al., 2008)进行精度对比,由于GPT2w模型可提供水平分辨率分别为1°×1°和5°×5°的格网参数,便于后续描述,分别将其简写为GPT2w-1和GPT2w-5.同时,以 bias(偏差)和 RMS 误差作为精度指标来评判模型的精度.
2.1 与全球 GGOS 大气格网 ZTD 产品比较
以GGOS中心提供的未参与建模的2016年时间分辨率为6 h(UTC 00∶00,06∶00,12∶00和18∶00)的全球GGOS大气格网ZTD地表产品为参考值,同时计算出GGZTD、GPT2w-1、GPT2w-5和UNB3m模型在这些格网点处对应时间的ZTD值,由此可获得这些模型计算ZTD的bias和RMS值,结果如表1、图5和图6所示.
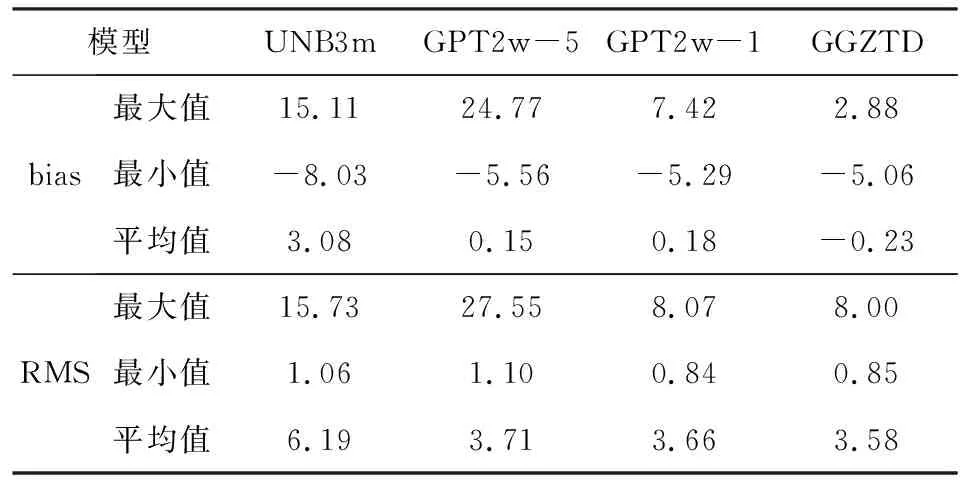
表1 2016 年全球 GGOS 大气格网 ZTD 产品验证 GGZTD、GPT2w-5、GPT2w-1和UNB3m模型的精度统计(单位:cm)Table 1 Error statistics of GGZTD、GPT2w-5、GPT2w-1 and UNB3m models tested using GGOS Atmosphere gridded ZTD data in 2016 (Unit: cm)
由表1可知,GGZTD模型表现出较小的bias值和最小的RMS,平均bias值和RMS分别为-0.23 cm和3.58 cm,其bias值和RMS变化范围分别为-5.06 cm到2.88 cm和0.85 cm到8.00 cm;GPT2w-5表现出了最大的bias和RMS值,分别为24.77 cm和27.55 cm,GPT2w-1的性能相对较为稳定且精度优于GPT2w-5,由此表明GPT2w模型通过提高其模型参数的空间分辨率对其精度具有一定的改善;而UNB3m模型表现出最大的平均bias和RMS值分别为3.08 cm和6.19 cm,说明UNB3m模型在全球存在显著的系统偏差,主要原因是UNB3m模型提供的模型参数的空间分辨率较低.在RMS方面,相对于GPT2w-1、GPT2w-5和UNB3m模型,GGZTD模型在全球计算ZTD的精度分别提升了0.8 mm、1.3 mm和26.1 mm(42%).由此可见,GGZTD模型的精度相对于UNB3m模型具有显著的提高,同时相对于目前性能优异的GPT2w模型也具有一定的改善.
图5表明UNB3m模型在南半球高纬度地区(纬度大于60°)、印度洋、太平洋及亚洲西南部和非洲南部的部分地区出现较大的正bias值,在低纬度(30°S—30°N)的部分地区存在显著的负bias值,其在北半球的bias值明显小于南半球.相对于UNB3m模型,GPT2w-5和GPT2w-1均表现出相对较小的bias值,但是在太平洋东部和南半球高纬度的部分地区仍然存在相对较大的正bias值,尤其是GPT2w-5在北美洲南部和印度洋东部的部分地区存在较大的正bias值且在该地区出现最大的bias值,而在低纬度地区的大西洋、南美洲北部和非洲中部及太平洋南部的部分地区存在相对较大的负bias值,而GGZTD在全球范围内均表现相对较小的bias值,其仅在低纬度的小部分区域存在相对较大的负bias值.

图5 2016 年全球 GGOS 大气格网 ZTD 产品验证不同模型的bias值全球分布Fig.5 Distributions of the bias validated using GGOS Atmosphere gridded ZTD data for all models in 2016 over globe
由图6可知,UNB3m模型在整个南半球区域及北半球低纬度地区存在较大的RMS,尤其在南半球高纬度地区、印度洋东部和太平洋部分地区,其在南半球的精度也明显低于北半球,主要原因是受UNB3m模型的南北半球对称假设的影响(Leandro et al., 2008),此外,UNB3m模型在低纬度地区未考虑模型参数的年际变化;相对于UNB3m模型,GPT2w-5、GPT2w-1和GGZTD模型在全球范围内表现出较小的RMS,但是在低纬度的部分地区(如大西洋、非洲、太平洋东部地区、中国东南部和澳大利亚)表现出相对较大的RMS,尤其是GPT2w-5在北美洲南部的部分地区,由于在这些地区受深对流、热带海洋气候和热带雨林气候等复杂气候系统的综合影响,进而引起ZTD的剧烈变化,因此难以对ZTD进行精确模型化;此外,相对于其他地区,低纬度地区的ZTD具有较为显著的日周期变化(姚宜斌等, 2016),而这三种模型均未顾及ZTD的日周期变化,从而导致所有模型在该地区均存在较大的误差.尽管如此,相对于GPT2w模型计算的ZTD信息,GGZTD模型在太平洋东部、大西洋、北美洲南部和南极的部分地区仍具有一定的精度提升.因此,相对于UNB3m模型,GGZTD模型在全球估计ZTD的精度具有显著的提高;而相对于目前性能优异的GPT2w模型,GGZTD模型在部分地区仍具有一定的精度改善.总之,相对于其他两种模型,GGZTD模型在全球估计ZTD表现出稳定和优异的性能.
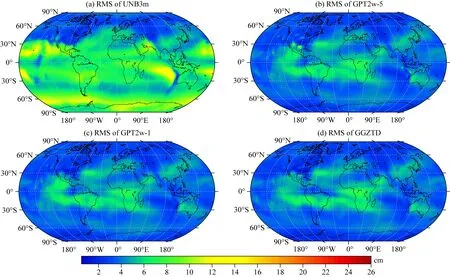
图6 2016年全球GGOS大气格网ZTD产品验证不同模型的RMS全球分布Fig.6 Distributions of the RMS error validated using GGOS Atmosphere gridded ZTD data for all models in 2016 over globe
2.2 与全球IGS站ZTD产品比较
IGS中心能提供全球IGS站的精密ZTD产品,其时间分辨率为5 min,精度优于5 mm(Byun and Bar-Sever, 2009),为了进一步验证GGZTD模型在全球的精度,利用2016年全球IGS站精密ZTD产品作为参考值对其进行精度检验.由于部分IGS站的数据缺失较为严重,为了保证验证的可靠性,选取了数据量至少含有120天的IGS站参与模型检验,最终在全球选取了2016年的316个IGS站,其点位分布如图7所示.以2016年全球316个IGS站精密ZTD产品为参考值,同时计算出GGZTD模型、UNB3m模型和GPT2w模型在这些IGS站的ZTD值,最终获得这些模型的bias和RMS值的统计结果,如表2、图8和图9所示.
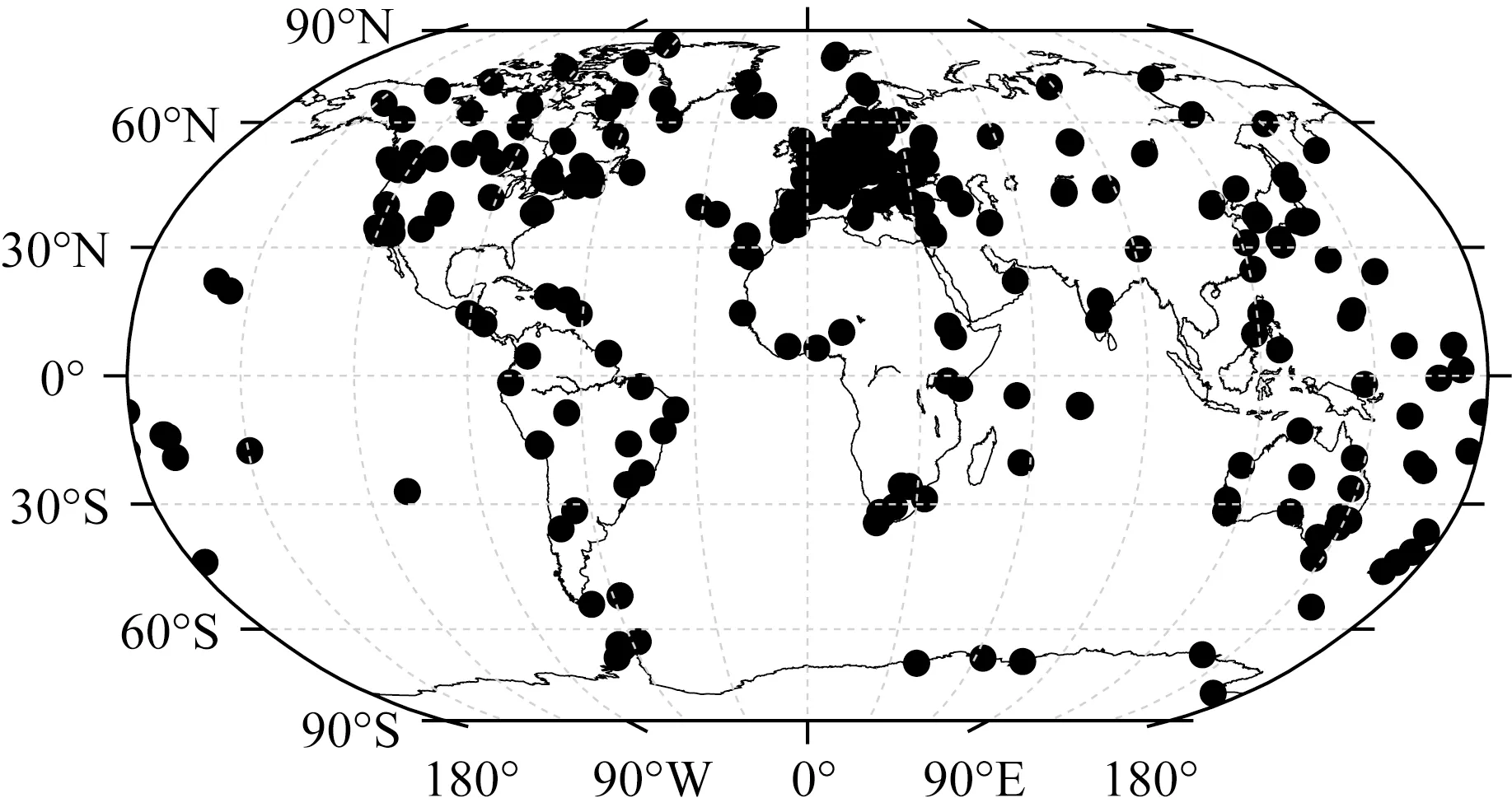
图7 全球316个IGS站的点位分布Fig.7 The distribution of 316 IGS stations over globe
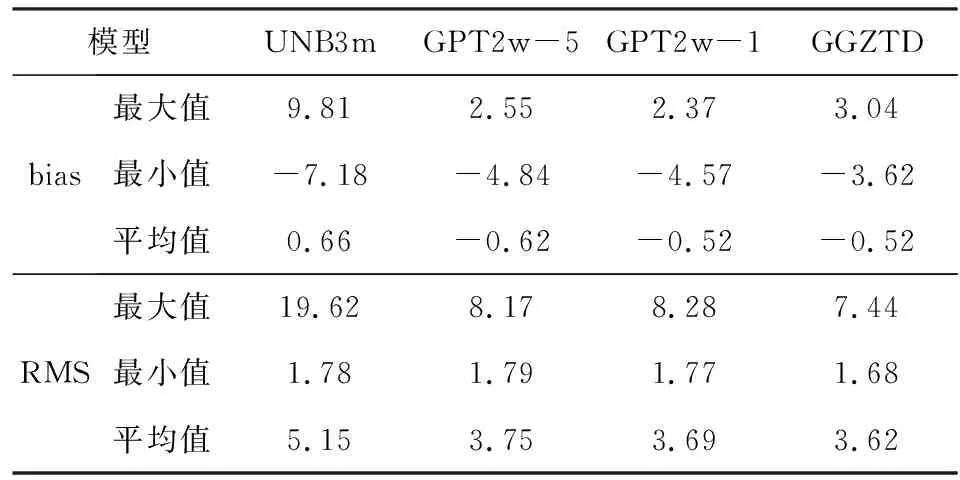
表2 2016年全球316个IGS站ZTD产品验证GGZTD、GPT2w-5、GPT2w-1和UNB3m模型的精度统计(单位:cm)Table 2 Error statistics of GGZTD、GPT2w-5、GPT2w-1 and UNB3m models tested using 316 IGS ZTD data in 2016 over globe (Unit: cm)

图8 2016年全球IGS站ZTD产品验证不同模型的bias值全球分布Fig.8 The distributions of the bias validated using IGS ZTD data in 2016 over globe
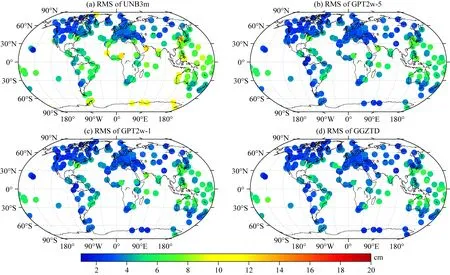
图9 2016年全球IGS站ZTD产品验证不同模型的RMS全球分布Fig.9 The distributions of the RMS error validated using IGS ZTD data in 2016 over globe
由表2可知,UNB3m模型表现出最大的平均bias和RMS值,其分别为0.66 cm和5.15 cm,与GGOS大气ZTD格网产品验证结果一致.GPT2w-5、 GPT2w-1和GGZTD模型均表现出负bias值,说明这些模型估计值偏小;相对于UNB3m模型,GPT2w-5和GPT2w-1表现出相对较小的平均RMS值分别为3.75 cm和3.69 cm,GPT2w-1相对于GPT2w-5其精度提升了0.6 mm,进一步说明GPT2w模型通过改善模型参数的空间分辨率能在一定程度上提高其ZTD估计的精度.而GGZTD模型在所有模型中表现出最优的性能,其RMS变化范围为1.68~7.44 cm,平均值为 3.62 cm,相对于UNB3m模型、GPT2w-5和GPT2w-1,其在全球估计ZTD的精度分别提升了15.3 mm(30%)、1.3 mm和0.7 mm.进一步表明GGZTD模型在全球范围内的精度相对于UNB3m模型具有显著的提升,相对于性能优异的GPT2w模型仍具有一定的改善.
由图8可以看出,UNB3m模型在南半球中高纬度地区、澳大利亚、非洲北部、北美洲东部和西南部地区存在显著的正bias值,在低纬度、亚洲和欧洲的部分地区存在显著的负bias值,在南半球的bias值要高于北半球.相对于UNB3m模型,GPT2w-5和GPT2w-1在全球范围内表现出相对较小的bias值,只有在临近赤道的PNGM站出现了较大的负bias值,可能受赤道附近复杂的气候影响.而GGZTD在全球范围内均表现出稳定和相对较小的bias值,且在南北半球的bias值分布较为均匀.图9表明,在RMS方面,UNB3m模型在南半球和低纬度地区仍表现出较大的RMS值,尤其在南极地区,且在南半球的RMS值明显大于北半球,这与GGOS大气格网ZTD产品验证结果一致,进一步说明UNB3m模型的南北半球假设不合理、模型参数空间分辨率偏低和低纬度地区未顾及年际参数变化.相对于UNB3m模型,GPT2w模型和GGZTD模型在全球均展现出相对较小且稳定的RMS,但是其在低纬度地区的太平洋和印度洋的GNSS测站中存在相对较大的RMS,由于在这些地区受热带海洋气候和热带雨林气候等复杂气候系统的综合影响,从而在ZTD信息中引入了非季节性变化信号,导致了ZTD的异常扰动,因此难以对ZTD进行精确模型化.此外,相对于中高纬度地区,低纬度地区ZTD也存在较为显著的日周期变化,然而GPT2w模型和GGZTD模型未顾及日周期变化,从而在模型中引入了未模型化的误差.尽管如此,相对于GPT2w模型,GGZTD模型在非洲东部、中国东部、欧洲和南极地区的部分GNSS测站中仍表现出相对优越的性能.
此外,为了进一步分析这些模型的精度分布情况,对其bias和RMS结果进行了精度统计,结果如图10和图11所示.图10表明,从误差分布直方图可看出UNB3m模型具有较小的平均正bias值,但是仍然表现出较大数量的正负bias值的个数,其较大正bias值的个数大于较大负bias值的个数,说明UNB3m模型在全球大部分区域估计的ZTD值大于IGS-ZTD值.GPT2w-5、GPT2w-1和GGZTD模型均表现出较小的平均负bias值,相对于GPT2w-5和GPT2w-1,GGZTD模型的bias值分布更为集中,而GPT2w-5相对于GPT2w-1的bias分布则较为分散,由此说明GGZTD模型比GPT2w模型和UNB3m模型更具稳定性.由图11可知,对于UNB3m模型,其RMS在3~4 cm的范围占据了最大的比例为34%,而小于3 cm的比例仅为10%,大于6 cm的比例高达31%.相对于UNB3m模型,GPT2w-5和GPT2w-1的RMS分布具有明显的改善,GPT2w-5的RMS在低于3 cm的比例中占据了29%(GPT2w-1为32%),而大于6 cm的RMS比例低至6%(GPT2w-1为5%),其在低于4 cm的比例分别为68%和71%.在所有模型中,GGZTD模型在小于3 cm和小于4 cm的RMS分布中均占据了最大比例,其比例分别高达为35%和73%,此外,其在大于6 cm的RMS比例中具有最小值,低至4%.在低于3 cm的RMS比例中,相对于UNB3m模型、GPT2w-5和GPT2w-1,GGZTD模型分别提高了25%、6%和3%,在低于4 cm的RMS比例中,其分别提高了29%、5%和2%.由此进一步表明相对于UNB3m模型和GPT2w模型,GGZTD模型在全球范围内具有稳定的ZTD估计性能及最优的精度.
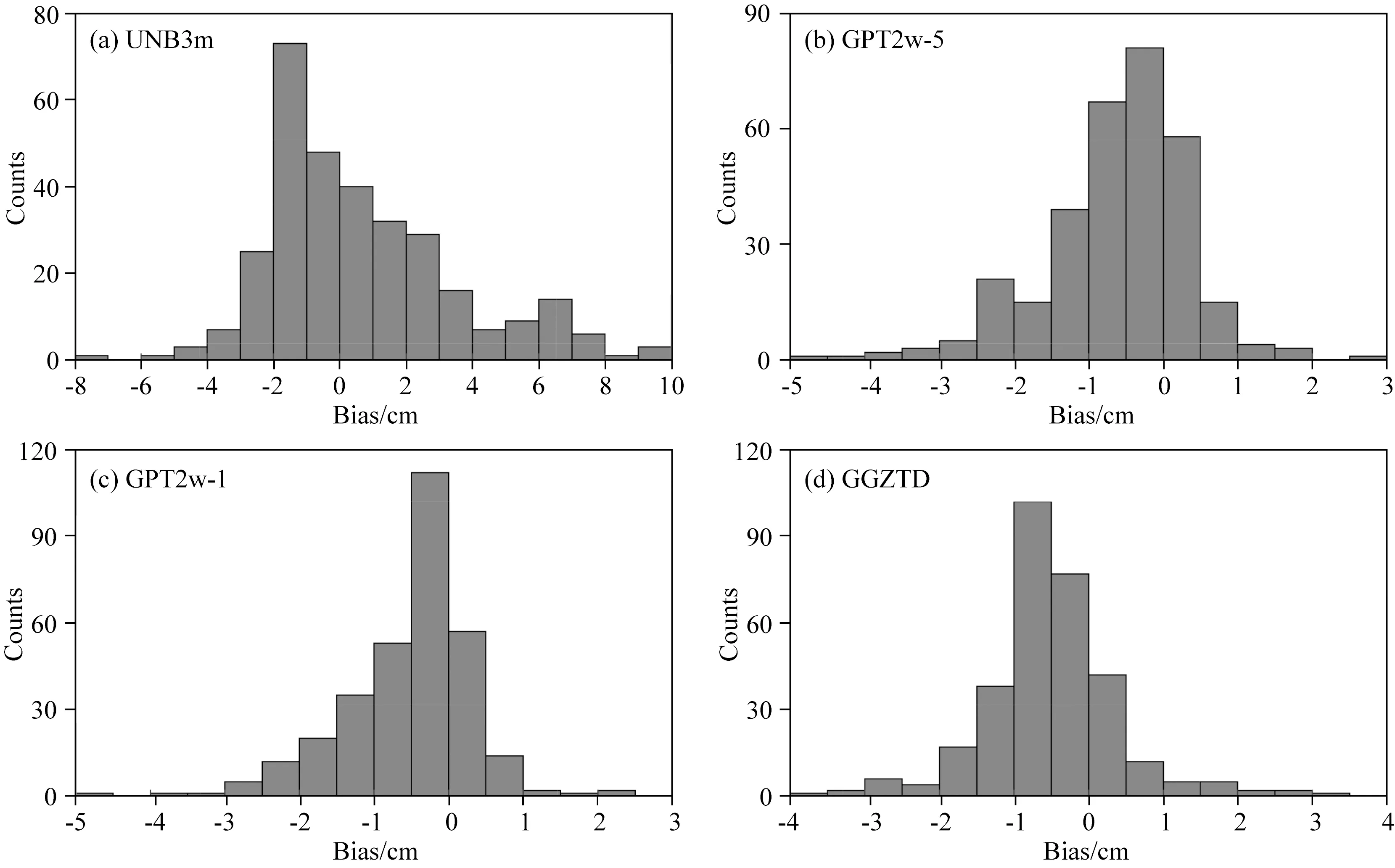
图10 2016年全球IGS站ZTD产品验证不同模型的bias值直方分布图Fig.10 Histogram of bias for different models tested with IGS ZTD data in 2016 over globe
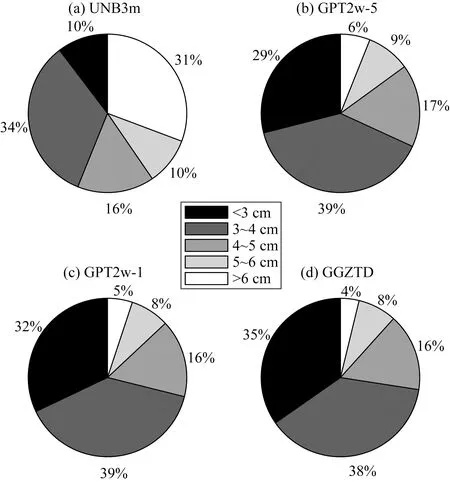
图11 2016年全球IGS站ZTD产品验证不同模型的RMS比例分布Fig.11 Proportional distribution of RMS values for different models tested with IGS ZTD data in 2016 over globe
为了分析GGZTD模型、GPT2w模型和UNB3m模型的季节变化性能,在全球南北半球的高、中和低纬度地区分别挑选了数据较为齐全的6个具有代表性的IGS站,即KELY站、BJFS站、BJCO站、PNGM站、DUND站和SYOG站,用于参与模型的季节变化性能分析,图12给出了所有模型估计的对应测站的ZTD日均bias时序图.

图12 不同模型估计的2016年ZTD值在6个IGS站的bias时间序列(括号内表示每个测站的纬度、经度和高程)Fig.12 Time series of ZTD bias for different models compared to the IGS data in 2016(the brackets indicate the latitude, longitude and altitude of each station)
由图12可知,位于北半球高纬度地区的KELY站,所有模型在春季表现为显著的负bias值,在其他季节的变化不明显;对于北半球中纬度地区的BJFS站,所有模型在夏季均表现出较大的bias值(以负bias值为主),说明北半球的夏季水汽变化较为剧烈,导致所有模型的ZTD估计值低于其实测值,在其他季节里UNB3m模型存在显著的正bias值,而GGZTD模型和GPT2w模型的变化不明显,且在春季和冬季表现出较小的bias值;对于低纬度地区的BJCO站和PNGM站,UNB3m模型在全年均表现为显著的负bias值,除了在BJCO站的冬季表现为显著的正bias值外.对于南半球中纬度地区的DUND站,所有模型在春季和冬季均表现出较大的bias值,尤其是UNB3m模型,在夏季和秋季则表现为相对平稳的bias值,可能是受南半球中纬度地区冬季和春季的水汽变化剧烈的影响;对于南半球高纬度地区的SYOG站,UNB3m模型在全年均表现出较大的正bias值,尤其在春季和冬季,GPT2w-5在春季和夏季表现出相对明显的正bias值,而GGZTD模型和GPT2w-1在全年均体现出相对较为稳定的bias值,相对于GPT2w-1, GGZTD模型在秋季表现出更为稳定和较小的bias值.由此表明,UNB3m模型在全球范围内估计ZTD的bias值存在明显季节变化,进一步说明UNB3m模型的模型参数空间分辨率低下以及南北半球对称的假设不合理,导致了UNB3m模型在南半球使用存在较大的偏差,尤其在南半球低纬度地区,而GGZTD模型和GPT2w模型估计ZTD的bias值存在相对较小的季节变化,相对于GPT2w模型,GGZTD模型在低纬度地区估计ZTD值具有显著的精度改善,其能更好地捕捉ZTD的季节变化.
为了进一步分析所有模型估计ZTD的bias值和RMS在高程上的变化关系,对全球316个IGS站按照500 m高程间隔进行分类,最终可分为低于500 m,500~1000 m,1000~1500 m、1500~2000 m和大于2500 m等5个高程范围,统计不同模型在每个高程范围内的bias值和RMS,结果如图13所示.
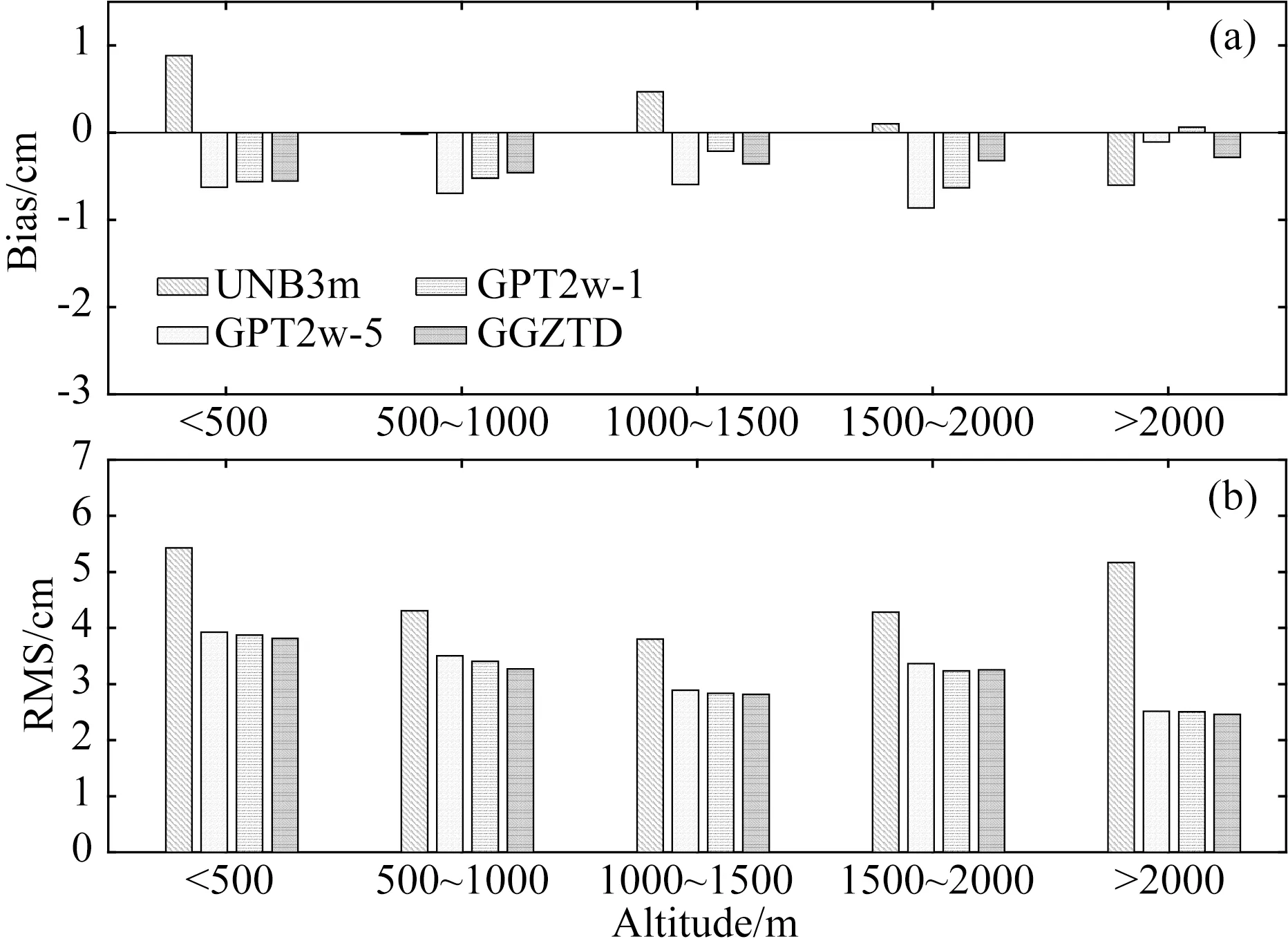
图13 2016年全球IGS站ZTD产品验证各模型的bias和RMS在不同高程范围内的变化Fig.13 Bias and RMS error statistics for different models tested with ZTD from IGS products in different altitude range in 2016
图13表明,UNB3m模型在海拔大于2000 m时存在较大的负bias值,GPT2w-5、GPT2w-1和GGZTD模型在低于2000 m的高程范围内均体现出相对明显的负bias值,所有模型的bias值在高程上无明显的变化关系,相对于GPT2w模型,GGZTD模型在1500~2000 m高程范围内具有较小的绝对bias值.UNB3m模型的RMS在高程上未发现明显的变化关系,尽管如此,其在低于500 m和大于2000 m的高程范围内存在较大的RMS,但是总体上,GPT2w-5、GPT2w-1和GGZTD模型的RMS在高程上均存在随着高程的增大而减小.此外,位于低纬度地区的IGS站其高程大部分低于500 m,导致低于500 m高程范围的RMS较大,且随着高程的增加水汽的含量及其变化也相应递减,从而更易于对ZTD模型化.
如前所述,纬度也是影响ZTD的主要变化因子.为了进一步分析不同模型估计ZTD的bias值和RMS在纬度上的变化关系,对全球316个IGS站按照15°的纬度间隔进行分类,统计不同模型在每个纬度范围内的bias值和RMS,结果如图14所示.
由图14可知,UNB3m模型在南半球15°以上范围存在较大的正bias值,尤其在南半球高纬度地区,而GPT2w-5、GPT2w-1和GGZTD模型在全球各纬度范围内均体现出相对较小的负bias值,相对于GPT2w模型,GGZTD模型在15°S—15°N纬度范围内表现出相对较小的绝对bias值.在RMS方面,UNB3m模型在南半球的纬度范围内的值明显大于北半球,尤其在南半球的高纬度地区,此外,在低纬度地区也存在相对较大的RMS.对于GPT2w-5、GPT2w-1和GGZTD模型,总体上其RMS均存在以赤道向两极减小的趋势.相对于UNB3m模型,GGZTD模型在整个南半球和北半球的低纬度地区具有显著的精度改善,尤其在南半球;相对于GPT2w模型,GGZTD模型在南半球纬度大于75°区域和北半球低纬度地区仍具有一定的精度提升,尤其在南半球纬度大于75°区域.由此表明GGZTD模型在所有对比的模型中具有稳定和优越的性能,尤其在南半球高纬度地区和全球低纬度地区.

图14 2016年全球IGS站ZTD产品验证各模型的bias和RMS在不同纬度范围内的变化Fig.14 Bias and RMS error statistics for different models tested with ZTD from IGS products in different latitude range in 2016
3 结论
针对已有对流层延迟模型的模型方程未同时顾及高程、纬度和季节变化以及模型构建使用单一格网数据等不足,提出了基于滑动窗口算法的全球ZTD模型构建新方法,最终建立了一种新的高精度全球ZTD模型(GGZTD).同时,联合未参与建模的全球GGOS大气格网ZTD产品和全球IGS站ZTD产品评估了GGZTD模型在全球的精度和适用性.结果表明:(1)以全球GGOS大气格网ZTD产品和全球IGS站精密ZTD产品为参考值,相对于UNB3m模型和GPT2w模型计算的ZTD信息,GGZTD模型在全球范围内表现出了最优的精度和稳定的性能,尤其是相对于UNB3m模型,GGZTD模型体现出了显著的精度提升,即便是相对于精度优异的GPT2w模型,其在全球的部分地区也表现出了一定的精度改善.此外,在季节、高程和纬度变化方面,GGZTD模型仍体现出了最优的性能.(2)GGZTD模型具有3240个格网点,每个格网点包含了8个模型参数.相对于GPT2w-1计算ZTD时所需的模型参数,GGZTD模型的模型参数减少了99%,而相对于GPT2w-5, 其模型参数减少了69%.因此,GGZTD模型在全球计算ZTD时只需依赖相对较少的模型参数,极大地提升了模型的计算效率,进而增强了模型在全球的适用性.总之,GGZTD模型仅需要输入位置和时间参数则能在全球获得较高精度和稳定的ZTD信息,且只依赖于相对较少的模型参数,因此其在全球坐标参考框架建立等GNSS应用和导航中具有重要的应用.由于本文在构建GGZTD模型时只考虑了固定的窗口大小和滑动步长,在下一步工作中,将采用高分辨率的ERA5资料研究不同窗口大小和步长的选取对全球ZTD建模的影响.
致谢感谢GGOS Atmosphere机构和IGS中心提供实验数据.

