一种离散时间调度的图像自分类脉冲神经网络
刘宙思,李尊朝,张剑,罗丹
(西安交通大学微电子学院,710049,西安)
脉冲神经网络(SNN)作为第3代神经网络模型[1],来源于对生物神经网络结构的模拟,是生物体神经元之间信息传递过程的抽象表述,具备充分的生物可解释性,且具有高性能和低功耗两大优势[2],在类脑计算领域特别是机器视觉方向日益成为研究焦点[3]。与传统人工神经网络相比,脉冲神经元的引入简化了连续时间编码和非线性激活的传递方式,可以有效降低实时计算的复杂度,有利于实现数据流的并行架构[4]。同时,SNN的迭代并不依赖于误差反向传播算法[5],使其对于平台算力的要求大大降低,有利于分布式系统的算法部署,能够解决边缘计算等场景下的在线学习难题[6]。因此,SNN被普遍认为是一种轻量化、高能效的硬件友好型图像识别解决方案[7-8]。
近年来,脉冲时间依赖可塑性(STDP)算法凭借其深厚的生理学基础和高效的调节性机制逐渐成为SNN模型的主流学习算法之一[8],并成功应用于现场可编程逻辑门阵列[9]和专用集成电路[10]等硬件终端上。特别地,Kheradpisheh等通过排序编码方式和简化的STDP算法进行输入特征提取,再借助支持向量机(SVM)完成输出分类,最终在Caltech数据集[11]的Face/Moto子集上取得了99.1%的准确率[12];Lee等在现有STDP算法基础上利用泊松编码和全连接的输出结构实现了SNN的自分类,对于Face/Moto数据集分类准确率可达97.6%[13]。为了进一步提高STDP算法在SNN上的分类性能,Zheng等将反向传播算法引申到STDP算法的脉冲序列模式的监督学习中,结合随机梯度下降法进行训练,并在MNIST数据集[14]上取得了97.8%的准确率[15];Mozafari等在文献[12]的基础上,通过引入强化学习来对STDP算法的权重改变量结果进行二次修正,克服了原有网络结构对SVM等外界分类器的依赖性,在Face/Moto数据集上分类准确率达到了98.9%[16]。
综上可知,研究人员在各自细分领域中针对STDP算法与SNN模型的适配工作已经做出了大量改进,但在面对实际应用场景中广泛存在的资源受限、算力瓶颈等约束问题时,仍然存在着优化空间。一方面,软件仿真若想取得更好的分类性能往往会占用更多的硬件资源,同时导致更高的计算功耗;另一方面,软件算法是神经形态计算的核心,而硬件设备是软件赖以运行的载体,二者密不可分,片面追求软件性能的背后多是对硬件算力的透支,尤其是随着面向异构计算软件平台的兴起,软硬件协同设计已经逐渐成为技术角逐的制高点之一[17]。
据此,本文参考流水线同步[18]和事件驱动[19]方案,提出了一种新型的基于离散时间调度的脉冲神经网络(DTS-SNN)模型,使得脉冲序列能够在固定时间段内依次沿网络亚层单向传播,以同步精简脉冲发放模式和传递形式。通过结合并改进经典的STDP算法和强化学习机制,优化了网络结构的适应性和稳定性,在保证网络分类性能的同时大幅降低了资源占用和模型复杂度,有利于软件算法向硬件平台的底层移植,可为高效率低功耗的小型智能化硬件终端的边缘计算方案实现提供参考。
1 网络模型
DTS-SNN模型的主体架构依托于多层前馈神经网络,以非泄漏的累积发放神经元模型[16]作为网络节点,中间突触信息采用脉冲形式传递,其基本结构如图1所示。DTS-SNN模型可分为图像输入层、滤波处理层、卷积层C1、池化层P1、卷积层C2和全局池化层P2(亦为输出层)。每当输入层在t时刻发出脉冲,脉冲将沿网络各层连续传播,最后当输出层所有通道都产生脉冲时,代表网络对单幅输入图像分类完毕。若网络处理周期为T,则此时各层中脉冲序列依次为t,t+1,t+2,…,T。其中,输入层Ⅰ完成对输入图像的编码和处理,中间层Ⅱ提取输入特征并实现高维映射,输出层Ⅲ负责输出网络对输入图像的分类结果。
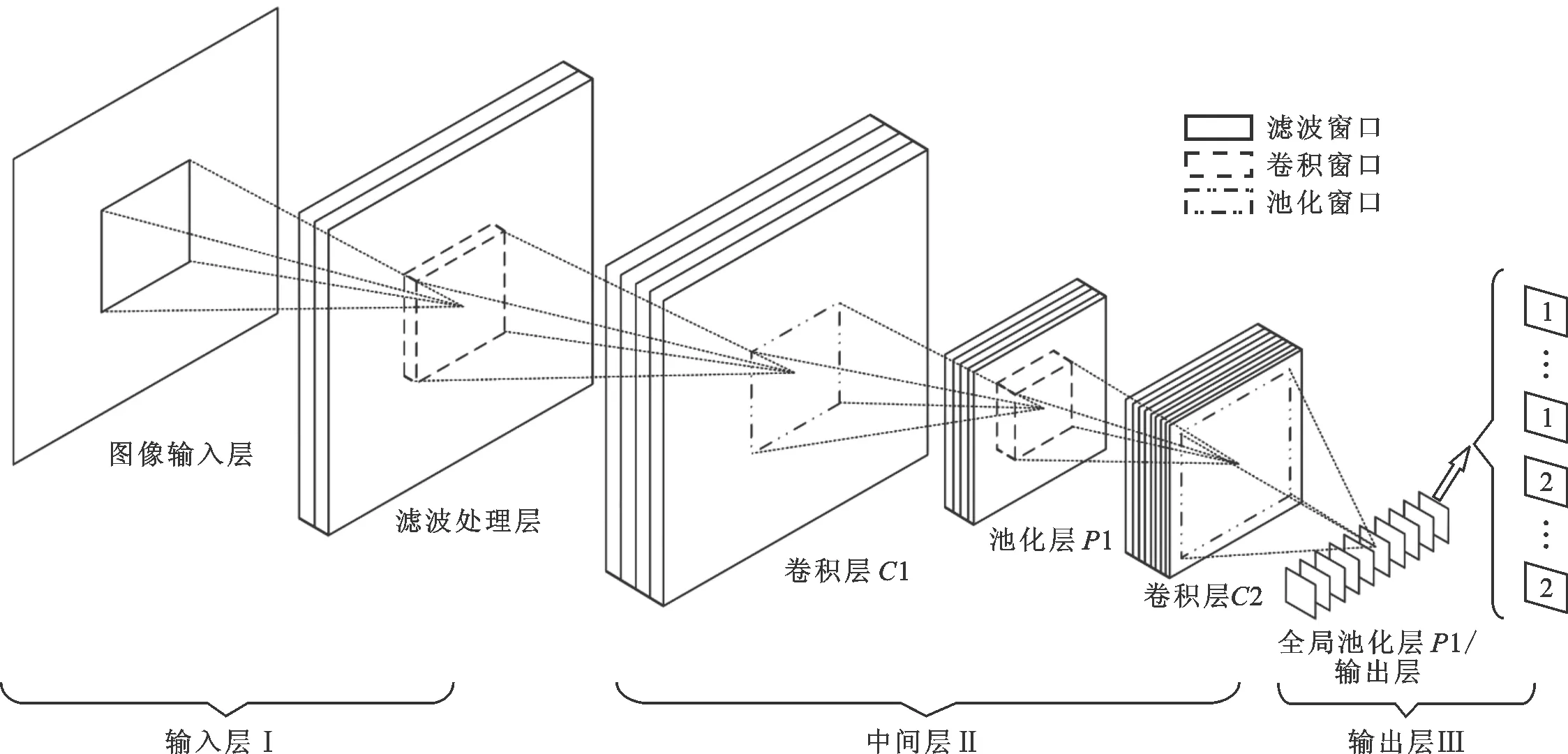
图1 DTS-SNN模型的基本结构
1.1 输入层
由于输入图像之间存在尺寸和格式上的差异,故首先需要对其进行预处理。在输入层中统一将原图像转换为大小一致的像素尺寸为250×160的灰度图像,并作去边框、阈值化处理,以减小输入层的神经元规模,同时保留图像的输入特征。
原始输入特征中通常还包含着不同程度的干扰,如多元场景、复杂光线、图像噪点等。为尽可能地凸显输入图像中的关键特征点,引入高斯差分归一化层(即滤波处理层)对原图像进行二维滤波处理。高斯核函数、差分算子和均值归一化表达式分别为
(1)
ΔG=Gσ+(x,y)-Gσ-(x,y)
(2)
(3)
式中:x和y分别为横、纵坐标参数;σ+=1;σ-=2;μ=4;ΔGmean和ΔGmax为ΔG的平均值和最大值。式中各参数取值来源于文献[12]。
网络模型的输入脉冲采用时间编码方式表示,单个神经元仅能发放单个脉冲,再经由权重连接作用于后神经元。为了将输入图像转化为输入脉冲序列,需要对各像素点的灰度值进行编码。首脉冲时间(TTFS)编码[20]是一种常用的灰度图像线性时间编码方式,像素点的灰度值越高表示输入特征越明显,相应会越早发出脉冲,灰度值越低则会越晚发出脉冲,即将灰度值0~255的像素点依次呈线性映射到T~0的时间尺度之内。为了确保所有输入层的初始脉冲都能有机会传递到输出层,初始脉冲的发放时刻应满足

(4)
式中:p为输入像素点灰度值;pmax和pmin分别为输入像素点灰度值的最大值和最小值;T为单幅输入图像的处理周期;L为网络模型层数。式(4)是向下取整离散化后的结果,符合脉冲序列的离散时间表达形式。每当某一时刻t输入层有脉冲发出,输出层至少能在t+L-1时刻产生响应,保证了输入特征在周期T内的连续传递。
图2为归一化差分算子对输入图像样例的处理过程。在排序编码方式[12]中,初始脉冲的发放时刻为对应像素点灰度值的倒数,即0~255的灰度值范围对应256种脉冲发放时刻。TTFS编码通过对灰度值进行T个周期的离散化线性编码,使其对应的脉冲编码模式缩减至排序编码的T/256,使得同组神经元在对应时刻同时产生脉冲,脉冲编码模式得以大大简化,有效提高了特征映射的并行化程度。

图2 归一化差分算子对输入图像样例的处理过程
1.2 中间层
卷积层的主要目的是通过权重共享的方式减少网络前后神经元之间的连接参数,其中C1层有利于解离,对应于输入的低维特征,C2层则倾向于重建融合后的高维特征[12]。通过对输入脉冲的多维卷积,突触后神经元可以提取到对应区域中突触前神经元阵列的组合特征。对于第j层的某一神经元φ,其在t时刻的膜电位改变量由输入神经元脉冲和突触连接参数共同决定,φ的膜电位离散表达式为
(5)
式中:θ为上一卷积层i中对应于φ的卷积窗口Ω中的输入神经元;ωij为前后神经元之间的突触连接权重;Si为θ产生的输入脉冲。所有神经元的输入脉冲形式均应满足累积发放条件[16],表达式为
(6)
当神经元的膜电位Vi未超过其阈值Vth时,神经元保持静息状态,对应Si=0;当膜电位超过阈值时,神经元转入兴奋状态,对应Si=1,且在下一时刻膜电位将复位清零。
池化层的主要目的是实现网络的数据降维和特征压缩,降低输入信息的冗余度。传统人工神经网络在配合卷积输入的前提下,可通过最大值池化的方式引入平移不变性[12],使得高维空间内的特征映射在一定程度上不受到低维空间中具体位置的影响,以达到尺度放缩的效果。在SNN中,最大值池化过程可进一步简化为脉冲池化表达式
(7)
只要池化窗口Ω内任一神经元θ在上一时刻发过脉冲,对应位置的后神经元φ即产生脉冲,对应Sj=1;当且仅当Ω内所有前神经元均未产生过脉冲时,后神经元φ保持静息状态,对应Sj=0。
针对同一层内不同通道的相同位置可能会同时产生多次脉冲的情况,在卷积和池化层均引入了侧向抑制机制。只要某一位置上的神经元率先产生了脉冲且膜电位最高,则位于相同位置处不同通道中的其他神经元均会被抑制,即同一位置上只允许发放一次脉冲,直到输入下一图像为止。这种竞争性传输机制既体现了视觉感知的生物机理,又保证了脉冲传递的单向性和稀疏性,同时还降低了网络结构的复杂程度。
1.3 输出层
输出层即为全局池化层P2,池化窗口设为整个输入卷积层C2的尺寸,统计每个通道最早产生脉冲的时刻,并作为输出神经元集群仲裁的特征向量。对于二分类任务,输出层神经元按类别标签分为两组,分别按产生脉冲的最早时刻进行投票,并统计输出结果。如果某组内神经元最早产生脉冲,则代表输入特征与该类最为相符,该神经元输出结果有效,对应该组票数增加;如果较晚时刻产生或是没有发出脉冲,则代表特征不符,该神经元输出结果无效,对应该组票数不变。当某组票数更多时,说明识别成功,输出结果即为该组标签;当两组票数相等时,说明识别失败。其中,通过在同组中设置多对一(N:1)的分类方式,可以降低输出的随机性,提高特征识别的鲁棒性和网络分类的准确率,但同时也会增加额外的训练参数,故本文中N取为5作为折中。
2 学习算法
DTS-SNN模型的训练主要针对卷积层的突触连接权重进行修改,每当新的图像输入时,所有神经元首先复位至初始状态,膜电位清零,直到学习层中某一神经元的膜电位累积达到阈值后产生首个脉冲,继而触发学习机制,使得对应位置的突触权重在原值基础上不断迭代。依据神经元的突触可塑性原理[8],网络学习以经典的STDP算法为基础,结合强化学习的奖惩机制[16],对卷积层C1和C2逐层进行训练,直至迭代完毕。由于网络采用了离散时间调度的脉冲驱动方式,因此STDP算法的连续时间窗口同样可以被降采样后的T个等距离散时刻所表示,在散列存储的结构下,其对应的空间复杂度也将大大降低。这不仅能提高相关脉冲的利用率,还能简化权重更新的计算过程,同时有利于实现硬件的并行加速。
C1层的学习过程依赖于输入图像的低维特征,与C2层相比,其卷积核尺寸小、通道少、脉冲响应阈值低,采用经典的STDP无监督学习算法可避免复杂运算,并达到输入特征分离的效果。突触权重变化量Δωij的离散表达式为
(8)
式中:Δt=ti-tj为突触前神经元脉冲和突触后神经元脉冲产生时刻的差值;a+和τ+分别为长时程增强(LTP)作用因子和时间常数;a-和τ-分别为长时程抑制(LTD)作用因子和时间常数。当Δt<0时,前神经元与后神经元之间构成因果联系,突触权重增量按照LTP过程呈指数增大,且脉冲时间相隔越短说明联系越紧密,对应突触权重增加得越多;当Δt≥0时,前后神经元之间存在逆因果联系,突触权重增量按照LTD过程呈指数减小,且脉冲时间相隔越短对应突触权重减少得越多。
C2层需要满足后续分类识别的要求,因此权重学习不仅依赖于上层输入的高维特征,还取决于输出层的类别标签[16]。本文提出采用与强化学习的奖惩机制相结合的强化STDP算法——RL-STDP,能够避免引入额外的分类器,通过将特征提取和分类输出过程融为一体来实现网络自分类,节省大量运算资源。RL-STDP算法对应的权重变化量的离散表达式为
(9)
式中各学习参数的定义与式(8)相一致,上标r和p分别对应强化学习中的奖励和惩罚机制。当输出神经元的分组标签与输入样本的真实标签一致时,触发奖励机制,对应权重按照经典STDP规则修改;当分组标签与真实标签不一致时,触发惩罚机制,对应权重按照经典STDP规则逆向修改,以修正导致预测错误的网络自适应偏差。STDP与RL-STDP算法的离散变化曲线如图3所示。

(a)STDP(b)RL-STDP图3 STDP与RL-STDP算法的离散变化曲线
在整个学习过程的时间窗口内始终未产生有效脉冲的神经元,在模型训练过程中均等同于无关项,与其连接的权重按照对应LTD作用因子(Δt=0)减小,以便清除无效连接。
与脉冲传输过程相类似,学习层中的各通道也可能在同一时刻产生多个首脉冲,故同样需要引入竞争性机制来解决多重触发的矛盾。图4是竞争性学习机制示意。竞争性学习机制按照作用域的不同可分为自抑制和互抑制两种情况,其相同点是只要学习层中的某神经元率先产生了脉冲且膜电位相对最高,就会抑制其他部分神经元的学习进程,直到输入下一图像为止。不同点是自抑制表示某神经元会对同一通道内的所有其他神经元产生抑制,即单个通道内仅由单个首脉冲神经元触发权重更新,使得同一通道内仅学习与其输入最为相符的单个特征。互抑制则表示某神经元还会对周围一定范围内不同通道中的其他神经元产生抑制,即不同通道中的特定区域内仍然仅由单个首脉冲神经元触发权重更新,使得不同通道提取各自符合的不同特征。另外,通过设置合适的权重更新次数,可以将单次学习过程中触发神经元的总数控制在一定规模内,因而对于单幅输入图像,网络至多学习到其中最具代表性的有限个特征,以此保证学习特征的唯一性和特异性。

图4 竞争性学习机制示意

(10)
LTP作用目标对应ωij的上限1,缩放因子为1-ωij;LTD作用目标对应ωij的下限0,缩放因子为ωij-0。结合式(8),可得累积后的权重∑ω表达式为
∑ω=(1+ΔωLTD)(1-ΔωLTP)ω+ΔωLTP
(11)
式中ΔωLTD和ΔωLTP分别为对应LTD和LTP过程的权重变化量。结合0<ω<1,易证0<∑ω<1。考虑到训练后期分类正确的样本数将远高于分类错误的样本数,从而反馈状态中奖励信号频次会远多于惩罚信号频次,导致模型将受限于临界极值而难以跳出固有循环,以致引发过拟合的问题,附加式(10)所示的非对称约束条件。当输出反馈惩罚信号时,LTP与LTD过程随即切换:对于保持LTP过程的奖励响应神经元,权重稳定于1附近,LTP迭代增量趋近于0,对应切换LTD后的惩罚响应增量最大;对于保持LTD过程的奖励响应神经元,权重稳定于0附近,LTD迭代增量趋近于0,对应切换LTP后的惩罚响应增量亦最大。这表明式(10)除施加边界约束外,也能充当自适应学习率[16]的调节因子,从而避免模型陷入局部最优解,以减缓过拟合。此外,为简化计算,本文将权重下限设为10-6,上限对应设为1-10-6,即在权重变化单位区间内同时附加刚性约束条件,以便精度控制和参数存取。
3 实验结果
本文将Caltech数据库中的Face/Moto类别作为数据集进行仿真实验,以验证DTS-SNN模型的有效性。每种图像类别共包含随机选取且不重复的100张图片,训练集和测试集的样本比例各占50%。实验使用CPU+GPU的多核异构PC作为测试平台,选用Anaconda3环境和Python3语言搭建仿真框架,并应用Numba库和CUDA核函数进行硬件加速。实验所使用的DTS-SNN模型的网络参数和学习参数分别如表1和表2所示,C1和C2层的训练轮次分别设为30和50,迭代次数总计为8 000。重复实验10次,取最终稳定后的测试集准确率结果的平均值作为模型的性能评价指标,同时记录训练集准确率以作参考。

表1 DTS-SNN模型的网络参数
注:窗口大小为宽度×长度×深度。

表2 DTS-SNN模型的学习参数
注:互抑制范围为宽度×长度。

(a)C2层中两个通道提取到的不同输入特征映射

(b)C1层的权重变化曲线

(c)C2层的权重变化曲线
(d)样本分类准确率的变化曲线图5 DTS-SNN模型的学习过程
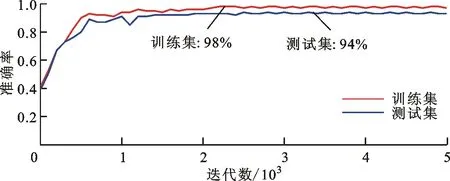
DTS-SNN模型的学习过程如图5所示,ωC1和ωC2分别为C1和C2层的权重。可以看出:随着网络模型的不断迭代,C2层的高维特征经可视化后表现得越发明显,与输入图像类别的匹配度不断增加;ωC1和ωC2的极值按照LTP和LTD过程分别收敛于1和0;模型的分类准确率由40%开始迅速上升,在迭代第6次时已能达到90%,同时对应于图6c中的C2层权重恰好近乎收敛,且在迭代20次后分类性能趋于稳定,训练集和测试集准确率分别保持在98%和94%左右,两组结果的准确率较高且差别较小,说明了模型在收敛快速且稳定的同时具有良好的泛化能力。
为了全面衡量DTS-SNN模型和学习算法的适配性,本文以现有SNN模型在Face/Moto数据集上的分类性能[13]作为对照,对不同方案在Face/Moto数据集的分类性能进行了比较,结果如表3所示。

表3 不同方案在Face/Moto数据集的分类性能比较
注:分类准确率为平均值±标准差。
由表3可知:DTS-SNN模型的测试准确率为93.4%±0.5%,相较于其他网络模型的分类准确率虽有一定程度上的降低,但权重训练参数总量仅为5×5×1×4+15×15×4×10=9 100,规模只相当于SpiCNN[13]、RL-SNN[16]、SDNN[12]的35.7%、39.4%、35.7%;在学习算法方面,RL-STDP的性能表现优于简化R-STDP[16]算法的,并解除了对SVM分类器[12]的依赖性,减少了输出分类的计算开销,具备实现图像分类的可行性和高效性。与其他方案相比,本文基于离散化时域的调度方式大大简化了脉冲转换和权重学习过程:一方面通过TTFS编码将脉冲模式限定于T=30内,相比于排序编码[12,16],压缩率达到了30/256×100%=11.7%;另一方面通过将脉冲序列间隔离散化,相比于经典的连续STDP算法[13],复杂度由O(n2)降为O(1),优化了权重更新的计算过程。同时,本文通过在网络迭代过程中引入竞争性机制,进一步保证了脉冲传递的稀疏性和学习特征的特异性,降低了网络复杂度和训练计算量。此外,双重约束条件的引入也使得模型能够在有限资源下抑制过拟合的出现,而无需借助于额外的动态学习率和随机失活[16]等方案。综上可见,本文提出的DTS-SNN模型能够在保证良好分类性能的同时有效降低模型复杂度,大幅减少资源占用率,而且结构相对独立,泛化能力较强,与其他SNN模型相比更适合于高效率、低功耗的小型智能化硬件系统的边缘计算方案实现。
在实际应用场景中,待测样本数往往多于训练样本数[12]。有鉴于此,本文通过抽样方式逐渐减少训练集样本比例,以考察DTS-SNN模型的在线学习能力。不同训练样本数下模型的实际分类性能如图6所示。可以看出:当训练样本数降为原先的60%时,测试准确率下降约8%;当训练样本数在此基础上继续减少20%时,测试准确率又降低了约6%,但仍能稳定于80%左右。随着训练样本比例减少至40%,DTS-SNN模型的分类性能确有所下降,但尚在可接受范围之内且能保持稳定,表现出较高的鲁棒性。
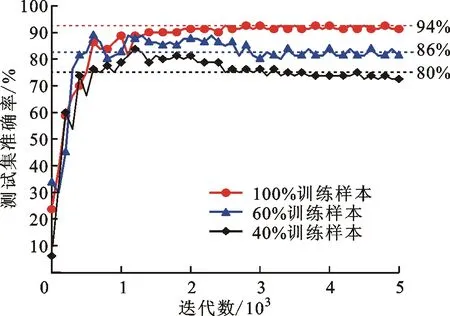
图6 不同训练样本数下模型的实际分类性能
4 结 论
为了解决现有SNN图像分类模型中存在的资源占用高和运算较复杂等实际约束问题,本文以轻量化、高能效的机器视觉优化解决方案为研究背景,提出了一种新型的基于强化STDP算法的DTS-SNN图像自分类模型,并在Face/Moto数据集上取得了良好的分类效果。
实验结果表明,与传统的SNN分类模型相比,DTS-SNN模型具有以下优势:①脉冲序列的发放和传递均采用离散时间调度方案,配合TTFS编码策略,使得脉冲模式和权重学习大为简化;②将强化学习的奖惩机制与经典STDP算法结合,实现了网络自分类,不需要借助于额外的分类器;③竞争性机制和双重约束条件的引入保证了脉冲传递的稀疏性和学习特征的特异性,有效抑制了过拟合的出现;④网络资源占用少,模型复杂程度低,且具有收敛速度快、泛化能力强、稳定性良好、鲁棒性较高等特点,有利于高效率低功耗的小型智能化硬件终端的边缘计算方案实现。

